Suppose a cluster M at a certain iteration of the k-means
algorithm contains the observations x1 = (2, 3), x2 = (−1, −3), x3
= (−2, 3). If M only cluster, what would be the sum of squared
errors
Answers
The sum of squared errors (SSE) for cluster M at that iteration would be 18.
To calculate the sum of squared errors (SSE) for a cluster M in the k-means algorithm, you need the centroid of the cluster and the squared Euclidean distance between each observation and the centroid.
Let's calculate the SSE for the given cluster M:
Observations:
x1 = (2, 3)
x2 = (-1, -3)
x3 = (-2, 3)
First, let's find the centroid of the cluster M:
Centroid = (sum of x-coordinates / number of observations, sum of y-coordinates / number of observations)
Centroid_x = (2 + (-1) + (-2)) / 3 = -1/3
Centroid_y = (3 + (-3) + 3) / 3 = 1
Centroid = (-1/3, 1)
Now, calculate the squared Euclidean distance between each observation and the centroid:
Squared Euclidean distance = (x-coordinate - centroid_x)² + (y-coordinate - centroid_y)²
For x1:
\(Distance_{x1} = (2 - (-1/3))^2 + (3 - 1)^2 \\= (7/3)^2 + 2^2 \\= 49/9 + 4\\ = 61/9\)
For x2:
\(Distance_{x2} = (-1 - (-1/3))^2 + (-3 - 1)^2\\= (-2/3)^2 + (-4)^2\\ = 4/9 + 16\\ = 52/9\)
For x3:
\(Distance_{x3} = (-2 - (-1/3))^2 + (3 - 1)^2\\ = (-5/3)^2 + 2^2 \\= 25/9 + 4\\ = 49/9\)
Now, sum up the squared distances:
SSE = Distance_x1 + Distance_x2 + Distance_x3
= 61/9 + 52/9 + 49/9
= 162/9
= 18
Therefore, the sum of squared errors (SSE) for cluster M at that iteration would be 18.
To learn more about sum of squared errors visit:
brainly.com/question/14885562
#SPJ11
Related Questions
(25 points) Find two linearly independent solutions of Y"' + 2xy = 0 of the form y1 = 1 + a3 x^3 + a6 x^6 + ... y2 = x + b4x^4 + b7x^7 + ... Enter the first few coefficients: аз = = a6 = = b4 = = by = =
Answers
The linearly independent solutions of the differential equation Y"' + 2xy = 0, in the given form, are y1 = 1 - (1/18)x⁶ + ... and y2 = x + (1/210)x⁷ + ... The coefficients a₃ = 0, a₆ = -1/18, b₄ = 0, and b₇ = 1/210.
To find two linearly independent solutions of the differential equation Y"' + 2xy = 0 in the given form, we can assume power series solutions of the form:
y1 = 1 + a₃x³ + a₆x⁶ + ...
y2 = x + b₄x⁴ + b₇x⁷ + ...
We will substitute these series into the differential equation and equate the coefficients of corresponding powers of x to find the values of the coefficients.
Substituting y1 and y2 into the differential equation, we have:
(1 + a₃x³ + a₆x⁶ + ...)''' + 2x(x + b₄x⁴ + b₇x⁷ + ...) = 0
Expanding the derivatives and collecting like terms, we can set the coefficients of corresponding powers of x to zero.
The first few coefficients are:
a₃ = 0
a₆ = -1/18
b₄ = 0
b₇ = 1/210
Therefore, the linearly independent solutions of the differential equation are
y1 = 1 - (1/18)x⁶ + ...
y2 = x + (1/210)x⁷ + ...
To know more about linearly independent solutions:
https://brainly.com/question/31849887
#SPJ4
--The given question is incomplete, the complete question is given below " (25 points) Find two linearly independent solutions of Y"' + 2xy = 0 of the form y1 = 1 + a₃ x³ + a₆ x⁶ + ...,
y2 = x + b₄x⁴ + b₇x⁷ + ...
Enter the first few coefficients: а₃=
a₆ =
b₄ =
b₇ ="--
A minor league hockey team had the following scores for the start of the season for the start of the season 3,6,2,1,2,3,0,4,5,1,5,4. What is the MODE score of the hockey team?

Answers
The given data set is:
\(3,6,2,1,2,3,0,4,5,1,5,4\)It is required to find the mode.
Recall that the mode is the value in a set of data that has the most occurrences.
Note that the mode is not unique and a data set may have no mode.
The value that has the most occurrences in the set is not unique.
Hence, the data set has no mode score
Jeff had $20. He spent 3/8
of his money on lunch. How much money does Jeff have left?
A.$12.50
B.$7.50
C.$8.25
D.$16.75
Answers
Answer:
$12.50
Step-by-step explanation:
The first one to answer gets brainy

Answers
The distance travelled in one hour is 64 miles
speed = distance / time
speed = 64 / 1
The speed is 64 miles per hour
solve the following equation 5a-4>2a+8
Answers
Answer:
4
Step-by-step explanation:
Simplifying
5a + -4 = 2a + 8
Reorder the terms:
-4 + 5a = 2a + 8
Reorder the terms:
-4 + 5a = 8 + 2a
Solving
-4 + 5a = 8 + 2a
Solving for variable 'a'.
Move all terms containing a to the left, all other terms to the right.
Add '-2a' to each side of the equation.
-4 + 5a + -2a = 8 + 2a + -2a
Combine like terms: 5a + -2a = 3a
-4 + 3a = 8 + 2a + -2a
Combine like terms: 2a + -2a = 0
-4 + 3a = 8 + 0
-4 + 3a = 8
Add '4' to each side of the equation.
-4 + 4 + 3a = 8 + 4
Combine like terms: -4 + 4 = 0
0 + 3a = 8 + 4
3a = 8 + 4
Combine like terms: 8 + 4 = 12
3a = 12
Divide each side by '3'.
a = 4
Simplifying
a = 4
The upper class is composed primarily of CEOs, government officials, celebrities, and very successful professionals. Approximately what percentage of the population does this represent
Answers
The upper class represents approximately 1-2% of the population. The upper class is composed primarily of CEOs, government officials, celebrities, and very successful professionals.
This class is the smallest among the five social classes, comprising only a tiny percentage of the population (1-2 percent).Individuals in the upper class are often referred to as the "social elite," as they are frequently born into money, live in luxurious estates, and are members of exclusive clubs. Upper-class individuals usually have excellent education and a variety of skills that have helped them accumulate wealth and power. Therefore, the upper class represents approximately 1-2% of the population.
Know more about social elite here:
https://brainly.com/question/29038983
#SPJ11
Find the least number which must be subtracted from 3255 so as to get a perfect square. PLS ANSWER I NEED IT PLS.....................
Answers
Answer:
Step-by-step explanation:
to make 3255 a perfect square subtract 6 from 3255
3255 - 6 = 3249
3249 is a perfect square
Pea aphids, Acyrthosiphon pisum, are small, wingless, sapsucking insects that live on plants. They evade predators (such as ladybugs) by dropping off. A study examined the mechanism of aphid drops. Researchers placed aphids on a leaf positioned at four different heights (in centimeters, cm) above a surface covered with petroleum jelly. When a ladybug was introduced, the aphids dropped, and the petroleum jelly helped capture their landing posture (upright or not). Each aphid performed this experiment only once. The findings are given in the table. Dropping Hcight Landing Posture3 cm 5 cm10 cm20cm Upright Not upright Sample size 20 23 10 30 30 27 29 30 30 To access the complete data set, click the link for your preferred software format: Excel Minitab JMP SPSS TI R Mac-TXT PC-TXT CSV CrunchIt! The null hypothesis "no relationship" says that in the population of aphids, the proportions that land upright are the same when the dropping height is 3, 5, 10, and 20 cm. The two-way table contains expected cell counts if this hypothesis is true Landing Posture 3 cm5 cm10 cm 20 cm Total 24.75 24.75 24.75 24.75 99 Not upright 5.255.255.255.255.25 30 30 30 30 30 Upright Total (a) Use the tables to calculate the value of the chi-square statistic. (Enter your answer rounded to three decimal places.) 223.359 Question Source Baldi4e- The Practice Of Statistics In The Life Sciences Publisher: W.H. Freeman
Answers
The value of chi-square statistic (\(X^{2}\)) is 11.26
As per the given question
the sample space of all the four cases are 30
the proportions that land upright are the same when the dropping height is 3, 5, 10, and 20 cm.
the formula of chi-squared test is
\(X^2=\sum\frac{(O_i-E_i)^2}{E}\)
where
\(X^{2}\) is chi-square
\(O_i\) is the observed value
\(E_i\) is the expected value
the upright observed value are 20,23,27,29
the upright expected values are 24.75
now
the chi-square at 3cm height is
\(X^2=\(\frac{(20-24.75)^2}{24.75}\)
=> \(X^2=0.91\)
the chi- square at 5cm height is
\(X^2=\(\frac{(23-24.75)^2}{24.75}\)
=> \(X^2=0.12\)
the value of chi-square at 10cm is
\(X^2=\(\frac{(27-24.75)^2}{24.75}\)
=>\(X^2=0.20\)
the value of chi-square at 20cm is
\(X^2=\(\frac{(29-24.75)^2}{24.75}\)
=> \(X^2=1.97\)
the not upright observed values are
10,7,3,1
the not upright expected values are 5.25
the chi-square test at 3cm height is
\(X^2=\(\frac{(10-5.25)^2}{5.25}\)
=> \(X^2=4.30\)
the chi-square test at 5cm height is
\(X^2=\(\frac{(7-5.25)^2}{5.25}\)
=> \(X^2=0.58\)
the chi-square test at 10cm height is
\(X^2=\(\frac{(3-5.25)^2}{5.25}\)
=> \(X^2=0.96\)
the chi-square test at 20 cm is
\(X^2=\(\frac{(1-5.25)^2}{5.25}\)
=> \(X^2=3.44\)
now,
the total
chi-square value at 3cm height is
=>X^2=0.91+4.30
=> \(X^{2}\)= 5.21
chi-square at 5cm height is
=> \(X^{2}=0.12+0.58\)
=> \(X^2=0.71\)
chi-square at 10cm is
=> \(X^{2}=0.20+096\)
=> \(X^2=1.16\)
chi-square at 20 cm is
=> \(X^{2}=0.73+3.44\)
=> \(X^{2}=4.17\)
now ,
the total chi-square statistic is
=>\(X^{2}=\)5.21+0.71+1.17+4.17
=>\(X^{2}=\) 11.26
To learn more about chi- square statistic:
https://brainly.com/question/28284014
#SPJ4
What is the approximate force of kinetic friction on a 50kg object sliding horizontally with a coefficient
of = 0.5
2. 5ON
b. 5OON
c. 25N
d. 250N
Answers
Answer:
F = 250 N
Step-by-step explanation:
Given that,
Mass of an object, m = 50 kg
The coefficient of kinetic friction = 0.5'
We need to find the force of kinetic friction. The kinetic friction is given by the formula as follows :
\(F=\mu N\)
N is normal force, N = mg
\(F=0.5\times 50\times 10\\\\F=250\ N\)
Hence, the force of kinetic friction is 250 N. Hence, the correct option is (d).
How many square inches of cloth are cut from the square (n = 3.14) if it’s 38inches
Answers
The number of square inches of cloth cut from the square will be 1,017.36 square inches. Then the correct option is A.
What is the area of the circle?It is the close curve of an equidistant point drawn from the center. The radius of a circle is the distance between the center and the circumference.
Let r be the radius of the circle. Then the area of the circle will be
A = πr² square units
The radius is given as,
r = 36 / 2
r = 18 inches
The area of the circle is given as,
A = π x (18)²
A = 3.14 x 324
A = 1,017.36 square inches
The number of square inches of cloth cut from the square will be 1,017.36 square inches. Then the correct option is A.
More about the area of a circle link is given below.
https://brainly.com/question/11952845
#SPJ1
The complete question is given below.
A circle is cut from a square piece of cloth, as shown:
A square, one side labeled as 36 inches, has a circle inside it. The circle touches all the sides of the square. The portion of the square outside the circle is shaded.
How many square inches of cloth is cut from the square?
(π = 3.14)
1,017.36 in2
1,489.24 in2
1,182.96 in2
1,276.00 in2
What is the value of x? What is the measure of angle 6? Show all of your work and/or explain your answer.

Answers
Answer:
1) 5 & 9
5=Corresponding Angle
9=Alternate Exterior Angle
2) 7 & 8
We know 4 is supplementary to 8. Since that is true, 7 & 8 are also.
8=Corresponing angle to 4
7=Verticle angle to 8
3) We know 1 and 3 equal 180
x-20+x+40=180
2x+20=180
2x=180-20
2x=160
x=80
<2=X+20
=80+20
=100
Angle 2 is the same as angles 5 and 6 added together.
We know angle 5 is the same as angle 1 (corresponding angles).
<1=X-20
=80-20
=60
Now that we know <2=100 and <5=60, we can figure out <6
100-60=40
<6=40°
Step-by-step explanation:
1) 5 & 9
5=Corresponding Angle
9=Alternate Exterior Angle
2) 7 & 8
We know 4 is supplementary to 8. Since that is true, 7 & 8 are also.
8=Corresponing angle to 4
7=Verticle angle to 8
3) We know 1 and 3 equal 180
x-20+x+40=180
2x+20=180
2x=180-20
2x=160
x=80
<2=X+20
=80+20
=100
Angle 2 is the same as angles 5 and 6 added together.
We know angle 5 is the same as angle 1 (corresponding angles).
<1=X-20
=80-20
=60
Now that we know <2=100 and <5=60, we can figure out <6
100-60=40
<6=40°
Easy Points!!
Question 7 of 10
Does the mapping diagram represent a function? Why or why not?
A. No; each input pairs with only one output.
B. No, the input value x = 3 pairs with two different output values.
O C. No; two output values pair with two different input values
O D. Yes; each input pairs with only one output.

Answers
Help me and explain please I’m struggling
Answers
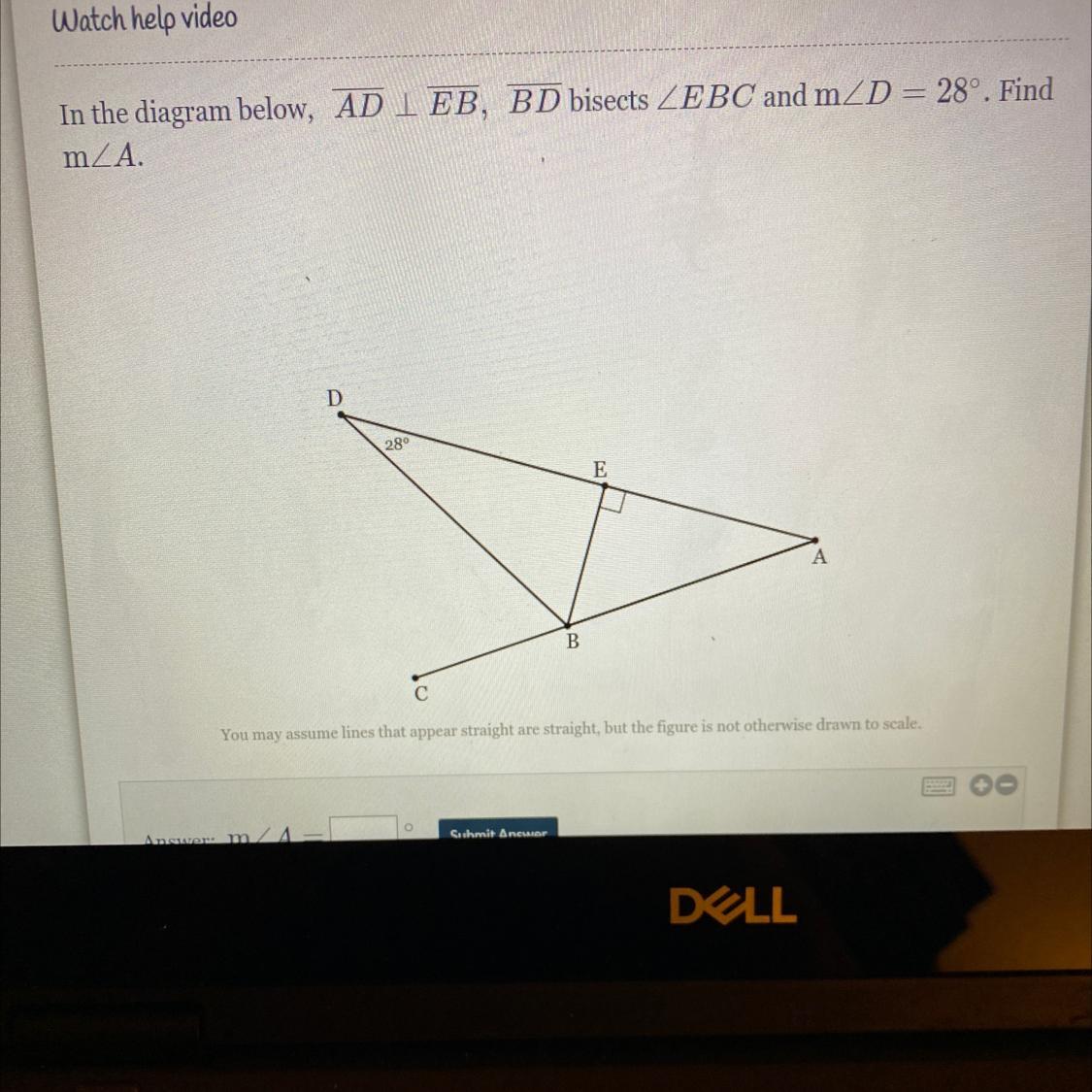
Because we know that angle AEB and BED are equal to 90°
And we know angle EBC is bisected by line BD which means the angle measures of EBD and BDC are congruent.
First we need to figure out the angles in the triangle on top, triangle EBD and we already know 2 angle measures know, 28° and 90° so we subtract those two numbers from 180 to get 62°
(The reason we subtract from 180 is because the angle measure of a triangle all together equal 180)
And based on what we said earlier (the angle measures of EBD and BDC are congruent.) the angle EBD and BDC are both equal to 62°. This means angle EBC is equal to the sum of 62 and 62, 124°. And EBC + EBA= 180° because it’s a straight angle. So to get angle EBA we subtract 124 from 180 to get 56°.
Now we can find a we just need to subtract 56 and 90 from 180, when we do that we get 34 which means that angle A is 34°
27 g^7 k^3 z^4 - 9 g^2 K^5 z
Answers
The subtraction of the expression 27 g^7 k^3 z^4 - 9 g^2 K^5 z is 18(g⁷k³z⁴ - g²k⁵z)
What are algebraic expressions?Algebraic expressions are described as expressions that are known to consist of terms, coefficients, constants, variables and factors.
They are also described as expressions composed of arithmetic operations, such as;
DivisionBracketParenthesesAdditionMultiplicationSubtractionIt is also important to note that index forms are mathematical representation of variables or values too large or small in more convenient forms.
From the information given, we have the expression;
27 g^7 k^3 z^4 - 9 g^2 K^5 z
Subtract the coefficient
18(g⁷k³z⁴ - g²k⁵z)
Hence, the value is 18(g⁷k³z⁴ - g²k⁵z)
Learn more about algebraic expressions here:
https://brainly.com/question/4344214
#SPJ1
what is 3 and 1/6 as an improper fraction
Answers
Answer:
Step-by-step explanation: 3×6+1,3×6 is 18+1 is 19/6 is your answer
15
A spinner on a board game has a radius of 3 inches and spins on a circular region as shown in the
figure.
3 in
The center of the circular region is the origin and the spinner's initial position is on the positive
x-axis. Rachel flicks the spinner, causing it to rotate 600°. What are the coordinates of the tip of
the spinner when it stops?
3
313
А
2
2
313
3
B
2
2
V3
с
1
2'
2.
V3
1
D
)
2
2

Answers
Answer:
Option A ( -3/2 , \(\frac{-3\sqrt{3} }{2}\) )
Step-by-step explanation:
According to Question, The Spinner Rotate 600* Thus after Completing 360* it Comes Exactly Where It Started . Now again rotate It 180* .Now We Are on ( -X axis ) & Completed 360*+180*=540* RotationNow After Rotate It 60* More we come in Third Quadrant & Here In Third Quadrant Only Tangent & Cotangent Is Positive .(Sine & Cosine is Negative)(For Diagram, Please Find in attachment)
Now In Triangle OAB
Cos60* = OA / OB1/2 = -X / 3 Thus X= -3/2
Sin60* = AB / OB\(\sqrt{3}\)/2 = -Y / 3 Thus Y = -\(\sqrt{3}\) * 3 /2

5. The volleyball team has a double-header on Friday. The probability that they
will win both games is 38%. The probability that they will win just the first game is
70%, What is the probability that the team will win the second game given that
they have already won the first game?
Answers
Answer: 54.29%
Step-by-step explanation:
Given: The probability that they will win both games is 38%.
i.e. P( both games will win) =0.38
The probability that they will win just the first game is 70%.
P(first game will win) = 0.70
To find : P(second game will win| first game will win)
Using formula: \(P(B|A)=\dfrac{P(\text{both A and B})}{P(A)}\)
So, P(second game will win| first game will win) = \(\dfrac{\text{ P( both games will win)}}{\text{P(first game will win)}}\)
\(=\frac{0.38}{0.70}\approx0.5429=54.29\%\)
Hence, the required probability = 54.29%
A tank of water in the shape of a cone is being filled with water at a rate of 12 m/sec. The base radius of the tank is 26 meters, and the height of the tank is 18 meters. At what rate is the depth of
Answers
The depth of the water in the cone-shaped tank is increasing at a rate of approximately 1.385 meters per second.
To determine the rate at which the depth of the water is changing, we can use related rates. Let's denote the depth of the water as h(t), where t represents time. We are given that dh/dt (the rate of change of h with respect to time) is 12 m/sec, and we want to find dh/dt when h = 18 meters.
To solve this problem, we can use the volume formula for a cone, which is V = (1/3)πr^2h, where r is the base radius and h is the depth of the water. We can differentiate this equation with respect to time t, keeping in mind that r is a constant (since the base radius does not change).
By differentiating the volume formula with respect to t, we get dV/dt = (1/3)πr^2(dh/dt). Now we can substitute the given values: dV/dt = 12 m/sec, r = 26 meters, and h = 18 meters.
Solving for dh/dt, we have (1/3)π(26^2) (dh/dt) = 12 m/sec. Rearranging this equation and solving for dh/dt, we find that dh/dt is approximately 1.385 meters per second. Therefore, the depth of the water in the tank is increasing at a rate of about 1.385 meters per second.
Learn more about volume of cone here: brainly.com/question/16419032
#SPJ11
Base salary is 100 percent, added bonus is 6 percent, total salary is 106 percent.
Use the diagram to help you solve the problem.
Mark is a receptionist for Exclusive Auto Sales. His base salary is $21,000. He has a good year of customer service, so the company also gives him a 6 percent year-end bonus based on his salary. How much does Mark make, including his base salary and the year-end bonus?
Answers
Answer:
22,260
Step-by-step explanation:
Answer:
i just took the answer thing and it would be 22,260 sorry i am so late with the answer but yea hope this helps
what two positive real numbers whose product is 11 have the smallest possible sum?
Answers
The two positive real numbers with a product of 11 that have the smallest possible sum are √11 and √11. In decimal form, these numbers are approximately 3.3166 and 3.3166.
To determine two positive real numbers whose product is 11 and have the smallest possible sum, we can use the concept of the arithmetic mean-geometric mean inequality.
Let the two numbers be x and y.
We have the following conditions:
1. xy = 11 (product of the two numbers is 11)
2. x > 0, y > 0 (both numbers are positive)
According to the AM-GM inequality, the arithmetic mean of two numbers is always greater than or equal to the geometric mean of those numbers.
Using this inequality, we have:
(x + y)/2 ≥ √(xy)
Substituting the value of xy as 11, we get:
(x + y)/2 ≥ √11
To minimize the sum (x + y), we need to make it as close as possible to the right side of the inequality.
This occurs when equality holds, that is, when:
x = y = √11
So, the answer is approximately (3.3166, 3.3166).
To know more about arithmetic mean-geometric mean refer here:
https://brainly.com/question/28145873#
#SPJ11
cho hàm số y=f[x] có bảng biến thiên
Answers
Answer:
6fc5dx7 8tfl 8tf . 8tfl 8tf tfd4 4 Ltd Ltd PM. tfl t
please help i don't understand

Answers
Each piece of furniture used 4/25 gallons of paint. The answer lies between 0 and 1, and each piece of furniture used 0.16 gallons of paint.
A mixed number is what?A full number plus a legal fraction are combined to form a mixed number. It is expressed in the form of "a b/c", where "a" is the whole number, "b" is the constant term of the correct fraction, and "c" is the denominator of the proper fraction. For instance, the mixed number 3 1/4, which equals three and one-fourth, is a mixed number. The entire integer can also be expressed as an improper fraction by multiplying it by the fraction's denominator, adding the numerator, and then putting the resulting sum over the denominator.
Let us suppose the amount of paint used = x.
Thus,
20x + 5x = 4
25x = 4
x = 4/25
Therefore, each piece of furniture used 4/25 gallons of paint.
To find between what two whole numbers the answer lies, we can convert 4/25 to a mixed number:
4/25 = 0.16
Hence, the answer lies between 0 and 1, and each piece of furniture used 0.16 gallons of paint.
Learn more about mixed numbers here:
https://brainly.com/question/24137171
#SPJ1
You need to change a blown outdoor lightbulb on your house. The bulb is 27ft up, but you have a 3ft reach from the top of the ladder. If you need the base of the ladder 7ft off the house for stability, what is the minimum height of the ladder in feet?
Answers
The minimum height of the ladder needed to change the lightbulb is 29 feet.
To determine the minimum height of the ladder, we need to use the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides.
In this problem, the ladder acts as the hypotenuse of a right triangle, and we know the height of the lightbulb (27 feet), the reach of the ladder (3 feet), and the distance between the ladder and the wall of the house (7 feet).
Let h be the minimum height of the ladder. Then, using the Pythagorean theorem, we have:
h^2 = 27^2 + 7^2 + 3^2
h^2 = 729 + 49 + 9
h^2 = 787
h ≈ 28.06
Since we need to round up to the nearest whole number (since ladders come in discrete sizes), the minimum height of the ladder needed is 29 feet.
Learn more about lightbulb here
https://brainly.com/question/14124370
#SPJ11
In a bird park 21 out of 175 birds are flamingos.what percentage of birds are flamingos in the bird park.
Answers
Answer:
12 %Step-by-step explanation:
Covert 21 out of 175 into percentage:
21/175*100% = 12 %We need percentage
\(\\ \bull\sf\dashrightarrow \dfrac{21}{175}\times 100\)
\(\\ \bull\sf\dashrightarrow \dfrac{21}{7}\times 4\)
\(\\ \bull\sf\dashrightarrow 3(4)\)
\(\\ \bull\sf\dashrightarrow 12\%\)
let the cp be rs x. if a man gains 20% profit by selling an article for rs 816. find cp
Answers
Answer:
Let, the c.p be x.
Given,
profit % = 20%
S.P = rs 816
c.p = x
We know,
profit = p% of c.p
= \(\frac{20}{100}\) * x
= \(\frac{x}{5}\)
now,
C.p = profit + s.p.
x = \(\frac{x}{5}\) + 816
x = \(\frac{x+ 4080}{5}\)
5x = x + 4080
5x-x = 4080
4x = 4080
x = \(\frac{4080}{4}\)
x = Rs 1080
Hence, the c.p is Rs. 1080
Write an equation in slope-intercept form for the line that passes through the given point and is parallel to the following equation. Point: (5,4) Equation: y = 2/5x - 2
Answers
Answer:
y = (2/5)x + 2
Step-by-step explanation:
The given equation y = (2/5)x - 2 is already in slope-intercept form. The equation of the new line has precisely that form, except that the constant is different. To find the new constant (which is the y-intercept), replace x with 5 and y with 4 in y = (2/5)x + C:
4 = (2/5)(5) + C, or
4 = 2 + C. Therefore, C = 2 and the equation of the new line is y = (2/5)x + 2.
write each equation in vertex form. then identify the vertex, axis of symmetry and direction of opening. y=x^2+8x+\:18 , y=-\:x^2\:\:12x\:-\:36 and y=2x^2\:+\:12x\:+\:13
Answers
The equation in vertex form is y = 2(x+3)² + 1. The vertex is (-3,1), the axis of symmetry is x = -3, and the direction of opening is upwards.
The vertex form of the equation is y = a(x-h)^2 + k, where (h, k) is the vertex. The axis of symmetry is x = h, and the direction of opening is determined by the value of a.
Using this formula, let us write each equation in vertex form and then identify the vertex, axis of symmetry, and direction of opening.
1. y = x² + 8x + 18
To write this equation in vertex form, we need to complete the square. y = x² + 8x + 18 is equivalent to y = (x+4)² - 2. Therefore, the equation in vertex form is y = (x+4)² - 2.
The vertex is (-4,-2), the axis of symmetry is x = -4, and the direction of opening is upwards.2
. y = -x² - 12x - 36To write this equation in vertex form, we need to complete the square. y = -x² - 12x - 36 is equivalent to y = -(x+6)² - 12. Therefore, the equation in vertex form is y = -(x+6)² - 12.
The vertex is (-6,-12), the axis of symmetry is x = -6, and the direction of opening is downwards.3. y = 2x² + 12x + 13To write this equation in vertex form, we need to complete the square. y = 2x² + 12x + 13 is equivalent to y = 2(x+3)² + 1.
To learn more about : vertex form
https://brainly.com/question/31546205
#SPJ8
n a bolt factory, machines a, b, and c manufacture 25%, 35%, and 40% of the total of their output, respectively. out of them, 5%, 4%, and 2% are defective bolts. a bolt is drawn at random from the product and is found to be defective. what are the probabilities that it was manufactured by machines a, b, and c?
Answers
The probabilities that the defective bolt was manufactured by machines A, B, and C are approximately 0.3623, 0.4058, and 0.2319, respectively.
To solve this problem, we can use Bayes' theorem.
Let's denote the events as follows:
A: Bolt is manufactured by machine A
B: Bolt is manufactured by machine B
C: Bolt is manufactured by machine C
D: Bolt is defective
We need to find the conditional probabilities P(A|D), P(B|D), and P(C|D). According to Bayes' theorem:
P(A|D) = (P(D|A) x P(A)) / P(D)
P(B|D) = (P(D|B) x P(B)) / P(D)
P(C|D) = (P(D|C) x P(C)) / P(D)
We are given the following information:
P(A) = 0.25 (machine A manufactures 25% of the total output)
P(B) = 0.35 (machine B manufactures 35% of the total output)
P(C) = 0.40 (machine C manufactures 40% of the total output)
P(D|A) = 0.05 (5% of machine A's output is defective)
P(D|B) = 0.04 (4% of machine B's output is defective)
P(D|C) = 0.02 (2% of machine C's output is defective)
To calculate P(D), we can use the law of total probability:
P(D) = P(D|A) x P(A) + P(D|B) x P(B) + P(D|C) x P(C)
Let's substitute the given values into the equations:
P(D) = (0.05 x 0.25) + (0.04 x 0.35) + (0.02 x 0.40)
= 0.0125 + 0.014 + 0.008
= 0.0345
Now, we can calculate the conditional probabilities:
P(A|D) = (0.05 x 0.25) / 0.0345
= 0.0125 / 0.0345
≈ 0.3623
P(B|D) = (0.04 x 0.35) / 0.0345
= 0.014 / 0.0345
≈ 0.4058
P(C|D) = (0.02 x 0.40) / 0.0345
= 0.008 / 0.0345
≈ 0.2319
Therefore, the probabilities that the defective bolt was manufactured by machines A, B, and C are approximately 0.3623, 0.4058, and 0.2319, respectively.
Learn more about conditional probability click;
https://brainly.com/question/11899923
#SPJ4
Determine the value of x in the triangle shown.
Question 3 options:
132°
228°
42°
48°

Answers
Answer:
x = 132°
Just add the opposite interior angles
30 points Solve for m m/6+9=12
Answers
Answer:
M = 18
Step-by-step explanation: