Suppose a sample of 400 participants was randomly selected from the middle schools and high schools in a large city. These participants responded to the question:
Which type of movie do you prefer to watch?
160 participants preferred action movies.
80 participants preferred drama movies.
40 participants preferred science-fiction movies.
240 participants were females.
78 female participants preferred drama movies.
32 male participants preferred science-fiction movies.
60 female participants preferred action movies.

Answers
Answer:
8 (a=8)
Step-by-step explanation:
40-32 = 8
Related Questions
6: A wooden rod is 4/5m
long .
Find the total length of 4 wooden rods.
Answers
Answer:
Proper: 3 and 1/5 Improper: 16/5
Step-by-step explanation:
4 times 4/5 = 16/5
5*3=15
16-15= 1
3 and 1/5
The ordering and transportation cost €C for components used in manufacturing process is approximated by the function below, where C is measured in thousands of dollars and is the order size in hundreds_ C(x) = s(x x+3 (a) Verify that C(3) C(6) _ c(3) (b) According to Rolle's Theorem, the rate of change of the cost must be for some order size in the interval (3 answer to the nearest whole number:) components Find that order size (Round vour Need Help? Ialkto Tutor
Answers
The value of x in the interval (3 < x < 6) for which the rate of change of the cost is zero.
(a) To verify that C(3) < C(6), we have to find the values of C(3) and C(6).The given function is C(x) = s(x x+3)The order size is measured in hundreds. So, when x = 3, the order size is 300 and when x = 6, the order size is 600.Therefore, C(3) = s(3 x 3+3) = s(18) and C(6) = s(6 x 6+3) = s(39)Now, as s(x) > 0, we can see that C(6) > C(3). Hence, C(3) < C(6).(b) According to Rolle's Theorem, the rate of change of the cost must be 0 for some order size in the interval (3 < x < 6).We know that the function is continuous and differentiable in the interval (3 < x < 6). Now, the rate of change of the cost is given by the derivative of the function C(x) with respect to x.C(x) = s(x x+3)C'(x) = s[1 + (x + 3) . 1] = s(1 + x + 3) = s(x + 4)As per Rolle's Theorem, there must exist a value of x in the interval (3 < x < 6) such that C'(x) = 0.So, s(x + 4) = 0x + 4 = 0x = -4Thus, the order size is -4 x 100 = -400. However, this is an absurd answer as the order size cannot be negative. Therefore, there is no value of x in the interval (3 < x < 6) for which the rate of change of the cost is zero.
Learn more about Interval
brainly.com/question/4184136
#SPJ11
Triangle A has a height of 2.5\text{ cm}2.5 cm2, point, 5, start text, space, c, m, end text and a base of 1.6\text{ cm}1.6 cm1, point, 6, start text, space, c, m, end text. The height and base of triangle B are proportional to the height and base of triangle A.
Which of the following could be the height and base of triangle B?
Choose 3 answers:
Choose 3 answers:
(Choice A) Height: 2.75\text{ cm}2.75 cm2, point, 75, start text, space, c, m, end text
Base: 1.76\text{ cm}1.76 cm1, point, 76, start text, space, c, m, end text
A
Height: 2.75\text{ cm}2.75 cm2, point, 75, start text, space, c, m, end text
Base: 1.76\text{ cm}1.76 cm1, point, 76, start text, space, c, m, end text
(Choice B) Height: 9.25\text{ cm}9.25 cm9, point, 25, start text, space, c, m, end text
Base: 9.16\text{ cm}9.16 cm9, point, 16, start text, space, c, m, end text
B
Height: 9.25\text{ cm}9.25 cm9, point, 25, start text, space, c, m, end text
Base: 9.16\text{ cm}9.16 cm9, point, 16, start text, space, c, m, end text
(Choice C) Height: 3.2\text{ cm}3.2 cm3, point, 2, start text, space, c, m, end text
Base: 5\text{ cm}5 cm5, start text, space, c, m, end text
C
Height: 3.2\text{ cm}3.2 cm3, point, 2, start text, space, c, m, end text
Base: 5\text{ cm}5 cm5, start text, space, c, m, end text
(Choice D) Height: 1.25\text{ cm}1.25 cm1, point, 25, start text, space, c, m, end text
Base: 0.8\text{ cm}0.8 cm0, point, 8, start text, space, c, m, end text
D
Height: 1.25\text{ cm}1.25 cm1, point, 25, start text, space, c, m, end text
Base: 0.8\text{ cm}0.8 cm0, point, 8, start text, space, c, m, end text
(Choice E) Height: 2\text{ cm}2 cm2, start text, space, c, m, end text
Base: 1.28\text{ cm}1.28 cm1, point, 28, start text, space, c, m, end text
E
Height: 2\text{ cm}2 cm2, start text, space, c, m, end text
Base: 1.28\text{ cm}1.28 cm
Answers
The correct options regarding the triangle will be:
A)Height: 2.75 CM
Base: 1.76 CM
D)Height: 1.25 cm
Base:0.8 cm
E) height: 2 cm
base: 1.28 cm
How to explain the valueWe know that if the height and base of triangle B are proportional to the height and base of triangle A, then their ratios of the height to the base must be equal
We need to find out the ratio of the height to the base of triangle A
= 2.75 / 1.75= 1.5
D)Height: 1.25 cm
Base:0.8 cm
= 1.25 / 0.8
= 1.56
E) height: 2 cm
base: 1.28 cm
This also gives 1.56
The correct options are A D and E.
Learn more about triangles on
https://brainly.com/question/13750574
#SPJ1
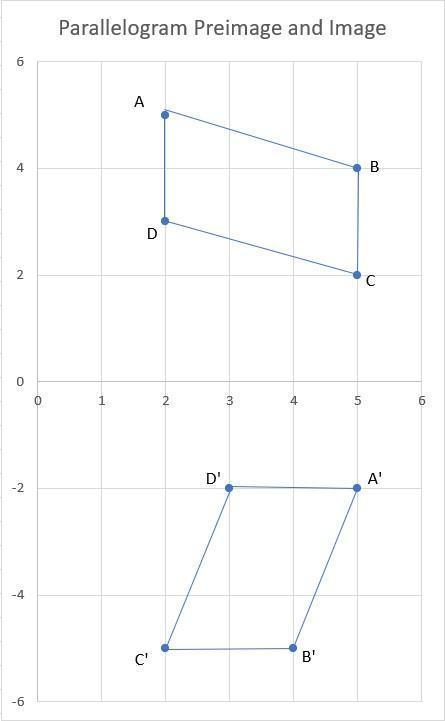
Parallelogram ABCD is rotated to create image A'B'C'D'.
Answers
The transformation rule that describes the rotation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
The rule that describes the transformation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
To understand this, let's apply the transformation rule to each vertex of the original parallelogram ABCD:
Point A (2, 5) becomes A' (-5, 2).
Point B (5, 4) becomes B' (-4, 5).
Point C (5, 2) becomes C' (-2, 5).
Point D (2, 3) becomes D' (-3, 2).
By applying the transformation rule, we observe that the x-coordinate of each point becomes the negative of the original y-coordinate, and the y-coordinate becomes the original x-coordinate.
This transformation is a 90-degree counterclockwise rotation about the origin (0, 0) on the coordinate plane. The image parallelogram A'B'C'D' is obtained by rotating the original parallelogram ABCD by 90 degrees counterclockwise.
Visually, this transformation can be seen as the original parallelogram being rotated around the origin, where the x-axis becomes the y-axis, and the y-axis becomes the negative x-axis.
Therefore, the transformation rule that describes the rotation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
For more such questions on parallelogram visit:
https://brainly.com/question/970600
#SPJ8
Mr. Jubran goes to a restaurant and has a bill of $32.57. He uses a 10% off coupon
on the cost of the meal. The tax is 8%. He leaves a tip of 18% on the amount
before the coupon or tax applied. How much does he spend?
Answers
Answer:
$36.97
The cost of the meal was $32.57 and he used a 10% off coupon. You can make 10% equal to 0.1 because . Now do . This is the discount, so you want to subtract this from the original to get the actual price of the meal, .
The tax was 8% so this means he is adding
GIVING BRAINLIEST ONCE AGAIN

Answers
Answer:
45
Step-by-step explanation:
divide 25 by 5 to see how they got that, which is 5. then multiply 9 by 5 bc you have to do the same thing, which is 45.
Answer:
5:9 = 25:45
Step-by-step explanation:
In a research study conducted to determine if arrests were related to the socioeconomic class of the offender, the chi square critical score was 9.488 and the chi square test statistic was 12.2. We can conclude that
Answers
We can conclude that the socioeconomic class of the offender is related to the likelihood of arrests.
Based on the information provided, we can conclude that there is a significant relationship between arrests and the socioeconomic class of the offender.
Identify the chi-square critical score: 9.488
Identify the chi-square test statistic: 12.2
Compare the test statistic to the critical score:
If the test statistic (12.2) is greater than the critical score (9.488), then there is a significant relationship between the variables.
In this case, 12.2 > 9.488, so there is a significant relationship between arrests and the socioeconomic class of the offender.
For similar question on socioeconomic.
https://brainly.com/question/31093929
#SPJ11
A 6.50 percent coupon bond with 18 years left to maturity is offered for sale at $1,035.25. What yield to maturity [interest rate] is the bond offering? Assume interest payments are paid semi-annually, and solve using semi-annual compounding. Par value is $1000. 3. You have just paid $1,135.90 for a bond, which has 10 years before it, matures. It pays interest every six months. If you require an 8 percent return from this bond, what is the coupon rate on this bond? Par value is $1000. [Annual Compounding Answer] [Answer here] [Semi-annual Compounding Answer] 2. A 6.50 percent coupon bond with 18 years left to maturity is offered for sale at $1,035.25. What yield to maturity [interest rate] is the bond offering? Assume interest payments are paid semi-annually, and solve using semi-annual compounding. Par value is $1000. 3. You have just paid $1,135.90 for a bond, which has 10 years. before it, matures. It pays interest every months. If you require an 8 percent return from this bond, what is the coupon rate on this bond? Par value is $1000. [Annual Compounding Answer] [Answer here] [Semi-annual Compounding Answer]
Answers
In the first scenario, a 6.50 percent coupon bond with 18 years left to maturity is priced at $1,035.25. We need to calculate the yield to maturity (interest rate) for this bond, assuming semi-annual compounding.
Scenario 1: To find the yield to maturity for the 6.50 percent coupon bond, we can use the present value formula for bond pricing. The formula is: \(Price = C * [1 - (1 + r)^{(-n)}] / r + F / (1 + r)^n\), where C is the coupon payment, r is the yield to maturity (interest rate), n is the number of periods, and F is the par value. Plugging in the given values, we have \($1,035.25 = (6.50/2) * [1 - (1 + r/2)^{(-182)}] / (r/2) + 1000 / (1 + r/2)^{(182)}\). Solving this equation for r will give us the yield to maturity.
Scenario 2: To find the coupon rate for the bond purchased at $1,135.90, we can again use the present value formula, but this time we need to solve for C. Rearranging the formula, we have \(C = (r * F) / (1 - (1 + r)^{(-n)})\), where C is the coupon payment, r is the required return (interest rate), F is the par value, and n is the number of periods.
Plugging in the given values, we have \(C = (0.08 * 1000) / (1 - (1 + 0.08)^{(-10*2)})\). Solving this equation for C will give us the coupon rate.
By solving the equations in both scenarios using the appropriate compounding periods, we can find the answers for the coupon rate and the yield to maturity.
Learn more about compounding here:
https://brainly.com/question/3433240
#SPJ11
use the net to find the surface area of the prism
a. 268 m2
b. 402.62 m2
c. 725.32 m2
d. 853 m2
please hurry

Answers
Answer:
b. 402.62 m²
Step-by-step explanation:
The area of two triangles = 2(4×6/2) = 24 m²
The area of the 1st rectangle = 6 × 22 = 132 m²
The area of the 2nd rectangle = 7.21 × 22 = 158.62 m²
The area of the 3rd rectangle = 4 × 22 = 88 m²
Total = 24 + 132 + 158.62 + 88 = 402.62 m²
What is the area of the square
One side has 5 feet
A)10 square feet
B) 25 square feet
C) 20 square feet
D) 5 square feet
Answers
There are 30 students in a class. 10 students have a pet dog, 13 students have a pet cat, and 7 students have a pet fish. 4 students have both a pet dog and a pet cat, 6 students have a pet cat and a pet fish, 2 students have a pet dog and a pet fish. 1 student has all three. How many of the 30 students have pets?
Answers
Answer:
9 students have pets
Step-by-step explanation:
From the above question, we are given the following information
Total number of students = 30
Let Pet Dog = D
Pet Cat = C
Pet Fish = F
Number is students that have pet dog
(D) = 10 students
Number of students that have pet cat (C) = 13 students
Number of students that have pet fish (F) = 7 students
Number of students that have Pet dog and cat ( D and C) = 4 students
Number of students that have Pet cat and fish (C and F) = 6 students
Number of student that has pet dog and pet fish (D and F) = 2 students
1 student has all three = ( D and F and C)
Number of student that have a pet Dog only
= n(D) - [n( D and C) + n( D and F) - n(D and C and F)]
= 10 -( 4+ 2 -1)
= 10 - 5
= 5
Number of student that have Pet cat only
= n(C) -[ n( D and C) + n( C and F) - n( D and C and F)]
= 13 -( 4 + 6 - 1)
= 13 - 9
= 4
Number is student that have a pet fish only
= n(F) - [n (C and F) + n( D and F) - n( D and C and F)]
= 7 - [6 + 2 - 1]
= 7 - 7
= 0
The number of students that have pets is calculated as:
(Number of students that have dogs only + Number of student that have cats only + Number of students that have fish only)
= 5 + 4 + 0
= 9
Therefore only 9 students have pets.
Find the number of all the 2-digit numbers satisfying the
following congruences x = 3(mod7), x = 2(mod5).
OLEASE HELP
Answers
Use the Chinese remainder theorem.
Start with x = 3×5 + 2×7 = 15 + 14 = 29. Now,
• 29 ≡ 15 ≡ 1 (mod7)
• 29 ≡ 14 ≡ 4 (mod5)
Adjust for this by multiplying the first term in x by 3, and the second term by 3 (because 4×3 ≡ 12 ≡ 2 (mod5)).
So now x = 3×5×3 + 2×7×3 = 45 + 42 = 87, and
• 87 ≡ 45 ≡ 3 (mod7)
• 87 ≡ 42 ≡ 2 (mod5)
The CRT then says that x ≡ 87 (mod(7×5)) ≡ 87 (mod35), which is to say any number x = 87 + 35n satisfies both congruences (where n is any integer).
So there are 3 possible 2-digit numbers that work: {17, 52, 87}.
To confirm:
• 17 ≡ 15 + 2 ≡ 2 (mod5) and 17 ≡ 14 + 3 ≡ 3 (mod7)
• 52 ≡ 50 + 2 ≡ 2 (mod5) and 52 ≡ 49 + 3 ≡ 3 (mod7)
• 87 ≡ 85 + 2 ≡ 2 (mod5) and 87 ≡ 84 + 3 ≡ 3 (mod7)
Solve the system by substitution. 5x+2y=5 y=(-2x+3
Answers
Answer:
(x, y) = (-1, 5)
Step-by-step explanation:
You want to solve this system of equations by substitution.
5x +2y = 5y = -2x +3SubstitutionThe idea of substitution means we want to replace an expression in one equation for an equivalent expression based on the other equation.
Here, the second equation gives an expression equivalent to "y", so we can use that expression in place of y in the first equation:
5x +2(-2x +3) = 5 . . . . . . . . (-2x+3) substitutes for y
x +6 = 5 . . . . . . . . . . simplify
x = -1 . . . . . . . . . subtract 6
y = -2(-1) +3 = 5 . . . . . use the second equation to find y
The solution is (x, y) = (-1, 5).
__
Additional comment
Choosing substitution as the solution method often works well if one of the equations gives an expression for one of the variables, or if it can be solved easily for one of the variables. The "y=" equation is a good candidate for providing an expression that can be substituted for y.
Any equation that has one of the variables with a coefficient of +1 or -1 is also a good candidate for providing a substitution expression.
4x -y = 3 ⇒ y = 4x -3 . . . . . for example
The attached graph confirms the solution above.

pls, help (20 points) All of the following equations have the same solution except _____.

Answers
All of the aforementioned equations have the same solution except: C. y/3 - 5 = -5.
What is zero solution?In Mathematics, an equation is said to have zero solution or no solution when the left hand side and right hand side of the equation are not the same or equal when simplified.
This ultimately implies that, an equation would have zero solution or no solution when both sides of the equal sign are not the same and the variables cancel out when simplified.
How to determine the solution to this equation?From the information provided, we have the following equation:
y/-1 - 6 = -5
Adding 6 to both sides of the equation, we have:
y/-1 - 6 + 6 = -5 + 6
y/-1 = -1
Multiplying both sides of the equation, we have:
-1 × (y/-1) = 1 × -1
y = -1.
-y + 4 = 5
Rearranging the equation by collecting like terms, we have:
y = 4 -5
y = -1
y/3 - 5 = -5
Adding 5 to both sides of the equation, we have:
y/3 - 5 + 5 = -5 + 5
y/3 = 0
y = 0 (different solution).
2y - 5 = -7
Adding 5 to both sides of the equation, we have:
2y - 5 + 5 = -7 + 5
2y = -2
Dividing both sides of the equation by 2, we have:
y = -2/2
y = -1.
Read more on equation here: brainly.com/question/28949611
#SPJ1
Which angle is formed by EA−→
and EG−→−?
Select all that apply.

Answers
Answer:
Step-by-step explanation:
\(\angle 2,\angle AEG, \angle GEB\)
A piece of paper is LaTeX: 8\frac{1}{2}8 1 2 inches wide. You tape 7 pieces of paper together to make a banner. How long is your banner? Type your answer as a simplified fraction using the forward slash "/".
Answers
Answer:
81/2
Step-by-step explanation:
you need to divid that o getter
A class has six students. What is the probability that exactly four of the students were born on a weekend?
Answers
ANSWER
\(P\text{ = }\frac{400}{823543}\)EXPLANATION
There are six students in the class.
There are 7 days in a week. There are 2 days in the weekend. There are 5 weekdays.
The probability that any student is born on the weekend is given as:
P(weekend) = 2/7
The probability of being born on a weekday is:
P(weekday) = 5/7
Now the probability that 4 out of the six students is born on a weekend will be given as the products of four of them born on a weekend and the remaining two born on a week day:
\(\begin{gathered} P(4\text{ are born on a weekend) = }\frac{2}{7}\cdot\text{ }\frac{2}{7}\cdot\text{ }\frac{2}{7}\cdot\text{ }\frac{2}{7}\cdot\text{ }\frac{5}{7}\cdot\text{ }\frac{5}{7} \\ P\text{ = }\frac{400}{823543} \end{gathered}\)That is the probability that 4 out of 6 of them are born on a weekend.
Point M is the midpoint of line segment CD,
shown below.
What are the coordinates of point M?
C (6,10)
M
D (20, 18)
Answers
Answer:
M(13, 14)-------------------------
Each coordinate of the midpoint is the average of endpoints:
x = (6 + 20)/2 = 26/2 = 13y = (10 + 18)/2 = 28/2 = 14Therefore M is (13, 14).
Solve the following matrix system:
The explanation how you did it would help! Thanks in advance!

Answers
Answer:
See below
Step-by-step explanation:
\(X - Y = \begin{pmatrix} 1 & 2 & 7 \\ - 1 & 3 & 5 \\ 3 & 1 & 7 \end{pmatrix} \\\\ X + Y = \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 3 \\ - 1 & 3 & 3 \end{pmatrix} \\ adding \: both \: the \: matrices \\ \\ X - Y + X + Y \\ = \begin{pmatrix} 1 & 2 & 7 \\ - 1 & 3 & 5 \\ 3 & 1 & 7 \end{pmatrix} + \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 3 \\ - 1 & 3 & 3 \end{pmatrix} \\\\ 2X= \begin{pmatrix} 1 + 1 & 2 + 0 & 7 + 1 \\ - 1 + 1 & 3 + 1 & 5 + 3\\ 3 - 1 & 1 + 3 & 7 + 3 \end{pmatrix} \\ \\ 2X= \begin{pmatrix} 2 & 2 & 8 \\ 0 & 4 & 8\\ 2 & 4 & 10 \end{pmatrix} \\ \\ X= \frac{1}{2} \begin{pmatrix} 2 & 2 & 8 \\ 0 & 4 & 8\\ 2 & 4 & 10 \end{pmatrix}\\ \\ X= \huge\begin{pmatrix} \frac{2}{2} & \frac{2}{2} & \frac{8}{2} \\ \\ \frac{0}{2} & \frac{4}{2} & \frac{8}{2}\\ \\ \frac{2}{2} & \frac{4}{2} & \frac{10}{2} \end{pmatrix} \\ \\ \huge \red{X= \begin{pmatrix} 1 & 1 & 4\\ \\ 0 & 2 & 4\\ \\ 1 & 2& 5 \end{pmatrix}} \\ \\ subtracting \: the \: value \: of \: x \: from \: matrix \: (2) \\ \\ X + Y - X \\ = \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 3 \\ - 1 & 3 & 3 \end{pmatrix} - \begin{pmatrix} 1 & 1 & 4 \\ 0 & 2 & 4\\ 1 & 2& 5 \end{pmatrix} \\ \\ Y = \begin{pmatrix} 1 - 1 & 0 - 1 & 1 - 4 \\ 1 - 0& 1 - 2 & 3 - 4 \\ - 1 - 1 & 3 - 2 & 3 - 5 \end{pmatrix} \\ \\ \huge \purple{Y = \begin{pmatrix} 0 & - 1 & - 3 \\ 1 & - 1 & - 1 \\ - 2 & 1 & - 2 \end{pmatrix}}\)
Find y
0
(t), the zero-input response of the response for an LTIC system described by (c) the complex-root system (D
2
+4D+40)y(t)=(D+2)x(t) with initial conditions y
0
(0)=2 and
y
˙
0
(0)=16.78.
Answers
The transform ,D2Y(s) + 4DY(s) + 40Y(s) = (D+2)X(s) Therefore, the zero-input response of the system y0(t) is given asy0(t) = (e -2t) - 2(cos6t + sin6t) + 6/5
Given that, LTIC system described by the complex-root system is given below.(D2+4D+40)y(t)=(D+2)x(t)
The zero-input response of the response for an LTIC system is given by the initial conditions. The initial condition for the given system is given below.y0(0)=2 and y˙0(0)=16.78.
Using the Laplace transform method, find the transfer function of the given system .
1: Finding the Laplace Transform for the given system(D2+4D+40)y(t)=(D+2)x(t). First, we need to take the Laplace transform of both sides of the given equation. We know that the Laplace transform of y(t) and x(t) are Y(s) and X(s) respectively. Therefore, we get,D2Y(s) + 4DY(s) + 40Y(s) = (D+2)X(s)
2: Solving for the Transfer Function. We know that transfer function is H(s)=Y(s)/X(s). Therefore, we getH(s)= (D+2)/(D2+4D+40)Taking the Laplace inverse of H(s) gives the zero-input response of the given system y0(t).
3: Finding the Zero-Input Response of the given system. We need to find the partial fraction of the transfer function. For that, solve the following equation.D2+4D+40 = 0. Using the quadratic formula, we get,D = -2 ± 6iTherefore, we get the partial fraction of the transfer function as, H(s)=1/(D+2) - 2/D + 3/5 + (3/5s)
Therefore, the zero-input response of the system y0(t) is given asy0(t) = (e -2t) - 2(cos6t + sin6t) + 6/5
Learn more about Laplace Transform here:
https://brainly.com/question/14487937
#SPJ11
The graph of f(x) = 2x is shown on the grid. (First attachment)
The graph of g(x) = (One-half)x is the graph of f(x) = 2x reflected over the y-axis. Which graph represents g(x)? (The rest of the attachments are the options)





Answers
The graph that represents the function g(x) = (1/2)^x is given as follows:
The last graph.
How to obtain the rule for function g(x)?The parent function f(x) has the definition presented as follows:
f(x) = 2^x.
The transformation that the function f(x) undergoes is defined as follows:
Reflection over the y-axis.
The rule that defines a function g(x) after a reflection of f(x) over the y-axis is given as follows:
g(x) = f(-x).
Hence the function g(x) is defined as follows:
g(x) = f(-x) = 2^(-x) = (1/2)^x.
As the negative exponent means that the base is inverted.
Then the graph of the exponential function has these following features:
Decreasing, as the base has an absolute value less than 1.Crosses the y-axis at y = 1, as when x = 0, y = (1/2)^0 = 1.Hence the last graph is the correct option.
More can be learned about reflections at https://brainly.com/question/28980122
#SPJ1
when the base-$b$ number $11011 b$ is multiplied by $b-1$, then $1001 b$ is added, what is the result (written in base $b$)?
Answers
we express the result in base $b$: $b^5 - 2b^4 + 3b^3 - 2b^2 + 2b^1 + b^0$ (written in base $b$)
To find the result when the base-$b$ number $11011_b$ is multiplied by $b-1$ and then $1001_b$ is added, we can follow these steps:
Step 1: Multiply $11011_b$ by $b-1$.
Step 2: Add $1001_b$ to the result from step 1.
Step 3: Express the final result in base $b$.
To perform the multiplication, we can expand $11011_b$ as $1 \cdot b^4 + 1 \cdot b^3 + 0 \cdot b^2 + 1 \cdot b^1 + 1 \cdot b^0$.
Now, we can distribute $b-1$ to each term:
$(1 \cdot b^4 + 1 \cdot b^3 + 0 \cdot b^2 + 1 \cdot b^1 + 1 \cdot b^0) \cdot (b-1)$
Expanding this expression, we get:
$(b^4 - b^3 + b^2 - b^1 + b^0) \cdot (b-1)$
Simplifying further, we get:
$b^5 - b^4 + b^3 - b^2 + b^1 - b^4 + b^3 - b^2 + b^1 - b^0$
Combining like terms, we have:
$b^5 - 2b^4 + 2b^3 - 2b^2 + 2b^1 - b^0$
Now, we can add $1001_b$ to this result:
$(b^5 - 2b^4 + 2b^3 - 2b^2 + 2b^1 - b^0) + (1 \cdot b^3 + 0 \cdot b^2 + 0 \cdot b^1 + 1 \cdot b^0)$
Simplifying further, we get:
$b^5 - 2b^4 + 3b^3 - 2b^2 + 2b^1 + b^0$
Finally, we express the result in base $b$:
$b^5 - 2b^4 + 3b^3 - 2b^2 + 2b^1 + b^0$ (written in base $b$)
Know more about base-$b$ here:
https://brainly.com/question/31939284
#SPJ11
I really need help...Will mark brainiest

Answers
Answer:
89999
Step-by-step explanation:
Rental of space = $68 per guest; Downpayment = 25% of total cost; Payment due one month before the reception includes a 7.4% interest payment on the balance.
Answers
This question is incomplete, the complete question is;
PROBLEM SOLVING WITH PERCENTS: You are planning a wedding reception for 75 guests that will take place in exactly 10 months. There are two different sites that you are contemplating using, with the stipulations on payments as described below. Determine the TOTAL cost of renting each location.
Rental of space = $68 per guest; Down payment = 25% of total cost; Payment due one month before the reception includes a 7.4% interest payment on the balance.
Answer: Total Cost of Renting = $5312.29
Step-by-step explanation:
Given that;
Rental space = $68 per guest, down payment = 25%, 7.4% interest payment on the balance.
Total Cost of Renting = Down Payment + Remaining payment
Total Cost of Renting = $68 × Guests × 25% + ($68 × Guest - Down payment) × (1 + Interest *9/12)
Total Cost of Renting = $68 × 75 × 25% + ($68 × 75 - Down payment) × (1 + 7.40% × 9/12)
Total Cost of Renting = $1275 + ($5100 - 1273) × (1.0555)
Total Cost of Renting = $1275 + 4037.29
Total Cost of Renting = $5312.29
FILL IN THE BLANK. if it is impossible for events a and b to occur simultaneously, the events are said to be mutually exclusive. for such events, p(a or b) _________.
Answers
If it is impossible for events A and B to occur simultaneously, the events are said to be mutually exclusive. For such events, P(A or B) is equal to the sum of the individual probabilities of events A and B.
In other words, if A and B are mutually exclusive events, the probability of A or B occurring is equal to the sum of the probabilities of A and B individually.
Mathematically, P(A or B) = P(A) + P(B).
This holds true because when two events are mutually exclusive, the occurrence of one event excludes the possibility of the other event happening at the same time. Therefore, there is no overlap in the outcomes, and we can simply add their probabilities to calculate the probability of either event occurring.
for such more question on probabilities
https://brainly.com/question/13604758
#SPJ11
plz help I will give thanks and if u give me the right answer ill give u brainly

Answers
Answer:8
Step-by-step explanation:
You are wanting a negative 1
So you start by getting to zero would take 7 “jumps”
Then u need to get into the negative by one
So when you go back one you get 8 jumps total
For 50 points can you help me with this I really need help.

Answers
The coordinates of the points in the table indicates that the coordinates of the image following the reflections, can be presented on the coordinate plane as shown in the attached graph created with MS Excel.
What is a reflection transformation?A reflection transformation is one in which the mirror image of the preimage is created across a line of reflection.
The coordinate points of the image after the specified reflections can be presented as follows;
Original \({}\)Reflection across the x-axis Reflection across the y-axis y = -x
(0, 15) \({}\) (0, -15) (0, 15) (-15, 0)
(1, 15) \({}\) (1, -15) (-1, 15) (-15, -1)
(1, 13) \({}\) (1, -13) (-1, 13) (-13, -1)
(3, 15) \({}\) (3, -15) (-3, 15) (-15, -3)
(3, 12) \({}\) (3, -12) (-3, 12) (-12, -3)
(1, 10) \({}\) (1, -10) (-1, 10) (-10, -1)
(1, 8) \({}\) (1, -8) (-1, 8) (-8, -1)
(3, 10) \({}\)(3, -10) (-3, 10) (-10, -3)
(3, 7) \({}\) (3, -7) (-3, 7) (-7, -3)
(1, 5) \({}\) (1, -5) (-1, 5) (-5, -1)
(1, 2) \({}\) (1, -2) (-1, 2) (-2, -1)
(4, 4) \({}\) (4, -4) (-4, 4) (-4, -4)
(5, 7) \({}\) (-5, 7) (5, -7) (-7, -5)
(7, 8) \({}\) (7, -8) (-7, 8) (-8, -7)
(6, 5) \({}\) (6, -5) (-6, 5) (-5, -6)
(8, 6) \({}\) (8, -6) (-8, 6) (-6, -8)
(9, 9) \({}\) (9, -9) (-9, 9) (-9, -9)
(11, 10) \({}\) (11, -10) (-11, 10) (-10, -11)
(10, 7) \({}\) (10, -7) (-10, 7) (-7, -10)
(12, 8) \({}\) (12, -8) (-12, 8) (-8, -12)
(13, 6) \({}\) (13, -6) (-13, 6) (-6, -13)
(11, 5) \({}\) (11, -5) (-11, 5) (-5, -11)
(14, 4) \({}\) (14, -4) \({}\) (-14, 4) (-4, -14)
(12, 3) \({}\) (12, -3) (-12, 3) (-3, -12)
(9, 4) \({}\) (9, -4) (-9, 4) (-4, -9)
(7, 3) \({}\) (7, -3) (-7, 3) (-3, -7)
(10, 2) \({}\) (10, -2) (-10, 2) (-2, -10)
(8, 1) \({}\) (8, -1) (-8, 1) (-1, -8)
(5, 2) \({}\) (5, -2) (-5, 2) (-2, -5)
(2, 0) \({}\) (2, 0) (-2, 0) (0, -2)
The above coordinate points can be used to plot the graphs showing the image of the points following the specified reflections across the x-, y-, and y = -x, axis.
Please find attached the required graph of the coordinate points following the reflection transformations, created with MS Excel.
Learn more on reflection transformation here: https://brainly.com/question/29080489
#SPJ1




Evaluate the following
expression using x = 5:
3(3x + 5)

Answers
\( \huge\color{skyblue}\boxed{\colorbox{black}{Answer ☘}}\)
Let's substitute x with 5 to find the value of given expression ~
\( \sf3[(3 \times 5) + 5]\)\( \sf3(15 + 5)\)\( \sf3(20)\)\( \sf60\)The value of the expression is 60.
What is the value of the expression?
According to the BODMAS rule, when there is a mathematical expression with a bracket, the terms in the bracket should be solved first. So the value of the expression in the bracket would be solved first.
(3(5) + 5)
(15 + 5)
= 20
The second step is to multiply 20 by 3.
20 x 3 = 60
To learn more about multiplication, please check: https://brainly.com/question/3385014
7. Find the corresponding angle.
(look at the picture)

Answers
Answer:
angle SXV
Step-by-step explanation:
Use the normal distribution curve to illustrate your answer
______________________________________________________________________
The following simple random sample was selected from a normal distribution: 4, 6, 3, 5, 9, and 3.
Construct a 90% confidence interval for the population mean μ.
Construct a 95% confidence interval for the population mean μ.
Construct a 99% confidence interval for the population mean μ.
Assume that the sample mean x and sample standard deviation s remain exactly the same as those you just calculated but that they are based on a sample of n = 25 observations rather than n = 6 observations. Repeat parts a-c. What is the effect of increasing the sample size on the width of the confidence intervals?
Answers
A) the 90% Confidence Interval is (2.424, 7.576). B) the 95% Confidence Interval is (2.24, 7.76).
C) the 99% Confidence Interval is (1.16, 8.84). D) When sample size is increased, the width of the confidence interval decreases, if all the other factors remain constant.
The given problem is based on normal distribution of data and confidence intervals. A confidence interval provides a range of values for an unknown population parameter; the interval has an associated level of confidence that the true parameter value falls in the interval. The confidence level gives the probability that the interval produced will contain the true parameter of interest. Below are the answers for the given questions.
a. 90% Confidence Interval:
Here, the given data is: 4, 6, 3, 5, 9, and 3.
To calculate the 90% Confidence Interval, we need to first calculate the sample mean and sample standard deviation of the given data.
Sample mean,
x¯ = (4 + 6 + 3 + 5 + 9 + 3) / 6 = 30 / 6 = 5
Sample standard deviation,
s = √[∑(xi - x¯)² / (n - 1)]
= √[(4 - 5)² + (6 - 5)² + (3 - 5)² + (5 - 5)² + (9 - 5)² + (3 - 5)² / (6 - 1)]
= √[14.0]
= 3.74166
Now, the Confidence Interval can be calculated as,
CI = x¯ ± Z_(α/2) (s / √n)
Where,
α = 1 - confidence level = 1 - 0.90 = 0.10
Z_(α/2) = Z_0.05 = 1.645 (From Z table)
CI = 5 ± 1.645 (3.74166 / √6)
CI = 5 ± 2.576
CI = (2.424, 7.576)
Therefore, the 90% Confidence Interval is (2.424, 7.576).
b. 95% Confidence Interval:
For a 95% Confidence Interval, α = 1 - 0.95 = 0.05 and Z_(α/2) = Z_0.025 = 1.96
CI = x¯ ± Z_(α/2) (s / √n)
CI = 5 ± 1.96 (3.74166 / √6)
CI = 5 ± 2.76
CI = (2.24, 7.76)
Therefore, the 95% Confidence Interval is (2.24, 7.76).
c. 99% Confidence Interval:
For a 99% Confidence Interval, α = 1 - 0.99 = 0.01 and Z_(α/2) = Z_0.005 = 2.58
CI = x¯ ± Z_(α/2) (s / √n)
CI = 5 ± 2.58 (3.74166 / √6)
CI = 5 ± 3.84
CI = (1.16, 8.84)
Therefore, the 99% Confidence Interval is (1.16, 8.84).
d. The effect of increasing the sample size on the width of the confidence intervals:
When sample size is increased, the width of the confidence interval decreases, if all the other factors remain constant. Here, sample mean and sample standard deviation are kept constant. Therefore, with larger sample sizes, the confidence intervals will become narrower.
Know more about Confidence Interval here,
https://brainly.com/question/32546207
#SPJ11