Suppose the average life for new tires is thought to be bell-shaped and symmetrical with a mean of 45,000 miles and a standard deviation of 4,000 miles Based on this information, what interval of miles would approximately 95% of tires be expected to last within?A 41000 10 49.000B. 42,000 to 47.000C 45,000 to 49.000D 37 000 to 53000
Answers
The interval of miles in which approximately 95% of tires are expected to last within is from 37,000 to 53,000 miles.
To answer your question, we'll use the given information about the bell-shaped and symmetrical distribution with a mean and standard deviation.
Mean (μ) = 45,000 miles
Standard Deviation (σ) = 4,000 miles
For a bell-shaped and symmetrical distribution, approximately 95% of the data falls within 2 standard deviations of the mean. We can use this to find the interval:
According to the empirical rule, approximately 95% of the data falls within two standard deviations of the mean. In this case, two standard deviations below the mean is 45,000 - (2*4,000) = 37,000 and two standard deviations above the mean is 45,000 + (2*4,000) = 53,000.
Lower Bound: μ - 2σ = 45,000 - 2(4,000) = 45,000 - 8,000 = 37,000 miles
Upper Bound: μ + 2σ = 45,000 + 2(4,000) = 45,000 + 8,000 = 53,000 miles
So, approximately 95% of tires would be expected to last within the interval of 37,000 to 53,000 miles. The correct answer is D. 37,000 to 53,000.
Learn more about Miles:
brainly.com/question/23245414
#SPJ11
Related Questions
Students at a high school are asked to evaluate their experience in the class at the end of each school year. The courses are evaluated on a 1-4 scale – with 4 being the best experience possible. In the History Department, the courses typically are evaluated at 10% 1’s, 15% 2’s, 34% 3’s, and 41% 4’s. Mr. Goodman sets a goal to outscore these numbers. At the end of the year he takes a random sample of his evaluations and finds 11 1’s, 14 2’s, 47 3’s, and 53 4’s. At the 0.05 level of significance, can Mr. Goodman claim that his evaluations are significantly different than the History Department’s?
Hypotheses:
H0: There is (no difference /a difference) in Mr. Goodman’s evaluations and the History Department’s.
H1: There is (no difference /a difference) in Mr. Goodman’s evaluations and the History Department’s.
Enter the test statistic - round to 4 decimal places.
Enter the p-value - round to 4 decimal places.
Can it be concluded that there is a statistically significant difference in Mr. Goodman’s evaluations and the History Department’s?
(Yes/ No)
Answers
It (B) cannot be determined that there is a statistically significant difference between Mr. Goodman's ratings and those of the History Department in the context of Mr. Goodmain and with all the material provided.
What is a random sample?In statistics, a simple random sample (or SRS) is a subset of people (a sample) picked at random from a larger group of people (a population), all with the same probability.
It is a method of choosing a sample at random. Each subset of k people in SRS has the same chance of getting selected for the sample as any other subset of k people.
An objective sampling strategy is a straightforward random sample. Simple random sampling is a fundamental kind of sampling that can be used in combination with other, more sophisticated sampling techniques.
So, in the given situation of Mr. Goodmain and with all the information given we can conclude that it cannot be concluded that there is a statistically significant difference in Mr. Goodman’s evaluations and the History Department’s.
Therefore, it (B) cannot be determined that there is a statistically significant difference between Mr. Goodman's ratings and those of the History Department in the context of Mr. Goodmain and with all the material provided.
Know more about a random sample here:
https://brainly.com/question/24466382
#SPJ4
Complete question:
Students at a high school are asked to evaluate their experience in the class at the end of each school year. The courses are evaluated on a 1-4 scale – with 4 being the best experience possible. In the History Department, the courses typically are evaluated at 10% 1’s, 15% 2’s, 34% 3’s, and 41% 4’s. Mr. Goodman sets a goal to outscore these numbers. At the end of the year, he takes a random sample of his evaluations and finds 11 1’s, 14 2’s, 47 3’s, and 53 4’s. At the 0.05 level of significance, can Mr. Goodman claim that his evaluations are significantly different than the History Departments?
Hypotheses:
H0: There is (no difference /difference) in Mr. Goodman’s evaluations and the History Department’s.
H1: There is (no difference /difference) in Mr. Goodman’s evaluations and the History Department’s.
Enter the test statistic - round to 4 decimal places.
Enter the p-value - round to 4 decimal places.
Can it be concluded that there is a statistically significant difference between Mr. Goodman’s evaluations and the History Department’s?
a. Yes
b. No
A production process produces an item. On average, 15% of all items produced are defective. Each item is inspected before being shipped, and the inspector misclassifies an item 10% of the time. What proportion of the items will be "classified as good"? What is the probability that an item is defective given that it was classified as good?
Answers
The approximately 1.5% of the items will be classified as good.
The probability that an item is defective given that it was classified as good is around 1.96%.
When we consider the production process, we know that 15% of all items produced are defective. However, the inspector misclassifies an item 10% of the time. This means that out of the 85% of non-defective items, approximately 10% will be falsely classified as defective.
Hence, the proportion of items classified as good can be calculated as 100% - 10% = 90% of non-defective items. Considering that 85% of all items produced are non-defective, we can estimate that 85% * 90% = 76.5% of all items will be classified as good.
To determine the probability that an item is defective given that it was classified as good, we need to consider the misclassification rate. Since the inspector misclassifies an item 10% of the time, it means that out of the 15% defective items, around 10% will be incorrectly classified as good. Thus, the proportion of items classified as good but are actually defective can be calculated as 15% * 10% = 1.5%.
Therefore, the probability that an item is defective given that it was classified as good is approximately 1.5% out of the total items classified as good, which is 76.5%. Consequently, the probability that an item is defective given that it was classified as good is approximately 1.5% / 76.5% = 1.96%.
Learn more about Probability
brainly.com/question/11034287
#SPJ11
Tom earns $30 a week mowing lawns. he spends 1/6 of his earnings on lunch and 1/3 of his earnings on music . he saves the rest . How many dollars does Tom save?
Answers
he would have around 7 $ left hope this help
asap please !
In a state assembly, 35% of the legislators are Democrats, and the other 65% are Republicans. 70% of the Democrats favor raising sales tax, while only 40% of the Republicans favor the increase. If a legislator is selected at random from this group, what is the probability that they favor raising sales tax? Give your answer as a percentage rounded to the nearest tenth.
Answers
Answer:
Probability of selecting a legislator who favors rising sales tax is 0.63
Step-by-step explanation:
Given
Percentage of legislators that are democrats = 0.35
Percentage of legislators that are Republicans = 0.70
All the democrats favor raise in sales tax , so their probability is 1
and only 40% of the Republicans favor raise in sales tax.
Probability of selecting a legislator who favors rising sales tax is
(0.35*1)+(0.70*0.40)
= 0.63
What is AB?
Please hurry answer
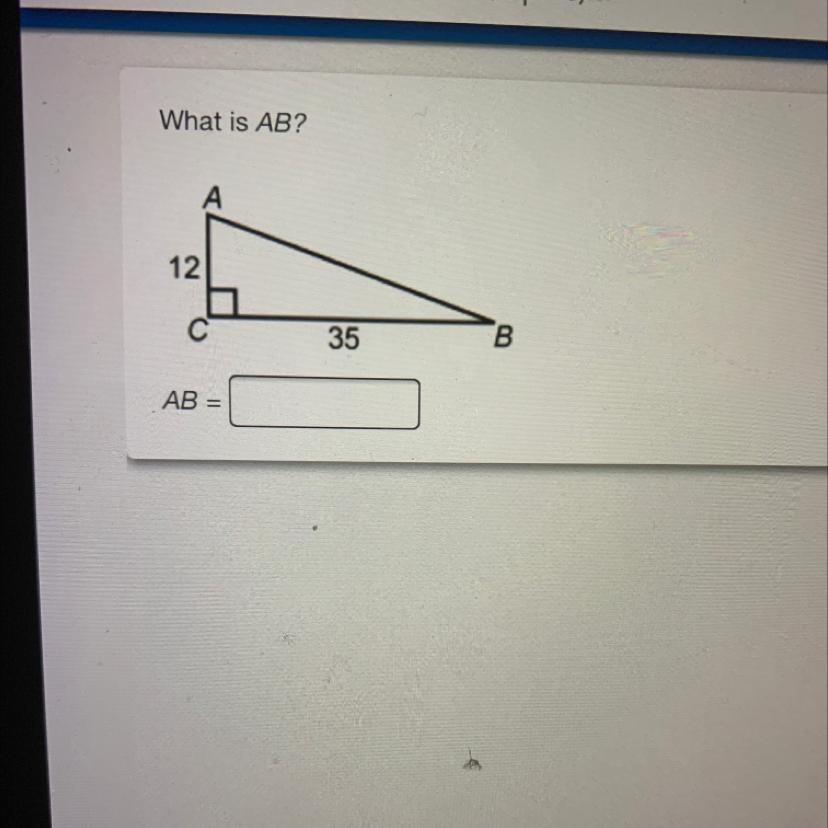
Answers
Answer:
The Answer is 47
Step-by-step explanation:
Because you do A squared plus B squared equals C squared and Squared is just multiplying both by two.
A report card shows that a student earns 21 21 points on a test with a total of 25 25 points. What percentage of the total points has the student earned on the test?.
Answers
When a report card shows that a student has earned 21 points on a test with a total of 25 points, it can be concluded to state that the student has secured 84 percentage of the total points of the test.
The computation of the percentage of points secured by the student out of the total available points in a test can be done using the generalized formula and the use of provided information into the same as below,
Percentage = Scored Secured / Total Points x 100
Percentage = 21 / 25 × 100
Percentage = 0.84 × 100
Percentage = 84 percentage.
Therefore, the student has earned 84 percentage of total points on a test.
Learn more about percentage here:
https://brainly.com/question/29306119
#SPJ4
Help me with this pleae

Answers
Answer:
0
x
Step-by-step explanation:
You’re basically doing what you did for the first one.
Just swap places.
What is the reason for each step in the solution of the equation
12-5x+6x=4

Answers
Answer: x=-8
Step-by-step explanation: 12-5x+6x=4 1. Combine like terms: -5x+6x+12=4 2. Simplify: x+12-12=4-12 3. Subtract 4 from -12 so that you can find out what x is: x=-8
what are all operations with fractions that require a common denominator
Answers
Answer:
Adding Fractions: If the denominators are not the same, you must find the common denominator by finding the least common multiple (LCM). Subtracting Fractions: If the denominators are not the same, you must find the common denominator by finding the least common multiple (LCM).
if 104=10,000, which is equal to 4? select the correct answer below: log100 log1,000 log10,000 log4 log40,000
Answers
The correct answer is log4. The given statement is 10^4 = 10,000. To find the value equal to 4, we need to look for the logarithm with a base of 10 that results in 4.
In this case, the correct answer is log10,000 because log10(10,000) = 4. This is because log is the inverse operation of exponentiation. In other words, log4 is asking the question "what power do I need to raise 10 to in order to get 4?"
We know that 104 is equal to 10,000, so we can rewrite the question as "what power do I need to raise 10 to in order to get 10,000?" The answer is 4, since 10 to the power of 4 is 10,000. Therefore, log10,000 is equal to 4.
Learn more about inverse operation here:
brainly.com/question/1210406
#SPJ11
if 8^{y}=18^{y+2} what is the value of y?

Answers
Answer:
-8
Step-by-step explanation:
both 8^-8 and 16^-8+2 equal 5.9605
\([Hello,BrainlyUser]\)
Answer:
y = -8
Step-by-step explanation:
Create equivalent expressions in the equation that all have equal bases.
\(2^3^y=2^4^(^y^+^2^)\)
Since the bases are the same, then two expressions are only equal if the exponents are also equal.
\(3y=4(y+2)\)
Simplify
\(4(y+2).\)
Apply the distributive property.
\(3y=4y+4*2\)
Multiply 4 by 2
\(3y=4y+8\)
Subtract 4y from both sides of the equation.
\(3y-4y=8\)
Subtract 4y from 3y.
\(-y=8\)
Multiply each term in −y=8 by −1
\(y=-8\)
Hence, Answer is y = -8
[CloudBreeze]
The following table shows a proportional relationship between x and y.
x y
2 9
5 22.5
8 36
Write an equation to describe the relationship between x and y.
Answers
Answer:
Assume x is directly proportional to y :
\(y \: \alpha \: x \\ y = kx\)
when y is 9, x is 2:
substitute to find value of k :
\(9 = (k \times 2) \\ k = \frac{9}{2} \)
Therefore, equation is:
\({ \boxed{ \boxed{2y = 9 x}}}\)
For the following set of data, find the percentage of data within 2 population standard deviations of the mean, to the nearest percent
chart is in the photo

Answers
Percentage of data within 2 population standard deviations of the mean is 68%.
To calculate the percentage of data within two population standard deviations of the mean, we need to first find the mean and standard deviation of the data set.
The mean can be found by summing all the values and dividing by the total number of values:
Mean = (20*2 + 22*8 + 28*9 + 34*13 + 38*16 + 39*11 + 41*7 + 48*0)/(2+8+9+13+16+11+7) = 32.68
To calculate standard deviation, we need to calculate the variance first. Variance is the average of the squared differences from the mean.
Variance = [(20-32.68)^2*2 + (22-32.68)^2*8 + (28-32.68)^2*9 + (34-32.68)^2*13 + (38-32.68)^2*16 + (39-32.68)^2*11 + (41-32.68)^2*7]/(2+8+9+13+16+11+7-1) = 139.98
Standard Deviation = sqrt(139.98) = 11.83
Now we can calculate the range within two population standard deviations of the mean. Two population standard deviations of the mean can be found by multiplying the standard deviation by 2.
Range = 2*11.83 = 23.66
The minimum value within two population standard deviations of the mean can be found by subtracting the range from the mean and the maximum value can be found by adding the range to the mean:
Minimum Value = 32.68 - 23.66 = 9.02 Maximum Value = 32.68 + 23.66 = 56.34
Now we can count the number of data points within this range, which are 45 out of 66 data points. To find the percentage, we divide 45 by 66 and multiply by 100:
Percentage of data within 2 population standard deviations of the mean = (45/66)*100 = 68% (rounded to the nearest percent).
Therefore, approximately 68% of the data falls within two population standard deviations of the mean.
for more such questions on population
https://brainly.com/question/30396931
#SPJ8
Q4. Renna went on a journey that took 712 hours. The journey started at 22 48 on Monday. At what time and day did the journey finish?
Answers
Answer:
Step-by-step explanation:
Divide 712 hours by 24 hours/day, obtaining 29 2/3 days, which in turn breaks down into 28 days plus 1 2/3 days, or 4 weeks plus 1 2/3 days. '4 weeks' takes us to a Monday, 22:48, 4 weeks after the start of the journey.
To this we add 1 2/3 days, reaching 16 hours into the Tuesday immediately following that Monday. That would be approximately 16:00 on that Tuesday, but we must work backwards 1:12 hours: subtracting 1:12 from 16:00 on Tuesday yields 14:48
The journey finishes at 14:48 4 weeks and 1 day after it began.
Giant Corporation is considering a major equipment purchase is being considered. The initial cost is determined to be $1,000,000. It is estimated that this new equipment will save $100,000 the first year and increase gradually by $50,000 every year for the next 6 years. MARR=10%. Briefly discuss. a. Calculate the payback period for this equipment purchase. b. Calculate the discounted payback period c. Calculate the Benefits Cost ratio d. Calculate the NFW of this investment Problem 2: Below are four mutually exclusive alternatives given in the table below. Assume a life of 7 years and a MARR of 9%. Alt. A Alt. B Alt. C Initial Cost $5,600 EUAB $1,400 Salvage Value $400 $3,400 $1,000 $0 $1,200 $400 $0 Alt. D - Do Nothing $0 $0 $0 a. The AB /AC ratio for the first increment, (C-D) is how much? b. The AB /AC ratio for the second increment, (B-C) is how much? c. The AB /AC ratio for the third increment, (A-B) is how much? d. The best alternative using B/C ratio analysis is which one and why?
Answers
a. The payback period for the equipment purchase is 8 years.
b. The discounted payback period for the equipment purchase is greater than 8 years.
c. The Benefits Cost ratio for the equipment purchase is 1.39.
d. The Net Future Worth (NFW) of this investment is positive.
a. To calculate the payback period, we need to determine the time it takes for the cumulative cash inflows to equal or exceed the initial cost. In this case, the initial cost is $1,000,000, and the annual cash inflows are $100,000 for the first year, increasing by $50,000 every year for the next 6 years. We calculate the cumulative cash inflows as follows:
Year 1: $100,000
Year 2: $100,000 + $50,000 = $150,000
Year 3: $100,000 + $50,000 + $50,000 = $200,000
Year 4: $100,000 + $50,000 + $50,000 + $50,000 = $250,000
Year 5: $100,000 + $50,000 + $50,000 + $50,000 + $50,000 = $300,000
Year 6: $100,000 + $50,000 + $50,000 + $50,000 + $50,000 + $50,000 = $350,000
Year 7: $100,000 + $50,000 + $50,000 + $50,000 + $50,000 + $50,000 + $50,000 = $400,000
The payback period is the time it takes for the cumulative cash inflows to reach or exceed the initial cost. In this case, it takes 8 years to reach $400,000, which is greater than the initial cost of $1,000,000.
b. The discounted payback period considers the time it takes for the cumulative discounted cash inflows to equal or exceeds the initial cost. We need to discount the cash inflows using the MARR (10%). The discounted cash inflows are as follows:
Year 1: $100,000 / (1 + 0.10)^1 = $90,909.09
Year 2: $50,000 / (1 + 0.10)^2 = $41,322.31
Year 3: $50,000 / (1 + 0.10)^3 = $37,566.64
Year 4: $50,000 / (1 + 0.10)^4 = $34,151.49
Year 5: $50,000 / (1 + 0.10)^5 = $31,046.81
Year 6: $50,000 / (1 + 0.10)^6 = $28,223.46
Year 7: $50,000 / (1 + 0.10)^7 = $25,645.87
The cumulative discounted cash inflows are calculated as follows:
Year 1: $90,909.09
Year 2: $90,909.09 + $41,322.31 = $132,231.40
Year 3: $132,231.40 + $37,566.64 = $169,798.04
Year 4: $169,798.04 + $34,151.49 = $203,949.53
Year 5: $203,949.53 + $31,046.81 = $235,996.34
Year 6: $235,996.34 + $28,223.46 = $264,219.80
Year 7: $264,219.80 + $25,645.87 = $289,865.67
The discounted payback period is the time it takes for the cumulative discounted cash inflows to reach or exceed the initial cost. In this case, it takes more than 8 years to reach $289,865.67, which is greater than the initial cost of $1,000,000.
c. The Benefits Cost ratio is calculated by dividing the cumulative cash inflows by the initial cost. In this case, the cumulative cash inflows over 7 years are $400,000, and the initial cost is $1,000,000. Therefore, the Benefits Cost ratio is 0.4 (400,000/1,000,000).
d. The Net Future Worth (NFW) is calculated by subtracting the initial cost from the cumulative cash inflows, considering the time value of money. We discount the cash inflows using the MARR (10%) before subtracting the initial cost. The discounted cash inflows are as follows:
Year 1: $100,000 / (1 + 0.10)^1 = $90,909.09
Year 2: $50,000 / (1 + 0.10)^2 = $41,322.31
Year 3: $50,000 / (1 + 0.10)^3 = $37,566.64
Year 4: $50,000 / (1 + 0.10)^4 = $34,151.49
Year 5: $50,000 / (1 + 0.10)^5 = $31,046.81
Year 6: $50,000 / (1 + 0.10)^6 = $28,223.46
Year 7: $50,000 / (1 + 0.10)^7 = $25,645.87
The cumulative discounted cash inflows are calculated as follows:
Year 1: $90,909.09
Year 2: $90,909.09 + $41,322.31 = $132,231.40
Year 3: $132,231.40 + $37,566.64 = $169,798.04
Year 4: $169,798.04 + $34,151.49 = $203,949.53
Year 5: $203,949.53 + $31,046.81 = $235,996.34
Year 6: $235,996.34 + $28,223.46 = $264,219.80
Year 7: $264,219.80 + $25,645.87 = $289,865.67
The NFW is calculated as the cumulative discounted cash inflows minus the initial cost:
NFW = $289,865.67 - $1,000,000 = -$710,134.33
The NFW of this investment is negative, indicating that the investment does not yield positive net benefits considering the MARR (10%).
Problem 2:
a. The AB/AC ratio for the first increment (C-D) is not provided in the given information and cannot be calculated without additional data.
b. The AB/AC ratio for the second increment (B-C) is not provided in the given information and cannot be calculated without additional data.
c. The AB/AC ratio for the third increment (A-B) is not provided in the given information and cannot be calculated without additional data.
d. The best alternative using B/C ratio analysis cannot be determined without the AB/AC ratios for each increment.
For more questions like Cash click the link below:
https://brainly.com/question/10714011
#SPJ11
Consider the joint PDF of two random variables X, Y given by fX,Y(x,y)=c, where 0≤x≤a where a=5.18, and 0≤y≤4.83. Find fX(a2).
Answers
The value of \(\(f_X(a^2)\)\) is \(\(c \cdot 4.83\)\).
To find \(\(f_X(a^2)\),\) we need to integrate the joint PDF \(\(f_{X,Y}(x,y)\)\) over the range where \(X\) takes the value \(a^2\)
Given that \(\(f_{X,Y}(x,y) = c\)\) for \(\(0 \leq x \leq a = 5.18\)\) and \(\(0 \leq y \leq 4.83\)\), we can write the integral as follows:
\(\[f_X(a^2) = \int_{0}^{4.83} f_{X,Y}(a^2, y) \, dy\]\)
Since \(\(f_{X,Y}(x,y)\)\) is constant within the given range, we can pull it out of the integral:
\(\[f_X(a^2) = c \int_{0}^{4.83} \, dy\]\)
Evaluating the integral:
\(\[f_X(a^2) = c \cdot [y]_{0}^{4.83}\]\)
\(\[f_X(a^2) = c \cdot (4.83 - 0)\]\)
\(\[f_X(a^2) = c \cdot 4.83\]\)
Hence, the value of \(\(f_X(a^2)\)\) is \(\(c \cdot 4.83\)\).
Integral is defined as being, containing, or having to do with one or more mathematical integers. (2) pertaining to or having to do with mathematical integration or the outcomes thereof. generated in concert with another component. a chair with a built-in headrest.
To learn more about integral from the given link
https://brainly.com/question/30094386
#SPJ4
The linear function f(x) contains the points (-10, -29) and (-2, 83).
If g(x) = 19x - 25, which statement is true?
A.
The function f(x) has a positive slope, and the function g(x) has a negative slope.
B.
The functions f(x) and g(x) both have negative slopes.
C.
The function f(x) has a negative slope, and the function g(x) has a positive slope.
D.
The functions f(x) and g(x) both have positive slopes.
Answers
The functions f(x) and g(x) both have positive slopes. Thus, option D is correct.
What is the slope of a line which passes through points ( p,q) and (x,y)?Its slope would be:
\(m = \dfrac{y-q}{x-p}\)
Slope of parallel lines are same. Slopes of perpendicular lines are negative reciprocal of each other.
The linear function f(x) contains the points (-10, -29) and (-2, 83).
If g(x) = 19x - 25
Where the slope is m = 19
The slope of linear function f(x)
n = 83 -(-29) / -2 -(-10)
n = 112/ 8
n = 14
Therefore, we can see that the functions f(x) and g(x) both have positive slopes.
Thus, option D is correct.
Learn more about slope here:
https://brainly.com/question/2503591
#SPJ1
Factor the following:
36x^2 - 49
What is the vocabulary word describing the factors that result in this answer?
Answers
Answer:
(6x+7)(6x-7)
Step-by-step explanation:
This is an example of "Difference Of Squares".
Answer:
(6x - 7)(6x + 7).
The difference of 2 squares.
Step-by-step explanation:
Note that 36x^2 and 49 are perfect squares.
36x^2 - 49
= (6x - 7)(6x + 7).
need this please !!!!

Answers
Answer:
13.89 miles
Step-by-step explanation:
Since we are calculating for hypotenuse, reference Pythagorean Theorem:
a^2 + b^2 = c^2
12^2 + 7^2 = c^2
144 + 49 = 193
square root of 193 = 13.89 (If rounded to hundredths place)
Answer:
√(193) miles
Step-by-step explanation:
7²+12²=x²
49+144=x²
193=x²
x=√(193) miles
What is your estimated project completion time?
Please show work.
\begin{tabular}{|l|l|l|l|l|} \hline Activity & a & m & b & Immediate Predecessor \\ \hline A & 1 & 2 & 3 & \( \cdots \) \\ \hline B & 2 & 3 & 4 & \( \cdots \) \\ \hline C & 4 & 5 & 6 & A \\ \hline D &
Answers
To find the estimated project completion time for the given project activities, we need to first calculate the earliest start and earliest finish times and then the latest start and latest finish times.
Using the activity times given, we can calculate the earliest start and earliest finish times for each activity as follows: Activity A: Earliest start time = 0
Earliest finish time = 1
Activity B: Earliest start time = 2
Earliest finish time = 5
Activity C: Earliest start time = 5
Earliest finish time = 11
Activity D: Earliest start time = 11
Earliest finish time = 17
Activity E: Earliest start time = 5
Earliest finish time = 8 Activity F:
Earliest start time = 8
Earliest finish time = 17
Now we can calculate the latest start and latest finish times for each activity using the backward pass.
Latest finish time = 5
Latest start time = 2
Activity A: Latest finish time = 1
Latest start time = 0
Now we can calculate the slack time for each activity as follows:Activity A:
Slack time = 0
Activity B: Slack time = 0
Activity C: Slack time = 0
Activity D: Slack time = 0
Activity E: Slack time = 3
Activity F: Slack time = 0
The critical path for this project is A -> C -> D, since these activities have zero slack time. Therefore, the estimated project completion time is 17 units of time.
To know more about calculate visit:
https://brainly.com/question/30151794
#SPJ11
how to find the quotient and remainder of a polynomial
Answers
The polynomial 2x^3 - 4x^2 + 3x - 7 has the remainder is -1, and the quotient is 2x^2 + 3.
To find the quotient and remainder of a polynomial, follow these steps:
Arrange the polynomials in descending order of degrees.
Divide the term with the highest degree of the dividend polynomial by the term with the highest degree of the divisor polynomial. This will be the first term of the quotient.
Multiply the divisor polynomial by the first term of the quotient and subtract the result from the dividend polynomial.
Bring down the next term from the dividend polynomial.
Repeat steps 2 to 4 until all the terms of the dividend polynomial are exhausted or the degree of the remaining polynomial is lower than the degree of the divisor polynomial.
The resulting polynomial after the division process is complete is the remainder.
The terms obtained during the division process form the quotient polynomial.
For example, let's divide the polynomial 2x^3 - 4x^2 + 3x - 7 by the polynomial x - 2.
The term with the highest degree in the dividend polynomial is 2x^3, and the term with the highest degree in the divisor polynomial is x.
Dividing 2x^3 by x gives 2x^2, which is the first term of the quotient.
Multiply (x - 2) by 2x^2, giving 2x^3 - 4x^2.
Subtracting 2x^3 - 4x^2 from the dividend polynomial gives 3x - 7.
Bring down the next term, which is 3x.
Dividing 3x by x gives 3, which is the next term of the quotient.
Multiply (x - 2) by 3, giving 3x - 6.
Subtracting 3x - 6 from the remaining polynomial gives -7 + 6 = -1.
Since the degree of -1 is lower than the degree of x - 2, the division process is complete.
The remainder is -1, and the quotient is 2x^2 + 3.
Learn more about polynomial here:
https://brainly.com/question/11536910
#SPJ11
Solve this differential equation:
dydt=0.09y(1−y500)dydt=0.09y(1-y500)
y(0)=5y(0)=5
y(t) =
Answers
The conclusion is:
y(t) = (500e^(0.09t+ln(99))) / (1 + e^(0.09t+ln(99)))
Find out the solution for this differential equation?We have the differential equation:
dy/dt = 0.09y(1 - y/500)
To solve this, we can separate variables and integrate both sides:
dy / (y(1 - y/500)) = 0.09 dt
We can use partial fractions to break up the left-hand side:
dy / (y(1 - y/500)) = (1/500) (1/y + 1/(500 - y)) dy
Now we can integrate both sides:
∫ (dy / (y(1 - y/500))) = ∫ (1/500) (1/y + 1/(500 - y)) dy
ln |y| - ln |500 - y| = 0.09t + C
where C is the constant of integration.
Simplifying:
ln |y / (500 - y)| = 0.09t + C
Taking the exponential of both sides:
|y / (500 - y)| = e^(0.09t+C)
Since y(0) = 5, we can use this initial condition to find the value of C:
|5 / (500 - 5)| = e^C
C = ln(495/5)
C = ln(99)
So the equation becomes:
|y / (500 - y)| = e^(0.09t + ln(99))
Simplifying further:
y / (500 - y) = ± e^(0.09t + ln(99))
y = (500e^(0.09t+ln(99))) / (1 ± e^(0.09t+ln(99)))
Using the initial condition y(0) = 5, we can determine that the positive sign is appropriate:
y = (500e^(0.09t+ln(99))) / (1 + e^(0.09t+ln(99)))
Therefore, the solution to the differential equation is:
y(t) = (500e^(0.09t+ln(99))) / (1 + e^(0.09t+ln(99)))
Learn more about Equation
brainly.com/question/13763238
#SPJ11
Can someone tell me the answer for this please?

Answers
Every 10 nights, she knits 30cm of the scarf.
Take 30cm and divide it by 10 days and you will get 3cm per day
Ari exercises 1 5/8 hours per day. If he exercises five days a week, how many total hours does he exercise in a week?
HELPP\ PLEASE / QUICKLY !!!!!!!\
Answers
Answer:
8.125
Step-by-step explanation:
Just do 1 and 5/8 times 5
Answer:
8 1/8 hours a week
Step-by-step explanation:
I 5/8 times 5 gives me the product of 8.125. After converting that to a mixed number, you get 8 1/8.
You're welcome.
A six-sided die is rolled 2 times. What is the fractional probability of rolling different numbers?
Answers
Answer:
The probability of getting 6 the first time and an even number the second time is 1/12.
what is probability?
probability is the quantification of possibilities in numbers.
(1) probability of rolling a 6 for the first time:
total possible outcomes = (1,2,3,4,5,6) =6
sample space = 1
probability of getting 6 = sample space/total possible outcomes
probability of getting 6 = 1/6
2)probability of getting an even number
total possible outcomes will be (1,2,3,4,5,6)
sample space = (2,4,6) ie 3
probability of this = 3/6 = 0.5
total probability = 1/6*0.5 = 1/12
therefore,
The probability of getting 6 the first time and an even number the second time is 1/12.
to get more about probability refer to:
Step-by-step explanation:
is lmn a right triangle

Answers
Answer:true
Step-by-step explanation:
Answer:
true
Step-by-step explanation:
A map of the Hill Park hiking trails uses the scale
12 inch = 34 mile
.
Which unit rate is equivalent to this scale?
Answers
Answer:
wish i could help
Step-by-step explanation:
1
1
2
2
s
What is the measure in radians of central angle theta in the circle below?

Answers
Answer:
Θ = 5 radians
Step-by-step explanation:
arc length is calculated as
arc = circumference of circle × fraction of circle
here arc length = 15 , then
2πr × \(\frac{0}{2\pi }\) = 15 ( r is the radius )
2π × 3 × \(\frac{0}{2\pi }\) = 15 ( cancel 2π on numerator/ denominator )
3Θ = 15 ( divide both sides by 3 )
Θ = 5 radians
1) Explain the problem of unit root in standard regression and in time-series models and Explain how to use the Dickey-Fuller and augmented Dickey-Fuller tests to detect this. In clearly and detailed . Kindly type your answers . Course Econometrics
Answers
The problem of unit root in standard regression and time-series models arises when a variable exhibits a non-stationary behavior, meaning it has a trend or follows a random walk. Unit root tests, such as the Dickey-Fuller and augmented Dickey-Fuller tests, are used to detect the presence of a unit root in a time series. These tests examine whether the coefficient on the lagged value of the variable is significantly different from one, indicating the presence of a unit root.
In standard regression analysis, it is typically assumed that the variables are stationary, meaning they have a constant mean and variance over time. However, many economic and financial variables exhibit non-stationary behavior, where their values are not centered around a fixed mean but instead follow a trend or random walk. This presents a problem because standard regression techniques may produce unreliable results when applied to non-stationary variables.
Time-series models, such as autoregressive integrated moving average (ARIMA) models, are specifically designed to handle non-stationary data. They incorporate differencing techniques to transform the data into a stationary form, allowing for reliable estimation and inference. Differencing involves computing the difference between consecutive observations to remove the trend or random walk component.
The Dickey-Fuller test and augmented Dickey-Fuller test are commonly used to detect the presence of a unit root in a time series. These tests examine the coefficient on the lagged value of the variable in a regression framework. The null hypothesis of the tests is that the variable has a unit root, indicating non-stationarity, while the alternative hypothesis is that the variable is stationary.
The Dickey-Fuller test is a simple version of the test that includes only a single lagged difference of the variable in the regression. The augmented Dickey-Fuller test extends this by including multiple lagged differences to account for potential serial correlation in the data. Both tests provide critical values that can be compared to the test statistic to determine whether the null hypothesis of a unit root can be rejected.
To learn more about regression click here: brainly.com/question/32505018
#SPJ11
In order to isolate the variable term in the equation 6 -2x = -3 using the subtraction property of equality, which number
should be subtracted from both sides of the equation?
-3
-2
3
6
Answers
Answer:
6
Step-by-step explanation:
The reason you would do 6 is because you need to isolate the variable term.
This means you need the variable and its coefficient alone. so if you subtract 6 from each side of the equation you can achieve that goal. So the equation would then read -2x= -9 (because you combine the like terms of -6 and the -3 that was already there)
If you need to complete the rest of the equation you would divide both sides by -2 to further isolate x. This means x= 9/2 (since they are both negative they cancel each other out turning it positive) and the simplified answer would be 4 1/2
Hope this helps <3