System of equations- does this have one solution, many solutions or no solution
y=4x-12
y=-12+4x
Answers
Answer:
infinitely many solutions because both equations are the same
Step-by-step explanation:
Related Questions
Which place value should you use to compare the numbers?
645,853
646,34
Answers
The length of a side of an equilateral triangle is x-4.5 .
Create a model of an equilateral triangle, making sure to label the lengths of each side.
Add images
Answers
Answer:
Equilateral triangle means all sides have equal length.
Perimeter
As a sum: (x-4.5)+(x-4.5)+(x-4.5)
As a product: 3 * (x-4.5)
They are equivalent because 3 times a number is just the sum of three of the number.
Step-by-step explanation:
If a ball is dropped on the ground from a height of h m, then the ball reaches the ground with the
velocity V=4.43√h m/sec. Find the velocity with which a ball reaches the ground when it is dropped
from a height of 64 m.
Answers
The velocity with which a ball reaches the ground when it is dropped
from a height of 64 m is 35.44m/sec
How to determine the valueFrom the information given, we have that the equation representing the velocity of the ball is expressed as;
V = 4.43√h
Given that the parameters of the formula are;
V is the velocity of the ball from he ground.h is the height of the ball.Since the height of the ball from the ground is 64m, we have to substitute the value, we have;
V = 4.43√64
Find the square root of the value
V= 4.43(8)
Now, multiply both the values to determine the velocity, we get;
V = 35.44m/sec
Learn about velocity at: https://brainly.com/question/25749514
#SPJ1
certain kind of sheet metal has, on average, 7 defects per 20 square feet. assuming a poisson distribution, find the probability that a 34 square foot metal sheet has at least 9 defects. round your answer to four decimals.
Answers
The probability that a 34 square foot metal sheet has at least 9 defects is 0.4308, rounded to four decimals.
Given that the sheet metal has an average of 7 defects per 20 square feet, we can find the rate parameter (λ) of the Poisson distribution as follows:
λ = (7 defects / 20 sq ft) = 0.35 defects per square foot
Let X be the number of defects in a 34 square foot metal sheet. Since X follows a Poisson distribution with rate parameter λ, we can find the probability that X is at least 9 defects using the cumulative distribution function (CDF) of the Poisson distribution:
P(X ≥ 9) = 1 - P(X < 9) = 1 - F(8)
where F(k) is the CDF of the Poisson distribution with rate parameter λ evaluated at k.
Using the Poisson distribution formula for F(k), we have:
F(k) = P(X ≤ k) = ∑(i=0 to k) [(λ^i * e^(-λ)) / i!]
Using a calculator or software, we can find that:
F(8) = P(X ≤ 8) = 0.5692
Therefore, we have:
P(X ≥ 9) = 1 - F(8) = 1 - 0.5692 = 0.4308
To learn more about probability here:
https://brainly.com/question/30034780
#SPJ4
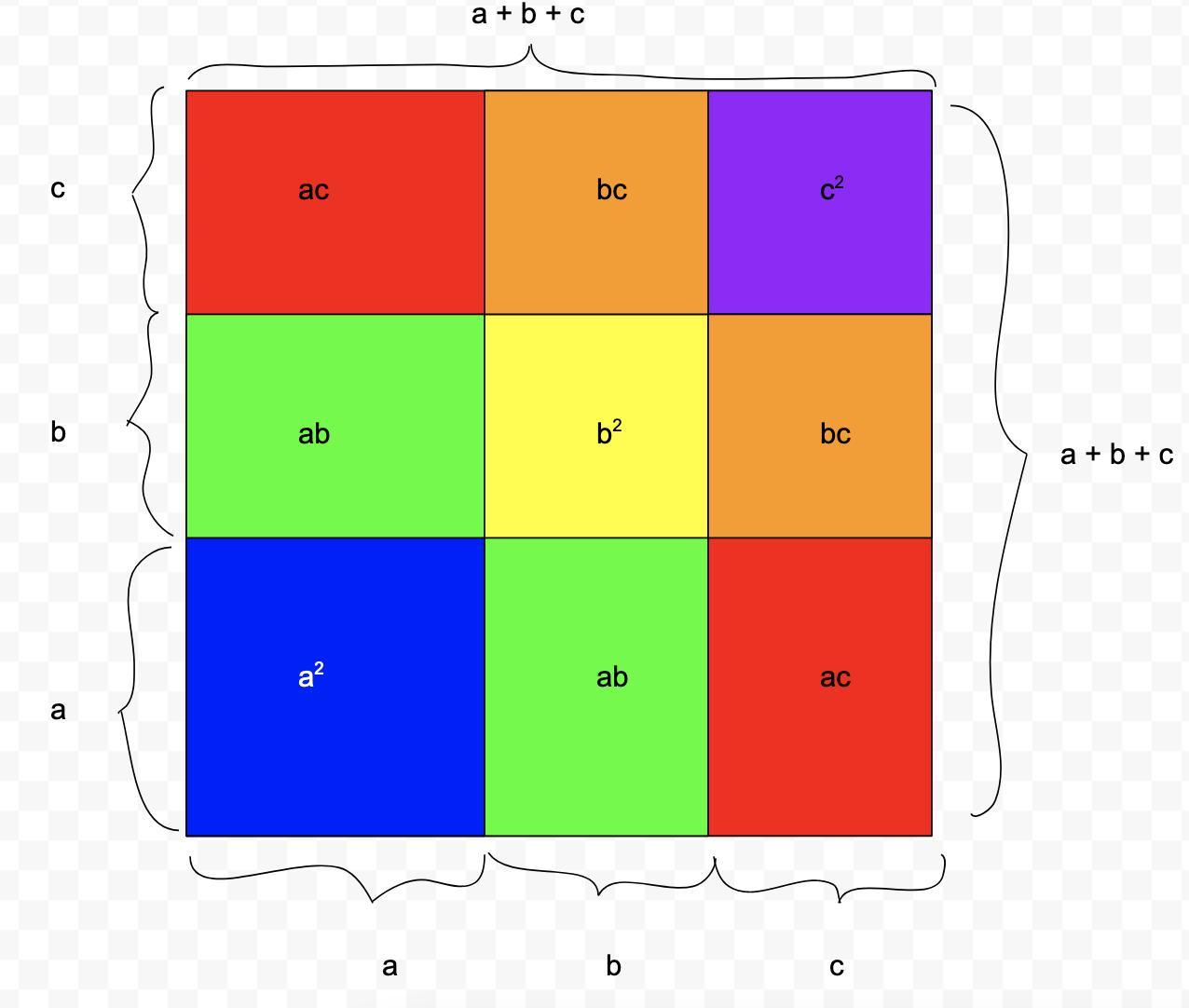
Verify the geometrical representation ofI) (a+b+c)^2
Answers
Presumably you're talking about a geometrical interpretation of the identity,
(a + b + c)² = a ² + b ² + c ² + 2 (ab + ac + bc)
See the attached sketch for a visual "proof" of it.
A random sample of 16 statistics examinations from a large population was taken. The average score in the sample was 78.6 with a standard deviation of 8. We are interested in determining whether the average grade of the population is significantly more than 75. The test statistic is: 3.6 045
Answers
A random sample of 16 statistics examinations from a large population was taken. The test statistic (t) for this hypothesis test is 1.8.
To determine whether the average grade of the population is significantly more than 75, we can perform a hypothesis test using the given sample data. We'll set up the null and alternative hypotheses as follows:
Null Hypothesis (H 0): The average grade of the population is not significantly more than 75.
Alternative Hypothesis (Ha): The average grade of the population is significantly more than 75.
To conduct the hypothesis test, we can use the t-test since the population variance is unknown. Here, we'll assume the sample is representative and the Central Limit Theorem applies.
To calculate the test statistic for this hypothesis test, we will use the t-distribution since the population standard deviation is unknown. The formula for the t-test statistic is as follows:
t = (sample mean - hypothesized mean) / (sample standard deviation / √(sample size))
Given the information:
Sample mean (x) = 78.6
Hypothesized mean (μ) = 75
Sample standard deviation (s) = √(variance) = √(64) = 8
Sample size (n) = 16
Let's calculate the test statistic using the formula:
t = (78.6 - 75) / (8 / √(16))
t = 3.6 / (8 / 4)
t = 3.6 / 2
t = 1.8
To learn more about Test statistic here; https://brainly.com/question/30458874
#SPJ11
Complete Question:
A random sample of 16 statistics examinations from a large population was taken. The average score in the sample was 78.6 with a variance of 64. We are interested in determining whether the average grade of the population is significantly more than 75. Assume the distribution of the population of grades is normal.
How do you get the test statistic?
jas is 8 years younger than Sandeep 10 years ago their ages total 20 how old are they now
Answers
Answer: Jas is 9, and Sandeep is 11.
Step-by-step explanation: 9 + 11 = 20
Explain why a change from 20 to 40 is a 100% increase, but a change from 40 to 20 is a 50% decrease. Increasing 20 to 40 is the same as increasing 20 by a . So, it is a 100% increase. Decreasing 40 to 20 is the same as decreasing 40 by one-half of . So, it is a 50% decrease.
Answers
Answer:
To find increase/decrease, divide the starting number by the ending number.
40 to 20
20 ÷ 40 = 0.5
0.5 can be represented by 50%.
20 to 40
40 ÷ 20 = 2
2 can be represented by 200%. This is why decreasing 40 to 20 is a 200% increase. In the wording, it says it's a 100% increase. That would be 20 plus 20 times 1 (which is the same as 100%) which is 40.
Please help this is my last try
Answers
Answer: It's A I hope this helps!
Step-by-step explanation:
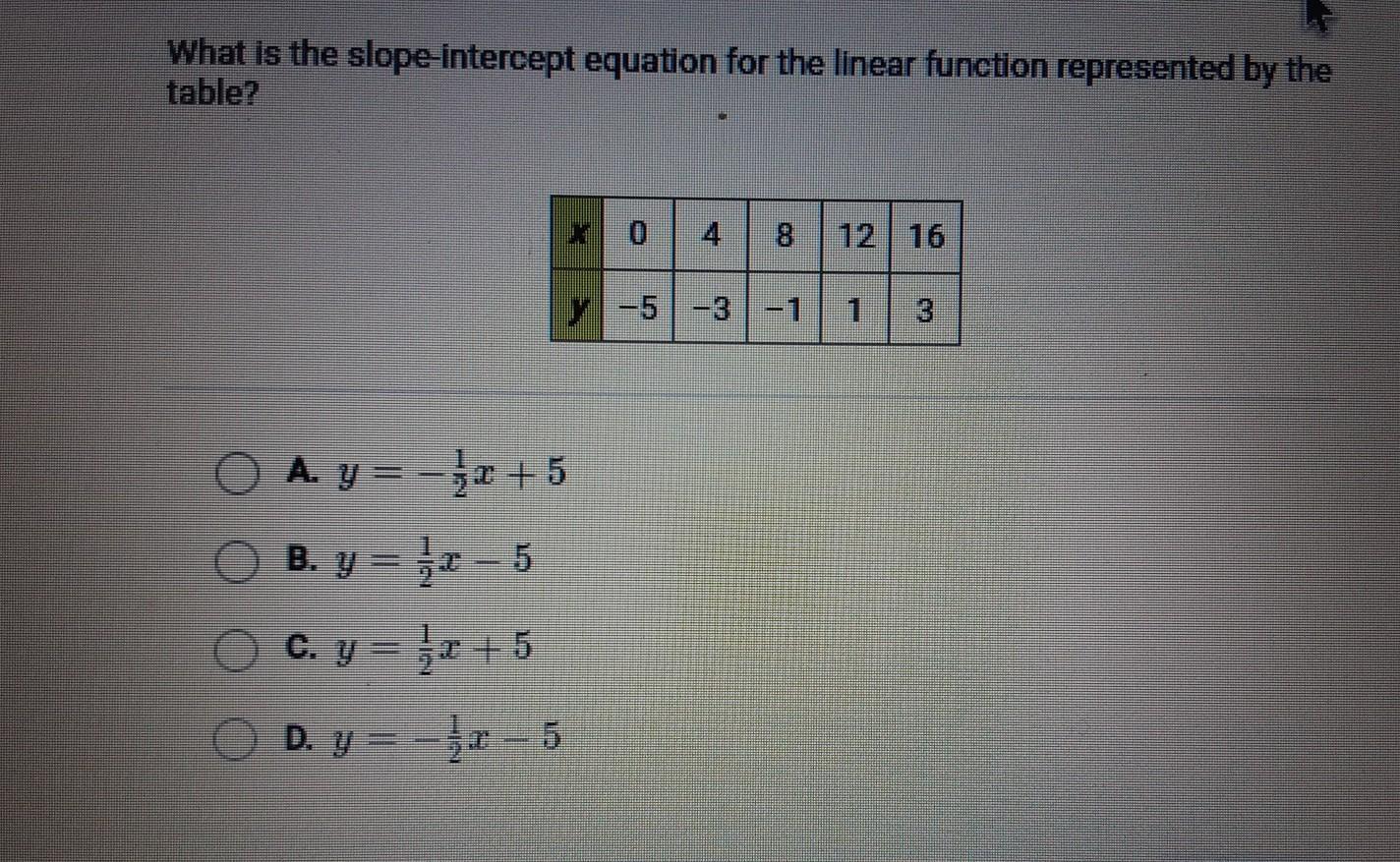
Answer:
y= 1/2x-5
Step-by-step explanation:
Slope intercept equation: y = mx + b
1) find the slope
A (16, 3) B (12,1)
slope = 1/2
2) find b
- we know the slope is 1/2, so...
y = 1/2x+b
substitute the x and y values:
1=1/2(12) + b
1=6+b
b= -5
so, our slope intercept equation is
y = 1/2x - 5
Find the cosine of ZT.
√59
T
√69
U
√10
S
Answers
The cosine of ZT is (√59)/√69.
To find the cosine of ZT, we need to know the values of the adjacent and hypotenuse sides of the right triangle containing angle ZT.
From the given terms, we can see that side TU is the hypotenuse, and side US is the adjacent side. We need to find the length of these sides to determine the cosine of angle ZT.
Using the Pythagorean theorem, we can find the length of side TU:
TU² = TS² + US²
TU² = (√10)² + (√59)²
TU² = 10 + 59
TU² = 69
TU = √69
Now, we can use the definition of cosine to find the value of cos(ZT):
cos(ZT) = adjacent/hypotenuse
cos(ZT) = US/TU
cos(ZT) = (√59)/√69
Therefore, the cosine of ZT is (√59)/√69.
Know more about cosine here:
https://brainly.com/question/24305408
#SPJ11
The mid-points of sides of a triangle are (2, 3), (3, 2) and (4, 3) respectively. Find the vertices of the triangle.
Answers
Answer:
(1, 2), (3, 4), (5, 2)
Step-by-step explanation:
To find the vertices of the triangle given the midpoints of its sides, we can use the midpoint formula:
\(\boxed{\begin{minipage}{7.4 cm}\underline{Midpoint between two points}\\\\Midpoint $=\left(\dfrac{x_2+x_1}{2},\dfrac{y_2+y_1}{2}\right)$\\\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the endpoints.\\\end{minipage}}\)
Let the vertices of the triangle be:
\(A (x_A,y_A)\)\(B (x_B,y_B)\)\(C (x_C, y_C)\)Let the midpoints of the sides of the triangle be:
D (2, 3) = midpoint of AB.E (4, 3) = midpoint of BC.F (3, 2) = midpoint of AC.Since D is the midpoint of AB:
\(\left(\dfrac{x_B+x_A}{2},\dfrac{y_B+y_A}{2}\right)=(2,3)\)
\(\implies \dfrac{x_B+x_A}{2}=2 \qquad\textsf{and}\qquad \dfrac{y_B+y_A}{2}\right)=3\)
\(\implies x_B+x_A=4\qquad\textsf{and}\qquad y_B+y_A=6\)
Since E is the midpoint of BC:
\(\left(\dfrac{x_C+x_B}{2},\dfrac{y_C+y_B}{2}\right)=(4,3)\)
\(\implies \dfrac{x_C+x_B}{2}=4 \qquad\textsf{and}\qquad \dfrac{y_C+y_B}{2}\right)=3\)
\(\implies x_C+x_B=8\qquad\textsf{and}\qquad y_C+y_B=6\)
Since F is the midpoint of AC:
\(\left(\dfrac{x_C+x_A}{2},\dfrac{y_C+y_A}{2}\right)=(3,2)\)
\(\implies \dfrac{x_C+x_A}{2}=3 \qquad\textsf{and}\qquad \dfrac{y_C+y_A}{2}\right)=2\)
\(\implies x_C+x_A=6\qquad\textsf{and}\qquad y_C+y_A=4\)
Add the x-value sums together:
\(x_B+x_A+x_C+x_B+x_C+x_A=4+8+6\)
\(2x_A+2x_B+2x_C=18\)
\(x_A+x_B+x_C=9\)
Substitute the x-coordinate sums found using the midpoint formula into the sum equation, and solve for the x-coordinates of the vertices:
\(\textsf{As \;$x_B+x_A=4$, then:}\)
\(x_C+4=9\implies x_C=5\)
\(\textsf{As \;$x_C+x_B=8$, then:}\)
\(x_A+8=9 \implies x_A=1\)
\(\textsf{As \;$x_C+x_A=6$, then:}\)
\(x_B+6=9\implies x_B=3\)
Add the y-value sums together:
\(y_B+y_A+y_C+y_B+y_C+y_A=6+6+4\)
\(2y_A+2y_B+2y_C=16\)
\(y_A+y_B+y_C=8\)
Substitute the y-coordinate sums found using the midpoint formula into the sum equation, and solve for the y-coordinates of the vertices:
\(\textsf{As \;$y_B+y_A=6$, then:}\)
\(y_C+6=8\implies y_C=2\)
\(\textsf{As \;$y_C+y_B=6$, then:}\)
\(y_A+6=8 \implies y_A=2\)
\(\textsf{As \;$y_C+y_A=4$, then:}\)
\(y_B+4=8\implies y_B=4\)
Therefore, the coordinates of the vertices A, B and C are:
A (1, 2)B (3, 3)C (5, 2)
Find the volume of the prism.

Answers
Answer:
238m^3
Step-by-step explanation:
Volume = lwh (length times width times height)
so do 4 x 7 x 8 1/2
this gets you 238m^3 (because you have to cube your answer with units)
f(x,y)=−4x2+4xy−2y2+6x+8y Suppose that there is a constraint such that xy≤15, What is the value of y that optimizes the function? Question 17 f(x,y)=−4x2+4xy−2y2+6x+8y Suppose that there is a constraint such that xy≤15, what is the Lagrange Multiplier?
Answers
The value of y that optimizes the function is y = 3/2. The Lagrange Multiplier in this case is -105/8.
To optimize the function \(f(x, y) = -4x^2 + 4xy - 2y^2 + 6x + 8y\) subject to the constraint xy ≤ 15, we can use the method of Lagrange multipliers.
The Lagrangian function is defined as:
L(x, y, λ) = f(x, y) - λ(g(x, y) - 15)
where g(x, y) = xy is the constraint equation.
To find the optimal value of y, we need to solve the following system of equations:
∂L/∂x = -8x + 4y + 6 - λy = 0 (1)
∂L/∂y = 4x - 4y + 8 - λx = 0 (2)
g(x, y) - 15 = xy - 15 = 0 (3)
From equation (1), we can rearrange it as:
-8x + 4y - λy = -6 (4)
From equation (2), we can rearrange it as:
4x - 4y - λx = -8 (5)
To solve this system of equations, we can eliminate λ by multiplying equation (4) by x and equation (5) by y, and then subtracting the resulting equations:
\(-8x^2 + 4xy - λxy = -6x (6)\\4xy - 4y^2 - λxy = -8y (7)\)
Subtracting equation (7) from equation (6), we get:
\(-8x^2 + 4xy - 4y^2 = -6x + 8y\)
Simplifying this equation gives:
\(-8x^2 - 4y^2 + 4xy = -6x + 8y\)
Rearranging terms, we have:
\(-8x^2 + 4xy + 6x - 4y^2 - 8y = 0\)
Factoring, we get:
(2x - y)(-4x - 2y + 6) = 0
Setting each factor equal to zero gives:
2x - y = 0 (8)
-4x - 2y + 6 = 0 (9)
From equation (8), we can solve for y:
y = 2x (10)
Substituting equation (10) into equation (9), we get:
-4x - 4x + 6 = 0
Simplifying, we have:
-8x + 6 = 0
Solving for x, we find:
x = 3/4
Substituting this value of x into equation (10), we can find y:
y = 2 * (3/4) = 3/2
Therefore, the value of y that optimizes the function is y = 3/2.
To find the Lagrange Multiplier, we substitute the optimal values of x and y into the constraint equation (3):
xy - 15 = (3/4) * (3/2) - 15 = 9/8 - 15 = -105/8
Hence, the Lagrange Multiplier is -105/8.
To know more about Lagrange Multiplier,
https://brainly.com/question/32575503
#SPJ11
Question 1-
A scatter plot is shown on the coordinate plane.
Which two points would a line of fit go through to best fit the data?
A. (1,9) and (9,5)
B. (1,9) and (5,7)
C. (2,7) and (4,3)
D. (2,7) and (6,5)
Question 2-
Laila participated in a dance-a-thon charity event to raise money for the Animals are Loved Shelter. The graph shows the relationship between the number of hours Laila danced, x, and the money she raised, y.
Determine the slope and explain its meaning in terms of the real-world scenario.
A. The slope is 1/4, which means that the amount of the student raised increases by $0.75 each hour.
B. The slope is 4, which means that the amount the student raised increases by $4 each hour.
C. The slope is 12, which means that the student will finish raising money after 12 hours.
D. The slope is 20, which means that the student started with $20.

Answers
Question 1-
To determine which two points would a line of fit go through to best fit the data on the scatter plot, we need to visually analyze the pattern of the data points and choose two points that the line would pass through to represent the overall trend.
Without the actual scatter plot provided, I am unable to directly analyze it. However, based on the given answer choices:
A. (1,9) and (9,5)
B. (1,9) and (5,7)
C. (2,7) and (4,3)
D. (2,7) and (6,5)
Since I don't have the scatter plot, I cannot accurately determine which points would best fit the data. I would recommend carefully reviewing the scatter plot and selecting the two points that seem to represent the general trend or pattern of the data. The two points that form a line that closely follows the general direction of the data points would be the best choices.
Question 2-
To determine the slope of the relationship between the number of hours Laila danced, x, and the money she raised, y, we need to examine the graph and calculate the slope using the formula:
Slope = (change in y) / (change in x)
However, since the graph is not provided, it is not possible to directly calculate the slope. However, we can still evaluate the given answer choices based on their explanations:
A. The slope is 1/4, which means that the amount the student raised increases by $0.75 each hour.
B. The slope is 4, which means that the amount the student raised increases by $4 each hour.
C. The slope is 12, which means that the student will finish raising money after 12 hours.
D. The slope is 20, which means that the student started with $20.
From the explanations provided, it seems that option B would be the most reasonable choice. A slope of 4 would indicate that for each additional hour Laila danced, she raised $4. However, without the actual graph, it is challenging to confirm the accuracy of the answer choice or its real-world interpretation.
If anyone can help me with this problem!! I would greatly appreciate it.

Answers
AB and YX are corresponding sides, BC and XZ are corresponding sides, and AC and YZ are corresponding sides of given triangle.
What is triangle?
A triangle is a two-dimensional geometric shape that has three sides, three angles, and three vertices. It is one of the simplest polygonal shapes and is commonly studied in geometry.
Since we have:
∠A ≅ ∠Y
∠B ≅ ∠X
∠C ≅ ∠Z
We can conclude that the two triangles ABC and XYZ are similar by the Angle-Angle (AA) similarity theorem.
Therefore, the corresponding sides of the two triangles are proportional to each other. We can write this as:
AB : YX = BC : XZ = AC : YZ
where AB and YX are corresponding sides, BC and XZ are corresponding sides, and AC and YZ are corresponding sides.
In other words, the ratio of the length of each side in triangle ABC to the corresponding side in triangle XYZ is constant.
To learn more about triangle visit:
https://brainly.com/question/1058720
#SPJ9
one mile is equal to 5280 feet
Answers
Length of the golf club where Bruce plays = 7,040 yards
Solution:
1. Let's convert 7,040 yards to miles:
1 yard = 0.000568182 mile
Now, we can use Direct Rule of Three, as follows:
Yards Miles
1 0.000568182
7,040 x
2. Solve for x:
1 * x = 0.000568182 * 7,040
x = 4 miles
What is the probability of flipping 3
coins and having exactly two of them
land on tails?
Answers
Step-by-step explanation:
We can also simply calculate the total number of possible outcomes of 3 coin flips, meaning the overall probability of exactly 2 coin flips out of 3 being tails is 37.5%.
ASAP PLEASE HELP IF RIGHT ANSWER WILL GIVE BRAINLIEST, 15 POINTS, AND 5 STAR OVERALL!!!! IF WRONG ANSWER OR INVALID WILL REPORT, PLEASE, PLEASE, PLEASE!!

Answers
The inequality that is represented by the given graph is; y ≤ (3/4)x - 2
How to Interpret Inequality Graphs?
From the given inequality graph, we see that;
Slope; m = 3/4
x-intercept = -2.5
y-intercept = -2
Now, the equation of a line in slope intercept form is;
y = mx + c
where;
m is slope
c is y-intercept
Thus, our graph is ordinarily;
y = (3/4)x + (-2)
y = (3/4)x - 2
However, it is an inequality that is shaded at the bottom with a thick line and so the inequality becomes;
y ≤ (3/4)x - 2
Read more about Inequality Graphs at; https://brainly.com/question/11234618
#SPJ1
Let f: R → R be a function. Show that: f one-to-one => f not even (Hint: try contrapositive or contradiction)
Answers
To begin with, let's recall the definition of a one-to-one function. A function f: A → B is one-to-one if every element in A is mapped to a unique element in B. In other words, no two distinct elements in A are mapped to the same element in B.
Now, let's assume that f is one-to-one and even. This means that f(-x) = f(x) for all x in R. To prove that f cannot be both one-to-one and even, we will use a proof by contradiction. Suppose f is both one-to-one and even. Then, for any x and y in R, if f(x) = f(y), we must have x = y. Now, let's consider the case when x and y are negative numbers such that x ≠ y. Since f is even, we have f(-x) = f(x) and f(-y) = f(y). However, since f is one-to-one, we cannot have f(-x) = f(-y) because x and y are distinct.Therefore, f cannot be both one-to-one and even. Alternatively, we could use the contrapositive of the statement. The contrapositive of "f one-to-one => f not even" is "f even => f not one-to-one". This means that if f is even, then it cannot be one-to-one. This is true because, as we showed earlier, if f is even, there exist distinct negative numbers that are mapped to the same value, which violates the one-to-one property. In conclusion, we have shown that if a function f is one-to-one, then it cannot be even, using either a proof by contradiction or the contrapositive of the statement.
learn more about Contrapositive here :
https://brainly.com/question/5306301
#SPJ11
(a) Develop a first-order method for approximating f" (1) which uses the data f (x - 2h), f (x) and f (x + 3h). (b) Use the three-point centred difference formula for the second derivative to ap- proximate f" (1), where f (x) = 1-5, for h = 0.1, 0.01 and 0.001. Furthermore determine the approximation error. Use an accuracy of 6 decimal digits for the final answers of the derivative values only.
Answers
(a) Using a first-order method, we can approximate f"(1) as:
f"(1) ≈ [f(x-2h) - 2f(x) + f(x+3h)] / (5\(h^2\))
(b) The exact value of f"(1) is -1, so the approximation error for each of the above calculations is:
Error = |1.6 - (-1)| ≈ 2.6
(a) Using a first-order method, we can approximate f"(1) as:
f"(1) ≈ [f(x-2h) - 2f(x) + f(x+3h)] / (5\(h^2\))
(b) Using the three-point centered difference formula for the second derivative, we have:
f"(x) ≈ [f(x-h) - 2f(x) + f(x+h)] / \(h^2\)
For f(x) = 1-5 and x = 1, we have:
f(0.9) = 1-4.97 = -3.97
f(1) = 1-5 = -4
f(1.1) = 1-5.03 = -4.03
For h = 0.1, we have:
f"(1) ≈ [-3.97 - 2(-4) + (-4.03)] / (\(0.1^2\)) ≈ 1.6
For h = 0.01, we have:
f"(1) ≈ [-3.997 - 2(-4) + (-4.003)] / (\(0.01^2\)) ≈ 1.6
For h = 0.001, we have:
f"(1) ≈ [-3.9997 - 2(-4) + (-4.0003)] / (0.00\(1^2\)) ≈ 1.6
The exact value of f"(1) is -1, so the approximation error for each of the above calculations is:
Error = |1.6 - (-1)| ≈ 2.6
Therefore, the first-order method and three-point centered difference formula provide an approximation to f"(1), but the approximation error is relatively large.
For more such answers on the first-order method
https://brainly.com/question/31402376
#SPJ11
we are asked to develop a first-order method for approximating the second derivative of a function f(1), using data points f(x-2h), f(x), and f(x+3h). A first-order method uses only one term in the approximation formula, which in this case is the point-centred difference formula.
This formula uses three data points and approximates the derivative using the difference between the central point and its neighboring points. For part (b) of the question, we are asked to use the three-point centred difference formula to approximate the second derivative of a function f(x)=1-5, for different values of h. The approximation error is the difference between the true value of the derivative and its approximation, and it gives us an idea of how accurate our approximation is. (a) To develop a first-order method for approximating f''(1) using the data f(x-2h), f(x), and f(x+3h), we can use finite differences. The formula can be derived as follows: f''(1) ≈ (f(1-2h) - 2f(1) + f(1+3h))/(h^2) (b) For f(x) = 1-5x, the second derivative f''(x) is a constant -10. Using the three-point centered difference formula for the second derivative: f''(x) ≈ (f(x-h) - 2f(x) + f(x+h))/(h^2) For h = 0.1, 0.01, and 0.001, calculate f''(1) using the formula above, and then determine the approximation error by comparing with the exact value of -10. Note that the approximation error is expected to decrease as h decreases, and the final answers for derivative values should be reported to 6 decimal digits.
Learn more about first-order method here: brainly.com/question/16292276
#SPJ11
A rectangle has an area of 56x2y units2. If the height of the rectangle is 7xy. What is the length of the rectangle.
Answers
Answer:
8x units
Step-by-step explanation:
A rectangle has an area of 56x²y units². If the height of the rectangle is 7xy. What is the length of the rectangle.
The Area of a Rectangle is calculated with the formula
Length × Width ( Height)
Area = 56x²y square units
Height = 7xy units
Length =Area of the rectangle/Height of the rectangle
= 56x²y square units/7xy units
= 8x units
I NEED HELP ON THIS ASAP, IT'S DUE TODAY!

Answers
The inequalities which the number lines represent are as follows;
x > 3
x <= 2.
What are inequalities ?A mathematical comparison and expression of the relationship between two expressions is known as an inequality.
It can be seen as a generalization of an equation and is denoted by a symbol like ">", "", "", or "".
In contrast to an equation, which only has one solution, an inequality may have several answers or none at all.
The values that give rise to an inequity are its remedies.
The range of potential values for a variable is one example of how inequality models limits or limitations in the real world.
They can also be used to describe how two variables relate to one another, such as when one is more than or less than the other.
According to our question-
the inequality is; x <= 2
the inequality is; x > 3
x > 3
x <= 2
learn more about inequalities click here:
https://brainly.com/question/30238989
#SPJ1
I don’t understand #6 question

Answers
Answer:
B. (10, 2000)
Step-by-step explanation:
5000 - 300t = 1400ft - 1200f
=> t = 10
10 => (5000 - 300t) = 2000
So the answer is B. (10, 2000)
HOPE THIS HELPS AND HAVE A NICE DAY <3
Given: AD diameter of Circle P. If m 1 = 40°, then m AB = A)80 B)40 C)20
Answers
Answer:
20
Step-by-step explanation:
lol
Answer:
20
Step-by-step explanation:
Calculate the slope of the line.Please help!!

Answers
Struggling with this… please help

Answers
B = 47°
a = 10.9
b = 11.7
How are the angles and sides of the right triangle calculated?
a) Finding B
We know that ,the sum of every angles of a triangle = 180°
So, B + 90° +43° = 180°
B+ 133° = 180°
B = 180° - 133°
=47°
b) Finding a
We know,
\(sin\theta =\frac{opposite}{hypotenuse} \\\\sin 43^{\circ} =\frac{a}{16} \\\\a= 16(sin 43^{\circ})\\\\a = 16 (0.681)\\\\a=10.9\)
c) Finding b
We know,
\(cos\theta = \frac{adjacent}{hypotenuse} \\\\cos 43^{\circ} =\frac{b}{16} \\\\b = (cos 43^{\circ})16\\\\b= (0.731) 16\\\\b= 11.7\)
What is a right triangle?
A triangle with a right angle or two perpendicular sides is referred to as a right triangle, right-angled triangle, or orthogonal triangle . Trigonometry's foundation is the relationship between the right triangle's sides and other angles. A right triangle's hypotenuse is always the side that faces away from the right angle. It is the right triangle's longest side. From a particular angle, the opposite side is across. The non-hypotenuse side next to a specific angle is referred to as the adjacent side.To learn more about right triangle, refer:
https://brainly.com/question/15739772
#SPJ13
An algorithm will be used to count how many numbers in a list are multiples of either 5 or 10. For the list of [5, 3, 2, 10, 20, 7], it should count 3 numbers (5, 10, 20). There are two proposals for the algorithm: Algorithm 1: Set value of count to 0. Iterate through each number in the list. If the current number is a multiple of 5 and a multiple of 10, increment count by 1. Algorithm 2: Set value of count to 0. Iterate through each number in the list. If the current number is a multiple of 5, increment count by 1. Then, if the current number is a multiple of 10, increment count by 1.
Answers
Algorithm 2 is the better proposal for this problem.
The reason for this is because of the specific nature of the problem statement.
The prompt calls for a count of the numbers that are multiples of either 5 or 10. However, Algorithm 1 only counts the numbers that are multiples of both 5 and 10.
This means that Algorithm 1 will not capture all the relevant numbers in the list, thus leading to incorrect results.
On the other hand, Algorithm 2 correctly counts all the numbers that are multiples of either 5 or 10. This is because it checks for multiples of 5 first and increments count if it finds a multiple.
Then, it checks for multiples of 10 and increments count again if it finds a multiple. By doing this, Algorithm 2 correctly captures all the relevant numbers in the list, thus leading to correct results.
Overall, Algorithm 2 is the better proposal for this problem.
To learn about algorithms here:
https://brainly.com/question/24953880
#SPJ11
Plz help I made it extra points...

Answers
Answer:
a is a linear equation
Step-by-step explanation:
NEED HELP ASAP! WILL MARK BRAINLIST

Answers
Answer:
B
Step-by-step explanation:
cut tghe shape into one rectangle and a two cimi circles
area of a rect. is b x h --> 7x14 = 98ft^2
now make the two cimi circles a whoal and find the area of a circle
pie r^2 --> 3.14x3.5^2 = 38.48
add both getting about 136.48
Answer:
136.48 ft^2 (B)
Step-by-step explanation:
First, we need to find the area of a rectangle.
A(rectangle) = l * w
= 14 ft * 7 ft
= 98 ft^2
Next we need to find the area of the two semicircles.
A(semicircle) * 2 = πr^2/2 * 2
= π(3.5 ft)^2
= 12.25π ft^2
= 38.48 ft^2
Finally, you add the two areas:
98 ft^2 + 38.48 ft^2 = 136.48 ft^2
Hope this helps!
According to the similarity–attraction hypothesis, given a greater perception of similarity between two individuals from different cultures, what is likely to happen?
Answers
According to the similarity-attraction hypothesis, when two individuals from different cultures perceive a greater similarity between themselves, it is likely that they will experience increased attraction towards each other.
This means that the perception of shared characteristics, values, and beliefs between individuals can lead to a stronger sense of connection and positive feelings. It is important to note that this hypothesis suggests perceived similarity and attraction, but it does not guarantee the formation of relationships or friendships.
Hypothesis https://brainly.com/question/31362172
#SPJ11