t^12 x t^5 and i need the anser
Answers
Answer: t^17
Step-by-step explanation:
Answer:
t^17
Step-by-step explanation:
if you're going to multiply, you're just gonna add the exponent.
Related Questions
Can a triangle have the sides 5'7 12?
Answers
It is not possible to construct a triangle whose sides are 5 cm 7 cm and 12 cm because the sum of two sides(5 cm and 7 cm) are equal to the third sides(12 cm). Two equal sides cannot form a triangle.
In the given question, we have to check that it is possible to construct a triangle whose sides are 5 cm 7 cm and 12 cm.
The sum of the two sides must always be greater than the third side in order to determine whether or not the given sides may form a triangle.
To check this we firstly add the 5 and 7.
7 + 5 = 12
12 = 12
Now we add 5 and 12
5 + 12 > 7
17 > 7
Now we add 7 and 12
7 + 12 > 5
19 > 5
It is not possible to construct a triangle whose sides are 5 cm 7 cm and 12 cm because the sum of two sides(5 cm and 7 cm) are equal to the third sides(12 cm). Two equal sides cannot form a triangle.
To learn more about construct a triangle link is here
brainly.com/question/26784196
#SPJ4
The complete question is:
Can a triangle have the sides 5 cm 7 cm and 12 cm?
2. Please use the earliest deadline first scheduling algorithm to construct a schedule (1.e.. execution sequence) of the following task set: T1 = {2ns, Sns, Sns), Tz = {4ns, 7ns, 7ns} during a period of 22 ns. Here the notation Ti = {eu Pi, D} gives the execution time e; period P. and deadline of task t (20 points)
Answers
The schedule is as follows:
T1 -> T2 -> T1 -> T3 -> T1 -> T2 -> T1.
To construct a schedule using the Earliest Deadline First (EDF) scheduling algorithm, we need to consider the execution time, period, and deadline of each task and assign them priorities based on their deadlines. The task with the earliest deadline will be scheduled first. Let's create a schedule for the given task set:
Task T1: Execution time (e) = 2 ns, Period (P) = 5 ns, Deadline (D) = 5 ns
Task T2: Execution time (e) = 4 ns, Period (P) = 7 ns, Deadline (D) = 7 ns
Task T3: Execution time (e) = 7 ns, Period (P) = 7 ns, Deadline (D) = 7 ns
We have a period of 22 ns, and we need to schedule these tasks within that period. Let's start with the task with the earliest deadline:
At time 0 ns: Execute T1 (2 ns)
At time 2 ns: Execute T2 (4 ns)
At time 6 ns: Execute T1 (2 ns)
At time 8 ns: Execute T3 (7 ns)
At time 15 ns: Execute T1 (2 ns)
At time 17 ns: Execute T2 (4 ns)
At time 21 ns: Execute T1 (2 ns)
This completes the execution of all tasks within the given period of 22 ns. The schedule is as follows:
T1 -> T2 -> T1 -> T3 -> T1 -> T2 -> T1
In this schedule, we have followed the EDF algorithm by selecting tasks based on their deadlines. The task with the earliest deadline is always scheduled first to meet the timing requirements of the system.
To learn more about EDF algorithm, click here: brainly.com/question/28501187
#SPJ11
Given the information in the picture about triangle GTR, explain how you can determine if side RT is tangent to the circle
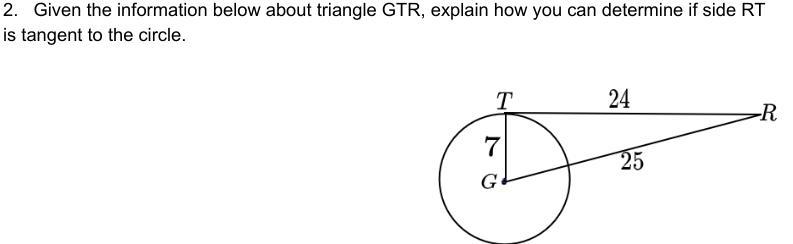
Answers
If RT has a length of approximately 22.97 units, then it is a tangent to the circle. Otherwise, it is not a tangent to the circle.
What is tangent?A tangent is a straight line or plane that touches a curved surface at a single point without intersecting it at that point.
Let O be the center of the circle and let M be the midpoint of the line segment RT. Since GT is a radius of the circle, we have GM = GT/2 = 7/2.
Since the line segment from the center O to R forms a right angle with RT (by the definition of a tangent), the triangle GTR is a right triangle with hypotenuse GR and legs GM and MR.
Using the Pythagorean theorem, we have:
GR² = GM² + MR²
Substituting the given values, we have:
GR² = (7/2)² + (RT/2)²
Simplifying, we have:
GR² = 49/4 + RT²/⁴
Since GR is the radius of the circle and is therefore a constant, we can conclude that RT is a tangent to the circle if and only if GR^2 = 24^2, or:
49/4 + RT²/⁴ = 24²
Solving for RT, we have:
RT² = 24² - 49
RT²= 527
RT ≈ 22.97
To know more about line segment visit:
https://brainly.com/question/10496716
#SPJ1
3 question someone help me also each of the question be will 100 points if you answered.

Answers
Answer:
division is required on left side
Step-by-step explanation:
24 _ - \(\frac{3}{4}\)
consider 24 ÷ - \(\frac{3}{4}\)
change division to multiplication and turn fraction upside down
= 24 × - \(\frac{4}{3}\)
= 8 × - 4
= - 32 ← equals value on right side
use a graph to solve each equation.
1. 4x + 6 = 8x - 10
2. -3/4x - 2 = -1/2x + 1
3. |4-2x| + 5 = 9
Use a graph to solve each inequality:
4. x^2 + 4x - 5 < 0
5. x^2 - x - 12 ≥ 0
Answers
The solutions to the equations are
1. x = 4
2. x = -12
3. x = 0 and x = 4
The solutions to the inequalities are
4. -5 < x < 1
5. x ≤ -3 and x ≥ 4
How to solve the equations using graphsFrom the question, we have the following equations
1. 4x + 6 = 8x - 10
2. -3/4x - 2 = -1/2x + 1
3. |4 - 2x| + 5 = 9
Next, we split the equations to 2
So, we have
1. y = 4x + 6 and y = 8x - 10
2. y = -3/4x - 2 and y = -1/2x + 1
3. y = |4 - 2x| + 5 and y = 9
Next, we plot the system of equations (see attachment) and write out the solutions
The solutions are
1. x = 4
2. x = -12
3. x = 0 and x = 4
How to solve the inequalities using graphsFrom the question, we have the following inequalities
4. x² + 4x - 5 < 0
5. x² - x - 12 ≥ 0
Next, we plot the system of inequalities (see attachment) and write out the solutions
The solutions are
4. -5 < x < 1
5. x ≤ -3 and x ≥ 4
Read more about equations at
https://brainly.com/question/148035
#SPJ4

Gabe goes to the mall. If k is the number of items he bought, the expression 18.58k+30 gives the amount he spent in dollars at one store. Then he spent 22 dollars at another store. Find the expression which represents the amount Gabe spent at the mall. Then estimate how much Gabe spent if he bought 3 items.
Answers
The expression which represents the amount Gabe spent at the mall will be 18.58k + 52.
The amount that Gabe spent if he bought 3 items will be $107.74.
How to calculate the expression?From the information, Gabe goes to the mall. If k is the number of items he bought, the expression 18.58k+30 gives the amount he spent in dollars at one store and he spent 22 dollars at another store.
The expression which represents the amount Gabe spent at the mall will be:
= 18.58k + 30 + 22
= 18.58k + 52
The amount that Gabe spent if he bought 3 items will be:
= 18.58k + 52
= 18.58(3) + 52
= $107.74
Learn more about expressions on
brainly.com/question/723406
#SPJ1
Two bumper cars are driven straight toward
each other. The mass of bumper car 1 is
110.0 kg, and the mass of bumper car 2 is
170.0 kg.
Bumper car 1 has a velocity of 1.5 m/s and bumper car 2 has a velocity of -2.0 m/s.
The final velocity of bumper car 1 is -2.75 m/s
What is the velocity of bumper car 2 immediately after the collision?
Answers
By conservation of momentum,
(110.0 kg) (1.5 ms⁻¹) + (170.0 kg) (-2.0 ms⁻¹) = (110.0 kg) (-2.75 ms⁻¹) + (170.0 kg) v
where v is the final velocity of the second car.
Solve for v :
-175 kg•ms⁻¹ = -302.5 kg•ms⁻¹ + (170.0 kg) v
127.5 kg•ms⁻¹ = (170.0 kg) v
v = (127.5 kg•ms⁻¹) / (170.0 kg) = 0.75 ms⁻¹
Help help me pleaseee and thanks

Answers
Answer:
10
Step-by-step explanation:
sqrt. 100 = 10
because base x height = area
base and height must be same length in a square
Quickly
Triangle XYZ- triangle JKL. Use the image to answer the question.
K to j is10.44
K to L = unknown
L to J = 9.84
X to Y = 8.7
X to Z = 8.2
Y to Z = 7.8
Determine the measurement of KL.
A: KL = 8.58
B: KL = 6.36
Answers
The value of KL as shown in the image is 12 units
What is an equation?An equation is an expression that shows how numbers and variables using mathematical operators.
Two triangles are said to be similar, if the ratio of their corresponding sides are in the same proportion.
For the triangle shown, since triangle XYZ is similar to triangle JKL, hence:
KL/XY = KJ / XZ
substituting, KJ = 10.44:
KL / 8.7 = 11.31 / 8.2
KL = 12
The value of KL is 12 units
Find out more on equation at: https://brainly.com/question/22688504
#SPJ1

Complete the conversion 2.5 T Lb

Answers
Answer:
2.5 Tons to lb
1 ton = 2,000 lb
2.5 tons x 2000 lb = 5,000 lb
15/53
1
35%
White shapes and black shapes are used in a game.
Some of the shapes are circles.
All the other shapes are squares.
OD
The ratio of the number of white shapes to the number of black shapes is 5:11
The ratio of the number of white circles to the number of white squares is 3:7
The ratio of the number of black circles to the number of black squares is 3:8
Work out what fraction of all the shapes are circles
Answers
9/32 is fraction of all the shapes are circles .
What does a math ratio mean?
An ordered pair of numbers a and b, represented as a / b, is a ratio if b is not equal to 0. A proportion is an equation that sets two ratios at the same value. For instance, you could express the ratio as follows: 1: 3 if there is 1 boy and 3 girls (for every one boy there are 3 girls)Find the equivalent ratio for the total shapes:
Total Black Shapes : Total White Shapes = 5 : 11
Multiply by 2:
Total Black Shapes: Total White Shapes = 10 : 22
Find the ratio for the white shapes:
White circles : White squares = 3 : 7
Sum of the units = 3 + 7
Sum of the units = 10
Find the equivalent ratio for the total shapes:
Black circles : Black squares = 3 : 8
Multiply by 2:
Black circles : Black squares = 6 : 16
Sum of the units = 6 + 16
Sum of the units = 22
Combine the ratios:
white circles : white squares : black circles : black square = 3 : 7 : 6 : 16
Circles = 3 + 6
Circles = 9 units
Total = 3 + 7 + 6 + 16
Total = 32 units
Find the fraction of all the shapes that are circles:
Fraction = 9/32
Learn more about ratio
brainly.com/question/13419413
#SPJ9
help me, please
-31.5 = -6b, b = ?
Answers
Answer:
b=5.25
Step-by-step explanation:
Divide both sides. by -6.
-31.5/-6 = 5.25
b= 5.25
Will give brainly if you can Match the exponential graphs to the situations below in which the investmentslose money.$100 at 8% loss per year$200 at 10% loss per year$100 at 10% loss per year$200 at 8% loss per year1st graph (1,180)2nd graph (1,181)3rd graph (1,92)4th (1,90)

Answers
a)The formula for the graph of $100 at 8% loss per year will be:
\(f(x)=a(1-ppercent)^x\)So the first graph function is:
\(f(x)=100(1-0.08)^x=100(0.92)^x\)The graph is shown below:The
The point (1,92) lies on this graph.
b) The second graph of $200 at 10% loss per year is given by the equation:
\(g(x)=200(1-0.1)^x=200(0.9)^x\)The graph is shown below:
As seen the point (1,180) lies on second graph.
c) The equation for $100 at 10% loss per year is:
\(h(x)=100(1-0.1)^x=100(0.9)^x\)The graph is shown below:
The point (1,90) lies on this graph.
d) The equation for $200 at 8% loss per year is given by:
\(i(x)=200(1-0.08)^x=200(0.92)^x\)The graph is shown below:
As seen the point (1,184) lies on the graph.
So:
$100 at 8% loss per year has the point (1,92).
$200 at 10% loss per year has the point (1,180).
$100 at 10% loss per year has the point (1,90).
$200 at 8% loss per year has the point (1,184)




what is one fifth of 200?
Answers
Answer:
1/5 x 200=40
Step-by-step explanation:
Answer:
1/5*200=40
Step-by-step explanation:
-4x+7y=3
x intercept and y intercept
(,) (,)

Answers
rAnswer: x-intercept: (-0.75, 0)
y-intercept: (0, 3/7)
Step-by-step explanation: An x and y intercept is the point when the line crosses the x and y axis respectively. When a line crosses the x axis, the y value is 0 and when the line crosses y axis, the x value is 0. This means we can set y and x equal to 0 and solve for the other variable.
To solve for the x intercept, we set y equal 0 so:
-4x + 7(0) = 3
-4x = 3
x = -(3/4)
so we get
(-3/4, 0) or (-0.75, 0) for our x int
For the y intercept we set x equal 0:
-4(0) + 7y = 3
7y = 3
y = 3/7
so we get
(0, 3/7) for our y int
Find a vector function r(t), that represents the curve of intersection of the two surfaces. the cylinder x2 y2=36 and the surface z=4xy
Answers
Given:
\(\begin{aligned}&x^2+y^2=16 \\&z=x y\end{aligned}\)
Express 16 as \(4^{2}\): \(x^2+y^2=16\)
\(x^2+y^2=4^2\\x^2+y^2=4^2 \times 1\)
Trignometry,
\(\cos ^2(t)+\sin ^2(t)=1\)
Now, substitute \(\cos ^2(t)+\sin ^2(t)\) for 1:
\(\begin{aligned}&x^2+y^2=4^2 \times 1 \\&x^2+y^2=4^2 \times\left[\cos ^2(t)+\sin ^2(t)\right]\end{aligned}\\x^2+y^2=4^2 \times \cos ^2(t)+4^2 \times \sin ^2(t)\)
Law of indicates:
\(\begin{aligned}&x^2+y^2=[4 \times \cos (t)]^2+[4 \times \sin (t)]^2 \\&x^2+y^2=[4 \cos (t)]^2+[4 \sin (t)]^2\end{aligned}\\x^2=[4 \cos (t)]^2 \text { and } y^2=[4 \sin (t)]^2\)
Taking positive square roots as follows:
\(x=4 \cos (t), y=4 \sin (t)\)
Recall that, z = xy.
Now, we have:
\(\begin{aligned}&z=4 \cos (t) \times 4 \sin (t) \\&z=16 \cos (t) \cdot \sin (t)\end{aligned}\)
Now, substitute the values:
\(r(t)=x_t i+y_t j+z_t k\)
So, the vector r(t) is: \(r(t)=(4 \cos (t)) i+(4 \sin (t)) i+(16 \cos (t) \cdot \sin (t)) i\)
Therefore, the vector function r(t) is written as: \(r(t)=x_t i+y_t j+z_t k\)
Know more about vector functions here:
https://brainly.com/question/14895420
#SPJ4
find the missing value of y that makes the equation y=2/3x-4 true when x=9
Answers
Answer: true when x = 9 is y = 2.
Step-by-step explanation:
To find the missing value of y that makes the equation y = (2/3)x - 4 true when x = 9, we substitute x = 9 into the equation and solve for y.
Substituting x = 9 into the equation:
y = (2/3)(9) - 4
Simplifying the equation:
y = 6 - 4
y = 2
Therefore, the missing value of y that makes the equation true when x = 9 is y = 2.
Use the pythagorean theorem to find ad and dc. then find ac using addition. show your calculations.
Answers
The length of AC, the hypotenuse in the right triangle ABC, is 5 units.
Correct answer is AC= 5 .
To find the length of AC in a right triangle ABC, we can use the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (AC) is equal to the sum of the squares of the lengths of the other two sides (AD and DC).
Given that AD = 3 and DC = 4, we can calculate AC as follows:
Step 1: Square the lengths of AD and DC:
AD^2 = 3^2 = 9
DC^2 = 4^2 = 16
Step 2: Add the squares of AD and DC:
AD^2 + DC^2 = 9 + 16 = 25
Step 3: Take the square root of the sum to find the length of AC:
AC = √25 = 5
Therefore, the length of AC is 5 units.
In conclusion, the length of AC, the hypotenuse in the right triangle ABC, is 5 units.
For more questions on right triangle
https://brainly.com/question/1248322
#SPJ8
complete question should be In a right triangle ABC, where AC is the hypotenuse, AD and DC are the two legs. To find the lengths of AD and DC, we can use the Pythagorean theorem. If AD = 3 and DC = 4, what is the length of AC? Show your calculations step by step.
what is 10,000 x 1000,000
Answers
x over 2 plus x over 5 equals 1
Answers
Solution of the given fractional equation x over 2 plus x over 5 equals 1 is 10/7
What is a Fractional equation ?
A fractional equation is one that contains one or more terms that are fractions. The first step in solving a fractional equation is to remove the fractions by multiplying both sides of the equation by the LCD of each term. We are able to accomplish this because an equation does not get out of balance when both sides are multiplied by the same amount, in this example, the LCD. The fractions are now gone, and the equation may now be solved like any other nonfractional problem.
A fractional equation is one in which one or more of its terms have the unknown as their denominator.
X/2 + X/5 = 1
X(1/2 +1/5)= 1
X(7/10)= 1
X = 10/7
Learn more about Fractional equation from the link below
https://brainly.com/question/20337104
#SPJ1
what is please im stuck on this question y=−3x+21?
Answers
Slope - intercept form is y = mx + b
m = -3
b = 21
slope: 3
y- intercept : ( 0, 21 )

the least squares method for determining the best fit minimizes
Answers
The least squares method minimizes the sum of the squared differences between the observed data points and the predicted values.
The least squares method is a mathematical technique used to find the best fit line or curve for a set of data points. It is commonly used in regression analysis to determine the relationship between two variables.
The method works by minimizing the sum of the squared differences between the observed data points and the predicted values from the line or curve. This sum is known as the residual sum of squares (RSS) or the sum of squared residuals (SSR).
The least squares method aims to find the line or curve that minimizes this sum, meaning it minimizes the overall error between the observed data and the predicted values. By minimizing the sum of squared differences, the method finds the line or curve that best represents the data.
In other words, the least squares method seeks to find the line or curve that provides the best balance between fitting the data closely and avoiding extreme deviations from the data points.
Learn more:About least squares method here:
https://brainly.com/question/31984229
#SPJ11
The least squares method for determining the best fit minimizes the sum of the squared differences between the observed data points and the corresponding values predicted by the mathematical model or regression line.
In other words, it aims to minimize the sum of the squared residuals, where the residual is the difference between the observed data point and the predicted value. By minimizing the sum of squared residuals, the least squares method finds the line or curve that best fits the data by minimizing the overall error between the predicted values and the actual data.
Mathematically, the least squares method minimizes the objective function:
E = Σ(yᵢ - ŷᵢ)²
where yᵢ is the observed value, ŷᵢ is the predicted value, and the summation Σ is taken over all data points. The goal is to find the values of the parameters in the mathematical model that minimize this objective function, usually by differentiating it with respect to the parameters and setting the derivatives equal to zero.
By minimizing the sum of squared differences, the least squares method provides a way to estimate the parameters of a mathematical model that best represents the relationship between the independent and dependent variables in a data set.
About least squares method here:
brainly.com/question/31984229
#SPJ11
You have round tables each seating 6 people. As your guests sit at the table, how many degrees must you rotate to look from the guest to their left to the guest to their right? (Hint: The interior angles of regular polygon measure ((n - 2) x 180) / n where n is the number of sides.)
Answers
To look from the guest to their left to the guest to their right at a round table seating 6 people, you need to rotate by 60 degrees.
For a regular polygon with n sides, the sum of its interior angles is given by ((n - 2) × 180) degrees. In the case of a round table seating 6 people, the table can be considered as a hexagon, which has 6 sides. Using the formula, we can calculate the sum of the interior angles:
((6 - 2) × 180) / 6 = (4 × 180) / 6 = 720 / 6 = 120 degrees
Since the table forms a complete circle, the sum of the interior angles is divided equally among the guests. Therefore, each guest sits at an angle of 120 degrees. To look from the guest to their left to the guest to their right, you need to rotate by the angle between adjacent guests, which is half of the angle they sit at:
120 / 2 = 60 degrees
Thus, to look from the guest to their left to the guest to their right at a round table seating 6 people, you need to rotate by 60 degrees.
Learn more about angle here:
https://brainly.com/question/31818999
#SPJ11
2. Which of the following use the Distributive Property correctly to multiply rational numbers?
A.
3
- 3(-4) + 3
2
B.
2(1) +
:-)--(4-1)-(-4)=(1)
251 (
-(-) ----)--(-946-0(1)
--(23
) --- 2 + 3) --2c97
C.
)+
(
)
4.
D.
() +
E.
3
Answers
Answer: B
Step-by-step explanation: Your answer is b. A graph is drawn. The horizontal axis and vertical axis values are 0 to 15 in increments of 1. The horizontal axis label is Number of Packets, and the vertical axis label is Number of Seeds. Points are plotted on the ordered pairs 1, 3 and 2, 6 and 3, 9.
Good luck!
P.S.
- Amir
You buy a watch for $60. There is a 6% sales tax. What is your total cost for the
watch?
Answers
Answer:
$63.3
Step-by-step explanation:
You buy a 60 dollar watch.
60
There is a 6 percent tax. When adding tax, multiply the 6 percent by the original amount.
60 x 0.06
3.6
Add the tax to the original amount.
60 + 3.6 = 63.3
So, your total cost is 63.3 dollars.
Answer:
$63.60
Step-by-step explanation:
Solve x2 + 12x + 25 = 17 by completing the square. Select all the possible solutions.
A.
6+√7
B. 6+277
C. 6-2/7
D. 6-V7
E 6-287

Answers
Answer:
A,C,D I think.
Step-by-step explanation:
The solution to the quadratic equation is x = -6 ± 2√7
What is Quadratic Equation?A quadratic equation is a second-order polynomial equation in a single variable x , ax² + bx + c=0. with a ≠ 0. Because it is a second-order polynomial equation, the fundamental theorem of algebra guarantees that it has at least one solution. The solution may be real or complex.
The roots of the quadratic equations are
x = [ -b ± √ ( b² - 4ac ) ] / ( 2a )
where ( b² - 4ac ) is the discriminant
when ( b² - 4ac ) is positive, we get two real solutions
when discriminant is zero we get just one real solution (both answers are the same)
when discriminant is negative we get a pair of complex solutions
Given data ,
Let the quadratic equation be represented as A
Now , the value of A is
x² + 12x + 25 = 17
Subtracting 17 on both sides , we get
x² + 12x + 8 = 0
And , roots of the quadratic equations are
x = [ -b ± √ ( b² - 4ac ) ] / ( 2a )
On simplifying , we get
x = ( -12/2 ) ± √ ( 12 )² - 4 ( 1 ) ( 8 ) / 2
x = -6 ± √ ( 144 - 32 ) / 2
x = -6 ± √112/2
And , the value of x = -6 ± 2√28/2
x = -6 ± 2√7
Hence , the solutions are x = -6 + 2√7 and -6 - 2√7
To learn more about quadratic equations click :
https://brainly.com/question/25652857
#SPJ2
18-9.2x10 to the power of -4 subtract the following in.Write your answer in standard notation
Answers
The subtraction of the numbers, involving scientific notation, is given as follows:
18 - 9.2 x 10^(-4) = 17.99908.
What is scientific notation?A number in scientific notation is given according to the rule presented as follows:
\(a \times 10^b\)
The base is \(a \in [1, 10)\), meaning that it can assume values from 1 to 10, with an open interval at 10 meaning that for 10 the number is written as 10 = 1 x 10¹, meaning that the base is 1.
In this problem, we are given the following subtraction:
18 - 9.2 x 10^(-4).
When two numbers are subtracted, they must have the same base, hence we are going to convert 9.2 x 10^(-4) to base 0.
This means that 4 has to be added to the exponent, meaning that the base has to be divided by 10000 to compensate, then:
9.2 x 10^(-4) = 0.00092.
Then the result of the subtraction is given as follows:
18 - 9.2 x 10^(-4) = 18 - 0.00092 = 17.99908.
A similar problem, also about scientific notation, is given at https://brainly.com/question/16394306
#SPJ1
Construct the encryption matrix (as defined in Example Onc-time Pad with n = 3 Example 3.3 Lel P = {a,b} with Prla] = 1/4,Prlb] = 3/ with Pr[Ki] = 1/2, Pr(Kz] Pr[Ks] = 1/4.Let € = {1,2 encryption functions are defined to be eki (a) = 1,eK (6) 3; and eK (a) = 3, CK, (6) = 4 This cryptosystem can be reF ing encryption matrix: Ki 2 Kz 2 3 K3 3
Answers
| | K1 | K2 | K3 | |----|----|----|----| | a | 1 | 3 | 3 | | b | 3 | 4 | 4 | This matrix represents the encryption process of the cryptosystem, where each element in the matrix corresponds to the result of applying the encryption function with a specific key to a specific plaintext character.
The encryption matrix for this cryptosystem can be constructed using the following steps. First, we list the keys used in the system, which are Ki, Kz, and Ks. Then, we list the possible plaintexts, which in this case are a and b. Next, we apply the encryption functions to each key and plaintext combination to obtain the corresponding ciphertexts. Specifically, eKi(a) = 1, eKi(b) = 3, eKz(a) = 3, eKz(b) = 4, eKs(a) = 2, and eKs(b) = 4. Finally, we arrange the ciphertexts in a matrix format, with the rows representing the keys and the columns representing the plaintexts. The resulting encryption matrix is:
| | a | b |
|---|---|---|
| Ki | 1 | 3 |
| Kz | 3 | 4 |
| Ks | 2 | 4 |
This matrix can be used to encrypt a message by selecting a key and then using the corresponding row to encode the plaintext message. For example, if we want to encrypt the message "aba" using the key Kz, we would use the second row of the matrix to obtain the ciphertexts "3 3 4".
To learn more about columns click here
brainly.com/question/29194379
#SPJ11
7 is 12 percent of what number?
Answers
Answer:
12x/100=7
12x=700
x=700/12
x=58.33
From a table of integrals, we know that for ,≠0a,b≠0,
∫cos()=⋅cos()+sin()2+2+.∫eatcos(bt)dt=eat⋅acos(bt)+bsin(bt)a2+b2+C.
Use this antiderivative to compute the following improper integral:
∫[infinity]01cos(3)− = limT→[infinity]∫0[infinity]e1tcos(3t)e−stdt = limT→[infinity] if ≠1s≠1
or
∫[infinity]01cos(3)− = limT→[infinity]∫0[infinity]e1tcos(3t)e−stdt = limT→[infinity] if =1.s=1. help (formulas)
For which values of s do the limits above exist? In other words, what is the domain of the Laplace transform of 1cos(3)e1tcos(3t)?
help (inequalities)
Evaluate the existing limit to compute the Laplace transform of 1cos(3)e1tcos(3t) on the domain you determined in the previous part:
()=L{e^1t cos(3)}=
Answers
"From a table of integrals, we know that for \(\(a \neq 0\)\) and \(\(b \neq 0\):\)
\(\[\int \cos(at) \, dt = \frac{1}{a} \cdot \cos(at) + \frac{1}{b} \cdot \sin(bt) + C\]\)
and
\(\[\int e^a t \cos(bt) \, dt = \frac{e^{at}}{a} \cdot \cos(bt) + \frac{b}{a^2 + b^2} \cdot \sin(bt) + C\]\)
Use this antiderivative to compute the following improper integral:
\(\[\int_{-\infty}^{0} \cos(3t) \, dt = \lim_{{T \to \infty}} \int_{0}^{T} e^t \cos(3t) \, e^{-st} \, dt = \lim_{{T \to \infty}} \text{ if } s \neq 1, \, \text{ or } \lim_{{T \to \infty}} \text{ if } s = 1.\]\)
For which values of \(\(s\)\) do the limits above exist? In other words, what is the domain of the Laplace transform of \(\(\frac{1}{\cos(3)} \cdot e^t \cos(3t)\)\)?
Evaluate the existing limit to compute the Laplace transform of on the domain you determined in the previous part:
\(\[L\{e^t \cos(3t)\\).
To know more about antiderivative visit-
brainly.com/question/9700015
#SPJ11