Tell one the lines for the given points are parallel, perpendicular, or neither. Just your answer.
Line 1: (2, -3), (-4, -6)
Line 2: (-3, 2), (2, -8)
Answers
Answer:
Perpendicular
Step-by-step explanation:
Given
\(Line\ 1: (2, -3), (-4, -6)\)
\(Line\ 2: (-3, 2), (2, -8)\)
Required
Tell the relationship between both lines
We start by calculating the slopes (m) of both lines.
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
For Line 1:
\(m_1 = \frac{-6 - (-3)}{-4 - 2}\)
\(m_1 = \frac{-6 +3}{-4 - 2}\)
\(m_1 = \frac{-3}{-6}\)
\(m_1 = \frac{1}{2}\)
For Line 2:
\(m_2 = \frac{-8 - 2}{2 - (-3)}\)
\(m_2 = \frac{-8 - 2}{2 +3}\)
\(m_2 = \frac{-10}{5}\)
\(m_2 = -2\)
The lines are not parallel because \(m_1 \ne m_2\)
However, they are perpendicular, because:
\(m_1 = -\frac{1}{m_2}\)
To prove this, substitute values for m1 and m2
\(\frac{1}{2} = -\frac{1}{-2}\)
\(\frac{1}{2} = \frac{1}{2}\) --- Proved
Related Questions
Use the map shown below to find the distance between cities A and B to the nearest tenth.

Answers
Answer:
Use the Pythagorean theorem
Step-by-step explanation:

Find the value of n for which the division of x^2n-1 by x+3 leave remainder of -80.
Answers
The value of 'n' for which the division of x^(2n-1) by x + 3 leaves a remainder of -80 is n = 1.
To find the value of 'n' for which the division of x^(2n-1) by x + 3 leaves a remainder of -80, we can use polynomial long division. Let's perform the division step by step:
Write the dividend and divisor in polynomial long division format:
_________________________
x + 3 │ x^(2n-1) + 0x^(2n-2) + 0x^(2n-3) + ...
Divide the leading term of the dividend (x^(2n-1)) by the leading term of the divisor (x). The result is x^(2n-1)/x = x^(2n-2).
Multiply the divisor (x + 3) by the quotient obtained in the previous step (x^(2n-2)). The result is x^(2n-2) * (x + 3) = x^(2n-1) + 3x^(2n-2).
Subtract the result obtained in step 3 from the original dividend:
x^(2n-1) + 0x^(2n-2) + 0x^(2n-3) + ... - (x^(2n-1) + 3x^(2n-2)) = -3x^(2n-2) + 0x^(2n-3) + ...
Bring down the next term of the dividend (which is 0x^(2n-3)) and repeat steps 2-4 until the remainder is constant.
Since we are given that the remainder is -80, we can set the remainder equal to -80 and solve for 'n'.
-3x^(2n-2) + 0x^(2n-3) + ... = -80
Since the remainder is constant (-80), it means that all the terms with x have been canceled out in the division process. Therefore, we can deduce that the highest power of x in the divisor (x + 3) is 0.
This implies that x^(2n-2) = 0, and for any value of 'n', the exponent 2n-2 should be equal to zero. Solving this equation:
2n-2 = 0
2n = 2
n = 1
Therefore, the value of 'n' for which the division of x^(2n-1) by x + 3 leaves a remainder of -80 is n = 1.
for such more question on remainder
https://brainly.com/question/825875
#SPJ8
The amount spent on movie tickets for 8 people is shown on the dot plot.
X
x
58.00
59.00
$10.00
$11.00
$12.00
Select the data set that matches with this dot plot.
{$10.00, $9.00, $11.00, $9.00, $9.00, $11.00, $12.00, $11.00}
{$10.00, $11.00, $12.00, $12.00, 59.00, $10.00, $9.00, 59.00}
{$10.00, $10.00, $12.00, $12.00, $9.00, 59.00, $10.00, $10.00}
(59.00, $12.00, $10.00 $9.00, $9.00, $9.00. S10.00, S11.00}
Type here to search
Answers
Answer:
math way can help
Step-by-step explanation:
For the function f(x)=x+4−−−−−√
, the average rate of change to the nearest hundredth over the interval 2 ≤ x ≤ 6 is
Answers
The average rate of change of the function f(x) = √(x+4) over the interval 2 ≤ x ≤ 6 is approximately 0.29 to the nearest hundredth.
To find the average rate of change of the function f(x) = √(x+4) over the interval 2 ≤ x ≤ 6, we need to calculate the change in the function divided by the change in the input variable over that interval.
The change in the function between x = 2 and x = 6 is:
f(6) - f(2) = √(6+4) - √(2+4) = √10 - √6
The change in the input variable between x = 2 and x = 6 is:
6 - 2 = 4
So, the average rate of change of the function over the interval 2 ≤ x ≤ 6 is:
(√10 - √6) / 4
To approximate the answer to the nearest hundredth, we can use a calculator or perform long division to get:
(√10 - √6) / 4 ≈ 0.29
For such more questions on function
https://brainly.com/question/11624077
#SPJ8
Which set of angles are complementary in this diagram? Please help <3

Answers
9514 1404 393
Answer:
(c) ∠ECF and ∠BCF
Step-by-step explanation:
Complementary angles total 90°. Here, 90° angle BCE is divided by ray CF into two complementary angles. They necessarily have a total of 90°.
∠ECF and ∠BCF
5x-7=11
How to write into word expression
Answers
Answer: Five times a number minus seven equals eleven.
hw to solve 6x-12/3+4=18/x
Answers
The two solutions of the equation:
(6x - 12)/3 + 4 = 18/x
Are x = 3 and x = -3
How to solve the equation?Here we have the following equation:
(6x - 12)/3 + 4 = 18/x
Notice that in the right side we have x on a denominator, then x can not be zero, so x ≠ 0.
Now, let's start by simplifying the left side:
(6x - 12)/3+ 4 = 18/x
2x - 4 + 4 = 18/x
2x = 18/x
Now we can multiply both sides by x so we get:
2x^2 = 18
Now divide both sides by 2:
x^2 = 18/2
x^2 = 9
Finally, apply the square root in both sides:
√x^2 = ±√9
x = ±3
The two solutions are x = 3 and x = -3
Learn more about equations:
https://brainly.com/question/22688504
#SPJ1
Listed below is a table showing the number of employees. 20 years or older by gender in the United states
Answers
The total number of workers that were studied can be found to be 139,340,000.
The percent of workers unemployed would be 5. 4 %.
Percentage of unemployed men is 5. 6 % and unemployed women is 5. 1%.
How to find the employment figures ?Number of employed workers :
= 74,624,000 + 64, 716, 000
= 139,340,000
Percentage unemployed :
= ( 4, 209,000 + 3,314,000 ) / 139,340,000
= 5. 4 %
Percentage of unemployed men :
= 4,209,000 / 74,624,000
= 5.6 %
Percentage of unemployed women:
= 3,314,000 / 64, 716, 000
= 5. 1 %
Find out more on unemployment at https://brainly.com/question/13280244
#SPJ1
The full question is:
a. How many workers were studied?
b. What percent of the workers were unemployed?
c. Compare the percent unemployed for the men and the women.

Simplify the expression StartFraction a b Superscript 3 Baseline over a Superscript 4 Baseline b EndFraction plus left-parenthesis c Superscript 2 Baseline right-parenthesis Superscript 3 Baseline
Answers
The simplification of the expression ab³/a⁴b + (c²)³ is determined as b²/a³ + c⁶.
What is the simplification of the expression?The given expression is simplified as follows;
The given expression is written as;
ab³/a⁴b + (c²)³
To simplify the expression given above, we will divide the fraction with the common factor as follows;
From the numerator; ab³, we will factor out "ab"
From denominator; a⁴b, we will factor out "ab"
The resulting expression becomes;
ab³/a⁴b + (c²)³
= b²/a³ + c⁶
Note: for the power of c, we simplify by multiplying 2 and 3 = 6
Thus, the simplification of the expression ab³/a⁴b + (c²)³ is determined as b²/a³ + c⁶.
Learn more about simplification here: https://brainly.com/question/28008382
#SPJ1
A university's freshman class has 3000 students. 21% of those students are majoring
in Engineering. How many students in the freshman class are Engineering majors?
Answers
Answer: 630
Step-by-step explanation:
\(3000 * 21 /100 = 3000 * 0.21 = 630\)
Giving brainly to the correct answer!
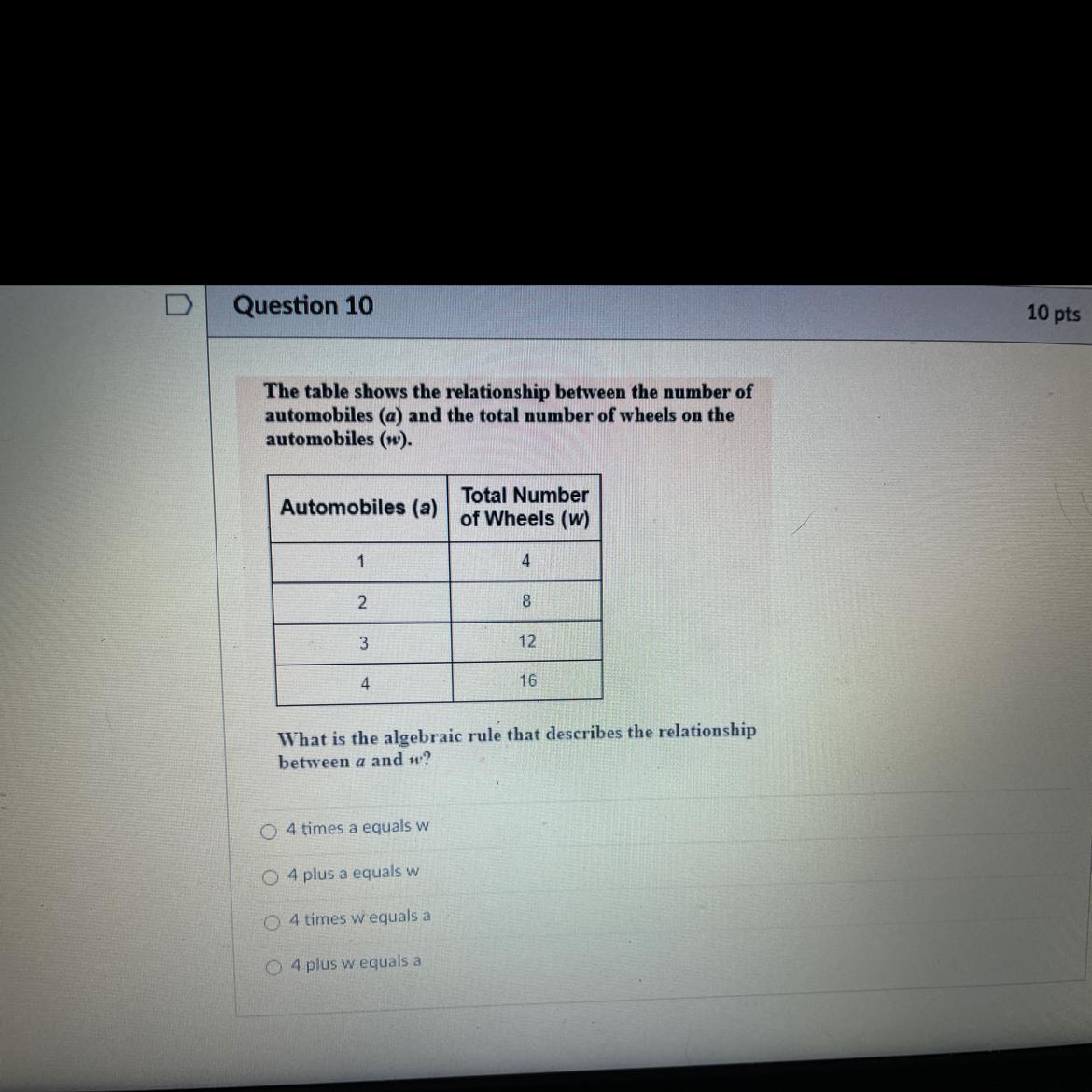
Answers
Answer: A
Step-by-step explanation:
Well four weels in every car so it’s 4 times cars (a)
4 times A=W
Step-by-step explanation: im smart also if u do multiply it by a by 4 it equals W
Two brothers, Charles and David, each inherit $5000. Charles invests his inheritance in a savings account with an annual return of 2.1 %, while David invests his inheritance in a CD paying 5.4 % annually. How much more money than Charles does David have after 1 year?
Answers
Answer: $165
Step-by-step explanation:
It appears that the interest rate is simple interest, that is calculated at the end of each year.
if that is the case, then Mark will receive an interest payment of $5000 x 2.1 = $105
Charles will receive an interest payment of $5000x 0.054 = $270
so, Charles will receive $270 - 105 = $165 more than Mark
at chickfila it cost 7.99 for a chicken sandwich meal , which includes a side of fries and a drink. An extra side costs 1.44. if Ciara wants to purchase a chicken sandwich meal with an additional side of mac &cheese, how much money will she spend?
Answers
Answer: 9.43$ is the answer
regular number after 167, 118, 82, 57, 41, ?
Answers
Answer...
32!!
Step-by-step explanation:
Subtract the numbers to see a pattern of decreasing odd numbers
167-118 = 49
118-82 = 36
82-57 = 25
57-41 = 16
The difference between is 13 then 11 then 9 so the next number should be x-7
The graph shows the solution to a system of inequalities:
pe
Which of the following inequalities is modeled by the graph?
O 2x + 5y = 14; x = 0
O2x + 5y s 14; x 20
O2x - 5y 14; x 20
O-2x - 5y 14; x = 0

Answers
Answer: option (2)
Step-by-step explanation:
The slanted line has a negative slope.
Eliminate options 3 and 4.Also, the line is shaded below.
Eliminate option 1.This leaves option (2) as the correct answer.
The side of a triangle are in the ratio 4:4:3 what kind of triangle is it (b) calculate the smallest angle of the triangle to the nearest degree
Answers
The smallest angle of the equilateral triangle is 60 degrees
If the sides of a triangle are in the ratio 4:4:3, it implies that the lengths of the sides are proportional.
To determine the type of triangle, we examine the side lengths. Since all three sides are equal in length, we have an equilateral triangle.
For an equilateral triangle, all angles are equal. To calculate the smallest angle, we divide the total sum of angles in a triangle (180 degrees) by the number of angles, which is 3:
Smallest angle \(= \frac{180}{3} = 60\)\) degrees.
Therefore, the smallest angle of the equilateral triangle is 60 degrees (to the nearest degree).
For more questions on equilateral triangle:
https://brainly.com/question/17264112
#SPJ8
A survey found that women's heights are normally distributed with mean 63.6 in and standard deviation 2.5 in. A branch of the military requires women's heights to be between 58 in and 80 in.
a. Find the percentage of women meeting the height requirement. Are many women being denied the opportunity to join this branch of the military because they are too short or too tall?
b. If this branch of the military changes the height requirements so that all women are eligible except the shortest 1% and the tallest 2%, what are the new height requirements?
Answers
Answer:
(A)
Step-by-step explanation:
The survey follows of women's height a normal distribution.
The height of 98.51% of women that meet the height requirement are between 58 inches and 80 inches.
The new height requirements would be 57.7 to 68.6 inches
The given parameters are:
\mathbf{\mu = 63.5}μ=63.5 --- mean
\mathbf{\sigma = 2.5}σ=2.5 --- standard deviation
(a) Percentage of women between 58 and 80 inches
This means that: x = 58 and x = 80
When x = 58, the z-score is:
\mathbf{z= \frac{x - \mu}{\sigma}}z=
σ
x−μ
This gives
\mathbf{z_1= \frac{58 - 63.5}{2.5}}z
1
=
2.5
58−63.5
\mathbf{z_1= \frac{-5.5}{2.5}}z
1
=
2.5
−5.5
\mathbf{z_1= -2.2}z
1
=−2.2
When x = 80, the z-score is:
\mathbf{z_2= \frac{80 - 63.5}{2.5}}z
2
=
2.5
80−63.5
\mathbf{z_2= \frac{16.5}{2.5}}z
2
=
2.5
16.5
\mathbf{z_2= 6.6}z
2
=6.6
So, the percentage of women is:
\mathbf{p = P(z < z_2) - P(z < z_1)}p=P(z<z
2
)−P(z<z
1
)
Substitute known values
\mathbf{p = P(z < 6.6) - P(z < -2.2)}p=P(z<6.6)−P(z<−2.2)
Using the p-value table, we have:
\mathbf{p = 0.9999982 - 0.0139034}p=0.9999982−0.0139034
\mathbf{p = 0.9860948}p=0.9860948
Express as percentage
\mathbf{p = 0.9860948 \times 100\%}p=0.9860948×100%
\mathbf{p = 98.60948\%}p=98.60948%
Approximate
\mathbf{p = 98.61\%}p=98.61%
This means that:
The height of 98.51% of women that meet the height requirement are between 58 inches and 80 inches.
So, many women (outside this range) would be denied the opportunity, because they are either too short or too tall.
(b) Change of requirement
Shortest = 1%
Tallest = 2%
If the tallest is 2%, then the upper end of the shortest range is 98% (i.e. 100% - 2%).
So, we have:
Shortest = 1% to 98%
This means that:
The p values are: 1% to 98%
Using the z-score table
When p = 1%, z = -2.32635
When p = 98%, z = 2.05375
Next, we calculate the x values from \mathbf{z= \frac{x - \mu}{\sigma}}z=
σ
x−μ
Substitute \mathbf{z = -2.32635}z=−2.32635
\mathbf{-2.32635 = \frac{x - 63.5}{2.5}}−2.32635=
2.5
x−63.5
Multiply through by 2.5
\mathbf{-2.32635 \times 2.5= x - 63.5}−2.32635×2.5=x−63.5
Make x the subject
\mathbf{x = -2.32635 \times 2.5 + 63.5}x=−2.32635×2.5+63.5
\mathbf{x = 57.684125}x=57.684125
Approximate
\mathbf{x = 57.7}x=57.7
Similarly, substitute \mathbf{z = 2.05375}z=2.05375 in \mathbf{z= \frac{x - \mu}{\sigma}}z=
σ
x−μ
\mathbf{2.05375= \frac{x - 63.5}{2.5}}2.05375=
2.5
x−63.5
Multiply through by 2.5
\mathbf{2.05375\times 2.5= x - 63.5}2.05375×2.5=x−63.5
Make x the subject
\mathbf{x= 2.05375\times 2.5 + 63.5}x=2.05375×2.5+63.5
\mathbf{x= 68.634375}x=68.634375
Approximate
\mathbf{x= 68.6}x=68.6
Hence, the new height requirements would be 57.7 to 68.6 inches
What is one website you can visit in order to request free credit report from any of the three bureaus?
Answers
Answer: annualcreditreport.com
Step-by-step explanation: The only authorized website for free credit reports, or call 1-877-322-8228
A. A tree T with 21 vertices has only vertices of degree 1, 3, 5, and 6. If T has exactly 15 leaves and one vertex of degree 6, how many vertices of T have degree 5? B. A tree T with 35 vertices has 25 leaves, two vertices of degree 2, three vertices of degree 4, one vertex of degree 5, and two vertices of degree 6. It also contains two vertices of the same degree x. What is x? C. A tree with 50 leaves has an equal number of vertices of degree 2, 3, 4, and 5, and no vertices of degree greater than 5. How many vertices are in T?
Answers
A. There are\(\boxed{3}\)vertices of degree 5.
B. the two vertices of the same degree are \(\boxed{2}.\)
A. Let a, b, c, and d be the number of vertices of degree 1, 3, 5, and 6, respectively. We have the following system of equations based on the given information:
\(a + b + c + d &= 21 \ a + 3b + 5c + 6d &= 2 \cdot 21 - 15 = 27 \ d &= 1 \c &= ?\end{align*}\)
The second equation comes from the handshaking lemma, which states that the sum of the degrees of the vertices in a graph is equal to twice the number of edges. Since this is a tree, it has n-1 edges, where n is the number of vertices. We know that there are 15 leaves, which are vertices of degree 1, so the sum of the degrees of the other vertices is 2(21-15)=12. We also know that there is one vertex of degree 6, so d=1.
Solving for c, we get c=3. Therefore, there are\(\boxed{3}\)vertices of degree 5.
B. Let a, b, c, d, e, f, and g be the number of vertices of degree 2, 4, 5, 6, x, and leaves, respectively. We have the following system of equations based on the given information:
\(a + b + c + d + e + f + g\)
&= \(35 \ 2a + 4b + 5c + 6d + xe + g &= 2 \cdot 35 - 2 - 3 \cdot 4 - 5 - 6 \cdot 2 = 10 + xe \x &\geq 2 \x &= ?\end{align*}\)
The second equation comes from the handshaking lemma, and we use the given information to find the total sum of degrees. We also know that \(x\geq 2\), since the graph contains at least two vertices of degree x.
Since \(g=25\), we have a =\(35 - 25 - b - c - d - e - f = 10 - b - c - d - e - f.\)Substituting this into the second equation, we get \(2(10-b-c-d-e-f)+4b+5c+6d+xe+25=10+xe\), which simplifies to \(b+3c+4d+xe=7-2e.\)
Since b, c, d, e, and f are all non-negative integers, we see that x=2 is the only possibility. This is because if \(x\geq 3\), then the left side of the equation \(b+3c+4d+xe=7-2e\) would be at least 7, but the right side is at most 5, a contradiction. Therefore, the two vertices of the same degree are \(\boxed{2}.\)
C. Let a, b, c, and d be the number of vertices of degree 2, 3, 4, and 5, respectively. We have the following system of equations based on the given information:
\(a + b + c + d &= 50 \ a + 2b + 3c + 4d + 5d &= 2 \cdot 50 - 1 = 99 \\end\)
for such more question on vertices
https://brainly.com/question/28747454
#SPJ4
find the slope of the line that passes through the points (20,8) and (9,16)
Answers
Answer:
slope: \(-\frac{8}{11}\)
slope-intercept form: y= \(-\frac{8}{11}\)x+\(\frac{248}{11}\)
Step-by-step explanation:
Hope this helps!
Please help me with this

Answers
Answer:
7^-3+5 (5 goes up and becomes+5)
so ans is 7^2
Answer:
7^2\( \frac{ {7}^{ - 3} }{ {7}^{ - 5} } = {7}^{ - 3 + 5} = {7}^{2} \)
You choose a marble at random from a bag contains 12 red 10 blue 5 green 4 yellow and 29 black marbles. The marble is red.

Answers
Step-by-step explanation:
P(red) = 12/(12+10+5+4+29)
= 12/60
= 1/5
= 0.2
= 20%
show the lowest expression 2/3÷5/6
Answers
Answer:
4/5
Step-by-step explanation:
Answer:
4/5 is the lowest expression for 2/3÷5\6
The answer is 3(sign)2 I need help with the work

Answers
First, notice that the two sides of the right triangle are equal, then, using the pythagorean theorem,we get:
\(\begin{gathered} 6=\sqrt[]{x^2+x^2}=\sqrt[]{2x^2} \\ \Rightarrow\sqrt[]{2}x=6 \\ \Rightarrow x=\frac{6}{\sqrt[]{2}}\cdot(\frac{\sqrt[]{2}}{\sqrt[]{2}})=\frac{6\sqrt[]{2}}{2}=3\sqrt[]{2}_{} \\ x=3\sqrt[]{2} \end{gathered}\)therefore, x = 3*sqrt(2)
A
-2+
Which graph represents the
function y = tan x?
B
2T
2T
D
-2+1
21
4+
ㅠ
2T
2πT

Answers
The graph that represents the function y= tanx is Option A.
What is the description of the above function?The graph of y =tan (x) is a periodic function that has vertical asymptotes at x = (n + 1/2)π, where n is an integer.
It oscillates between positive and negative infinity, creating a wave- like pattern.
It has a repeating pattern of sharp peaks and valleys, exhibiting both positive and negative slopes.
Thus, option A is the correct answer.
Learn more about graph:
https://brainly.com/question/25184007
#SPJ1

For the polynomial below, -3 and -1 are zeros.
g(x)=x² +6x³
+9x²-2x-6
Express g (x) as a product of linear factors.
Answers
The complete factorization of the polynomial is:
h(x) = (x - 3)*(x - 1)*(x + 2)
Here we have the polynomial:
g(x)= x³ - 2x² - 5x + 6
And we know that x = 3 is a zero, then (x - 3) is a factor.
So if f(x) = a*x² + b*x + c
We can write:
h(x) = (x - 3)*f(x)
Let's find f(x).
Expanding that:
x³ - 2x² - 5x + 6 = (x - 3)*(a*x² + b*x + c)
x³ - 2x² - 5x + 6 = ax³ + bx² + cx - 3ax² - 3bx - 3c
x³ - 2x² - 5x + 6 = ax³ + (b - 3a)x² + (c - 3b)x - 3c
Comparing like terms, we can see that:
a = 1
b - 3 a = -2
c - 3b = -5
-3c = 6
With the first and last equation we can get:
a = 1
c = 6/-3 = -2
Now with one of these values and the second or third equation we can find the value of b.
b - 3 a = -2
b - 3*1 = -2
b - 3 = -2
b = -2 + 3 = 1
Then:
f(x) = x² + x - 2
The zeros of this quadratic function are given by:
x = -1±3 / 2
so, we get,
x = (-1 + 3)/2 = 1
x = (-1 - 3)/2 = -2
Then we can factorize this as:
f(x) = (x - 1)*(x + 2)
And then we can write h(x) as:
h(x) = (x - 3)*(x - 1)*(x + 2)
Learn more about polynomials at:
brainly.com/question/4142886
#SPJ1
complete question:
For the polynomial below, 3 is a zero.
g(x)= x³ - 2x² - 5x + 6
Express g (x) as a product of linear factors.
Latoya is building a fence around her garden. For every 3 feet of fencing, the cost is $21.
Complete the table below showing the length of the fence and the cost.
Length of fencing (feet)

Answers
PLEASE ANSWER UNDER 5 MIN!!!! ily!!!!
what is the period of the sinusoidal function? enter your answer in the box.

Answers
Answer:
Step-by-step explanation:
10
Ws
Amanda buys a book for 24.97, a backpack for 17.23. and a set of markers for 7.55. she gives the cashier 50.00 how much change does amanda get
Answers
Answer:
She would get 0.25 cents
Step-by-step explanation:
what you would do is add 24.97, 17.23 and 7.55 together and get a total of 49.75 and subtract that from 50 and get 0.25
please mark me brainliest
Answer:0.25
Step-by-step explanation:
Which expression is equivalent to -6(-2/3+2x)
Answers
Answer:
4−12x
Step-by-step explanation: