Teresa is loading her car with boxes that each weigh 4 3/4 pounds. If Teresa loads 9 of theses boxes find the combined weight of each box
Answers
Total weight:-
9(19/4)171/442-3/4lbsRelated Questions
The time, T (seconds) it takes for a pot of water to boil is inversely proportional to the cooker setting, H, applied to the pot.
When H = 4, T = 700.
Work out T when H = 14
Answers
Answer:
200
Step-by-step explanation:
T = x * (1/H)
x = T*H
x = 2800
so for H = 14
T = 2800 * (1/14) = 200
A straight highway is 100 miles long, and each mile is marked by a milepost numbered from 0 to 100. A rest area is going to be built along the highway exactly 7 miles away from milepost 58. If m is the milepost number of the rest area, which of the following equations represents the possible locations for the rest area?
Answers
Answer:
Step-by-step explanation:
The milepost number of the rest area is 7 miles away from milepost 58, so it can be represented by the equation:
m = 58 + 7
This equation states that the milepost number of the rest area is equal to 58 plus 7, or 65. Therefore, the rest area can be located at milepost 65.
Hi I’m lost on this problem and I really need help

Answers
We were given:
\(\begin{gathered} \frac{3x-5}{2}=-7 \\ \text{Cross multiply, we have:} \\ 3x-5=-7\times2 \\ 3x-5=-14 \\ \text{Add ''5'' to both sides, we have:} \\ 3x-5+5=-14+5 \\ 3x=-9 \\ \text{Divide both sides by 3, we have:} \\ x=-3 \end{gathered}\)Therefore, we have the reasons as follows:
1. a. Given
2. b. Multiply both sides by ''2'' to eliminate the fraction
3. c. Put like terms together (by adding ''5'' to both sides)
4. d. Divide both sides by the coefficient of x (divide both sides by ''3'')
Finde the value of x in the proportion ( 5x+ 1 ):3 =(2x +2): 7(6 x) = (4x) :7
Answers
In the proportion (5x + 1):3 = (2x + 2):7, the value of x is -1/29.
In the proportion (6x):(4x) = 7, there is no value of x that satisfies the proportion.
To find the value of x in the given proportions, let's solve them one by one:
(5x + 1) : 3 = (2x + 2) : 7
To solve this proportion, we can cross-multiply:
7(5x + 1) = 3(2x + 2)
35x + 7 = 6x + 6
Subtracting 6x from both sides and subtracting 7 from both sides:
35x - 6x = 6 - 7
29x = -1
Dividing both sides by 29:
x = -1/29
Therefore, the value of x in the first proportion is -1/29.
(6x) : (4x) = 7
To solve this proportion, we can simplify the left side:
6x / 4x = 7
Dividing both sides by 2x:
3/2 = 7
This equation is not true, as 3/2 is not equal to 7.
Therefore, there is no value of x that satisfies the second proportion.
In summary, the value of x in the proportion (5x + 1) : 3 = (2x + 2) : 7 is -1/29, and there is no value of x that satisfies the proportion (6x) : (4x) = 7.
For similar question on proportion.
https://brainly.com/question/29864115
#SPJ8
WS SAMPLE
Find the area of each sector. Round your answers to the nearest tenth.
13)
60° 10 in
Answers
Area of sector would be,
⇒ Area of sector = 102.6 feet squared
We have to given that,
Radius of circle = 14 ft
Angle θ = 60°
Now, We know that,
Area of sector = [θ/360]πr²
Where, r is radius of circle.
Hence, We can substitute all the values, we get;
Area of sector = [θ/360]πr²
Area of sector = [60/360](22/7)(14)²
Area of sector = [1/6][22/7][196]
Area of sector = 102.6 feet squared
Thus, Area of sector would be,
⇒ Area of sector = 102.6 feet squared
Learn more about the circle visit:
https://brainly.com/question/24810873
#SPJ1

Help don’t understand

Answers
Answer:
f(-14) = -6
f(-4) = 6
f(12) = 6
f(0) = -3
negative
Step-by-step explanation:
f(-14) = -6
This is because when x is -14, y is -6, as seen in the graph
f(-4) = 6
This is because when x is -4, y is 6, as seen in the graph
f(12) = 6
This is because when x is 12, y is 6, as seen in the graph
f(0) = -3
This is because when x is 0, y is -3, as seen in the graph
is f(4) positive or negative?
negative
This is because when x is 4, y is -6, as seen in the graph
show that a) cos3∅=cos²∅-3cos∅sin²∅
Answers
The correct proof of the equation is cos3θ =cos(2θ + θ) = cos²θ - 3cosθsin²θ (Proved)
Solving trigonometry identity
Given the trigonometry identity below:
cos3∅=cos²∅-3cos∅sin²∅
We are to prove that both sides of the equation are equal.
cos 3θ = cos(2θ + θ)
Using the double angle formula for cosine, we can expand the first term:
cos(2θ + θ) = cos2θ cos θ - sin2θ sinθ
Since cos2θ = cos²θ - sin²θ
cos(2θ + θ) = cos²θ - sin²θ - 2cosθsinθsinθ
cos(2θ + θ) = cos²θ - sin²θ - 2cosθsin²θ
On simplifying, we can see that;
cos3θ =cos(2θ + θ) = cos²θ - 3cosθsin²θ (Proved)
Learn more on trigonometry here: https://brainly.com/question/7331447
#SPJ1
If x = 2 and y = 3, then 4x
Answers
Answer: 8
Step-by-step explanation: Substituting x for 2 since we know the value, 4(2) is 8.
Answer: 8
Step-by-step explanation:4*2=8
Does anyone know this answer??

Answers
Approximately 99.7% of scores lie in the shaded region.
We have,
The empirical rule, also known as the 68-95-99.7 rule, provides an estimate of the percentage of scores that lie within a certain number of standard deviations from the mean in a normal distribution.
According to this rule:
Approximately 68% of scores lie within 1 standard deviation of the mean.
Approximately 95% of scores lie within 2 standard deviations of the mean.
Approximately 99.7% of scores lie within 3 standard deviations of the mean.
Now,
In the given scenario, the shaded region represents the area between -2 and 3 standard deviations from the mean on the x-axis.
This encompasses the area within 3 standard deviations of the mean.
And,
Since 99.7% of scores lie within 3 standard deviations of the mean, we can estimate that approximately 99.7% of scores lie in the shaded region.
Therefore,
Approximately 99.7% of scores lie in the shaded region.
Learn more about normal distribution here:
https://brainly.com/question/31327019
#SPJ1
FOUR CARS CRASH AT 5 MILES AN HOUR. Cost of the repairs are 422, 456, 401, and 215
COMPUTE RANGE
SAMPLE VARIANCE,
AND SAMPLE STANDARD DEVIATION
Answers
The range of the repairs to the cars is 241.
The sample variance is 11, 671.33
The sample standard deviation would be 108.03.
How to find the range ?Range = Maximum repair cost - Minimum repair cost
= 456 - 215
= 241
How to find the sample variance and standard deviation ?Find mean :
= (422 + 456 + 401 + 215) / 4
= 373. 5
Sample variance :
= Sum of ( each repair cost - mean ) ² / (Number of cars - 1)
= ( 2, 340.25 + 6, 812.25 + 756.25 + 25, 105.25 ) / ( 4 - 1 )
= 11, 671. 33
Sample standard deviation:
= √sample variance
= √11, 671. 33
= 108. 03
Find out more on sample variance at https://brainly.com/question/28542390
#SPJ1
1-
-5-4-3-2-11₁
H
5
4
3
2
Mark this and return
-2+
-3+
AWN
-4
-5
]
[
C
1 2 3 4 5 x
]
What is the range of the function on the graph?
all the real numbers
O all the real numbers greater than or equal to 0
all the real numbers greater than or equal to 2
all the real numbers greater than or equal to -3
Answers
The range of the function on the graph is C. all the real numbers greater than or equal to –3 .
How to get the range?We can see by the graph maximum value of y of function is -3 and the graph continues to extend upward .
So, the range contain all the real numbers greater than or equal to –3 .
Therefore, the range contain all the real numbers greater than or equal to –3 .
Learn more about graph on:
https://brainly.com/question/2043285
#SPJ1
![1--5-4-3-2-11H5432Mark this and return-2+-3+AWN-4-5][C1 2 3 4 5 x]What is the range of the function on](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/Pvvk0ur2vkcYvR9Cj1BaBGmjR2vIazHt.jpeg)
What is the area of a rectangle with a length of Four and two-fourths meters and a width of Seven and five-sixths meters?
Answers
Answer:
the area of the rectangle is 35.25 square meters.
Step-by-step explanation:
To find the area of a rectangle, we multiply the length by the width.
First, we need to convert the mixed numbers to improper fractions to make the multiplication easier:
4 and 2/4 = 4 + 2/4 = 16/4 + 2/4 = 18/4
7 and 5/6 = 7 + 5/6 = 42/6 + 5/6 = 47/6
Now we can multiply the length and width:
Area = (18/4) * (47/6)
Area = (9/2) * (47/6) (canceling the common factor of 2 between 18/4 and 6 in 47/6)
Area = (9 * 47) / (2 * 6)
Area = 423/12
Area = 35.25
Therefore, the area of the rectangle is 35.25 square meters.
Complete the equation describing how
x andy are related
- 0 1 2 3 4 5
y 23 8 13 18 23 28
y = [ ? ]x + [ ]
Enter the answer that belongs in [?].
Enter
![Complete the equation describing howx andy are related- 0 1 2 3 4 5y 23 8 13 18 23 28y = [ ? ]x + [ ]Enter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/6OmIy61Li33lUlFffHKuZiY0miR39nBj.png)
Answers
Answer:
y = 5x + 3Step-by-step explanation:
According to table:
The y - intercept is b = 3 (point (0, 3))The slope is m = 13 - 8 = 5 (points (1, 8) and (2, 13))The equation is:
y = mx + by = 5x + 3The cross-section of this prism is a square with side length 4 m. What is the surface area of the prism?
(photo attached below.)

Answers
The final answer for the surface area of the prism is 32 m^2 + 16h m^2.
To find the surface area of the prism, we need to calculate the area of each face and sum them up.
The prism has two identical square faces and four rectangular faces. The square face has a side length of 4 m. The area of one square face is given by:
Area of square face = side length^2 = 4^2 = 16 m^2
Since there are two square faces, the total area of the square faces is:
Total area of square faces = \(2 * 16 = 32 m^2\)
The rectangular faces have a length equal to the side length of the square face (4 m) and a width equal to the height of the prism. Let's assume the height of the prism is h. The area of one rectangular face is given by:
Area of rectangular face = length * width = \(4 * h = 4h m^2\)
Since there are four rectangular faces, the total area of the rectangular faces is:
Total area of rectangular faces = \(4 * 4h = 16h m^2\)
Therefore, the surface area of the prism is the sum of the areas of the square and rectangular faces:
Surface area of prism = Total area of square faces + Total area of rectangular faces
= \(32 m^2 + 16h m^2\)
= \(32 m^2 + 16h m^2\)
The answer for the surface area of the prism is 32 m^2 + 16h m^2.
For more questions on prism
https://brainly.com/question/23963432
#SPJ8
Dale runs 3 miles in 28 minutes. At the same rate, how many miles would he run in 42 minutes?

Answers
Answer:
He would run 4.5 miles in 42 minutes if the rate is the same!
Step-by-step explanation:
solve for x in the simplest form

Answers
Answer:
x= 12/5
Step-by-step explanation:
Distribute the fraction and solve for x.

Compute the sum of all nine 2-digit numbers with a ones digit of 6.
Answers
Answer: 504
Step-by-step explanation:
Answer:504
Step-by-step explanation:
which image is the translation of triangle ABC given by the translation rule (x,y) (x-2,y+3)
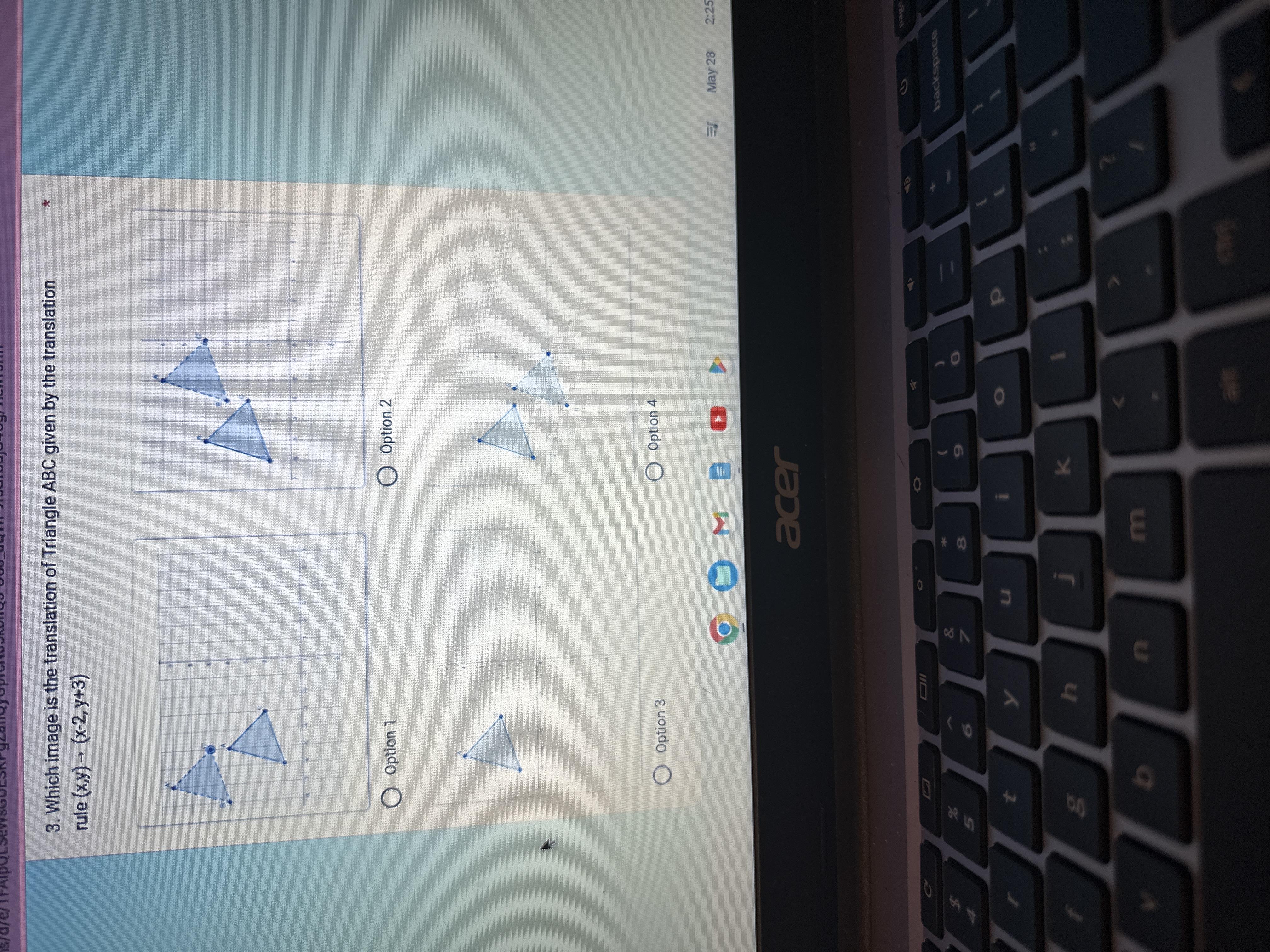
Answers
The coordinates of the image of triangle ABC would be A (-1, -1), B (3, 2), and C (4, -6) after translation, and if the original coordinates are A(-3,2) B(1,5) C(2,-3).
We know that,
A point is transformed when it is moved from where it was originally to a new location. Translation, rotation, reflection, and dilation are examples of different transformations.
Let assume A(-3,2) B(1,5) and C (2,-3) are original coordinates
The following translation is being used: (x, y) ⇒ (x + 2, y - 3)
First, take your x-coordinates and add them by two because it is the translation utilized to solve for your x-coordinate.
You would receive the following for yours x's: A (-1, y ) B (3, y) C (4, y)
Next, remove three from each of your y-coordinates because it is the translation being utilized to solve for your y-coordinate.
You would receive the following for your y's: A (x, -1) B (x, 2) C (x, -6)
Finally, you would take each one and put it together, or piece it together.
Hence, the coordinates of the image of triangle ABC after translation would be A (-1, -1), B (3, 2), and C (4, -6).
To learn more about the transformations click here :
brainly.com/question/28029674
#SPJ1
find the first 4 terms and the 10th term from 3n+4
Answers
Answer:
16 and 34
Step-by-step explanation:
The general form = 3n+4
The 4th term = 3(4)+4 = 12+4 = 16
The 10th term = 3(10)+4= 30+4= 34
Assume a random variable representing the amount of time it takes for a customer service representative to pick up has a uniform distribution between 15 and 20 minutes. What is the probability that a randomly selected application from this distribution took less than 18 minutes
Answers
Answer:
0.6 = 60% probability that a randomly selected application from this distribution took less than 18 minutes.
Step-by-step explanation:
Uniform probability distribution:
An uniform distribution has two bounds, a and b.
The probability of finding a value of at lower than x is:
\(P(X < x) = \frac{x - a}{b - a}\)
The probability of finding a value between c and d is:
\(P(c \leq X \leq d) = \frac{d - c}{b - a}\)
The probability of finding a value above x is:
\(P(X > x) = \frac{b - x}{b - a}\)
Uniform distribution between 15 and 20 minutes.
This means that \(a = 15, b = 20\)
What is the probability that a randomly selected application from this distribution took less than 18 minutes?
\(P(X < 18) = \frac{18 - 15}{20 - 15} = 0.6\)
0.6 = 60% probability that a randomly selected application from this distribution took less than 18 minutes.
Graph
y - 6 = 4 ( x - 4 )
Answers
Step-by-step explanation:
First, we need to get it to slope-intercept form:
So you distribute the 4 to x-4:
4x-16
now the equation looks like this:
y-6=4x-16
now move the -6 to the other side:
y=4x-10
Answer:
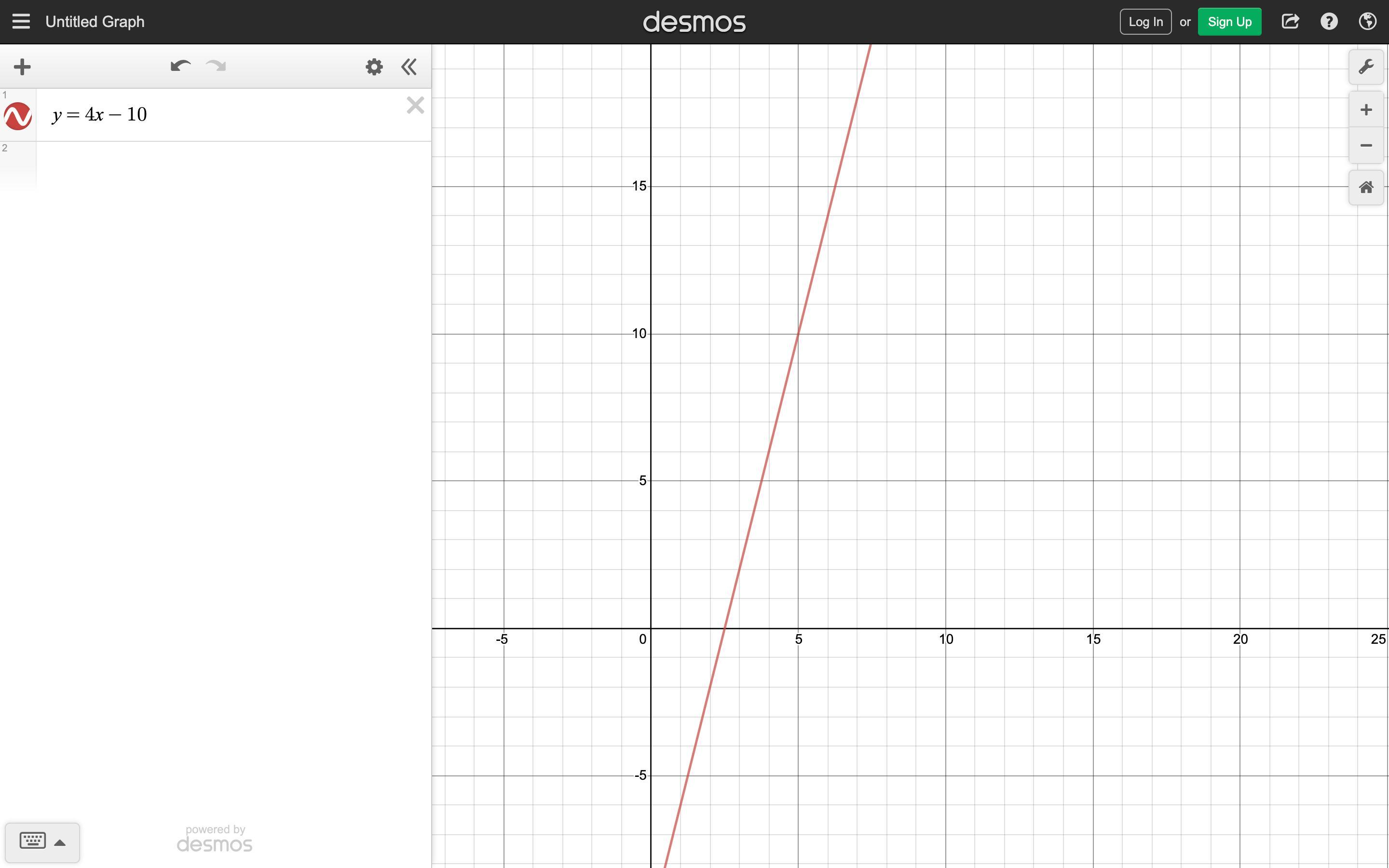
The graph of the equation y - 6 = 4(x - 4) is attached at the end.
To graph the equation y - 6 = 4(x - 4), rewrite it in slope-intercept form by solving for y:
y - 6 = 4(x - 4)
y - 6 = 4x - 16
y = 4x - 16 + 6
y = 4x - 10
Now, the slope (m) is 4 and the y-intercept (b) is -10.
To graph the equation, plot a few points and draw a straight line passing through those points.
Choose some x-values and calculate the corresponding y-values:
For x = 0, y = 4(0) - 10 = -10
For x = 2, y = 4(2) - 10 = -2
For x = 4, y = 4(4) - 10 = 6
For x = 6, y = 4(6) - 10 = 14
Learn more about Graph here:
https://brainly.com/question/28872677
#SPJ4

Determine whether the graph represents a function.

Answers
A, the relation is not a function
in order for something to be a function, x (the input) can't repeat itself more than once
3 coins are flipped.

Answers
Answer:
just keep writing down outcome on a sheet of paper then count total
Step-by-step explanation:
assuming an interest rate of 5.4 percent, what is the value of the following cash flows four years from today? year cash flow 1 $ 3,000 2 4,040 3 5,885 4 7,975 multiple choice $23,120.48 $21,291.46 $22,178.61 $22,609.26 $23,631.70
Answers
The value of the cash flows four years from today is $22,609.26.
The value of a set of cash flows can be calculated using the present value of an annuity formula. This formula takes into account the time value of money, which states that money has a different value at different points in time due to the opportunity cost of the money. In other words, the money you have today is more valuable than the money you will have in the future.
The present value of an annuity formula is PV = CF / (1 + r)^n, where PV is the present value, CF is the cash flow, r is the interest rate, and n is the number of periods. In this example, the cash flows are $3,000, $4,040, $5,885, and $7,975, the interest rate is 5.4%, and the number of periods is 4. Plugging these numbers into the formula, the present value is $22,609.26. This is the value of the cash flows four years from today.
The value of the cash flows four years from today is $22,609.26.
Learn more about annuity here:
https://brainly.com/question/29297706
#SPJ4
What is the equation in point-slope form of the line that passes through the point (−1,−4) and has a slope of –3? Drag and drop the appropriate number, symbol, or variable to each box.
Answers
Answer:
y+4=-3(x+1)
Step-by-step explanation:
Hope this helps may all your sweet dreams come true!
Answer:
y+4=-3(x+1)
Step-by-step explanation:
this is right im in the test
If a cube has volume 125cm³, find the height of the cube.
Answers
Answer:
height = 5 cm
Step-by-step explanation:
a cube has congruent sides (s)
the volume (V) of a cube is calculated as
V = s³
given V = 125 , then
s³ = 125 ( take cube root of both sides )
\(\sqrt[3]{s^3}\) = \(\sqrt[3]{125}\) = \(\sqrt[3]{5^3}\)
s = 5
then height = 5 cm
There are five questions listed below. Each question includes the quantity 37. Match the 37 in each question on the left to which part of
the problem it represents on the right -- the base, percent, or amount. Some answer options on the right will be used more than once.
12 is 37 % of what number?
percent
What is 52% of 37?
37 is what percent of 254?
What percent of 37 is 5?
What number is 20 % of 37?
base
amount
Answers
The solution of different problem in Percentage and number is 32.43,19.24,14.566%,13.51%,7.4
What is the percentage?A percentage is a numerical representation of a portion or proportion of a whole, expressed as a fraction of 100. It is commonly denoted by the symbol "%" (percent), which literally means "per hundred." It is often used to quantify and compare relative values, rates, or quantities in various contexts.
According to the given information:
12 is 37 % of what number?
12=37% OF X
12=37/100*X
X=12*100/37
x=32.43
What is 52% of 37?
52*37/100
19.24
37 is what percent of 254?
37=X%OF254
37=X*254/100
X=37*100/254
14.566%
What percent of 37 is 5?
X%OF37=5
X*37/100=5
X=500/37
13.51%
What number is 20 % of 37?
20*37/100
7.4
To know more about Number Visit: https://brainly.com/question/17429689
#SPJ1
Describe the secant and cosecant functions.
please help
Answers
The functions secant (sec θ = hypotenuse/adjacent side = 1/cos θ) and cosecant (cosec θ = hypotenuse/opposite side = 1/sin θ).
secant function:
The secant function is a periodic function in trigonometry.The secant function or sec function can be defined as the ratio of the length of the hypotenuse to that of the length of the adjacent side of an right angled triangle.
That is,
sec θ = hypotenuse/adjacent side
It is also known as reciprocal of cosine function.
sec θ = 1/cos θ
cosecant function:
The cosecant function is the reciprocal of the sine function.The cosecant function or cosec function can be defined as the ratio of the length of the hypotenuse to that of the length of the opposite side of an right angled triangle.
That is,
cosec θ = hypotenuse/opposite side
cosec θ = 1/sin θ
Therefore the functions secant (sec θ = hypotenuse/adjacent side = 1/cos θ) and cosecant (cosec θ = hypotenuse/opposite side = 1/sin θ).
Learn more about secant and cosecant here:
https://brainly.com/question/2272598
#SPJ1
At age 25, Sam deposited $4,000 into an IRA account where it earns 9.8% interest, compounded monthly. What will it be worth when Sam is 33?
Answers
The amount $4,000 deposited by Sam into an IRA account where it earns 9.8% interest, compounded monthly, will be $12903.8 when Sam is 33.
What is compound interest?Compound interest is the amount charged on the principal amount and the accumulated interest with a fixed rate of interest for a time period.
The formula for the final amount with the compound interest formula can be given as,
\(A=P\times\left(1+\dfrac{r}{n\times100}\right)^{nt}\\\)
Here, A is the final amount (principal plus interest amount) on the principal amount P of with the rate r of in the time period of t.
At age 25, Sam deposited $4,000 into an IRA account where it earns 9.8% interest, compounded monthly. Thus,
\(P=4000\\r=9.8\%\)
Now the worth has to be found out when Sam is 33. Thus, the total time period in year is,
\(t=33-25\\t=12\rm\; years\)
Put the values in the formula,
\(A=4000\times\left(1+\dfrac{9.8}{12\times100}\right)^{12\times12}\\A\approx12903.8\)
Thus, the amount $4,000 deposited by Sam into an IRA account where it earns 9.8% interest, compounded monthly, will be $12903.8 when Sam is 33.
Learn more about the compound interest here;
https://brainly.com/question/24274034
#SPJ1
Answer: $8733.01
Step-by-step explanation: I got it right on my quiz
(-8x^4y^2)^2*2x^2y^6 divided by32x^8y^3
Answers
Answer:
The answer is 4x^2y^4y^3 simplified to 4x^2y^7
Step-by-step explanation: