The Area of a rectangular carpet is 18 m2. The length of the carpet is 3m longer than the width. How long is the carpet
Answers
The Area of a rectangular carpet is 18 m2. The length of the carpet is 3m longer than the width. How long is the carpet
we have that
the area of a rectangle is equal to
A=L*W
In this problem we have
A=18 m2
L=W+3
substitute the given values
18=(W+3)*W
solve for W
18=w^2+3w
w^2+3w-18=0
solve the quadratic equation by graphing
see the attached figure
the solutions are
w=-6 and w=3
Find the value of L
L=W+3
L=3+3
L=6

Related Questions
Roberta sold goods costing $35,500, her expenses totaled $2,500 and her freight in totaled $750.
Her company's average stock of goods during the same period was $9,500.
The inventory turnover ratio for Roberta's company is
Answers
Answer:
Inventory turnover ratio is 3.74
explanation:
Inventory turnover is a ratio of the number of times a company's inventory is sold and replaced in a given period.
Inventory turn over ratio is calculated as ; Cost of goods sold ÷ Average stock of goods sold
= $35,500 / $9500
= 3.74
A farmer earns $___ for each orange she sells. She had to pay $___ for fertilizer. Part A: Rewrite the description by filling in the blanks with values of your choice to show the amount of money the farmer could earn selling any number of oranges, n. Make sure the values you choose make sense for this situation. (6 points) Part B: Write an algebraic expression from your written description used in Part A. Let n stand for the number of oranges. (6 points)
Answers
Part B: The algebraic expression for the amount of money the farmer could earn selling any number of oranges, n, is 0.20n - 25.
Find the complete factored form of the
polynomial :
-8m²n-7m² nª
Enter the correct answer.
Answers
The polynomial -8m²n - 7m²n can be factored using the common factor -m²n. The complete factored form of the polynomial is (-m²n) (8 + 7a).
To find the complete factored form of the polynomial -8m²n - 7m²n, we can factor out common terms from both the terms. The common factor in the terms -8m²n and -7m²n is -m²n. We can write the polynomial as:
-8m²n - 7m²n = (-m²n) (8 + 7a)
Therefore, the complete factored form of the polynomial -8m²n - 7m²n is (-m²n) (8 + 7a). This expression represents the original polynomial in a multiplied form. We can expand this expression using distributive law to verify that it is equivalent to the original polynomial.
For more such questions on polynomial, click on:
https://brainly.com/question/1600696
#SPJ8
Write a system of linear equations given each table. Then name the solution.

Answers
Answer:
Choose
a
,
b
and
c
the make the equation true.
Step-by-step explanation:
A linear equation can be written in several forms. "Standard Form" is
a
x
+
b
y
=
c
where
a
,
b
and
c
are constants (numbers).
We want to make two equations that
(i) have this form,
(ii) do not have all the same solutions (the equations are not equivalent), and
(iii)
(
4
,
−
3
)
is a solution to both.
a
x
+
b
y
=
c
. We want
a
,
b
and
c
so that
a
(
4
)
+
b
(
−
3
)
=
c
How to solve
(2.31*10^-6)+(3.41*10^3)
Answers
2.31 x 10^-6+3.41 x 10^3
Convert the decimal to a fraction
231/100 x 10^-6 + 3.41 x 10^3
Multiply
231/100 x 1/10^6 + 3.41 x 1000
Combine
231/100 x 1/10^6 + 3410
Calculate
231/(10^2 x 10^6) + 3410
Answer:
231/10^8 + 3410
Hope it helped :)
Aircraft A has 105 more seats than aircraft B. If their total number of seats is 701, find the number of seats for each aircraft.
Aircraft A has how many seats?
Answers
Answer:
Aircraft A: 403 seats
Aircraft B: 298 seats
Step-by-step explanation:
Let's x represent the seats in Aircraft B
We have the equations:
Aircraft A: (x + 105)
Aircraft B: x
We Know
Their total number of seats is 701; find the number of seats for each aircraft.
We Take
x + (x + 105) = 701
2x + 105 = 701
2x = 596
x = 298 seats
So, there are 298 seats in Aircraft B
Aircraft A has how many seats?
We Take
701 - 298 = 403 seats
So, there are 403 seats in Aircraft A
Final Answers:
Aircraft A: 403 seats
Aircraft B: 298 seats
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
Drag each tile to the correct box. Not all tiles will be used. Arrange the steps to solve the equation x + 3 − 2 x − 1 = - 2 . Simplify to obtain the final radical term on one side of the equation. Raise both sides of the equation to the power of 2. Apply the Zero Product Rule. Use the quadratic formula to find the values of x. Simplify to get a quadratic equation. Raise both sides of the equation to the power of 2 again.

Answers
The value of x = 16 + 4\(\sqrt{15}\)
Given,
To solve the equations :
\(\sqrt{x+3} - \sqrt{x -1}\) = -2
Solve by the given steps :
Now, According to the question:
Step 1: Simplify to obtain the radical form on one side of the equation:
\(\sqrt{x+3} - \sqrt{x -1}\) = -2
Step 2: Raise both sides of the equation to the power of 2
\((\sqrt{x+3} - \sqrt{x -1})^2 = (-2)^2\)
x + 3 + 2x - 1 -2 \(\sqrt{(x+3)(2x -1)}\) = 4
3x - 2 = 2 \(\sqrt{(x+3)(2x -1)}\)
\((3x - 2)^2 = [2\sqrt{(x+3)(2x -1)}]^2\)
9\(x^{2}\) - 12x + 4 = 4 (2\(x^{2}\) + 5x -3)
Step 3: Apply the zero product rule, Simplify to get a quadratic equation :
\(x^{2}\) - 32x +16 = 0
Step 4: Use the quadratic formula to find the values of x :
\(x^{2}\) - 32x + 16 =0
x = 16 + 4\(\sqrt{15}\) and x = 16 - 4\(\sqrt{15}\)
x = 16 - 4\(\sqrt{15}\) (It is rejected)
So, the value of x = 16 + 4\(\sqrt{15}\)
Learn more about Quadratic Formula at:
https://brainly.com/question/9300679
#SPJ1
Answer: Raise both sides of the equation to the power of 2
simplify to obtain the final radical term on one side of the equation
raise both sides of the equation to the power of 2 again
simplify to get a quadratic equation
use the quadratic formula to find the xvalues
Step-by-step explanation:
Use Substitution to solve each system of equations.

Answers
Answer:
x = -3
y = -2
(-3, -2)
Step-by-step explanation:
x - 7y = 11
5x + 4y = -23
-----------------------
-5 (x - 7y = 11)
-5x + 35y = -55
--------------------------
-5x + 35y = -55
5x + 4y = -23
39y = -78
÷39 ÷39
y = -2
-----------------------------
x - 7y = 11
x -7(-2) = 11
x + 14 = 11
-14 -14
x = -3
I hope this helps!
What is the value of angle PDV

Answers
Answer:
9y+7=2y+98
7y+7=98
7y = 91
y = 13
m<PDV = 2y+98
= 2(13)+98
= 26+98
= 124
Please find the square root. Round your answer to the nearest tenth.
√81.4 =
Answers
0Answer: 9.0
Step-by-step explanation:
.
What is the sum of: 1 + x + x2 + x3 + x4 + x5 + ⋯ + x100?
Answers
The Sum is 1+ x² + x³ + \(x^4\) + \(x^5\) + ⋯ + \(x^{100\) = \(\sum^{100} _ {n=0}\) 1/( 1- x)
What is Series?A finite series is one that has a finite number of terms.
If the series \(a_1\)+ \(a_2\) + \(a_3\) +... + a has n terms and is a finite series with n terms.
As a result, \(S_n\) is used to represent the series' sum as follows:
\(S_n\)=∑ \(a_n\)
Given:
1 + x + x² + x³ + \(x^4\) + \(x^5\) + ⋯ + \(x^{100\)
let P= 1/ 1-x
P - Px= 1
P= 1+ Px
= 1 + (P)x
= 1 + (1+ Px) x
= 1+ x + Px²
= 1+ x + (1+ Px)x²
= 1+ x + x² + Px³ and so on
So, 1+ x² + x³ + \(x^4\) + \(x^5\) + ⋯ + \(x^{100\) = \(\sum^{100} _ {n=0}\) 1/( 1- x)
Learn more about series here:
https://brainly.com/question/23280277
#SPJ1
Let a, β, y be the three interior angles of any triangle, and try to prove that cos(a+β+y) = -1.
\(prove \: that \: \cos( \alpha + \beta + \gamma ) = - 1\)
Answers
Given:
\(\alpha, \beta, \gamma\) are three interior angles of any triangle.
To prove:
\(\cos (\alpha+\beta+\gamma)=-1\)
Solution:
According to the angle sum property of a triangle, the sum of all three interior angle of a triangle is always 180 degrees.
It is given that, \(\alpha, \beta, \gamma\) are three interior angles of any triangle.
Using the angle sum property of triangles, we get
\(\alpha+\beta+\gamma =180^\circ\) ...(i)
We need to prove,
\(\cos (\alpha+\beta+\gamma)=-1\)
Taking LHS, we get
\(LHS=\cos (\alpha+\beta+\gamma)\)
\(LHS=\cos (180^\circ)\) [Using (i)]
\(LHS=-1\)
\(LHS=RHS\)
Hence proved.
4. If -24 = -5n +1, then-3n=
?
Answers
Answer:
Step-by-step explanation:
-5n + 1 = -24
-5n = -25
n = 5
-3(5)= -15
Step-by-step explanation:
-5n+1 = -24
-5n = -25
n = 5
-3n = 5*-3
-3n = -15
Most everyday purchases at the store are labeled with the price of the item before sales tax. Which expression could
be used to find the amount of tax?
Amount of Tax = Original Price + Total Cost
Amount of Tax = (Total Cost)(Original Price)
O Amount of Tax = (Original Cost)(Tax %)
Amount of Tax = (Total Cost)(Tax %).
Answers
Answer:
the answer is c.
just the answered the question and it was correct on edg
Answer:
They are correct its C.
Step-by-step explanation:
Fabian says that 25% of a number will always be greater than 10% of any other number.
Complete one inequality to support Fabian's claim and one to show that he is incorrect.
Answers
The claim that is being made by Fabian is wrong and this can be proven by the steps below.
What is percentage of a number?The percentage of a number is the part of the number that is being represented by per hundred when it is divided by the whole and multiply by 100.
The 25% of a number can not always be greater than the 10% of any other number and this can be proven by using two different numbers.
For example, the 25% of 150 = 25/100 ×150 = 3750/100
= 37.5
Using another number such as 1500, the 10% of the given number is calculated as follows:
10/100 × 1500 = 15000/100 = 150
From the given examples, the 25% of 150 is not greater than the 10 percent of 1500, therefore, 25% of a number can not always be greater than the 10% of any other number and this can be proven by using two different numbers.
Learn more about percentage here:
https://brainly.com/question/24304697
#SPJ1
Please answer this before friday
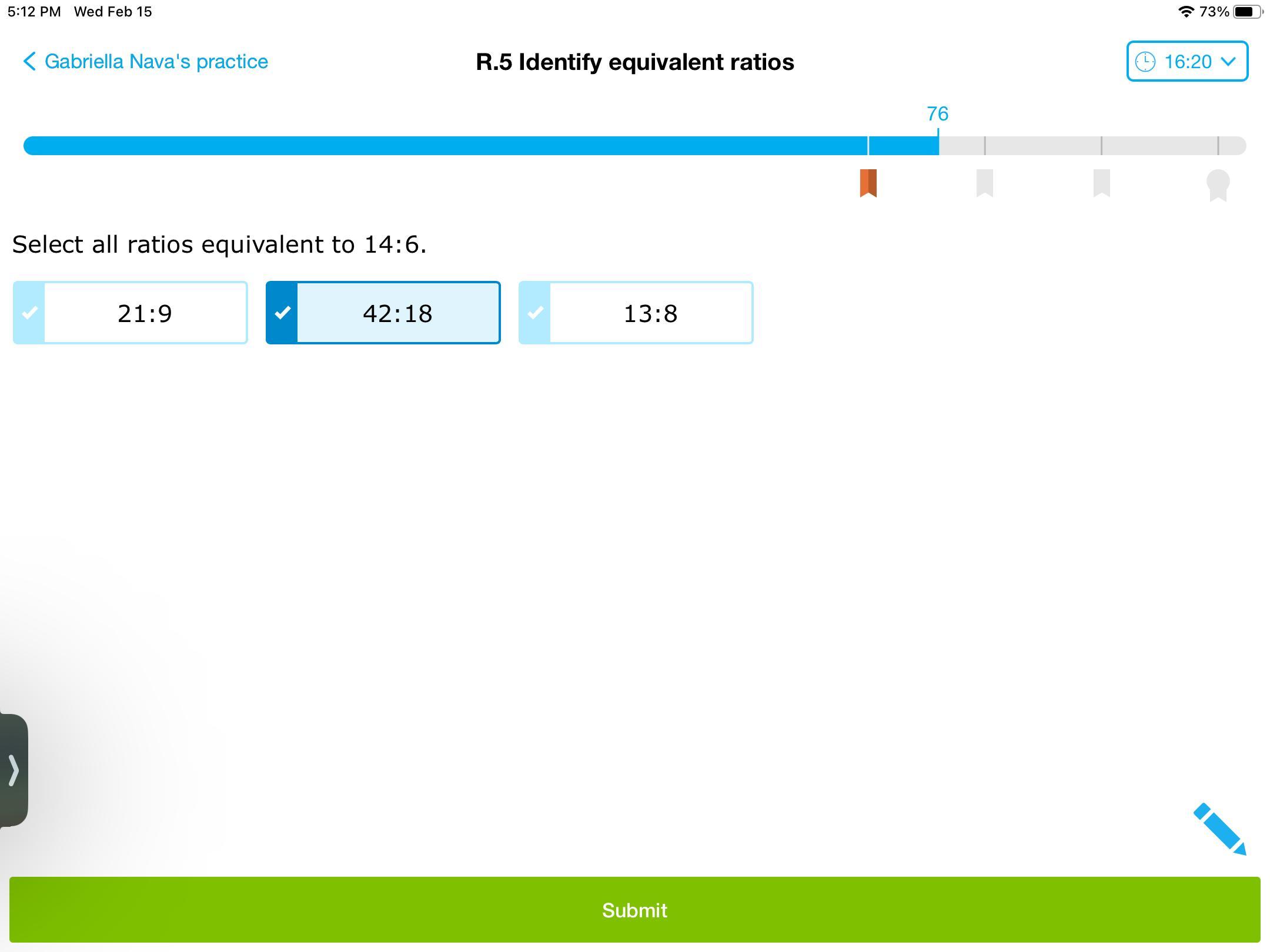
Answers
Answer: 21:9 and 42:18
Step-by-step explanation:
14:6 at its most basic form is 7:3, so find anything that could be equal to this if a number is multiplied on both sides.
21:9 is our simplified ratio multiplied by 3 on both sides.
42:18 is our simplified ratio multiplied by 6 on both sides.
But, the final ratio doesn't work, because 7 and 3 respectively cannot multiply to 13 and 8 with the same value.
weekand homework and i need help
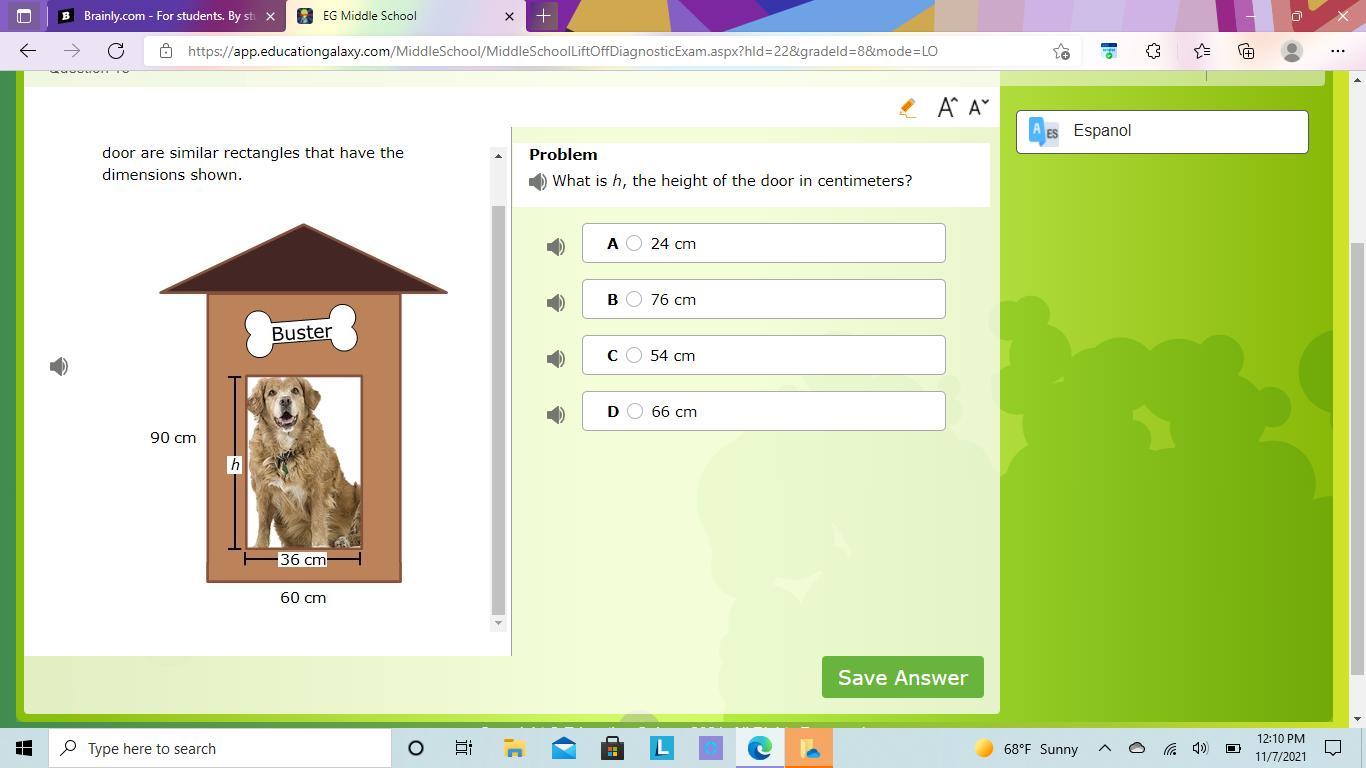
Answers
Answer:
C. 54
Step-by-step explanation:
36/60=.6
90*.6=54
Answer:
1 got C.
60/36=1.66666667
60/(5/3)=36
90/(5/3)=54
What is the meaning of "if \(\varphi (x)\) has no parameters \(p_{i}\) then the class C is definable"?
![What is the meaning of "if [tex]\varphi (x)[/tex] has no parameters [tex]p_{i}[/tex] then the class C](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/yxAwmsaXJBUQhpdRbSM40V2ZzqIoance.png)
Answers
The meaning of the statement, "if the function has no parameters, then the class C is definable" is that if there are no parameters given then the class c can be defined with an empty set but if there are no parameters, then the class cannot be defined.
What is the meaning of the statement?The meaning of the above statement is that if no parameters are provided for this function, then the given class represented as c can be defined with an empty set that is enclosed in parameters.
Also, if the parameters are given then the class c is not defined.
Learn more about defining functions here:
https://brainly.com/question/11624077
#SPJ1
Question 3 (2 points)
Cars-2-Go rents out cars for a $23.75 rental fee and charges $.35 per mile. Which function rule matches this situation when x = number of
miles and y = total cost?
Answers
Answer:
23.75+0.35x=Y
Step-by-step explanation:
It starts at $23.75. $0.35 is per mile so that means it will have an x. Add the two up and it is y.
Two boards are placed end to end to make a walkway. One board is 6 feet 11 inches long, and the other board is 5 feet 7 inches long. How long is the walkway?
Write your answer in feet and inches. Use a number less than 12 for inches.
Answers
The walkway is 11 feet 6 inches long.
To find the length of the walkway, we need to add the lengths of the two boards.
The first board is 6 feet 11 inches long, which can be written as 6 + 11/12 feet using the fact that there are 12 inches in a foot.
The second board is 5 feet 7 inches long, which can be written as 5 + 7/12 feet.
Now we can add the lengths of the two boards:
6 + 11/12 feet + 5 + 7/12 feet
= 11 + 6/12 feet
=11 + 1/2 feet
Therefore, the walkway is 11 feet 6 inches long.
To learn more on Coordinate Geometry click:
brainly.com/question/27326241
#SPJ1
Write an equation for the following scenario:
Small whiteboards cost $15 each with a $20 delivery fee for the entire order, regardless of size.
Answers
Explication:
Patrick managed to sell the 20th most bicycles last year of all the salespeople at the company.He also managed to sell the 20th least bicycles last year of all the salespeople at that company.How many salespeople were there at that company?Assume that no one sold the same number of bicycles than another
Answers
definitely missing a number so it's prolly something like
a/20=20
sorry if this doesn't help you didn't give us much to work on
Plz helppppppppppppp

Answers
Answer:
LK = 7 as this is a 45-45-90 Triangle
Step-by-step explanation:
Hello! To begin answering this question, one must understand that angle the Pythagorean Theorem applies here! Hypotenuse squared = leg squared + leg squared, (7 square root of 2)^2 = 7^2 + X^2, 7^7 + 7^7 = (7 square root of 2)^2, 98 = 98.
Answer:
Step-by-step explanation:
Evaluate the following algebraic expressions by substituting z raised to the second power where z=7
Answers
Answer:
49
Step-by-step explanation:
z=7 which means that 7 raised to the second power is 7 multiplied by itself. When you do 7 x 7 your answer will be 49. Hope that helps :)
what are the ratios from least to greatest 5:8, 11:16, 18:32
Answers
Answer:
Least: 18:32
Middle: 5:8
Greatest: 11:16
What type of association does the graph show?
A. positive nonlinear
B. positive linear
C. negative nonlinear
D. negative linear

Answers
Answer:
B. Positive linear
Step-by-step explanation:
First, this graph is a linear graph because a linear graph is a straight line. The graph in the diagram is also a straight line, so it is linear.
Also, notice how as x increases, y increases. This means that the graph is positive
I have to solve and round to the nearest tenth

Answers
Answer:
approximately 5.6
Step-by-step explanation:
Cross multiply
16a=90
a=5.625
Please helppppppp meeee

Answers
The range, given the cost of surfboard rentals, would be $ 140.
The interquartile range of the cost of surfboard rentals is $ 56.
There is an outlier which is the cost of 6 days of rentals which is $ 168.
How to find the range and interquartile range ?To find the range, the formula is :
= Largest cost - Lowest cost
To find these costs, find the cost of the days of rentals :
1 day : 2 days 3 days :
= 28 x 1 = 28 x 2 = 28 x 3
= $ 28 = $ 56 = $ 84
6 days :
= 28 x 6
= $ 168
The range is therefore :
= 168 - 28
= $ 140
To find the Interquartile range, first find the First Quartile and the Third Quartile after ordering the costs:
Order of costs :
28, 28, 28, 56, 56, 56, 84, 84, 84, 168
First quartile position :
= 1 / 4 x ( n + 1 )
= 1 / 4 x ( 10 + 1 )
= 3 rd position which is $ 28
Third quartile position :
= 3 / 4 x ( n + 1 )
= 3 / 4 x ( 10 + 1 )
= 8 th position which is $ 84
The Interquartile range is :
= 84 - 28
= $ 56
The outlier is the cost of 6 days which is $ 168. This is a rental as it is much larger than other costs.
Find out more on outliers at https://brainly.com/question/29546240
#SPJ1
Three quarters of a number is 27. What is two ninths of the number?
Answers
Answer:
8
Step-by-step explanation:
let x be the number , then
\(\frac{3}{4}\) x = 27 ( multiply both sides by 4 to clear the fraction )
3x = 108 ( divide both sides by 3 )
x = 36
the number is 36, so
\(\frac{2}{9}\) × 36 = 2 × 4 = 8
The two ninths of the number is 8
We know that Three quarters of a number is \(\frac{3}{4}\) times of a number
Hence we will assume the number x ,
\(\frac{3}{4} of x = 27\)
\(x = 27 X \frac{4}{3}\)
\(x = 36\)
Now as we know the number is 36
Therefore , the two ninths of the number assumed as y
We will multiply the number 36 by 2 and then divide by 9
Hence,
\(y = 36 X \frac{2}{9}\)
\(y = 8\)
Thus, the two ninths of the number 36 is 8
Practice more quarters related questions
https://brainly.in/question/13325111