The average amount of money a person spends on lottery tickets each month is €6. By looking at the data set, a Poisson discrete distribution is assumed for this variable. Calculate each of the following.
a. The probability of buying no lottery ticket.
b. The probability of buying 1 lottery ticket.
c. The probability of buying 2 lottery tickets.
d. The probability of buying fewer than or equal 3 tickets.
Answers
(a) Probability of buying no lottery ticket is 0.002478. (b) Probability of buying 1 lottery ticket is 0.014870. (c) Probability of buying 2 lottery tickets is 0.089221. (d) Probability of buying fewer than or equal to 3 tickets can be obtained by adding the respective probabilities.
The probability of buying no lottery ticket can be calculated using the Poisson distribution formula, where the mean (λ) is equal to the average amount spent on lottery tickets per month, which is €6.
P(X = 0) = (e^(-λ) * λ^0) / 0!
P(X = 0) = e^(-6) * 6^0 / 0!
Since 0! = 1, the probability of buying no lottery ticket is:
P(X = 0) = e^(-6) ≈ 0.002478
(b) The probability of buying 1 lottery ticket can be calculated similarly:
P(X = 1) = (e^(-λ) * λ^1) / 1!
P(X = 1) = e^(-6) * 6^1 / 1!
Since 1! = 1, the probability of buying 1 lottery ticket is:
P(X = 1) = 6 * e^(-6) ≈ 0.014870
(c) The probability of buying 2 lottery tickets:
P(X = 2) = (e^(-λ) * λ^2) / 2!
P(X = 2) = e^(-6) * 6^2 / 2!
Since 2! = 2, the probability of buying 2 lottery tickets is:
P(X = 2) = (36 * e^(-6)) / 2 ≈ 0.089221
(d) The probability of buying fewer than or equal to 3 tickets can be calculated by summing the probabilities of buying 0, 1, 2, and 3 tickets:
P(X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
Using the values calculated in parts (a), (b), and (c), we can find:
P(X ≤ 3) ≈ 0.002478 + 0.014870 + 0.089221 + P(X = 3)
The value of P(X = 3) can be calculated using the Poisson distribution formula in a similar manner.
Therefore, the probability of buying fewer than or equal to 3 lottery tickets can be obtained by adding up the probabilities calculated for each specific case.
To learn more about Poisson distribution formula click here
brainly.com/question/30388228
#SPJ11
Related Questions
One independent survey showed that 70% on people asked like coffee. Another independent survey showed that 80% of people like tea. What is the upper and lower bound of peoples who likes both coffee and tea?
Answers
The range of people who like both coffee and tea is between 75% and 75%, with the total number of people who like both being 75%.
If 70% of people like coffee, and 80% of people like tea, the minimum number of people who like both coffee and tea is the smaller percentage, which is 70%. The maximum number of people who like both coffee and tea is the smaller of the two percentages, which is 80%.
Therefore, the range of people who like both coffee and tea is 70% to 80%.
To calculate the actual range, you must first calculate the difference between the two percentages:80% - 70% = 10%
Then divide that difference by 2 and subtract and add it to the smaller number:
10% ÷ 2 = 5%
Lower bound: 70% + 5% = 75%
Upper bound: 80% - 5% = 75%
To know more about range visit:-
https://brainly.com/question/29204101
#SPJ11
Find the domain of the equation.
ln\(\frac{x^3+5x^2+3x-9}{x^2-x-2}\)
Answers
The domain of the rational function \(\frac{x^3 + 5x^2 + 3x - 9}{x^2 -x - 2}\) is:
D: {x ∈ R| x ≠ -1, 2}
How to find the domain?The domain will be the set of all real numbers, minus these ones that make the denominator equal to zero.
The denominator will be zero when:
x² - x - 2 =0
Using the quadratic formula we will get:
\(x = \frac{1 \pm \sqrt{(-1)^2 - 4*1*-2} }{2*1} \\\\x = \frac{1 \pm 3}{2}\)
The two solutions are:
x = (1 + 3)/2 = 2
x = (1 - 3)/2 = -1
If the numerator is not zero on these values, then we need to remove them from the domain.
When x = 2 the numerator is:
2³ + 5*2² + 3*2 - 9 = 25
When x = -1
(-1)³ + 5*(-1)² + 3*-1 - 9 = -8
Neither of these is zero, so we need to remove x = -1 and x = 2 from the domain, then the domain is:
D: {x ∈ R| x ≠ -1, 2}
Learn more about rational functions:
https://brainly.com/question/1851758
#SPJ1
3 pounds of apples cost $8.37 how much each pound
Answers
Answer:
$2.79 per pound of apple.
Step-by-step explanation:
\(\frac{3}{8.37}=\frac{1}{x}\)
\(3x = 8.37\)
\(x = 2.79\)
The standard form for a parabola with vertex (h,k) and an axis of symmetry of x=h is:(x-h)^2=4p(y-k)The equation below is for a parabola. Write it in standard form. When answering the questions type coordinates with parentheses and separated by a comma like this (x,y). If a value is a non-integer then type is a decimal rounded to the nearest hundredth. 5x^2-50x-4y+113=0 The value for p is: AnswerThe vertex is the point: AnswerThe focus is the point: AnswerThe directrix is the line y=Answer
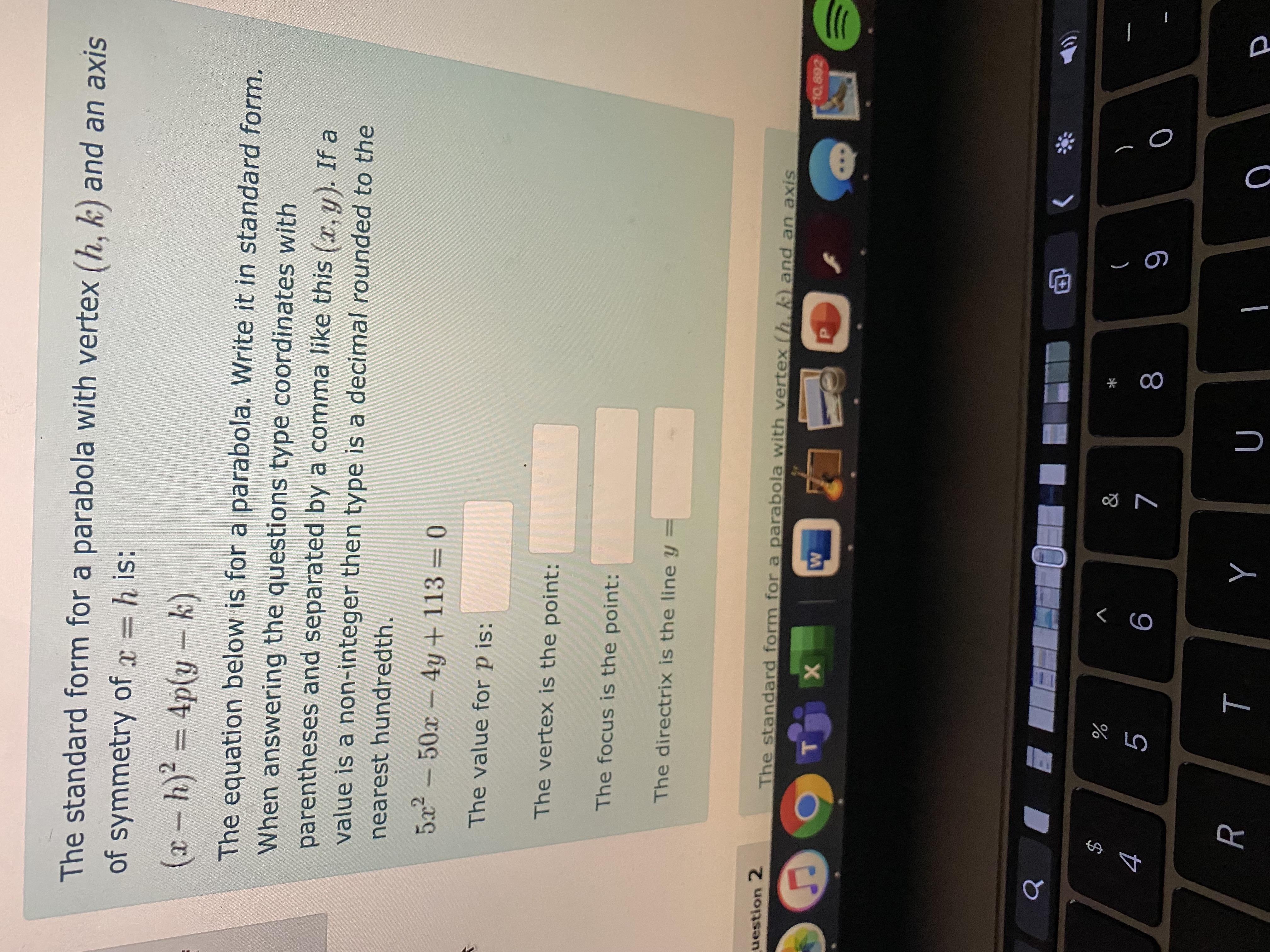
Answers
Given the equation of a parabola:
\(5x^2-50x-4y+113=0\)• You can rewrite it in Standard Form by following these steps:
1. Add the y-term to both sides of the equation:
\(\begin{gathered} 5x^2-50x-4y+113+(4y)=0+(4y) \\ \\ 5x^2-50x+113=4y \end{gathered}\)2. Subtract the Constant Term from both sides of the equation:
\(\begin{gathered} 5x^2-50x+113-(113)=4y-(113) \\ \\ 5x^2-50x=4y-113 \end{gathered}\)3. Divide both sides of the equation by 5 (the leading coefficient)
\(x^2-10x=\frac{4}{5}y-\frac{113}{5}\)4. The coefficient of the x-term is:
\(b=-10\)Then, you need to add this value to both sides:
\((\frac{-10}{2})^2=5^2\)Therefore.
\(\begin{gathered} x^2-10x+5^2=\frac{4}{5}y-\frac{113}{5}+5^2 \\ \\ x^2-10x+5^2=\frac{4}{5}y+\frac{12}{5} \end{gathered}\)5. Rewrite the equation as follows:
\(\begin{gathered} (x-5)^2=\frac{4}{5}(y+3) \\ \\ (x-5)^2=0.8(y+3) \end{gathered}\)• Having the equation written in Standard Form:
\((x-h)^2=4p(y-k)\)You can identify that:
\(4p=\frac{4}{5}\)Solving for "p", you get:
\(p=\frac{4}{5\cdot4}=\frac{1}{5}=0.2\)• You can identify that:
\(\begin{gathered} h=5 \\ k=-3 \end{gathered}\)Therefore, the Vertex is:
\((5,-3)\)• By definition, the Focus of a parabola that opens upward is given by:
\((h,k+p)\)Then, in this case, this is:
\((5,-3+0.2)=(5,-2.8)\)• By definition, the Directrix for a parabola that opens upward is given by:
\(y=k-p\)Then, in this case, you get:
\(\begin{gathered} y=-3-0.2 \\ \\ y=-3.2 \end{gathered}\)Hence, the answers are:
• Standard Form:
\((x-5)^2=0.8(y+3)\)• Value for "p":
\(p=0.2\)• Vertex:
\((5,-3)\)• Focus:
\((5,-2.8)\)• Directrix:
\(y=-3.2\)
6,402.66 divided by 459438.26
Answers
Answer: 0.0139358
Step-by-step explanation: 999,999,999,999,999,999,999,999,999,999,999% sure!
What is the product?
-1
со то
-5
-32
4
o
20
-36
32
-4
O
-20

Answers
Answer:
A
Step-by-step explanation:
Multiply the number by every element of the matrix. Answer: A
Try and explain this lol
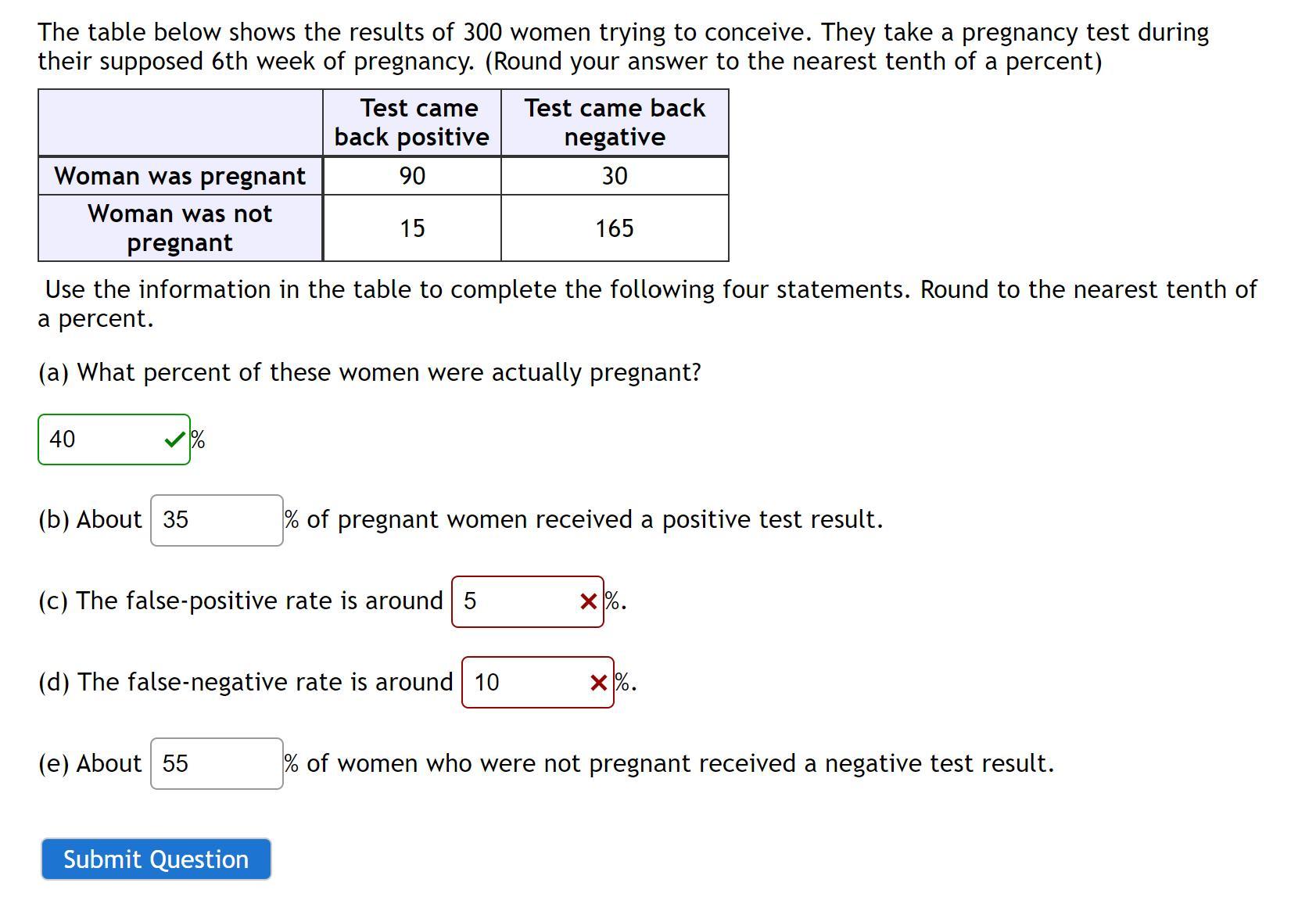
Answers
The answer to all the questions is illustrated below.
What is the percentage?A percentage is a value per hundredth. Percentages can be converted into decimals and fractions by dividing the percentage value by a hundred.
From the given information,
a. The percentage of women actually pregnant is,
= [(90 + 30)/300]×100%.
= (120/300)×100%.
= 40%.
b. The percentage of women who received a positive result is,
= [(90 + 15)/300]×100%.
= [105/300]×100%.
= 35%.
c. The false positive rate is,
= (15/105)×100%.
= 14%.
d. The negative-positive rate is,
= (30/195)×100%.
= 15%.
e. The percentage of women who were not pregnant received a negative test result is,
= (30/195)×100%.
= 15%.
Learn more about percentages here :
https://brainly.com/question/24159063
#SPJ1
Is 48.4 closest to 49 on a number line
Answers
Answer:
if there are any less than 4.84 then yes it is.
Step-by-step explanation:
please give brainliest and hope this helps
On a zip-line course, you are harnessed to a
cable that travels through the treetops. You
start at platform A and zip to each of the other
platforms. How far do you travel from Platform
B to Platform C?

Answers
Using the distance between two points, it is found that you travel approximately 41 meters.
What is the distance between two points?Suppose that we have two points, \((x_1,y_1)\) and \((x_2,y_2)\). The distance between them is given by:
\(D = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
In this problem, we have that:
The coordinates of B are (-25,-25).The coordinates of C are (-15,15).Hence the distance is:
D = sqrt[(-15 - (-25))² + (15 - (-25))²] = sqrt(10² + 40²) = 41 meters.
More can be learned about the distance between two points at https://brainly.com/question/18345417
#SPJ1
How do we calculate using the column method
\( 274561 + 367238\)
![How do we calculate using the column method[tex] 274561 + 367238[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/T8yWyQ6ylPkZC9T0lXpDFm1Lgn6XiprH.jpeg)
Answers
Answer:
641799
Step-by-step explanation:
274561
+367238
641799
Using the table below, which are ordered pairs of points that can be plotted to graph
Help me aspp please thank you

Answers
Ordered pairs of points that can be plotted to graph are (-1,1),(1,5).
The correct option is (b).
What is graph?A graph is a structure made up of a collection of things where some object pairs are conceptually "connected." Each pair of connected vertices is known as an edge, and the items are represented by mathematical abstractions called vertices (also known as nodes or points) (also called a link or line). In a diagram, a graph is often represented by a group of dots or circles for the vertices and lines or curves for the edges. Graphs are one of the subjects covered in discrete mathematics. Both directed and undirected edges are possible. The fundamental topic of graph theory is graphs.
Calculation:
We have to find the ordered pair of points that can be plotted to graph of 6x - 3y = -9
By putting x = -1
⇒ -6 - 3y = -9
⇒ 3 = 3y
⇒ y = 1
By putting x = 0
⇒ -3y = -9
⇒ y = 3
By putting x = 1
⇒ 6 - 3y = -9
⇒ 15 = 3y
⇒ y = 5
So, the ordered pairs obtained are (-1,1),(0,3) and (1,5).
Hence, the correct option is (b)
To learn more about Graph, visit:
brainly.com/question/19040584
#SPJ1
4x2 - 7 + 2x - 3x² + 8x - 6
Answers
Answer:
(4x2 - 2x) - (-5x2 - 8x)
= 4x2 - 2x + 5x2 + 8x.
= 4x2 + 5x2 - 2x + 8x.
= 9x2 + 6x.
= 3x(3x + 2).
Answer: 3x(3x + 2)
Step-by-step explanation:
Lucas spends $83.42 in additional interest and charges on monthly payments as the result of a prior bankruptcy. if lucas been able to save this money for the year and then put it into a savings account earning 1.8% simple interest, how much money could he have in savings after 3 more years? a. $1,649.72 b. $1,055.10 c. $1,019.06 d. $1,001.04
Answers
The total amount Lusac have in his savings after 3 more years with 1.8% saving interest is $1055.10.
What is simple interest?Simple interest is the amount charged on the principal amount with a fixed rate of interest for a time period. Simple interest calculated only on the principal amount.
The formula for the simple interest can be given as,
\(I=\dfrac{Prt}{100}\)
Here, (I) is the interest amount earned on the principal amount of (P) with the rate of (r) in the time period of (t).
Lucas spends $83.42 in additional interest and charges on monthly payments as the result of a prior bankruptcy. The amount save in a year (12 months) is,
\(P=83.42\times12\\P=1001.04\)
The interest earned on this principal amount with earning 1.8% simple interest, after 3 years is,
\(I=\dfrac{1001.04\times1.83}{100}\\I=54.06\)
The total total amount in his bank account after 3 years is,
\(A=P+I\\A=1001.04+54.06\\A=1055.10\)
Hence, the total amount Lusac have in his savings after 3 more years with 1.8% saving interest is $1055.10.
Learn more about the simple interest here;
https://brainly.com/question/2294792
Answer:
b.
$1,055.10
Step-by-step explanation:
right on edg 22
In the number 707B47.B is a prime number.If the number is rounder off to 3sf its value is 708000 what is the biggest value of B
Answers
The list of single digit primes is {2,3,5,7}. The largest prime is 7, so B = 7 is the largest possible value.
Also note how 707,747 rounds to 708,000 when rounding to 3 significant figures.
Write the mathematical model and use Solver to answer the following question:
A farm co-op has 6,000 acres available to plant with corn and soybeans. Each acre of corn requires 9 gallons of fertilizer/herbicide and 0.75 hour of labor to harvest. Each acre of soybeans requires 3 gallons of fertilizer/herbicide and 1hour of labor to harvest. The co-op has available at most 40,501 gallons of fertilizer/herbicide and at most 5,250 hours of labor for harvesting. Find the maximum profit if the profits per acre are $75 for corn and $40 for soybeans. Round your answer to the nearest cent if necessary.
a. $210,000.00
b. $393,750.00
c. $371,255.83
d. $180,004.44
e. $318,744.17
Answers
The maximum profit if the profits per acre are $75 for corn and $40 for soybeans is $371,255.83. Therefore, the correct option is c.
To find the maximum profit from planting corn and soybeans, we can use linear programming. Let's first define the variables and write the constraints.
Let x be the number of acres of corn and y be the number of acres of soybeans.
1. Total acre constraint: x + y ≤ 6,000
2. Fertilizer/herbicide constraint: 9x + 3y ≤ 40,501
3. Labor constraint: 0.75x + y ≤ 5,250
The objective function to maximize is the profit function: P(x,y) = 75x + 40y
Now, we will use the Solver to find the maximum profit:
Step 1: Set up a spreadsheet with the constraints and the objective function.
Step 2: Go to the Data tab and click on Solver. If Solver is not available, you may need to add it in Excel Options.
Step 3: Set the objective function by selecting the cell with the profit function.
Step 4: Choose "Max" for the objective.
Step 5: Add the constraints by selecting the corresponding cells.
Step 6: Click on "Solve" and the Solver will find the optimal values for x and y.
After using Solver, we find that the optimal values are x = 4,363.89 (corn) and y = 1,636.11 (soybeans), which yields a maximum profit of $371,255.83. Therefore, the correct answer is c: $371,255.83
Learn more about Linear programming:
https://brainly.com/question/14309521
#SPJ11
A sealed-beam headlight is in the shape of a paraboloid of revolution. The bulb, which is placed at the focus, is 1 inch from the vertex. If the depth is to be 2 inches, what is the diameter of the headlight at its opening?
Answers
The diameter of the headlight's opening is 4 inches.
To find the diameter of the headlight's opening, we need to determine the distance between the two points on the paraboloid where the depth is 2 inches.
Using the formula for the paraboloid of revolution, we know that the equation for the shape of the headlight is:
\(y^2 = 4px\)
where p is the distance from the vertex to the focus. In this case, p = 1 inch.
To find the distance between two points on the paraboloid where the depth is 2 inches, we can set y = ±2 and solve for x:
\(4p^2 = 4x(\pm2)\\x = p^2/\pm1\)
Since we're interested in the distance between two points, we can subtract the two x-values:
\(x^2 - x^1 = p^{2/1} - p^{2/-1}\\x^2 - x^1 = 2p^2\)
Substituting in the value of p, we get:
x2 - x1 = 2(1^2) = 2
So the distance between the two points where the depth is 2 inches is 2 inches.
To find the diameter of the headlight's opening, we need to double this distance and then multiply by the focal length:
d = 2(2)(1) = 4 inches
Therefore, the diameter of the headlight's opening is 4 inches.
learn more about diameter
https://brainly.com/question/30428141
#SPJ11
Write the equation of a line that contains the given point and has the given slope:
(-8,-8), slope is 3
Answers
Answer:
Ok
Step-by-step explanation:
Y = mx + c
Slope is for the gradient =m therefore we have +3 as our gradient
Now we are going to substitute pont - 8mac- 8 on the above equation
Y = mx +c
-8=3(-8) +c
-8=-24 +c
-8+24 =c
16=c
This means that the y intecept of this straight line is 0 mac 16
Meaning that when the line touches the y axis at 16 x will be equal to zero
Therefore our equation is
Y =3x +16
PLZZZZZZZZZZZZZZZZZZZZZ:( PLZZZZZZZZ

Answers
Answer:
12.57
Step-by-step explanation:
The frequency tables shows the results of tossing a ball 24 times into the four colored sections on a carnival game . based on the data table , how many will the ball most likely land in the yellow section
Answers
Answer:
Step-by-step explanation:
Answer is 65 simple
Is the number -22 an integer?
Answers
Answer:
Yes
Step-by-step explanation:
Any whole number is an integer.
Yes, because any whole number, positive or negative, is an integer.
HELPP PLSSSS NO BOTS OR I WILL REPORT!!!

Answers
Answer:
B. false
Step-by-step explanation:
if the area of a circle is 153.86m find diamiter and perimeter
Answers
Answer:
the diameter is 14 and the perimeter is 43.97
In a binomial situation, n=18 and π=0.60. Determine the expected
value
Answers
The expected value in a binomial situation with n = 18 and π = 0.60 is E(X) = np = 18 * 0.60 = 10.8.
In a binomial situation, the expected value, denoted as E(X), represents the average or mean outcome of a random variable X. It is calculated by multiplying the number of trials, denoted as n, by the probability of success for each trial, denoted as π.
In this case, we are given n = 18 and π = 0.60. To find the expected value, we multiply the number of trials, 18, by the probability of success, 0.60.
n = 18 (number of trials)
π = 0.60 (probability of success for each trial)
To find the expected value:
E(X) = np
Substitute the given values:
E(X) = 18 * 0.60
Calculate the expected value:
E(X) = 10.8
learn more about binomial here:
https://brainly.com/question/31049218
#SPJ4
∠A and ∠B are adjacent. The sum of their measures is 92°. ∠A measures (2x+5)°. ∠B is three times the size of ∠A.
Write an equation to determine the value of x. Then solve your equation and find the measures of both angles.
Enter the correct answers in the box.
Answers
The equation use to determine the value of \(x\) is \((2x+5)+3(2x+5)=92\).
The measures of \(\angle A, \angle B\) are \(23^\circ, 69^\circ.\)
Let us assume the measures of \(\angle A, \angle B\) are \(z, y\).
Now according to the question, we can write the relation between \(\angle A, \angle B\) is \(y=3z....(i)\).
We know, the measure of \(\angle A\) is \(2x+5\) so \(2x+5=z....(ii)\). Now, we will substitute the value of \(z\) from equation \((ii)\) in equation \((i)\).
\(y=3z\\= 3 \times (2x+5)\\=6x+15\)
So, the final equation will be \((2x+5)+3(2x+5)=92\)
⇒ \(6x+15+2x+5=92\)
⇒ \(8x+20=92\)
⇒ \(8x=72\)
⇒ \(x=9\)
\(\therefore\) measure of \(\angle A\) is \(2x+5=(2 \times 9)+1=25\) and measure of \(\angle B\) is \(2 \times 23 = 69\).
To learn more about Adjacent angles
https://brainly.com/question/26768295
https://brainly.com/question/29228976

HELP!!! answer quickly pls

Answers
The first one B
Step by step explanation:
B is (2,4) then do 2+1 which is 3 and then 4 -3 which is 1 and your left with (3,1) which is point B
If A and B are two subsets of with n() = 43, n(A) = 25, n(B) = 18 and n(AB) = 7, which is the value of n(AUB).
Answers
Answer: We can use the following formula for the union of two sets:
n(A U B) = n(A) + n(B) - n(A ∩ B)
where n(A ∩ B) is the number of elements in the intersection of A and B.
Substituting the given values, we get:
n(A U B) = n(A) + n(B) - n(A ∩ B)
n(A U B) = 25 + 18 - 7
n(A U B) = 36
Therefore, the value of n(A U B) is 36.
figure is made from a part of a square and a part of a circle.
$
This figure
10
a) What is the perimeter of this
figure, to the nearest unit?
Answers
Answer:
Step-by-step explanation:
Answer:38
Step-by-step explanation:
find the average speed of a world-class sprinter (to the nearest tenth) if he runs 100 yards in 10 sec
Answers
The Average speed of a world class sprinter, is he runs 100 yards in 10 sec is 36 km/h.
If an athlete can run 100 meters in 10 seconds, It is said that he cannot run 10 meters in one second. That may also apply to the physical world we live in. But you clearly state that you want to say mathematically whether he ran 10 meters in his 1 second.
If a sprinter runs 100 meters in 10 seconds, then, First, we need to convert meters to kilometers and seconds to hours. 1 meter = 1/1000 kilometers 100 meters = 100/1000 kilometers = 1/10 = 0.1 kilometers 1 second = 1/3600 hours 10 seconds = 10/3600 = 1/360 hours.
Now,
According to the question:
Given that,
Distance covered by sprinkler = 100m
Time taken by sprinkler = 10 seconds
Using the equation of velocity
Distance/ Time = velocity
Now, substituting the values -
= 100/10
= 10
Thus, the velocity is 10m/s
To convert it into m/s in to km/h -
= (10/1000) x 3600
= 36000/1000
= 36
Therefore, The average velocity of sprinkler is 36 km/h
Learn more about Average Velocity:
https://brainly.com/question/29125647
#SPJ4
find an equation for the line that passes through the points (-6,-5) and (6,4)
Answers
\((\stackrel{x_1}{-6}~,~\stackrel{y_1}{-5})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{4}-\stackrel{y1}{(-5)}}}{\underset{run} {\underset{x_2}{6}-\underset{x_1}{(-6)}}} \implies \cfrac{4 +5}{6 +6} \implies \cfrac{ 9 }{ 12 } \implies \cfrac{3 }{ 4 }\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-5)}=\stackrel{m}{ \cfrac{3 }{ 4 }}(x-\stackrel{x_1}{(-6)}) \implies y +5 = \cfrac{3 }{ 4 } ( x +6) \\\\\\ y+5=\cfrac{3 }{ 4 }x+\cfrac{9}{2}\implies y=\cfrac{3 }{ 4 }x+\cfrac{9}{2}-5\implies {\Large \begin{array}{llll} y=\cfrac{3 }{ 4 }x-\cfrac{1}{2} \end{array}}\)
Answer:
\(\displaystyle \boxed{ y=\frac{3}{4}x-\frac{1}{2} }\)
Step-by-step explanation:
First, we will find the slope. This is done by finding the change in y over the change in x.
\(\displaystyle \frac{y_{2} -y_{1} }{x_{2} -x_{1} }= \frac{4--5}{6--6} =\frac{4+5}{6+6}=\frac{9}{12}=\frac{3}{4}\)
Next, we will find the equation. We will create a point-slope equation and simplify into slope-intercept form.
y - 4 = \(\frac{3}{4}\)(x - 6)
y = \(\frac{3}{4}\)x - \(\frac{9}{2}\) + 4
y = \(\frac{3}{4}\)x - \(\frac{1}{2}\)

How are the properties of exponents used when dividing a polynomial by a monomial?
Answers
Use the rules of exponents to divide variables with the same base when dividing monomials. According to this rule, the base should remain in the position (numerator or denominator) where the greater exponent was when dividing variables with the same base after the exponents have been subtracted.
What additional factor is utilised to divide a monomial by a monomial?In order to divide a polynomial by a monomial, let's first divide a monomial by another monomial. The monomial should be divided into numerical and variable factors. By deducting the exponents of each y term, divide the coefficients and variables.
What comes first in the polynomials by monomial division?Let's go over the three steps that must be completed in order to divide a polynomial by a monomial. Rewrite the issue and divide each polynomial term by the monomial as a first step. Dividing the numbers is the next step. Divide the variables is the third and last stage.
To know more about exponents visit:-
brainly.com/question/5497425
#SPJ1