The Burns family went to breakfast at Huddles House. Mr. Burns ordered a meal for $7.75. Mrs. Burns ordered a meal for $9.50. The four kids ordered kids meals for $3.49 each. They left a 20% tip. How much was the bill (excluding tax)?
A
$6.24
B
$31.21
C
$37.45
D
$24.97
Answers
Answer:
The bill was C) 37.452
The awesome math I did:
7.75+9.50+(3.49*4)
7.75+9.50+13.96
31.21 that times 0.20 is 6.24
31.21+6.24 = 37.45
Related Questions
prove the identity tan3x-tanx =2sinxsec3x
Answers
(Problem #1) 2sin(x)/cos(3x) = tan(3x) - tan(x)
Let's try to prove that 2sin(x) = sin(3x) - tan(x)cos(3x).
Using the identities sin(3x) ? 3sin(x) - 4sin³(x) and cos(3x) ? 4cos³(x) - 3cos(x),
sin(3x) - tan(x)cos(3x) = 3sin(x) - 4sin³(x) - tan(x)(4cos³(x) - 3cos(x))
= sin(x)(3 - 4sin²(x) - (4cos²(x) - 3))
= sin(x)(6 - 4(sin²(x) + cos²(x)))
= 2sin(x).
(The above is simpler than using the standard identity that gives tan(3x) in terms of tan(x).)
(Problem #2) (1 - tan²((?/4)-x))/(1 + tan²((?/4)-x)) = sin(2x)
Multiplying the numerator and denominator of the left-hand side by cos²((?/4)-x)) gives
(cos²((?/4)-x)) - sin²((?/4)-x)))/(cos²((?/4)-x)) + sin²((?/4)-x))),
which equals cos(2(?/4 - x))/1, i.e., cos(?/2 - 2x), i.e., sin(2x).
(Problem #3) (1 + sin(2x) - cos(2x))/(1 + sin(2x) + cos(2x)) = tan(x)
Hint: use the identities cos(2x) = 1 - 2sin²(x) = 2cos²(x) - 1 and sin(2x) = 2sin(x)cos(x) to express the left-hand side in terms of sin(x) and cos(x), then factorize the numerator and denominator.
(Problem #4) sin(2x) + (1/sin(2x)) = 5/2; for 0 ? x <2?
This is an equation you have to solve, not an identity. Start by treating it as a quadratic equation in sin(2x). The quadratic factorizes easily.
(True or false)car traveling 20 meters per hour east of the mountain pass is example of velocity
Answers
Answer:
It's true
Step-by-step explanation:
I need help! 25 brainly points!
Answers
The surface areas for each figures are:
220 ft² 410 cm²596 cm²360 cm²Surface area of cylinders include: 132π mm²22π ft²396π square inches.How to calculate surface areas?1. The surface area of the cuboid is:
Top and bottom: 2(10 ft x 4 ft) = 80 ft²
Front and back: 2(10 ft x 5 ft) = 100 ft²
Sides: 2(4 ft x 5 ft) = 40 ft²
Total surface area = 80 + 100 + 40 = 220 ft²
2. The surface area of the cuboid is:
Top and bottom: 2(18 cm x 5 cm) = 180 cm²
Front and back: 2(18 cm x 5 cm) = 180 cm²
Sides: 2(5 cm x 5 cm) = 50 cm²
Total surface area = 180 + 180 + 50 = 410 cm²
3. The surface area of the prism is:
Top and bottom: 2(5 cm x 14 cm) = 140 cm²
Front and back: 2(5 cm x 12 cm) = 120 cm²
Sides: 2(12 cm x 14 cm) = 336 cm²
Total surface area = 140 + 120 + 336 = 596 cm²
4. The surface area of the stacked cuboids is:
Top and bottom of first cuboid: 2(6 cm x 7 cm) = 84 cm²
Front and back of first cuboid: 2(6 cm x 2 cm) = 12 cm²
Sides of first cuboid: 2(7 cm x 2 cm) = 28 cm²
Front and back of second cuboid: 2(7 cm x 2 cm) = 28 cm²
Sides of second cuboid: 2(2 cm x 4 cm) = 8 cm²
Front and back of third cuboid: 2(2 cm x 10 cm) = 40 cm²
Sides of third cuboid: 2(10 cm x 8 cm) = 160 cm²
Total surface area = 84 + 12 + 28 + 28 + 8 + 40 + 160 = 360 cm²
5. The surface area of the cylinder is:
Top and bottom: 2π(6 mm)² = 72π mm²
Side: 2π(6 mm)(5 mm) = 60π mm²
Total surface area = 72π + 60π = 132π mm²
6. The surface area of the cylinder is:
Top and bottom: 2π(1 ft)² = 2π ft²
Side: 2π(1 ft)(10 ft) = 20π ft²
Total surface area = 2π + 20π = 22π ft²
7. The surface area of the cylinder stacked on a cube is:
Top and bottom of cylinder: 2π(5 m)² = 50π m²
Side of cylinder: 2π(5 m)(8 m) = 80π m²
Surface area of cube: 6(10 m x 13 m) = 780 m²
Total surface area = 50π + 80π + 780 = (130π + 780) m²
8. The surface area of the cylinder is:
Top and bottom: 2π(9 in)² = 162π in²
Side: 2π(9 in)(4 in) = 72π in²
Therefore, the total surface area of the cylinder is:
2(162π in²) + 72π in² = 396π in²
So the surface area of the cylinder is 396π square inches.
Find out more on surface area here: https://brainly.com/question/16519513
#SPJ1
Image transcribed:
Find the surface area of each figure.
10 ft
18 cm
5 cm
4 ft
5 ft
3.
4.
6 cm
7 cm
2 cm
5 cm
12 cm
14 cm
4 cm
10 cm
8 cm
Find the surface area of each cylinder. Leave your answer in terms of π.
5.
6 mm
6.
1 ft
5 mm
10 ft
7.
5 m
8.
4 in.
8 m
10 m
9 in.
13 m
11 m
247
Journal and Practice Workbook
Geometry
SHARE 300 USING 2:3:5
Answers
If we divide 300 into parts using the ratio 2:3:5, we get:
2 parts = 2/10 of the total ratio = 2/10 x 300 = 60
3 parts = 3/10 of the total ratio = 3/10 x 300 = 90
5 parts = 5/10 of the total ratio = 5/10 x 300 = 150
Therefore, 300 divided in the ratio 2:3:5 would result in three parts of 60, 90, and 150.
I hope I helped!
~~~Harsha~~~
a 12-foot piece of string is cut into two pieces so that the longer piece is 3 feet longer than twice the shorter piece. if the shorter piece is x feet long, find the lengths of both pieces.
Answers
Answer:
3 ft and 9 ft
Step-by-step explanation:
Let g(x) be the indicated transformation of f(x) = −|3x| − 4. Stretch the graph of f(x) = −|3x| − 4 vertically by a factor of 3 and reflect it across the x-axis. Identify the rule and graph of g(x).
Answers
The final rule for g(x) is g(x) = 3|3x| + 12.
To stretch the graph of f(x) = −|3x| − 4 vertically by a factor of 3, we multiply the function by 3. This will result in a vertical stretching of the graph.
So, the rule for g(x) is g(x) = 3f(x).
Now, let's find the expression for g(x) using the given function f(x) = −|3x| − 4:
g(x) = 3f(x)
g(x) = 3(-|3x| - 4)
g(x) = -3|3x| - 12
This is the expression for g(x), which represents the transformed graph.
To reflect the graph of g(x) across the x-axis, we change the sign of the function. This means that the negative sign in front of the absolute value will become positive, and the positive sign in front of the constant term will become negative.
Therefore, the final rule for g(x) is g(x) = 3|3x| + 12.
Now, let's consider the graph of g(x). The graph will have the same shape as f(x), but it will be stretched vertically by a factor of 3 and reflected across the x-axis.
The original graph of f(x) = −|3x| − 4 is a V-shaped graph that opens downward and passes through the point (0, -4). The transformed graph of g(x) will have a steeper V-shape, opening downward, and passing through the point (0, 12) instead of (0, -4).
For more such questions on final rule visit:
https://brainly.com/question/30396691
#SPJ8
HELPPPP PLEASEEEEEEEEE
Answers
Answer: 44
Step-by-step explanation:
The interior and exterior in these type of problems equal 180. 180 – 136 = 44
find all the zeros of polynomial functionsf(x)=24x^4-2x^3-35x^2-4x+5
Answers
To find the zeros of a polynomial, we can graph the function given as follows:
From the graph, we have that the roots are:
• (-1, 0)
,• (-1/2, 0)
,• (1/3, 0) (We can express 1/3 as a periodic decimal as 0.33333...)
,• (5/4, 0) (5/4 is equivalent to 1.25).
We have that the Fundamental Theorem of Algebra tells us that this fourth-degree polynomial must have 4 roots (including multiple and complex roots).
In this case, we have four different roots.
They are NOT multiple (repeated roots) or complex roots. We have four rational roots, and we can verify them from the graph. The roots are those ones where the function passes through the x-axis and when y = 0.
Therefore, these roots are x = -1, x = -1/2, x = 1/3, x = 5/4.
We can check this result if we substitute each of these values into the polynomial function, f(x):
\(f\mleft(x\mright)=24x^4-2x^3-35x^2-4x+5\)\(f(-1)=24\cdot(-1)^4-2\cdot(-1)^3-35\cdot(-1)^2-4\cdot(-1)+5=24+2-35+4+5=0_{}\)And we can do the same for the rest of the roots: x = -1/2, x = 1/3, x = 5/4, we will obtain zero for the function, f(x).
What equation has a negative slope and a y-intercept of zero?
Answers
Answer:
An equation that has a negative slope and a y intercept if the slope is negative and the intersection point is negative.
Step-by-step explanation: Example Y=-3x-4(negative
Posotive=Y=3x+4
Let U= {1, 7, 6, 14, 11, 13, 4, 18}
A = {1, 4, 18}
C = {7, 6, 14, 11, 13}
Find A U C'.
Answers
The elements 1, 4, and 18 belong to the set A U C' represents the union of set A and the complement of set C.
To find the union of set A and the complement of set C (denoted as C'), you need to combine the elements that belong to either A or the complement of C.
First, let's find the complement of set C:
C' = U - C = {1, 7, 6, 14, 11, 13, 4, 18} - {7, 6, 14, 11, 13} = {1, 4, 18}
The complement of set C (C') consists of all the elements in the universal set U that are not present in set C.
Now, let's find the union of set A and C':
A U C' = {1, 4, 18} U {1, 4, 18} = {1, 4, 18}
The union of set A and C' consists of all the elements that belong to either set A or the complement of set C.
A U C' = {1, 4, 18}.
For similar questions on elements
https://brainly.com/question/25916838
#SPJ8
Please help it’s URGENT!
Answers
The least common denominator needed to solve the equation is given as follows:
D. x(x - 3).
How to obtain the least common denominator?The equation in this problem is given as follows:
1/x + 2/(x - 3) = 5.
The denominators of each expression are given as follows:
x.x - 3.x and x - 3 are not factors of each other, hence we multiply them and the least common denominator needed to solve the equation is given as follows:
D. x(x - 3).
More can be learned about least common denominator at https://brainly.com/question/19249494
#SPJ1
PLEASE HELP ME QUICK!!!
Answers
Answer:
Option D. \(g(x)=5(0.8)^{x}+2\)
Step-by-step explanation:
Main concepts
Concept 1: identifying horizontal asymptote
Concept 2: assuring decreasing exponential function
Concept 1. identifying horizontal asymptote
Any exponential function of the form \(y=a*b^x\) has a horizontal asymptote on the x-axis. A constant (positive or negative) added to the end of the exponential expression will shift the graph of the exponential function up (if positive) or down (if negative) the number of units equal to the magnitude of the number. Since the original function f(x) has a "+2" at the end, it has been shifted up 2 units. Thus, we can eliminate answers A and C from feasible answers since they each shift the exponential function up 3 units, not 2.
Concept 2. assuring decreasing exponential function
Exponential functions of the form \(y=a*b^x\) increase or decrease based on the value of "b".
If "b" is between 0 and 1 (a "small" number), the function will decrease.If "b" is larger than 1 (a "big" number), the function will increase.Observe that the graph of the function f(x) is decreasing, and the value of b=0.5.
To ensure that g(x) also decreases, the b-value must be between 0 and 1, which eliminates option B.
Option D is the correct answer because the value of "b" is between 0 and 1 (making the graph of the function a decreasing exponential), and the number added at the end is "+2", causing the horizontal asymptote to be at a height of positive 2.
Can someone please help me I will mark u brilliant
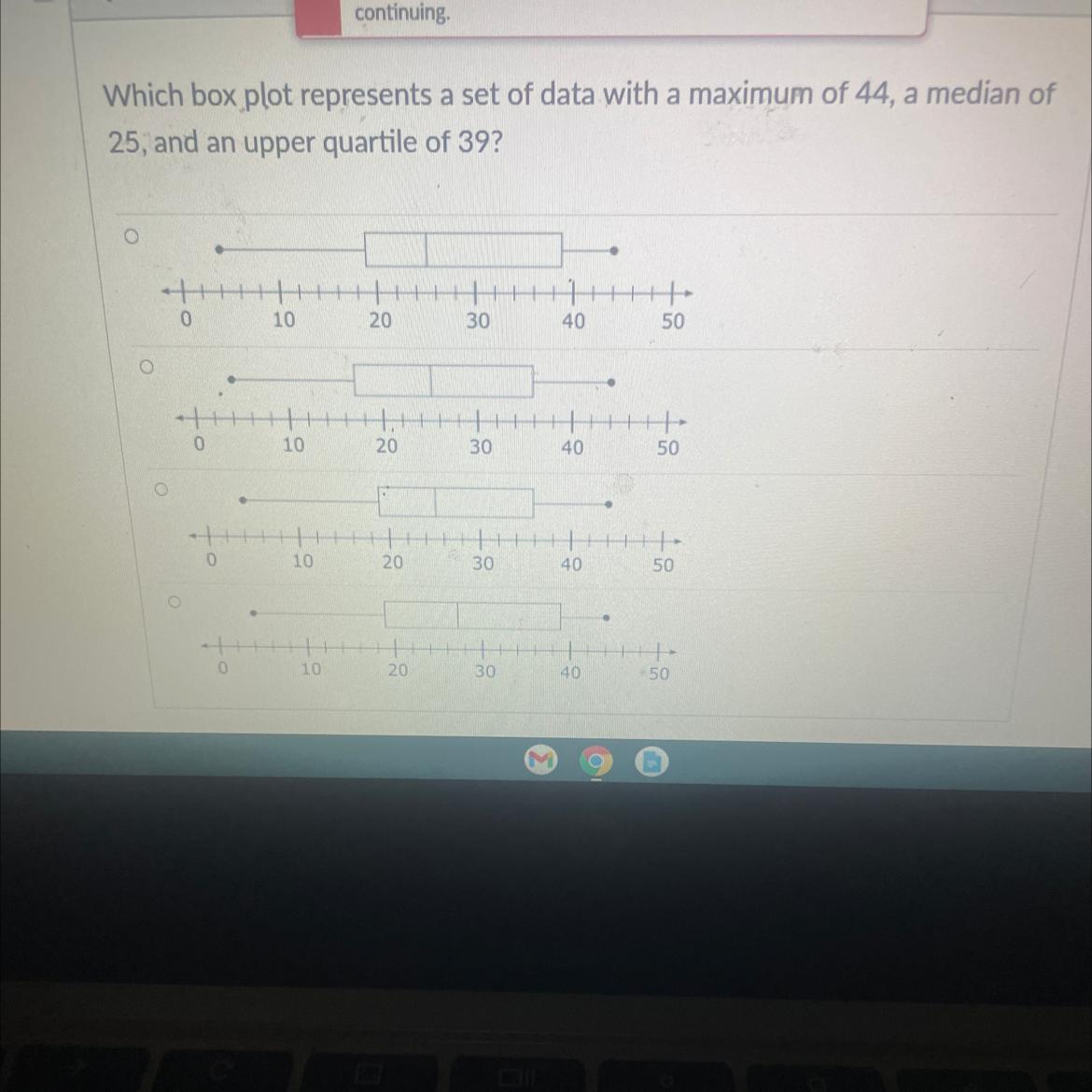
Answers
Answer:
the first one
Step-by-step explanation:
The problem says that the plot must have a maximum of 44, which means the most right dot must be on the 44 mark. All the graphs fit this requirement (the dashes are in increments of 2) The problem says that it must have an upper quartile of 39, which means the line closest to the maximum dot must be on the 39 mark. Graphs 2 and 3 do not meet this requirement, so they are eliminated. The last requirement is the median of 25. The median is represented by the middle line in the middle of the boxes. Graph 4 does not fit this requirement, so it is eliminated. Thus, only the first graph follows all 3 requirements.
Why is occurring when work is being done 
Answers
Select the expression that is equivalent to 2x3+11x2−21xx2+3x for x ≠ −3 or 0 .
Answers
Answer:
\(\frac{(2x-3)(x+7)}{x+3}\)
Step-by-step explanation:
Given
\(\frac{2x^3+11x^2-21x}{x^2+3x}\)
Required
Select equivalent expression
\(\frac{2x^3+11x^2-21x}{x^2+3x}\)
Factorize the numerator and denominator
\(\frac{x(2x^2+11x-21)}{x(x+3)}\)
Divide by x/x
\(\frac{2x^2+11x-21}{x+3}\)
Expand the numerator
\(\frac{2x^2+14x-3x-21}{x+3}\)
Factorize the numerator
\(\frac{2x(x+7)-3(x+7)}{x+3}\)
\(\frac{(2x-3)(x+7)}{x+3}\)
Hence, the equivalent expression is:
\(\frac{(2x-3)(x+7)}{x+3}\)
Keegan is determining whether the triangle with vertices L(-1, 3), M(5, 5) and N(7, -1) is a right triangle. Keegan finds the slopes as shown and concludes that the triangle is not a right triangle because the product is not -1. What is his error and what should he do to correct it?
(added an image)
will mark brainiliest
Answers
Keegan's error is assuming that the product of the slopes of any two sides of a triangle should be -1 for the triangle to be a right triangle.
To determine if the triangle LMN is a right triangle, Keegan should instead calculate the lengths of the three sides of the triangle and check if they satisfy the Pythagorean theorem.
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the lengths of the other two sides.
To correct his approach, Keegan should calculate the lengths of sides LM, MN, and NL using the coordinates of the vertices and then check if the Pythagorean theorem holds true.
If the squared length of one side is equal to the sum of the squares of the other two sides, then the triangle LMN is a right triangle.
To learn more on Triangles click:
https://brainly.com/question/2773823
#SPJ1
A piece of plywood 24 inches wide is cut into strips 2 ½ inches wide. How many strips of this width can be cut? Strips.
Answers
Answer:
9 Strips
Step-by-step explanation:
24 / 2.5 = 24 ÷ \(\frac{5}{2}\) = \(\frac{24}{1}\) x \(\frac{2}{5}\) = \(\frac{48}{5}\) = 9.6
This is rounded down to 9.
f(x) = x + 1, g(x) = 7x + 8 find (fog)(x)
Answers
Answer:
7x + 9
Step-by-step explanation:
f(x) = x + 1
g(x) = 7x + 8
therefore, (fog)(x) = f(g(x))
f(g(x)) = (7x + 8) + 1
= 7x + 9
Pollsters are concerned about declining levels of cooperation among persons contacted in surveys. A pollster contacts 99 people in the 18-21 age bracket and finds that 84 of them respond and 15 refuse to respond. When 276 people in the 22-29 age bracket are contacted, 257 respond and 19 refuse to respond. Assume that 1 of the 375 people is randomly selected. Find the probability of getting someone in the 18-21 age bracket or someone who agreed to respond.
Answers
Answer:
The probability of getting someone in the 18-21 age bracket or someone who agreed to respond \(= 0.365\)
Step-by-step explanation:
The counts are as follows
Age Group No of people contacted No of refusals Total
18-21 88 8 96
22-29 240 42 282
Total 328 50 378
The probability of getting some one in the age bracket of 18-21 or some one who refused to respond is
\(= \frac{96}{378} + \frac{50}{378} - \frac{8}{378} \\= \frac{96+50-8}{378} \\= \frac{138}{378} \\= 0.365\)
there are 7 people to be seated in a row. answer the following.A. Find The Number Of Combinations If There Are No Restrictions On The Seating Arrangements. B. There Are Three Friends That Must Sit Together. Find The Number Of Combinations In Which The Three Friends Are Next To Each Other. C. Suppose That An Usher Randomly Assigns The Seats To The 7
Answers
A) The Number of Combinations if there are no restrictions on the seating arrangements are 5040 ways.
B) There are three friends That must sit together
in 36 ways.
C) Three friends are next To each other in 144 different ways.
Total number of people = 7 and seated in a row.
Combination is arrangement of objects in a particular order. The formula of combination is
ⁿCₓ = n!/(n-x)! x!
n --> total number of objects
we have to determine how many ways can 7 be seated in a row.
A) if there are no restrictions on seating arrangement, The number of possible ways = n!
Here, n! = 7!
= 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040 ways.
Therefore, there are 5040 ways that the people can be seated when there is no restriction on the seating arrangement.
b) There are three friends that must sit Together. The three persons can be arranged in 3!
The possible number of ways = 3! × 3! × 1
= 3× 2×1 ×3×2×1
= 36
C) If there are three friends must sit next to one another. There are total seven persons . Three persons sit next to one another. The possible number of ways = 3! × 4!
= ( 3 × 2 × 1) × (4 × 3 × 2 × 1)
= 6 × 24
= 144 ways
Therefore, if there are 3 sit next to one another, there are 144 ways of seating arrangement.
To learn more about Combination, refer:
https://brainly.com/question/28065038
#SPJ4
solve the equation x-23=18
Answers
Answer:
x = 41
Step-by-step explanation:
x-23=18
Add 23 to each side
x-23+23=18+23
x =41
three sides of triangle is x cm y cm z cm its perimeter and semi perimeter
Answers
Answer:
Step-by-step explanation:
Perimeter:
\(P=(x+y+z) \ cm\)
Semi-perimeter:
\(SP=\frac{1}{2} (x+y+z) \ cm\)
Simplify by reducing the index of th
21/ 15
√X
Answers
Answer:
simplify the reducing the index of the
21/15√x
Step-by-step explanation:
Answer:
26
Step-by-step explanation:
How many 1/4 are in 3
Answers
Answer:
3 ithinks so it lol haha
Answer: 12
Step-by-step explanation:
The are 4 1/4 in 1
3x4=12
Find the LCM of A= 3^2 x 5^4 x 7 and B= 3^4 x 5^3 x 7 x11
Answers
The LCM of A = 3² × 5⁴ × 7 and B = 3⁴ × 5³ × 7 × 11 is 3898125 using Prime factorization.
Given are two numbers which are showed in the prime factorized form.
A = 3² × 5⁴ × 7
B = 3⁴ × 5³ × 7 × 11
Prime factorization is the factorization of a number in terms of prime numbers.
In order to find the LCM of these two numbers, we have to first match the common primes and write down vertically when possible and then bring down the primes in each column.
A = 3² × 5³ × 5 × 7
B = 3² × 3² × 5³ × 7 × 11
Bring down the primes in each column.
LCM = 3² × 3² × 5³ × 5 × 7 × 11
= 3898125
Hence the LCM is 3898125.
Learn more about LCM here :
https://brainly.com/question/6756370
#SPJ1
Use the distributive property to remove the parentheses (x+12)8
Answers
Answer:
Using distributive property to solve \((x+12)8\) we get \(\mathbf{8x+96}\)
Step-by-step explanation:
We need to used distributive property to solve (x+12)8
The distributive property of multiplication or addition states that: \(a(b+c)=ab+ac\)
Using the property:
\((x+12)8\\=8x+8*12\\=8x+96\)
So, using distributive property to solve \((x+12)8\) we get \(\mathbf{8x+96}\)
Find the total amount due on a loan of $5,000 for 8 years at 10% simple interest.
$4,000
$5,500
$9,000
$9,500
$5,400
Answers
4√5x - √80x+√45x
Help please
Answers
Answer:
Step-by-step explanation:
Remark
√80 = √(16 * 5) = 4√5 I will put the - sign in when I gather terms
√45 = √(9 * 5) = 3√5
Expression
4√5x - √80x+√45x
Solution
4√5x - 4√5x + 3√5x
The first two terms cancel out
3√5x is all that is left
Answer: 3√5x
You want to restrict the domain of the function shown in the graph below to make it one-to-one so that it will have an inverse. What are the largest domains, in interval notation you could use
Answers
Answer:
(-∞, -3] or [-3, ∞)
Step-by-step explanation:
You want the largest domain interval(s) on which the function shown in the graph could be one-to-one.
One-to-oneA one-to-one function must pass the horizontal line test. That is, no horizontal line can intersect its graph in more than one place.
ApplicationFor that to be true of the given function, the interval on which it is defined cannot include values on both sides of x=-3, where the graph has a minimum. That is, the domain must be either x ≤ -3, or x ≥ -3, (or some subset of either of these).
The largest intervals on which the function has an inverse are ...
(-∞, -3] or [-3, ∞)
<95141404393>
To make the given function one-to-one and have an inverse, we can restrict its domain to (-∞, a) or (a, ∞), where 'a' is the x-coordinate of the highest or lowest point on the graph.
Explanation:To make the given function one-to-one and have an inverse, we need to restrict its domain. The largest domains, in interval notation, that can be used are: (-∞, a) or (a, ∞) where 'a' is the x-coordinate of the highest or the lowest point on the graph, depending on the function type.
If the graph has a highest point, the domain is restricted to (a, ∞), where 'a' is the x-coordinate of the highest point. If the graph has a lowest point, the domain is restricted to (-∞, a), where 'a' is the x-coordinate of the lowest point.
For example, if the graph has a highest point at (3, 5), the domain would be restricted to (3, ∞) to make the function one-to-one and have an inverse.
Learn more about Restricting Domain here:https://brainly.com/question/32491116
#SPJ2
2
h(x)=
8
1
x
3
−x
2
h, left parenthesis, x, right parenthesis, equals, start fraction, 1, divided by, 8, end fraction, x, cubed, minus, x, squared
Over which interval does
h
hh have a positive average rate of change?
Answers
At 6 ≤ x ≤ 8, The function has a positive rate of change.
The correct option is D.
What is a slope?In mathematics, a line's slope, also known as its gradient, is a numerical representation of the line's steepness and direction
If a line passes through two points (x₁ ,y₁) and (x₂, y₂) ,
then the equation of line is
y - y₁ = (y₂- y₁) / (x₂ - x₁) x (x - x₁)
To find the slope;
m = (y₂- y₁) / (x₂ - x₁)
Given:
A quadratic function,
h(x) = (1/8)x³ - x².
h(0) = 0
h(2) = -3
h(6) = -9
h(8) = 0
The average rate of change of the function at 0 ≤ x ≤ 8,
= h(8) - h(0)/(8 - 0)
= 0
The average rate of change at 0 ≤ x ≤ 6,
= h(6) - h(0)/(6 - 0)
= -9/6
The average rate of change of the function at 0 ≤ x ≤ 2,
= h(2) - h(0)/(2 - 0)
= -3/2
The average rate of change of the function at 6 ≤ x ≤ 8,
= h(8) - h(6)/(8 - 6)
= (0 + 9)/(2)
= 9/2
Therefore, the function has a positive rate of change at 6 ≤ x ≤ 8.
To learn more about the slope;
brainly.com/question/3605446
#SPJ1