The class took a math quiz, and the scores were {9, 8, 7, 9, 6, 9, 10, 8, 5, 9, 7, 6, 9, 9, 2, 8, 10, 7}.
Which score(s) were outliers?
Answers
Answer:
2,10,5,6
Step-by-step explanation:
What are outliers?
Outliers are numbers that are not often used and rarely used. They are least showed. The most number used is called the mode, or average. In this case, the mode is mostly 9. Since numbers like 2,10,5, and 6 are numbers that don't show often, they are outliers. Hope this helped
Answer:
2
Step-by-step explanation:
An outlier is the number that brings that mean/average way down or way up. The outlier in this case is 2 b/c it brought down the mean/average.
Related Questions
find the future value of $750 deposited each month at 3.25% for 15 years
Answers
Answer:
P=1538.461
Step-by-step explanation:
do it by the formula of
I=PRT, I=750 R=3.25% T=15
if school starts at 8:15 am and ends at 3:31 pm when how long is the school day
Answers
Answer:
7hours and 16 minutes
Step-by-step explanation:
8:15-9:15 is one hour. 9:15-10:15 is two hours. 10:15-11:15 is three hours.11:15-12:15 is four hours. 12:15-1:15 is five hours. 1:15-2:15 is six hours. 2:15-3:15 is seven hours. 3:15-3:31 is 16 minutes.
3.12 If h(t)= [u(t-1)- u(t - 4)] and x(t) = t[u(t)- u(t-2)], obtain graphically the response y(t). For what value of t does y(t) reach its maximum value?
Answers
The response y(t) graphically, we can first plot the individual functions h(t) and x(t) on a graph, and then determine their convolution to obtain y(t). Let's go step by step:
Plotting h(t):
The function h(t) is defined as h(t) = [u(t-1) - u(t-4)].
The unit step function u(t-a) is 0 for t < a and 1 for t ≥ a. Based on this, we can plot h(t) as follows:
For t < 1, h(t) = [0 - 0] = 0
For 1 ≤ t < 4, h(t) = [1 - 0] = 1
For t ≥ 4, h(t) = [1 - 1] = 0
So, h(t) is 0 for t < 1 and t ≥ 4, and it jumps up to 1 between t = 1 and t = 4. Plotting h(t) on a graph will show a step function with a jump from 0 to 1 at t = 1.
Plotting x(t):
The function x(t) is defined as x(t) = t[u(t) - u(t-2)].
For t < 0, both u(t) and u(t-2) are 0, so x(t) = t(0 - 0) = 0.
For 0 ≤ t < 2, u(t) = 1 and u(t-2) = 0, so x(t) = t(1 - 0) = t.
For t ≥ 2, both u(t) and u(t-2) are 1, so x(t) = t(1 - 1) = 0.
So, x(t) is 0 for t < 0 and t ≥ 2, and it increases linearly from 0 to t for 0 ≤ t < 2. Plotting x(t) on a graph will show a line segment starting from the origin and increasing linearly with a slope of 1 until t = 2, after which it remains at 0.
Obtaining y(t):
To obtain y(t), we need to convolve h(t) and x(t). Convolution is an operation that involves integrating the product of two functions over their overlapping ranges.
In this case, the convolution integral can be simplified because h(t) is only non-zero between t = 1 and t = 4, and x(t) is only non-zero between t = 0 and t = 2.
The convolution y(t) = h(t) * x(t) can be written as:
y(t) = ∫[1,4] h(τ) x(t - τ) dτ
For t < 1 or t > 4, y(t) will be 0 because there is no overlap between h(t) and x(t).
For 1 ≤ t < 2, the convolution integral simplifies to:
y(t) = ∫[1,t+1] 1(0) dτ = 0
For 2 ≤ t < 4, the convolution integral simplifies to:
y(t) = ∫[t-2,2] 1(t - τ) dτ = ∫[t-2,2] (t - τ) dτ
Evaluating this integral, we get:
\(y(t) = 2t - t^2 - (t - 2)^2 / 2,\) for 2 ≤ t < 4
For t ≥ 4, y(t) will be 0 again.
Maximum value of y(t):
To find the value of t at which y(t) reaches its maximum value, we need to examine the expression for y(t) within the valid range 2 ≤ t < 4. We can graphically determine the maximum by plotting y(t) within this range and identifying the peak.
Plotting y(t) within the range 2 ≤ t < 4 will give you a curve that reaches a maximum at a certain value of t. By visually inspecting the graph, you can determine the specific value of t at which y(t) reaches its maximum.
Learn more about function here:
https://brainly.com/question/11624077
#SPJ11
what is the difference between relative frequency and cumlative relative frequency
Answers
The difference between relative frequency and cumulative relative frequency is that relative frequency is the ratio of the frequency of a particular value in a dataset to the total number of values, expressed as a percentage. Cumulative relative frequency is the sum of all relative frequencies up to a certain point in the data set.
For example, if a data set has 8 values and 4 are the same, the relative frequency would be 50%. Cumulative relative frequency would be 50% at this point since it is the sum of all relative frequencies up to this point in the data set. If there were another 4 of the same values after this point, the relative frequency would remain at 50%, but the cumulative relative frequency would increase to 100% since it includes all previous relative frequencies.
To learn more about frequency:
https://brainly.com/question/26146342
#SPJ4
Students arrive at the Administrative Services Office at an average of one every 12 minutes, and their requests take on average 10 minutes to be processed. The service counter is staffed by only one clerk, Judy Gumshoes, who works eight hours per day. Assume Poisson arrivals and exponential service times. Required: (a) What percentage of time is Judy idle? (Round your answer to 2 decimal places. Omit the "%" sign in your response.) (b) How much time, on average, does a student spend waiting in line? (Round your answer to the nearest whole number.) (c) How long is the (waiting) line on average? (Round your answer to 2 decimal places.) (d) What is the probability that an arriving student (just before entering the Administrative Services Office) will find at least one other student waiting in line? (Round your answer to 3 decimal places.)
Answers
The probability that an arriving student will find at least one other student waiting in line is approximately 0.167.
To solve this problem, we'll use the M/M/1 queueing model with Poisson arrivals and exponential service times. Let's calculate the required values: (a) Percentage of time Judy is idle: The utilization of the system (ρ) is the ratio of the average service time to the average interarrival time. In this case, the average service time is 10 minutes, and the average interarrival time is 12 minutes. Utilization (ρ) = Average service time / Average interarrival time = 10 / 12 = 5/6 ≈ 0.8333
The percentage of time Judy is idle is given by (1 - ρ) multiplied by 100: Idle percentage = (1 - 0.8333) * 100 ≈ 16.67%. Therefore, Judy is idle approximately 16.67% of the time. (b) Average waiting time for a student:
The average waiting time in a queue (Wq) can be calculated using Little's Law: Wq = Lq / λ, where Lq is the average number of customers in the queue and λ is the arrival rate. In this case, λ (arrival rate) = 1 customer per 12 minutes, and Lq can be calculated using the queuing formula: Lq = ρ^2 / (1 - ρ). Plugging in the values: Lq = (5/6)^2 / (1 - 5/6) = 25/6 ≈ 4.17 customers Wq = Lq / λ = 4.17 / (1/12) = 50 minutes. Therefore, on average, a student spends approximately 50 minutes waiting in line.
(c) Average length of the line: The average number of customers in the system (L) can be calculated using Little's Law: L = λ * W, where W is the average time a customer spends in the system. In this case, λ (arrival rate) = 1 customer per 12 minutes, and W can be calculated as W = Wq + 1/μ, where μ is the service rate (1/10 customers per minute). Plugging in the values: W = 50 + 1/ (1/10) = 50 + 10 = 60 minutes. L = λ * W = (1/12) * 60 = 5 customers. Therefore, on average, the line consists of approximately 5 customers.
(d) Probability of finding at least one student waiting in line: The probability that an arriving student finds at least one other student waiting in line is equal to the probability that the system is not empty. The probability that the system is not empty (P0) can be calculated using the formula: P0 = 1 - ρ, where ρ is the utilization. Plugging in the values:
P0 = 1 - 0.8333 ≈ 0.1667. Therefore, the probability that an arriving student will find at least one other student waiting in line is approximately 0.167.
To learn more about Probability, click here: brainly.com/question/16988487
#SPJ11
What is 9 - 2 to the power 2 to the power of 4 / 4 + 3 to the power of 5
Answers
Answer:
what is 3x to the power of 2 ×4x to the power of 5
f(x) = x² +4
(a) Find the interval on which fis increasing. (Enter your answer using interval notation.)
Find the interval on which fis decreasing. (Enter your answer using interval notation.)
(b) Find the local maximum and minimum values of f.
local minimum value
local maximum value
Answers
Given the function: f(x) = x² +4The derivative of the function can be found by applying the power rule: f'(x) = 2x(a) To find the intervals where the function is increasing, decreasing or stationary, we need to solve for f'(x) = 0: f'(x) = 2x = 0 ⇒ x = 0At x = 0, the function is stationary. We can then use the first derivative test to determine the intervals where the function is increasing and decreasing.
From the first derivative test: if f'(x) > 0, the function is increasingif f'(x) < 0, the function is decreasingif f'(x) = 0, the function is stationaryThe sign of the derivative of the function depends on the value of x. We can use test values from each interval to determine the sign of the derivative and hence the intervals where the function is increasing or decreasing:The intervals where the function is increasing: (-∞, 0) U (0, ∞)The intervals where the function is decreasing: (0, 0) = {0}.
The interval notation for the intervals where the function is increasing and decreasing:Increasing: (-∞, 0) U (0, ∞)Decreasing: {0}(b) To find the local maximum and minimum values of f, we need to find the critical points of the function. At x = 0, the function is stationary. We can then use the second derivative test to determine whether the stationary point is a maximum, minimum or neither:f'(x) = 2xf''(x) = 2At x = 0, f''(0) = 2 > 0. Therefore, the stationary point is a local minimum. The local minimum value occurs at x = 0. Thus, the local minimum value of f is f(0) = 0² + 4 = 4.There is no local maximum value as the function does not have any other stationary points.
Learn more about power rule:
https://brainly.com/question/29288036
#SPJ11
Hello please solve my question. I don’t understand it. Any links will be reported. Thank you (:
Answers
Rachel earns 9 dollars an hour
h · m = 81
9 · 9 = 81
Have a luvely day!
3x + 2x – x + 2x² =
Please help !!
Answers
Answer:
3 + 2 = 5
add x to 5
5x + 2x to the 2nd power
2 times 2 = 4x = 5 and 4x
5x + 4x
Use the given domain to find the range of each function
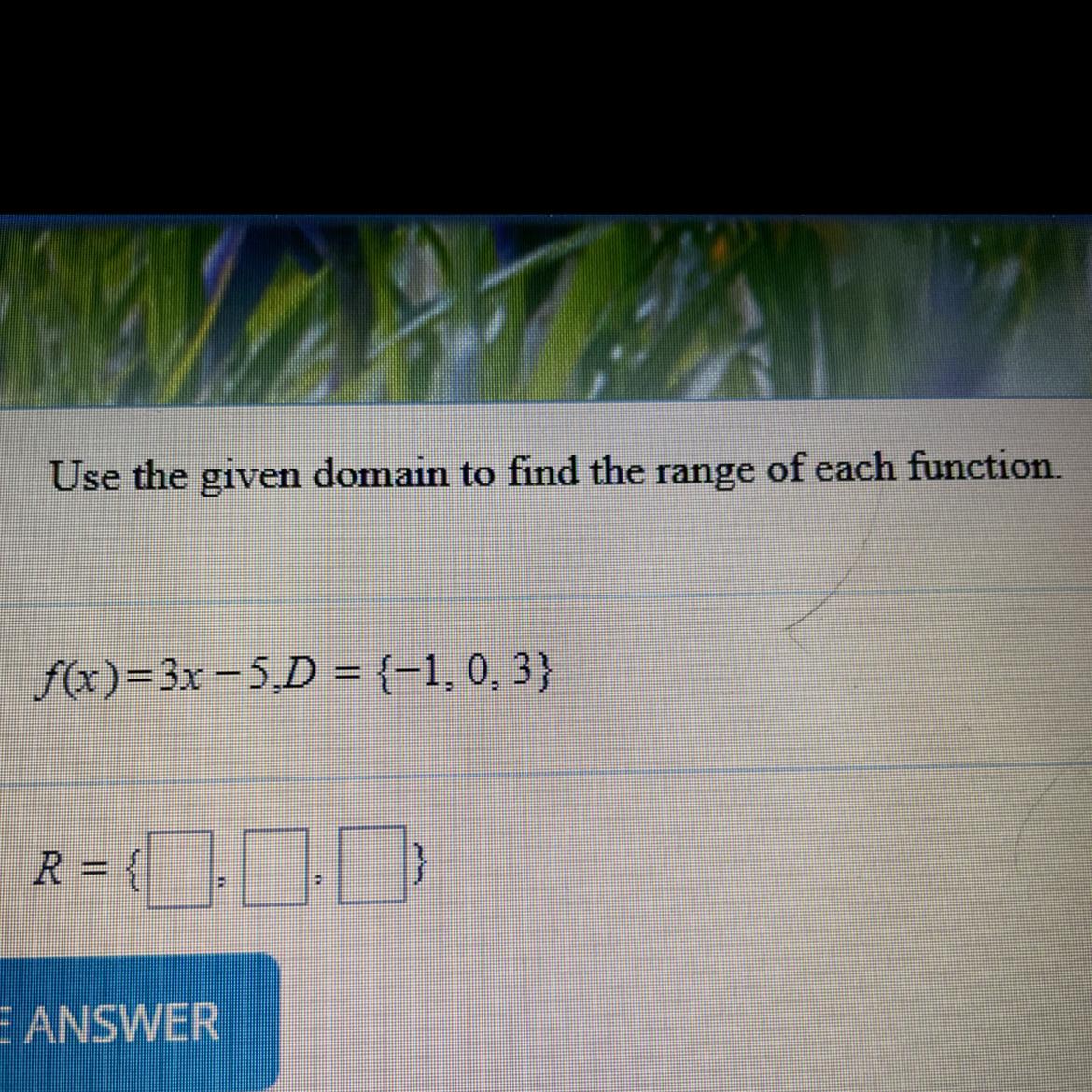
Answers
Answer:-8, -5, 4
Step-by-step explanation:
you just take the number and put them where x is to solve the problem like for -1 example
3(-1)-5
-3 - 5
-9
or 0
3(0) - 5
0 - 5
5
or 3
3(3) - 5
9 - 5
4
Answer:
R = { - 8, - 5, 4 }
Step-by-step explanation:
Substitute the values of x from the domain into f(x) for range
f(- 1) = 3(- 1) - 5 = - 3 - 5 = - 8
f(0) = 3(0) - 5 = 0 - 5 = - 5
f(3) = 3(3) - 5 = 9 - 5 = 4
R = { - 8, - 5, 4 }
Find the area of triangle XYZ if length XY equals 7 and length XZ equals 4.3. You also
know that angle Y equals 79°.
Answers
Answer:
A ≈ 14.8 units²
Step-by-step explanation:
the area (A) of the triangle is calculated as
A = \(\frac{1}{2}\) yz sin Y ( that is 2 sides and the angle between them )
where x is the side opposite ∠ X and z the side opposite ∠ Z
here y = XZ = 4.3 and z = XY = 7 , then
A = \(\frac{1}{2}\) × 4.3 × 7 × sin79°
= 15.05 × sin79°
≈ 14.8 units² ( to 1 decimal place )
how do i solve 3x+2=338
Answers
Answer:
3x+2=338
3x=338-2
3x=336
x=336/3
x=112 is the answer
Step-by-step explanation:
Hope it help ^_^
Answer:
112
Step-by-step explanation:
3x + 2 = 338
-2 = -2 cancel them out
3x= 336
divide by 3
x = 112
The double-reciprocal transformation of the Michaelis-Menten equation, also called the Lineweaver- Burk plot, is given by
1/V_0 = K_m /(V_max[S]) + 1/V_max
To determine Km from a double-reciprocal plot, you would:
A) multiply the reciprocal of the x-axis intercept by -1.
B) multiply the reciprocal of the y-axis intercept by -1.
C) take the reciprocal of the x-axis intercept.
D) take the reciprocal of the y-axis intercept.
E) take the x-axis intercept, where V_0 = 1/2 V_max.
Answers
To determine Km from a double-reciprocal plot, you would choose option (A) which is to multiply the reciprocal of the x-axis intercept by -1.
In the double-reciprocal plot equation, the x-axis intercept is -1/Km, and the y-axis intercept is 1/Vmax. Therefore, if you take the reciprocal of the x-axis intercept, you get -Km, and multiplying it by -1 gives you Km.
This method is preferred because it is more accurate than estimating Km based on the position of the curve on the plot or by taking the x-axis intercept where V0 = 1/2 Vmax, which can be influenced by experimental error.
To learn more about reciprocal here:
https://brainly.com/question/30519664
#SPJ4
Bayesian fidget spinners Nat's company manufactures fidget spinners. The company uses two factories, which we'll call factory 0 and factory 1. Each fidget spinner from factory k is defective with probability Ik (k E {0,1}). Nat knows that factory O produces fewer defective fidget spinners than factory 1 (in other words, qo < qı). She receives n boxes full of fidget spinners, but the boxes aren't labeled (in other words, she doesn't know which box is from which factory). For each box, she starts randomly pulling out fidget spinners until she finds a defective one, and records how many fidget spinners she pulled out (including the defective one). She calls this number Xi for box i, for i = 1,...,n. She wants to estimate the following pieces of information: • Which boxes came from factory 0, and which came from factory 1? She defines a binary random variable for each box zi with the factory label (i.e., zi 0 if box į is from factory 0, and zi = 1 if box i is from factory 1). • How reliable is each factory? In other words, what are qo and qı? Inspired by what she learned about Gaussian mixture models, she sets up the following probability model: zi Bernoulli(7) ak Beta(aksßk) Xi|zi, 90, 91 ~ Geometric(qz:) Nat decides to implement the model above setting the following hyperparameters: T = = 0.3, Po~ Beta(1,5), 01~ - Beta(5,1) (b) Which one of the following explains why Nat chose this value of a: (i) Factory 0 produces more boxes than factory 1 (ii) Factory 0 produces fewer boxes than factory 1 (iii) Factory 0 is better (i.e., it is less likely to produce defective fidget spinners) (iv) Factory 0 is worse (i.e., it is more likely to produce defective fidget spinners) (c) Which one of the following explains why Nat chose these values of a and B? (i) Factory 0 produces more boxes than factory 1 (ii) Factory 0 produces fewer boxes than factory 1 (iii) Factory 0 is better (i.e., it is less likely to produce defective fidget spinners) (iv) Factory 0 is worse (i.e., it is more likely to produce defective fidget spinners)
Answers
(b) (iii) Factory 0 is better than all other factories (i.e., it is less likely to produce defective fidget spinners).
(c) (iii)Factory 0 is better than all other factories (i.e., it is less likely to produce defective fidget spinners).
(b) Nat chose the value of a to be 0.3 because she knows that factory 0 produces fewer defective fidget spinners than factory 1. This means that factory 0 is better, or less likely to produce defective fidget spinners, which is why the value of a is closer to 0 than 1.
(c) Nat chose the values of a and B to be 1 and 5 for factory 0, and 5 and 1 for factory 1, because she knows that factory 0 is better, or less likely to produce defective fidget spinners, than factory 1.
The values of a and B are used to determine the probability of a fidget spinner being defective from each factory, with a lower value of a and a higher value of B indicating a lower probability of a defective fidget spinner.
Therefore, the values of a and B for factory 0 indicate a lower probability of a defective fidget spinner than the values of a and B for factory 1.
To know more about probability click on below link:
https://brainly.com/question/30034780#
#SPJ11
??????????????????????????????
Answers
Answer:
i finished on the other question yw
Step-by-step explanation:
also not sure if you wanted the values for n
edit:
7. n/2 = 16
8. 2n + 4 = 52
9. 2(n + 5) = 17
10. 3n - 12 = 5
Answer:
7. 32
8. 24
9. 3.5
10. 5.6
Step-by-step explanation:
7. write the equation: n/2=16. Cross multiply.
8. write the equation: 52= 4+2n. Move 4 to the other side and subtract from 52: 48= 2n. Divide both sides by 2.
9. write the equation: 2(5+n)=17. Use the distributive property. Move 10 to the other side and subtract from 17: 2n=7. Divide both sides by 2.
10. write the equation 3n-12=5. move -12 over and add to 5: 3n=17. Divide both sides by 3.
brainliest plzzzzzz
1a.We have a weighted coin where the probability of throwing "heads" is p=0.65. Which is more probable:
(i) throwing exactly 15 heads in 20 throws or
(ii) throwing at most 2 heads in 5 throws?
1b. Suppose we flip a fair coin 4 times. For what combination(s) do there exist exactly 3 permutations?
1c. We have a box containing 5 red balls and 3 black balls. Suppose well pull out three balls sequentially, and do not place them back into the box after they’ve been pulled. What is the probability of selecting, in order, a black ball, a red ball, and then another black ball?
Answers
1.a The probability of throwing at most 2 heads in 5 throws is more probable.
1.b A total of 2^4 = 16 outcomes.
1.c The probability of selecting a black ball, a red ball, and then another black ball is 5/56.
1a. Probability of throwing exactly 15 heads in 20 throws
Probability of getting a head is p = 0.65, and the probability of getting tails is q = 1 - 0.65 = 0.35.
Let X be the random variable which counts the number of heads in 20 throws.
Then X follows the binomial distribution B(20, 0.65).P(X = 15) = 20C15 * 0.65^15 * 0.35^5= 0.16
Probability of throwing at most 2 heads in 5 throws
Let Y be the random variable which counts the number of heads in 5 throws.
Then Y follows the binomial distribution B(5, 0.65).P(Y ≤ 2) = P(Y = 0) + P(Y = 1) + P(Y = 2)
= 0.01 + 0.08 + 0.25
= 0.34
Therefore, the probability of throwing at most 2 heads in 5 throws is more probable.
1b. Suppose we flip a fair coin 4 times.
For what combination(s) do there exist exactly 3 permutations?
There are a total of 2^4 = 16 outcomes.
The combinations that exist in exactly 3 permutations are HTTH, HTHT, THHT, THTH, and HHTT.
1c. Probability of selecting a black ball, a red ball, and then another black ball We want to compute the probability of pulling out 3 balls, without replacement, from a box with 5 red balls and 3 black balls.
The total number of ways of pulling out 3 balls is 8C3.
The probability of pulling out a black ball on the first draw is 3/8.
The probability of pulling out a red ball on the second draw is 5/7.
The probability of pulling out another black ball on the third draw is 2/6 = 1/3.
So, the required probability is (3/8) * (5/7) * (1/3) = 5/56.
Therefore, the probability of selecting a black ball, a red ball, and then another black ball is 5/56.
Learn more about probability from this link:
https://brainly.com/question/13604758
#SPJ11
A passenger train traveled 120 miles in the same amount of time it took a freight train to travel 70 miles. The rate of the freight train was 30 miles per hour slower than the rate of the passenger train. Find the rate of the passenger train.
PLEASE HELP ASAP
Answers
Answer: The rate of the passenger train was 72 mph.
Step-by-step explanation:
3x+4(7-2x) =68. Whats the value of x
Answers
Answer:
first we deal with the parentheses.
3x + 28 - 8x = 69
3x - 8x = 41
-5x = 41
x = -8.2
ep-by-step explanation:
Answer:
x = -8
Step-by-step explanation:
Simplify these expressions:
1. 2x + 8x
2. (5y) - 10y
3. W + 14w - 6w
4. 4x - 5x -6
Answers
Answer:
Theyre out of order.
Step-by-step explanation:
T/F: an example of a weight used in the calculation of a weighted index is quantity consumed in a base period.
Answers
False. The quantity consumed in a base period is not an example of a weight used in the calculation of a weighted index.
In the calculation of a weighted index, a weight is a factor used to assign relative importance or significance to different components or categories included in the index. These weights reflect the contribution of each component to the overall index value. The purpose of assigning weights is to ensure that the index accurately reflects the relative importance of the components or categories being measured.
An example of a weight used in a weighted index could be market value, where the weight is determined based on the market capitalization of each component. This means that components with higher market values will have a greater weight in the index calculation, reflecting their larger impact on the overall index value.
On the other hand, the quantity consumed in a base period is not typically used as a weight in a weighted index. Instead, it is often used as a reference point or benchmark for comparison. For example, in a price index, the quantity consumed in a base period is used as a constant quantity against which the current prices are compared to measure price changes.
Therefore, the statement that the quantity consumed in a base period is an example of a weight used in the calculation of a weighted index is false.
To learn more about weight, click here:
brainly.com/question/19053239
#SPJ1
Marcia has two credit cards and would like to consolidate the two balances into one balance on the card with the lower interest rate. The table below shows the information about the two credit cards Marcia currently uses. Card A Card B Amount $1,389. 47 $1,065. 32 APR 16% 12% Monthly Payment $39. 38 $28. 05 After 4 years, approximately how much will Marcia have saved in interest by consolidating the two balances? a. $1,890. 24 b. $133. 92 c. $543. 84 d. $1,346. 40 Please select the best answer from the choices provided. A B C D.
Answers
Marcia will have saved approximately $1,346.40 in interest by consolidating the two balances.To calculate the interest savings by consolidating the two balances,
we need to compare the total interest paid on the two credit cards over a period of 4 years. For Card A: Amount: $1,389.47 APR: 16% Monthly Payment: $39.38 For Card B: Amount: $1,065.32 APR: 12% Monthly Payment: $28.05 To calculate the total interest paid on Card A, we can use the formula: Total Interest = (APR/100) * Principal * Time For Card A: Total Interest = (16/100) * $1,389.47 * 4 years = $888.51 To calculate the total interest paid on Card B: Total Interest = (12/100) * $1,065.32 * 4 years = $511.36 Therefore, the total interest paid on both cards combined without consolidation is $888.51 + $511.36 = $1,399.87. Now let's consider consolidating the two balances into a single balance on the card with the lower interest rate (Card B, 12% APR). Total Consolidated Balance = $1,389.47 + $1,065.32 = $2,454.79 Total Interest on Consolidated Balance = (12/100) * $2,454.79 * 4 years = $1,008.39 By consolidating the two balances, Marcia will save approximately $1,399.87 - $1,008.39 = $391.48 in interest over the 4-year period. However, none of the provided answer choices match this amount. It is possible that there may be an error in the information provided or the calculations involved.
learn more about interest here:
https://brainly.com/question/30393144
#SPJ11
Each student at college has a student ID number consisting for four digits (the first digit is non zero and digits can repeat) followed by four letters A, B, C, D, E, and F (letters cannot repeat). How many different student numbers are possible?
Answers
First, we count the number of ways we can arrange the digits. The first number has 9 possibilities:
\(1\text{ to 9,}\)the other digits have 10 possibilities each:
\(0\text{ to 10.}\)Therefore, the number of ways we can arrange the digits is:
\(9*10*10*10=9*10^3=9000.\)Now, for the letters, the order matters, therefore, we can use the permutation formula:
\(P(6,4)=\frac{6!}{(6-4)!}=360.\)Finally, the total possible number of IDs is:
\(9000*360=3240000.\)Answer: \(\begin{equation*} 3240000. \end{equation*}\)Question attached. Please answer.
Answers
9514 1404 393
Answer:
18 cm²
Step-by-step explanation:
All sides of a rhombus are the same length (as shown by the markings), so one side is 1/4 of the perimeter:
(24 cm)/4 = 6 cm . . . . side length
As with all parallelograms, the area is the product of the side length and the height perpendicular to that side:
A = (6 cm)(3 cm) = 18 cm²
It has an area of 18 cm².
If the force remains constant with magnitude f1 while the object moves a distance d , the final speed of the object is v1 . what is the final speed v2 (in terms of v1 ) if the net force is f2=2f1 and the object moves the same distance d while the force is being applied?
Answers
The final speed v2 is √6 times the initial speed v1, when the net force is 2f1 and the object moves the same distance d while the force is being applied.
We can use the work-energy theorem to solve this problem, which states that the work done on an object by a net force is equal to the change in its kinetic energy.
When the force has magnitude f1 and the object moves a distance d, the work done is:
W = f1 * d
This work changes the kinetic energy of the object from zero to (1/2) * m * v1^2, where m is the mass of the object. Therefore, we have:
f1 * d = (1/2) * m * v1^2
Solving for v1, we get:
v1 = sqrt((2 * f1 * d) / m)
Now, when the net force has magnitude f2 = 2f1 and the object moves the same distance d, the work done is:
W = f2 * d = 2f1 * d
This work changes the kinetic energy of the object from (1/2) * m * v1^2 to (1/2) * m * v2^2, where v2 is the final speed of the object. Therefore, we have:
2f1 * d = (1/2) * m * (v2^2 - v1^2)
Solving for v2, we get:
v2 = sqrt(v1^2 + (4 * f1 * d) / m)
Substituting the expression for v1, we get:
v2 = sqrt((4 * f1 * d) / m + (2 * f1 * d) / m)
Simplifying, we get:
v2 = sqrt(6) * v1
Therefore, the final speed v2 is sqrt(6) times the initial speed v1.
To know more about speed:
https://brainly.com/question/7359669
#SPJ4
Suppose triangle ABC will be dilated using the rule D Subscript Q, two-thirds.
Point Q is the center of dilation. Triangle A B C is 6 units away from point Q. The length of A B is 3, the length of B C is 7, and the length of A C is 8.
What will be the distance from the center of dilation, Q, to the image of vertex A?
2 units
3 units
4 units
6 units
Answers
The distance from the center of dilation, Q, to the image of vertex A will be 4 units.
According to the given rule of dilation, D subscript Q, two-thirds, the triangle ABC will be dilated with a scale factor of two-thirds centered at point Q.
Since point Q is the center of dilation and the distance from triangle ABC to point Q is 6 units, the image of vertex A will be 2/3 times the distance from A to Q. Therefore, the distance from A' (image of A) to Q will be (2/3) x 6 = 4 units.
By applying the scale factor to the distances, we can determine that the length of A'B' is (2/3) x 3 = 2 units, the length of B'C' is (2/3) x 7 = 14/3 units, and the length of A'C' is (2/3) x 8 = 16/3 units.
Thus, the distance from the center of dilation, Q, to the image of vertex A is 4 units.
For more such answers on the Center of dilation
https://brainly.com/question/13173812
#SPJ8
factorisation
\( {x}^{3} - x\)
Answers
Step-by-step explanation:
x³-x
by taking out common term, we get
x(x²-1)
Now, by using the formula of a²-b², we get
x(x²-1²)
x(x+1)(x-1)
I hope it helped U
stay safe stay happy
Answer:
\( {x}^{3} - x = x(x + 1)(x - 1)\)
I hope I helped you^_^
is 3x² - 4ab + 2 a polynomial?
Answers
Answer:
Yes it is a polynomial.
Step-by-step explanation:
3x² - 4ab + 2 is quadratic polynomial, since it has the highest power / degree of 2.
Note : -
Types of polynomials :
Linear Polynomial ( degree 1 )Quadratic Polynomial ( degree 2 )Cubic Polynomial ( degree 3 )Quartic Polynomial ( degree 4 )Answer:
\(4394\)
Step-by-step explanation:
the bird is
Three relatively prime integers are the sides of a right triangle. if the smallest leg has length 28. Find the sum of all the possible values of the hypotenuse.
Answers
The sum of all the possible values of the hypotenuse is 128.4.
According to the statement
we have given that the Three relatively prime integers are the sides of a right triangle and the smallest leg has length 28.
And we have to Find the sum of all the possible values of the hypotenuse.
So, For this purpose, we know that the
Let us consider a three relatively prime integers which are 29,31,37.
we choose these numbers because we have given that the
the smallest leg has length 28.
And according to the Pythagoras theorem.
we know that the
(Hypotenuse)^2 = (Perpendicular)^2 + (Base)^2
And let the smallest length be a base.
So , Put the values of the perpendicular in this one by one then
so,
(Hypotenuse)^2 = (Perpendicular)^2 + (Base)^2
Here Put perpendicular = 29 and base = 28.
Then
(Hypotenuse)^2 = (29)^2 + (28)^2
(Hypotenuse)^2 = 1625
(Hypotenuse) = 40.31
And then
(Hypotenuse)^2 = (Perpendicular)^2 + (Base)^2
Here Put perpendicular = 31 and base = 28.
Then
(Hypotenuse)^2 = (31)^2 + (28)^2
(Hypotenuse)^2 = 1745
(Hypotenuse) = 41.77
And then
(Hypotenuse)^2 = (Perpendicular)^2 + (Base)^2
Here Put perpendicular = 37 and base = 28.
Then
(Hypotenuse)^2 = (37)^2 + (28)^2
(Hypotenuse)^2 = 2153
(Hypotenuse) = 46.40
And then
The all possible values of the hypotenuse are 40.31, 41.77, 46.40.
And the sum become is 128.4
So, The sum of all the possible values of the hypotenuse is 128.4.
Learn more about hypotenuse here
https://brainly.com/question/2217700
#SPJ4
In ΔVWX, x = 1.5 cm, � m∠X=26° and � m∠V=71°. Find the length of v, to the nearest 10th of a centimeter.
Answers
The length of side v in the triangle VWX is 3.2 cm
What is an equation?An equation is an expression that shows how two numbers and variables are related using mathematical operations such as addition, subtraction, exponent, division and multiplication.
Sine rule shows the relationship between the sides and angles of a triangle. It is given by:
a/sin(A) = b/sin(B) = c/sin(C)
In triangle VWX, x = 1.5 cm, m∠X=26° and m∠V=71°. Hence:
v/sin(V) = x/sin(X)
substituting:
v/sin(71) = 1.5/sin(26)
v = 3.2 cm
The length of v is 3.2 cm
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
a pencil that is 4 in. long (starting at x=2) and has a density function of rho(x)=5/x oz/in.
Answers
The mass of the pencil is approximately 5.49 ounces.
To find the mass of the pencil, we can integrate the density function over the length of the pencil.
The density function is given by rho(x) = 5/x oz/in.
We want to find the mass of the pencil, so we integrate the density function from x = 2 (the starting point of the pencil) to x = 6 (the endpoint of the pencil).
The integral is ∫[2, 6] (5/x) dx.
Evaluating the integral, we have:
∫[2, 6] (5/x) dx = 5 ln(x) ∣[2, 6] = 5 ln(6) - 5 ln(2) = 5 (ln(6) - ln(2)).
Using the property of logarithms, we can simplify this to:
5 ln(6/2) = 5 ln(3) ≈ 5 (1.098) ≈ 5.49 oz.
The mass of the pencil is approximately 5.49 ounces.
For more such questions on mass
https://brainly.com/question/28916233
#SPJ8