The coordinate grid shows a pentagon. The pentagon is translated 4 unit to the left and 10 units down to create a new pentagon.
A. (x,y) → (x + 4, y – 10)
B. (x,y) → (x - 4, y – 10)
C. (x,y) → (x - 4, y + 10)
D. (x,y) → (x - 10, y - 4)

Answers
Answer:
B
Step-by-step explanation:
4 units to the left is subtracting
10 units down is subtracting too
hope this helps
Related Questions
A derivative is available with premium W(0)=1.34 when its underlying asset has value S(0)=36. This derivative will have expiry values W(1,↑)=0.64 and W(1,↓)=4.55, when the underlying asset has values S(1,↑)=57 and S(1,↓)=26, respectively. A writer sells 100 of these derivative and wants to set up a portfolio which will have zero cash flow, both at the time the derivative is sold and at the time the derivative expires. The portfolio will include 100 derivatives, borrowed or lent cash, and bought or short sold underlying assets. To ensure a zero cash flow, how many underlying assets should the writer have in the portfolio (with positive meaning bought assets and negative meaning short sold assets)? Give your answer to the nearest integer.
Answers
To ensure a zero cash flow in the portfolio, the writer needs to set up a portfolio that offsets the cash flow from selling the derivatives. The writer should have -3 underlying assets in the portfolio (meaning short sold assets)
The cash flow from selling 100 derivatives can be calculated as:
Cash Flow from selling derivatives = 100 * (Premium at time 0 - Expiry value)
Cash Flow from selling derivatives = 100 * (1.34 - 0.64) = 70
To offset this cash flow, the writer needs to include an equal and opposite cash flow from the underlying assets. Let's assume the writer buys ""x"" underlying assets.
Cash Flow from underlying assets = x * (Value at time 0 - Value at time 1)
Cash Flow from underlying assets = x * (36 - 57) = -21x
To make the cash flow from underlying assets equal to the cash flow from selling derivatives, we set up the equation:
-21x = 70
Solving this equation, we find:
x ≈ -3.33
Since the number of underlying assets must be an integer, we round -3.33 to the nearest integer, which is -3.
Therefore, the writer should have -3 underlying assets in the portfolio (meaning short sold assets).
To know more about derivative, click here: brainly.com/question/25324584
#SPJ11
A parabola has a vertex at (0,0). The equation for the directrix of the parabola is x = –4.
In which direction does the parabola open?
up
down
right
left
Answers
The direction does the parabola open is right. Option C
What is the equation of a parabola?
It is important to note that the general equation of a parabola is: y = a(x-h)² + k or x = a(y-k)² +h
where
⇒ (h , k) denotes the vertex.
Also, the standard equation of a regular parabola is y² = 4ax.
From the equation given , we have
The vertex of the parabola is at (0, 0)Directrix of the parabola is x = -4We know that when the vertex of the parabola is (0, 0) and the directrix is x = - a, the parabola will have the form;
y² = 4ax
It is important to note that ;
If the x - axis has a positive value, the parabola shifts to the leftif the x- axis has a negative value, the parabola shift to the rightFrom this, we can see that the parabola would open in the right direction
Thus, the direction does the parabola open is right. Option C
Learn more about a parabola here:
https://brainly.com/question/4061870
#SPJ1
Three apples and four bananas cost $4.85. Three apples and ten bananas cost 8.75. Find the cost of an apple.
Answers
Answer $0.75
Step-by-step explanation:
3a + 4b = 4.85
3a + 10b = 8.75
Both equations have 3a therefore we can isolate 3a in each equation.
Now:
3a = 4.85 - 4b and 3a = 8.75 - 10b
If 3a each equal different values we now set those values equal and solve for b.
4.85 - 4b = 8.75 - 10b
6b = 3.90
6b/6 = 3.90/6
b = 0.65
Now substitute this into the first equation to solve for a.
3a = 4.85 - 4b
3a = 4.85 - 4(0.65)
3a = 4.85 - 2.60
3a = 2.25
3a/3 = 2.25/3
a = 0.75
A non-repeating, non-terminating decimal is classified as?
Answers
Answer:
A non-terminating, non-repeating decimal is a decimal number that continues endlessly, with no group of digits repeating endlessly. Decimals of this type cannot be represented as fractions, and as a result are irrational numbers. Pi is a non-terminating, non-repeating decimal.
A non-repeating, non-terminating decimal is classified as an irrational numbers.
What are decimal numbers?A decimal is a number that consists of a whole and a fractional part.
Given is the following statement - A non-repeating, non-terminating decimal.
A non - repeating and non - terminating decimal means is a decimal number that has no end and has no specific group of digits repeating endlessly. We cannot write such numbers in the form of x/y. Hence, these numbers are called irrational numbers.
Therefore, a non-repeating, non-terminating decimal is classified as an irrational numbers.
To solve more questions on Irrational numbers, visit the link below-
https://brainly.com/question/4031928
#SPJ2
Determine the end behavior of f(x) x^3-2x^2-x+2n
Answers
Here, we want to determine the end behavior of the given polynomial
To do this, we need to know the leading coefficient sign and the degree of the polynomial (if even or odd)
As we can see, the leading coefficient is a positive number while the degree of the polynomial is odd
So, we need to evaluate the behavior of a polynomial with a positive leading coefficient and an odd degree
The correct answer here is that;
\(\begin{gathered} As\text{ x }\Rightarrow-\infty\text{ , f(x) }\Rightarrow-\infty \\ \text{and;} \\ as\text{ x}\Rightarrow+\infty\text{ , f(x) }\Rightarrow+\infty \end{gathered}\)Answer:
B trustttttttt
Step-by-step explanation:
The Acme Corporation believes that the production of its product in its present facilities will assume logistic growth. These facilities limit production to at most 500 units per day. Presently 200 units per day are produced. The production will increase to 250 units per day in one year. What is the anticipated daily production 3 years from now? (Round down.) a) 402 units per day b) 346 units per day c) 385 units per day d) 323 units per day Allowing for roundoff, which of the following is equ
Answers
The anticipated daily production 3 years from now is approximately 385 units per day.
To determine the anticipated daily production 3 years from now, we can use the logistic growth model. The logistic growth model is given by the equation:
P(t) = K / (1 + A * e^(-k*t))
Where:
P(t) is the population (or in this case, daily production) at time t
K is the carrying capacity or the maximum production limit
A is the initial difference between the carrying capacity and the initial production
k is the growth rate
t is the time in years
Given the information:
Initial production (t = 0): 200 units per day
Production after 1 year (t = 1): 250 units per day
Maximum production limit (K): 500 units per day
We can use these values to find the growth rate (k) and the initial difference (A):
A = K - P(0) = 500 - 200 = 300
P(1) = K / (1 + A * e^(-k*1)) = 250
250 = 500 / (1 + 300 * e^(-k))
1 + 300 * e^(-k) = 500 / 250 = 2
300 * e^(-k) = 2 - 1 = 1
e^(-k) = 1/300
-k = ln(1/300)
k ≈ -5.703
Now, we can calculate the anticipated daily production 3 years from now (t = 3):
P(3) = K / (1 + A * e^(-k*3))
P(3) = 500 / (1 + 300 * e^(-5.703 * 3))
P(3) ≈ 385 units per day
Therefore, the anticipated daily production 3 years from now is approximately 385 units per day.
Learn more about production from the given link:
https://brainly.com/question/16755022
#SPJ11
A rod of length L is placed along the X-axis between X=0 and x=L. The linear density (mass/length) rho of the rod varies with the distance x from the origin as rho=a+bx. (a) Find the SI units of a and b. (b) Find the mass of the rod in terms of a,b and L.
Answers
(a) The linear density (mass/length) rho has SI units of kg/m. Since rho = a + bx, the SI units of a must be kg/m and the SI units of b must be kg/m^2.
(b) To find the mass of the rod, we need to integrate the linear density function over the length of the rod:
m = ∫₀ᴸ ρ(x) dx
Substituting in ρ(x) = a + bx:
m = ∫₀ᴸ (a + bx) dx
m = [ax + (1/2)bx²] from 0 to L
m = aL + (1/2)bL²
Therefore, the mass of the rod in terms of a, b, and L is m = aL + (1/2)bL².
(a) In this problem, rho (ρ) represents linear density, which has units of mass per length. In SI units, mass is measured in kilograms (kg) and length in meters (m). Therefore, the units of linear density are kg/m. Since ρ = a + bx, the units of a and b must be consistent with this equation. The units of a are the same as those of ρ, so a has units of kg/m. For b, since it is multiplied by x (which has units of meters), b must have units of kg/m² to maintain consistency in the equation.
(b) To find the mass of the rod, we need to integrate the linear density function over the length of the rod (from x=0 to x=L). Let's set up the integral:
Mass (M) = ∫(a + bx) dx, with limits from 0 to L
Now, we can integrate:
M = [a * x + (b/2) * x²] evaluated from 0 to L
Substitute the limits:
M = a * L + (b/2) * L²
So, the mass of the rod in terms of a, b, and L is:
M = aL + (bL²)/2
To learn more about density visit;
https://brainly.com/question/29775886
#SPJ11
1
6
the fourths and sixths are
1
7
In this picture of
4
subdivided further.
What do you notice, with these new subdivisions?
Answers
You are designing an aquarium for your new office. The dimensions of the aquarium are
restricted as shown in the diagram. You need the aquarium to hold 8820 cubic inches of
water. What is the shortest possible height (in inches) of the aquarium?
Answers
The shortest possible height of the aquarium is given as follows:
18 inches.
How to obtain the volume of a rectangular prism?The volume of a rectangular prism, with dimensions length, width and height, is given by the multiplication of these dimensions, according to the equation presented as follows:
Volume = length x width x height.
The dimensions for this problem are given as follows:
h = w + 4, w and 49 - w.
Hence the equation for the volume is given as follows:
w(w + 4)(49 - w) = 8820
w³ - 45w² - 196w + 8820 = 0.
Inserting the equation into a cubic equation calculator, the smallest value of w is:
w = 14.
Hence the smallest height is of:
w + 4 = 18 inches.
Missing InformationThe aquarium is given by the image presented at the end of the answer.
More can be learned about the volume of a rectangular prism at brainly.com/question/22070273
#SPJ1

The equation of a function and the graph of a different function are given below. Compare
the domain and range of each.
f(x)= 2√x

Answers
The domain of graphed function is start from -2, domain of f(x) is contain all positive numbers and both functions goes to infinity.
What is domain of a function?
A function's domain is the collection of all potential inputs. For instance, all real numbers are in the domain of f(x) = x^2, and all real numbers are in the domain of g(x)=1/x, with the exception of x = 0. Special functions with more constrained domains can also be defined.
We have to compare the domain of graphed function and the domain of function f(x) = 2√x.
The graphed function is start from -2 and goes to infinity.
So, the domain of graphed function is [-2, ∞).
Now consider, the function f(x) = 2√x
Since, the domain of square root function is the set of all non - negative real numbers.
So, the domain of f(x) is, (0, ∞).
Hence, the domain of graphed function is start from -2, domain of f(x) is contain all positive numbers and both functions goes to infinity.
To know more about domain of a function, click on the link
https://brainly.com/question/1369616
#SPJ1
An investment account with the same initial investment and the same APR has the most APY if the interested is compounded monthly daily annually continuously______O MonthlyO DailyO AnnuallyO Continuously
Answers
If the interest is compounded continuously, an investment account with the same initial investment and the same APR will have the highest APY.
APY (Annual Percentage Yield) is the effective annual rate of return after compounding. The higher the APY, the more frequently the interest is compounded.
Compounding yields the highest APY because it effectively provides an infinite number of compounding periods. Compounding daily, monthly, or annually yields lower APYs than compounding continuously.
An investment account is a type of financial product that allows people to save or invest money in the hopes of earning a profit. Individual retirement accounts (IRAs), brokerage accounts, savings accounts, and other types of investment accounts are available.
To learn more about Investment.
https://brainly.com/question/17252319
#SPJ4
3x +y = 3
2y = 10-6x
On a graph
Answers
Answer:
GRAPH OF 3x + y = 3 (written on attachment)
GRAPH OF 2y = 10 - 6x (written on attachment)


What is 1x1 divided by 3
Answers
Answer:
The answer to this one is 0.3333
Answer:
0.3333
Step-by-step explanation:
In your notebook, set up the following addition using a vertical format and find the sum of the given polynomials. 2mn 4n2 and 5m2 - 7mn 5 m2 5 mn - 4 n2 5 m2 - 14 mn - 4 n2 9 m2 9 mn - 4 n2 5 m2 - 5 mn 4 n2.
Answers
The sum of the polynomial is \(\rm 5m^2+4n^2-5mn\).
Given
In your notebook, set up the following addition using a vertical format and find the sum of the given polynomials.
Vertical Format:Write each polynomial below their like term and then combine it.
First expression: \(\rm 2mn+4n^2\)
Second Expression: \(\rm 5m^2-7mn\)
Now, we will add vertically. If the variable part of the term is the same then it would be like a term.
By using the vertical format the addition is;
\(\rm 2mn+4n^2+0m^2\)
\(\rm 5m^2-7mn+0n^2\)
Now, combine their coefficient and write the variable as same.
\(\rm -5mn+4n^2+5m^2\)
We can rearrange the term according to options.
\(\rm 5m^2+4n^2-5mn\)
Hence, the sum of the polynomial is \(\rm 5m^2+4n^2-5mn\).
To know more about Vertical format click the link given below.
https://brainly.com/question/10682697
the lower limit for the standard deviation is 0, the upper limit is: _______
Answers
The lower limit for the standard deviation is always 0, while the upper limit depends on the data and its distribution.
The standard deviation is a measure of the spread or dispersion of a set of data. It is defined as the square root of the variance, which is the average of the squared differences between each data point and the mean of the data. Since the variance involves squaring the differences, it is always positive or zero. Therefore, the standard deviation cannot be negative and has a lower limit of 0.
The upper limit of the standard deviation depends on the data and its distribution. In general, the standard deviation cannot be greater than the range of the data, which is the difference between the maximum and minimum values. For example, if the range of the data is 10 and the standard deviation is 15, then there must be an error or some issue with the data.
However, in some cases, the standard deviation can be much larger than the range of the data. This can happen if the data is highly skewed or has outliers. Skewed data is when the distribution of the data is not symmetrical, and most of the data falls on one side of the mean. In this case, the standard deviation may be much larger than the range of the data, as it takes into account the extreme values.
Outliers are data points that are much larger or smaller than the rest of the data. They can have a significant effect on the standard deviation, as they increase the variability of the data. In some cases, outliers may be errors or anomalies that should be removed from the data set before calculating the standard deviation.
In summary, the lower limit of the standard deviation is always 0, while the upper limit depends on the data and its distribution. In general, the standard deviation cannot be greater than the range of the data, but it can be much larger if the data is highly skewed or has outliers. It is important to consider the context of the data and any potential issues before interpreting the standard deviation.
To learn more about variance click here, brainly.com/question/31432390
#SPJ11
which point is located on the line represented by the equation y 4 = –5(x – 7)?
Answers
The correct answer to this question is the point (0, 39).
The equation of a line can be expressed in the slope-intercept form of a line, which is y = mx + b.
Here, the line is represented by y - 4 = -5(x - 7).
So, let's convert this equation to slope-intercept form: y - 4 = -5x + 35y = -5x + 39
Comparing it with the slope-intercept form, we can say that the slope of this line is -5 and the y-intercept is 39.
Thus, the line passes through the point (0, 39) and has a slope of -5.
Now, let's consider the equation of this line: y = -5x + 39
We can plug in different values of x and find the corresponding values of y to get different points on this line.
For example, when x = 0, we get: y = -5(0) + 39y = 39
So, the point (0, 39) is located on the line represented by the equation y - 4 = -5(x - 7).
Therefore, the answer to this question is the point (0, 39).
know more about slope-intercept
https://brainly.com/question/4015585
#SPJ11
What is the probability of selecting a king or queen from a standard deck of 52 cards
Answers
Solve for z.
Assume the equation has a solution for z.
a⋅(t+z)=45z+67
Answers
\(a(t+z)=45z+67\implies at+az=45z+67\implies az=45z+67-at \\\\\\ az-45z=67-at\implies \stackrel{common~factoring}{z(a-45)}=67-at\implies z=\cfrac{67-at}{a-45}\)
Athlete endorsers are often viewed as role models and expected to portray positive character traits while maintaining high moral standards, though in recent years, some athletes have rebelled against this notion. However, in some cases, teams, organizations, and brands will be willing to overlook moral or ethical blunders and character issues if a player is popular with the target audience. What is your opinion about the moral, ethical, and character standards in place for athlete endorsers? Drawing on the tenets of a Christian worldview (CWV) perspective, what would you do if you were asked to sign an athlete endorser with questionable character or moral and ethical values that were in conflict with your own?
Answers
In such a situation, I would choose not to endorse the athlete.
From a Christian worldview perspective, moral, ethical, and character standards hold significant importance. Athlete endorsers, as role models, should strive to uphold positive character traits and high moral standards. However, it is evident that in recent years, some athletes have challenged this notion.
When faced with the decision to sign an athlete endorser with questionable character or conflicting moral and ethical values, it is crucial to prioritize one's own values and beliefs. As a Christian, I would consider the impact of endorsing such an athlete on my personal integrity, as well as the message it sends to others.
It is essential to remain true to one's own moral compass and avoid promoting behavior that goes against Christian values. By doing so, I would be staying consistent with my beliefs and upholding the standards I hold dear.
Know more about the endorse
https://brainly.com/question/22697763
#SPJ11
Show work. Thanks
If h(x) = √3 + 2f'(x), where f(5) = 3 and f'(5) = 2, find h'(5) = ___
Answers
The derivative of h(x) with respect to x is zero, so h'(5) = 0. The explanation highlights the substitution of values and the differentiation of the function h(x) to obtain the result h'(5) = 0.
To find h'(5), we need to differentiate the function h(x) with respect to x and then evaluate it at x = 5.
Given h(x) = √3 + 2f'(x), we know that f'(x) represents the derivative of the function f(x).
Since we are given f'(5) = 2, we can substitute this value into the expression for h(x):
h(x) = √3 + 2(2)
Simplifying, we have:
h(x) = √3 + 4
Now, to find h'(5), we need to differentiate h(x) with respect to x:
h'(x) = 0 + 0
Differentiating a constant term such as √3 or 4 yields zero, as it does not vary with x.
Therefore, h'(5) = 0.
To learn more about derivative click here:
brainly.com/question/29144258
#SPJ11
Find the value of x. Assume that lines which appear to be tangent to the circle are tangent. A) 1 B) 3 C) 4 D) 6

Answers
Answer: D
Step-by-step explanation:
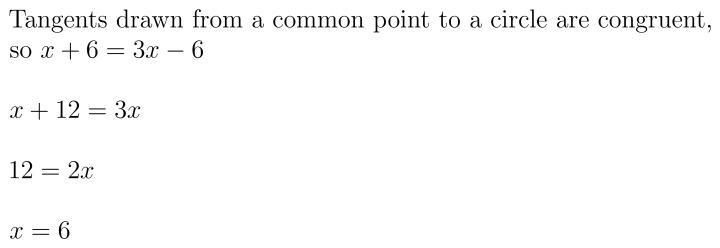
Help the girl out if you know it ASAP and explain!!

Answers
Out of the numbers 1,5,5,6,8 which is the mad
Answers
The mean absolute deviation from the given data set is 1.6
What is a Mean Absolute Deviation?The mean absolute deviation measures how far the data points are on average from a center point. Mean, median, mode, or any other random figure can serve as the center point.
The mean is frequently used as the center point, In this situation, The method for computing mean absolute deviation (MAD) is helpful, which represents the average of the absolute departure of the data points from the mean of the data set.
Mean = (1+5+5+6+8)/5
Mean = 25/5
Mean = 5
The distance of each value from the mean is as follows:
Value distance from the mean 5
1 4
5 0
5 0
6 1
8 3
MAD = (4 + 0 + 0 + 1 + 3)/5
MAD = 8/5
MAD = 1.6
Learn more about Mean Absolute Deviation here:
https://brainly.com/question/3250070
#SPJ1
K-15 over 7 equals -1
Answers
Answer:
8
Step-by-step explanation:
8-15=-7
-7/7=-1
There are 9 people going on a trip. They purchased coach tickets for $160, and first class tickets for $1180. The total budget to spend was $4500. How many first class tickets did they buy? How many Coach tickets did they buy? Show your work. Brainliest for Right answer
Answers
Answer: 6 Coach Tickets and 3 First Class tickets
Step-by-step explanation:
Add 160 to 1180 until you get 4500
Helpppppp and explain tooo thank you :)

Answers
Answer:
{5, 6, 7}
Step-by-step explanation:
When we have a given relation, the domain is the set of inputs, and the range as the set of the outputs.
so for a function f(x), and a domain {a. b. c}
The range is:
{f(a), f(b), f(c)}
In this case, we have:
f(x) = x + 6
and the domain is {-1, 0, 1}
Then the range is:
{ f(-1), f(0), f(1) }
{-1 + 6, 0 + 6, 1 + 6}
{5, 6, 7}
The correct option is the third one.
the equation of line p is y= -7/8x + 3/2. line q is parallel to line p. what is the slope of line q?
Answers
Answer:
-7/8
Step-by-step explanation:
If two lines are parallel, they have the same slope. The slope of p is -7/8 (y=mx+b), so the slope of q is also -7/8.
the line contains the point (3, 5) and is parallel to the line containing (-4, 0) and (-1, -2)
Answers
To find the equation of the line passing through (3, 5) and parallel to the line containing (-4, 0) and (-1, -2), we need to use the slope-intercept form of a line:
y = mx + b
where m is the slope of the line and b is the y-intercept.
First, we need to find the slope of the line containing (-4, 0) and (-1, -2):
m = (y2 - y1) / (x2 - x1)
m = (-2 - 0) / (-1 - (-4))
m = -2 / 3
Since the line we're looking for is parallel to this line, it will have the same slope.
Now we can use the point-slope form of a line to find the equation of the line passing through (3, 5) with slope -2/3:
y - y1 = m(x - x1)
y - 5 = (-2/3)(x - 3)
Simplifying and rearranging, we get:
y = (-2/3)x + 7
So the equation of the line containing the point (3, 5) and parallel to the line containing (-4, 0) and (-1, -2) is y = (-2/3)x + 7.
I Believe This is the answer
Answer: The line through (-4, -6, 1) and (-2, 0, -3), is parallel to the line through (10, 18, 4) and (5, 3, 14).
Step-by-step explanation:
Have a Great Day
Find the quotient of the complex numbers. Express your answer in trigonometric form.
z1=5(cos25∘+i sin25∘)
z2=2(cos80∘+i sin80∘)
A. 10(cos105∘+i sin105∘)
Answers
The quotient of the complex numbers z1 and z2, expressed in trigonometric form, is 2.5(cos55° - i sin55°).
To find the quotient of the complex numbers z1 and z2, we can divide z1 by z2. Let's go step by step:
z1 = 5(cos25° + i sin25°)
z2 = 2(cos80° + i sin80°)
To divide complex numbers, we multiply the numerator and denominator by the conjugate of the denominator. The conjugate of a complex number is obtained by changing the sign of the imaginary part.
The conjugate of z2 is:
conjugate(z2) = 2(cos80° - i sin80°)
Now, let's multiply z1 and the conjugate of z2:
z1 * conjugate(z2) = 5(cos25° + i sin25°) * 2(cos80° - i sin80°)
To simplify the multiplication, we can use the trigonometric identity:
cos(a)cos(b) - sin(a)sin(b) = cos(a - b)
Applying this identity, we have:
z1 * conjugate(z2) = 10(cos(25° - 80°) + i sin(25° - 80°))
Simplifying further:
z1 * conjugate(z2) = 10(cos(-55°) + i sin(-55°))
Since cos(-x) = cos(x) and sin(-x) = -sin(x), we can rewrite it as:
z1 * conjugate(z2) = 10(cos55° - i sin55°)
Finally, to express the quotient of the complex numbers in trigonometric form, we divide z1 * conjugate(z2) by the squared magnitude of z2 (the magnitude squared is equal to the product of the number and its conjugate):
Quotient = (z1 * conjugate(z2)) / (z2 * conjugate(z2))
The magnitude of z2 is 2, so the squared magnitude is 2^2 = 4.
Quotient = (10(cos55° - i sin55°)) / 4
Simplifying the quotient:
Quotient = 2.5(cos55° - i sin55°)
Therefore, the quotient of the complex numbers z1 and z2, expressed in trigonometric form, is 2.5(cos55° - i sin55°).
Know more about trigonometric form here:
https://brainly.com/question/12517327
#SPJ11
Complete the point-slope equation of the line through (1,-1) and
(5,2).
Use exact numbers.
y- (-1) =
Answers
An equation in point-slope form that can be used to describe the relationship between x and y is y - (-1) = 3/4(x - 1).
How to determine an equation of this line?In Mathematics and Geometry, the point-slope form of a straight line can be calculated by using the following mathematical equation (formula):
y - y₁ = m(x - x₁)
Where:
x and y represent the data points.m represent the slope.First of all, we would determine the slope of this line;
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
Slope (m) = (2 + 1)/(5 - 1)
Slope (m) = 3/4
At data point (1, -1) and a slope of 3/4, a linear equation for this line can be calculated by using the point-slope form as follows:
y - y₁ = m(x - x₁)
y - (-1) = 3/4(x - 1)
y + 1 = 3/4(x - 1)
Read more on point-slope here: brainly.com/question/24907633
#SPJ1