The graph below represents the total shipping cost of x items for four different companies.
Shipping Charges
A graph has number of items on the x-axis and shipping cost in dollars on the y-axis. Line W goes through points (0, 5) and (2, 13). Line U goes through (0, 12) and (3, 16). Line Y goes through (0, 10) and (2, 12). Line Z goes through (0, 0) and (2, 4).
Which list places the companies in order from the steepest slope to the least steep slope?
Answers
Answer:
A.W, Z, U, Y
Step-by-step explanation:
I got it right on the edge quiz
Comment Cheese if your sMiLiN
Answer:
A.W, Z, U, Y
Step-by-step explanation:
i got the answer right on the quiz :)
Related Questions
Ashley needs a 4.6 yards of chain to hang some flower baskets the chain is sold by meter how many meters does Ashley need
Answers
12. For each case, give two examples of a calculation with two numbers.
a. The inputs are not positive integers, but the result is a positive integer.
b. The inputs are not integers, but the result is an integer.
c. The inputs are not rational numbers, but the result is a rational number.
d. The inputs are not real numbers, but the result is a real number.
Answers
a. (2/3) ÷ (1/4) = 8/3
√(27) ÷ √(3) = 3
b. (4.5) × (4) = 18
(3.6) ÷ (0.6) = 6
c. (√2) × (√8) = 4√2
(π) ÷ (e) = a irrational number but multiplied by an integer such as 2π/e would yield a rational number.
d. (3+4i) × (3-4i) = 25
log(-8) + log(2) = log(16) (using complex logarithms)
What are the examples?a. The first example, (2/3) ÷ (1/4) = 8/3, is an example where the inputs are not positive integers, but the result is a positive integer. This is because when we divide two fractions, we actually multiply the first fraction by the reciprocal of the second fraction. So, (2/3) ÷ (1/4) is the same as (2/3) × (4/1) = 8/3, which is a positive integer.
Therefore, For the second example, √(27) ÷ √(3) = 3, we can simplify the square root of 27 as √(3 × 9) = √3 × √9 = 3√3. Similarly, we can simplify the square root of 3 as √(3 × 1) = √3 × √1 = √3. Then, we can divide √(27) by √(3) to get 3√3 ÷ √3 = 3, which is a positive integer.
Read more about positive integers here:
https://brainly.com/question/1367050
#SPJ1
What is the third term of the recursive sequence below

Answers
Given the sequence:
\(\begin{gathered} a_1=-6 \\ a_n=\frac{1}{2}a_{n-1}-n \end{gathered}\)Let's find the third term of the sequence.
To find the third term, a3, we have:
First find the second term, a2:
\(\begin{gathered} a_2=\frac{1}{2}a_{2-1}-2 \\ \\ a_2=\frac{1}{2}a_1-2 \\ \\ a_2=\frac{1}{2}(-6)-2 \\ \\ a_2=-3-2 \\ \\ a_2=-5 \end{gathered}\)The second term is -5.
To find the third term, we have:
\(\begin{gathered} a_3=\frac{1}{2}a_{3-1}-3 \\ \\ a_3=\frac{1}{2}a_2-3 \\ \\ a_3=\frac{1}{2}(-5)-3 \\ \\ a_3=-2.5-3 \\ \\ a_3=-5.5 \end{gathered}\)Therefore, the third term of the
Make sure to Show your math steps to arrive at your answers and Explain each step in complete sentence please

Answers
Answer:
Min is 51 and max is 75 and the the mediem is 63 and the q1 is 54 and q2 is 55 and 57 and q3 is 65 and 69
Step-by-step explanation:
the least is 51 and the most is 75 and the mean is 63 if u list them in order and than u find the quartiles that are between the median and 51 and q3 is between the median and the max.
find the length of the line segment whose endpoints are (-5,6) and (6,6)
Answers
Answer: 11 units
Step-by-step explanation:
Use the distance formula: \(\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2} }\)
\((x_{1}, y_{1})=(-5, 6)\\(x_{2}, y_{2})=(6, 6)\\\\\sqrt{(6-(-5)^{2}+(6-6)^{2}} =\sqrt{(11)^{2}+(0)^{2}} =\sqrt{121+0}=\sqrt{121}=11\)
The length of the line is 11 units.
What is distance?The distance between two points is the length of the line joining the two points.
Formula: distance= √(x_2-x_1)²+(y_2-y_1)²
Given that, endpoints are (-5,6) and (6,6) of the line segment.
The length= √(6+5)²-(6-6)²
=11 units
To learn more on Distance click:
https://brainly.com/question/15172156
#SPJ2
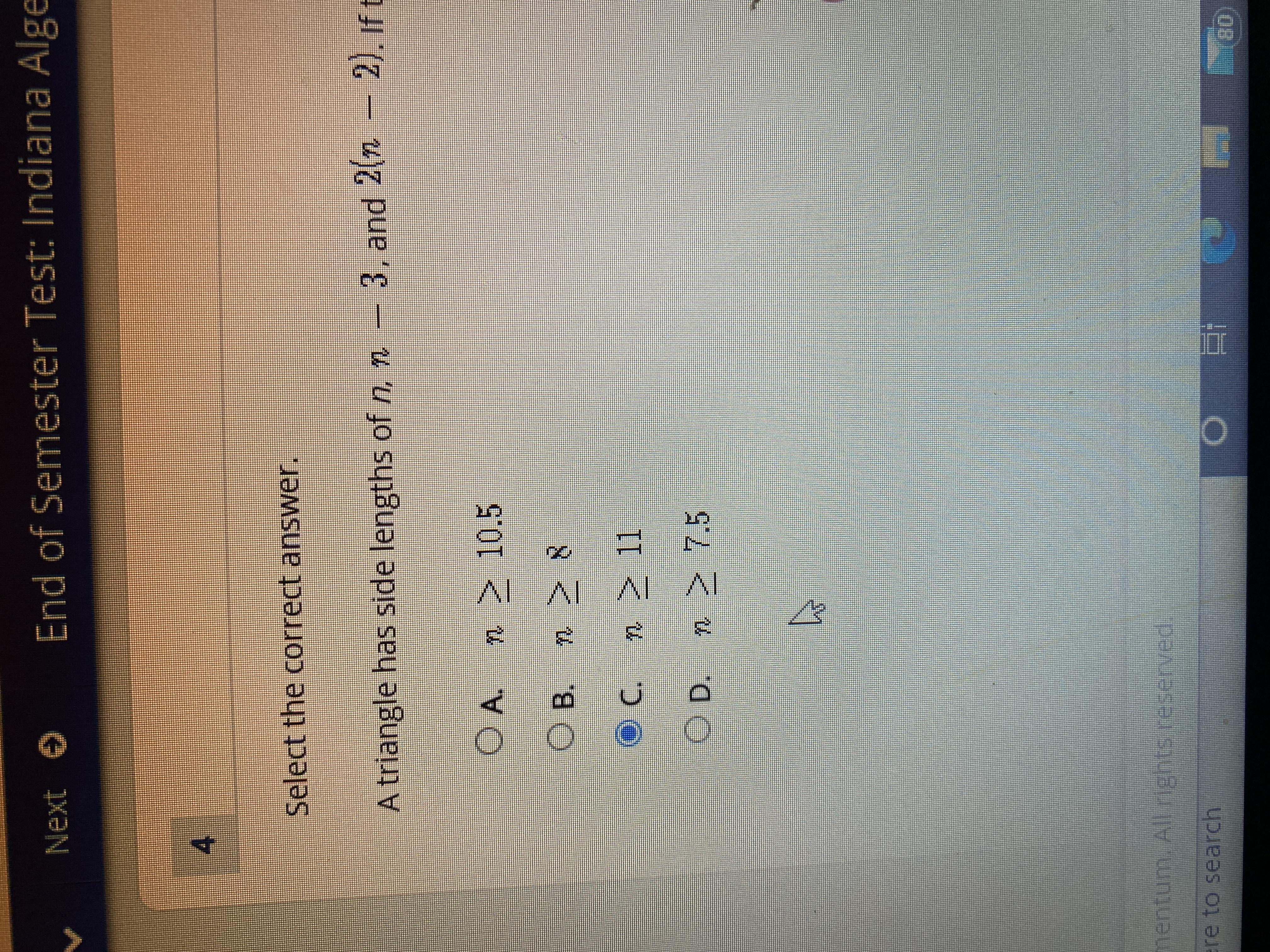
A triangle has side lengths of n, n - 3, and 2(n – 2). If the perimeter of the triangle is at least 37 units, what is the value of n?
A. m > 11
B. 1 > 7.5
C.n> 10.5
D. n>8
Answers
Answer:
Step-by-step explanation:
Some steps to construct an angle MNT congruent to angle PQR are listed below. Step 3 is not listed:
Step 1: Use a compass to draw an arc from point Q which intersects the side PQ at point A and the side QR at point B.
Step 2: Draw a segment NT and use the same width of the compass to draw an arc from point N which intersects the segment NT at a point X.
Step 3:
Step 4: Join points N and Y using a straightedge.
Which statement describes step 3 correctly?)
A. Adjust the width of the compass to AQ, and draw an arc from point X such that it intersects the arc drawn from N in a point Y.
B. Adjust the width of the compass to NX, and draw an arc from point X such that it intersects the arc drawn from N in a point Y.
C. Adjust the width of the compass to BQ, and draw an arc from point X such that it intersects the arc drawn from N in a point Y.
D. Adjust the width of the compass to AB, and draw an arc from point X such that it intersects the arc drawn from N in a point Y.
Answers
The correct statement describing step 3 is:
C. Adjust the width of the compass to BQ, and draw an arc from point X such that it intersects the arc drawn from N in a point Y.
Correct option is C.
In the given construction,
step 1 involves drawing an arc from point Q to intersect the sides PQ and QR at points A and B, respectively.
Step 2 involves drawing a segment NT and using the same width of the compass to draw an arc from point N to intersect the segment NT at point X.
To continue the construction and construct an angle MNT congruent to angle PQR,
step 3 requires adjusting the width of the compass to BQ. This means the compass should be set to the distance between points B and Q. Then, from point X, an arc is drawn that intersects the arc drawn from N at a point Y.
By completing this step, the construction creates an angle MNT that is congruent to the given angle PQR.
Correct option is C.
For more questions on intersects
https://brainly.com/question/28744045
#SPJ8
Given the discrete uniform population: 1 fix} = E El. elseweltere .x=2.4ifi. Find the probability that a random sample of size 511, selected with replacement, will yield a sample mean greater than 4.1 but less than 4.11. Assume the means are measured to the any level of accuracy. {3 Points}.
Answers
The probability of obtaining a sample mean between 4.1 and 4.11 in a random sample of size 511 is 0.
To calculate the probability that a random sample of size 511, selected with replacement, will yield a sample mean between 4.1 and 4.11 in a discrete uniform population with x = 2.4, we can use the properties of the sample mean and the given population.
In a discrete uniform population, all values are equally likely. Since the mean of the population is x = 2.4, it implies that each value in the population is 2.4.
The sample mean is calculated by summing all selected values and dividing by the sample size. In this case, the sample size is 511.
To find the probability, we need to calculate the cumulative distribution function (CDF) for the sample mean falling between 4.1 and 4.11.
Let's denote X as the value of each individual in the population. Since X is uniformly distributed, P(X = 2.4) = 1.
The sample mean, denoted as M, is given by M = (X1 + X2 + ... + X511) / 511.
To find the probability P(4.1 < M < 4.11), we need to calculate P(M < 4.11) - P(M < 4.1).
P(M < 4.11) = P((X1 + X2 + ... + X511) / 511 < 4.11)
= P(X1 + X2 + ... + X511 < 4.11 * 511)
Similarly,
P(M < 4.1) = P(X1 + X2 + ... + X511 < 4.1 * 511)
Since each value of X is 2.4, we can rewrite the probabilities as:
P(M < 4.11) = P((2.4 + 2.4 + ... + 2.4) < 4.11 * 511)
= P(2.4 * 511 < 4.11 * 511)
Similarly,
P(M < 4.1) = P(2.4 * 511 < 4.1 * 511)
Now, we can calculate the probabilities:
P(M < 4.11) = P(1224.4 < 2099.71) = 1 (since 1224.4 < 2099.71)
P(M < 4.1) = P(1224.4 < 2104.1) = 1 (since 1224.4 < 2104.1)
Finally, we can calculate the probability of the sample mean falling between 4.1 and 4.11:
P(4.1 < M < 4.11) = P(M < 4.11) - P(M < 4.1)
= 1 - 1
= 0
Therefore, the probability that a random sample of size 511, selected with replacement, will yield a sample mean between 4.1 and 4.11 in the given discrete uniform population is 0.
Learn more about Probability click here :brainly.com/question/30034780
#SPJ11
describe the graph of the solution

Answers
First, we want to note two things:
We have a solid circle at -10, so -10 IS part of the solution.We have shading to the right of -10, meaning we also need to include numbers to the right of -10, or numbers greater than -10.
We can describe this with an inequality: x ≥ -10
Be sure you use ≥ and not >, since -10 is included.
We can describe this with interval notation: [ -10, infty )
Be sure you use [ and not ( on -10, since -10 is included.
You can also use set-builder notation: { x | x ≥ -10 }
Question in the picture

Answers
Answer:
19
Step-by-step explanation:
Given m is parallel to N:
The sum of given agles is equal to 180 since they are supplementary
8x - 7 + x + 16 = 180 add like terms
9x + 9 = 180 subtract 9 from both sides
9x = 171 divide both sides by 9
x = 19
Use Wallis's Formulas to evaluate the integral. Integral^pi/2 _0(cos(x))7 dx
Answers
To evaluate the integral using Wallis's Formula, we need to find the integral of cos^7(x) from 0 to π/2. Wallis's Formula is given by:
∫(0 to π/2) cos^n(x) dx = (n-1)/n * (n-3)/(n-2) * ... * (1 or 2)/(n+1 or n) * (π/2)
For our problem, we have n = 7, so we'll apply the formula as follows:
∫(0 to π/2) cos^7(x) dx = (7-1)/7 * (7-3)/(7-2) * 1/8 * (π/2) = 6/7 * 4/5 * 1/8 * (π/2)
Now, let's simplify the expression: = 24/35 * π/4 = 6π/35
So, the value of the integral is 6π/35.
To evaluate this, we use the definition of the Beta function: B(a,b) = Gamma(a) * Gamma(b) / Gamma(a+b).
where Gamma is the Gamma function. So, we have: B(4,1/2) = Gamma(4) * Gamma(1/2) / Gamma(9/2).
Using the fact that Gamma(1/2) = sqrt(pi), we can simplify: B(4,1/2) = 3 * sqrt(pi) / 16, Finally, we substitute this back into the original expression: Integral from 0 to pi/2 of (cos(x))^7 dx = (1/2) * B(4, 1/2) = 3 * sqrt(pi) / 32, So the value of the integral is 3 * sqrt(pi) / 32.
To know more about value click here
brainly.com/question/30760879
#SPJ11
A family that is known to have two children is selected at random
from amongst all families with two children. Find the probability that
both children are boys, given that there is a boy in this family. Please help me solve this problem.
Answers
Answer: one outta a mil
Step-by-step explanation:
Please help! I will mark as brainliest IF answer is right. <3

Answers
Answer:
y=-1/6x-13/3
Step-by-step explanation:
first we find the slope
y1-y2/x1-x2
-3+5/-8+4
1/-6
now we find y intersept
-3=-1/6(-8)+b
-3=8/6+b
-13/3=b
you plug it in y = mx+b
y=-1/6x-13/3
What is sine in geometry for a right triangle
Answers
Answer:
The ratio of the length opposite to the side of the triangle whose angle is opposite to the length of the hyptoneuse.
A county reported the following data on breast cancer for the past year. what is the prevalence rate per 100,000? number of new cases: 1,774; number of total cases: 4,192; population: 5,977,906
Answers
The prevalence rate per 100,000 is 99.8%
We know that the prevalence rate is the proportion of persons in a population who have a particular disease over a specified period of time.
In this question, we have been given a data on breast cancer for the past year:
number of new cases: 1,774;
number of total cases: 4,192;
population: 5,977,906
We need to find the prevalence rate per 100,000
The total number of infected people = 1,774 + 4192
= 5966
Chance of infection in the whole population would be,
5,977,906/ 5966 ≈ 1002
This means, chances of having breast cancer is 1 in every 1002 people.
A prevalence rate is calculated by dividing total number of infected people by the total population. The result is then multiplied by 100,000
Now we calculate the prevalence rate per 100,000
= (5966 / 5,977,906) × 100,000
= 0.000998 × 100,000
= 99.8 %
Therefore, the prevalence rate per 100,000 is 99.8%
Learn more about the prevalence rate here:
https://brainly.com/question/14739993
#SPJ4
Ricky's football team scored only 15 times this season.
Every touchdown gave them 7 points (they missed no extra
points) and each field-goal gave them 3 points. They scored 77
points (total) this season.
TRUE OR FALSE:

Answers
Answer:
False 15 times 7= 105
Please help this is urgent!! Will mark brainliest!

Answers
Answer:
C
Step-by-step explanation:
2·π·6·10+2·π·6^2
Answer:
602.88 in^2
Step-by-step explanation:
A=2πrh+2πr^2
A=2(3.14)(6)(10)+2(3.14)(6^2)
A=376.8+226.08
A=602.88
Evaluate the expression shown for x = 9.
-5/6x +7.
A.-13 1/3.
B.-1/2.
C.7 1/3.
D.9 2/3
Answers
Answer:
B. 1/2
Step-by-step explanation:
Make 9 an improper fraction, then multiply by -5/6.
-5/6 times 9/1 = -45/6.
-45/6 cannot be simplified, so you make it a mixed number.
-7 1/2.
Add the 7 to -7 1/2 and that cancels out to 1/2
A paper cup in the shape of a cone has a radius of 6 cm and is 5 cm high. What is the volume of the cup ?
Answers

If angle cde is a straight angle and de bisects gdh and angle gde =8x-1 angle edh =6x+15 and angle cdf +43 find each measure
Answers
the measures of the angles are:
Angle GDE = 69.2856 degrees
Angle EDH = 67.7142 degrees
Angle CDF = 43 degrees
To solve this problem, we can start by using the given information to set up an equation.
We know that angle CDE is a straight angle, which means it measures 180 degrees. Additionally, angle DEH bisects angle GDH, which means angles GDE and EDH are equal.
Let's denote the measure of angle GDE as A and the measure of angle EDH as A.
Given:
Angle GDE = 8x - 1
Angle EDH = 6x + 15
Angle CDF = 43
Since angle CDE is a straight angle, we have the equation:
Angle GDE + Angle EDH + Angle CDF = 180
Substituting the given values into the equation, we get:
(8x - 1) + (6x + 15) + 43 = 180
Combine like terms:
14x + 57 = 180
Subtract 57 from both sides:
14x = 123
Divide by 14:
x = 8.7857
Now, we can substitute this value of x back into the given angles to find their measures:
Angle GDE = 8x - 1
= 8(8.7857) - 1
= 70.2856 - 1
= 69.2856
Angle EDH = 6x + 15
= 6(8.7857) + 15
= 52.7142 + 15
= 67.7142
Angle CDF = 43
learn more about straight angle here:
https://brainly.com/question/11367993
#SPJ11
Please help!!
the function of C gives the percentage of homes using only cell phone service X years after 2004 explain the meaning of each statement.
1. C(10)=35
2. C(x) = 10
3. how is C(10) different from C(x) = 10?
Answers
Answer:
Step-by-step explanation:
1. C(10)=35 is the percentage of homes using only cell phone service 10 years after 2004, that is, after 2014.
2. C(x) = 10 is the percentage of homes using only cell phone service x years after 2004. We must find x.
3. how is C(10) different from C(x) = 10?
In C(10), 10 measures time in years and is the independent variable here; C10) is the dependent variable. See (2), above. In C(x), x is the (unknown) independent variable, whereas 10 is the output vaue, the dependent variable.
Which point does not pass through?
10 Points

Answers
Answer:
C ( 9 , 15)
Step-by-step explanation:
Which graph shows a function and its?
Answers
The graph shows a function and its is the graph in option A.
What is inverse function and their graphs?The original path is reflected on the line y = x. The two functions are said to be inverses of one another if the graphs of both functions are symmetric with respect to the line y = x. This is due to the fact that (y, x) lies on the inverse function of the function if (x, y) lies on the original function.
The inverse function is shown on a graph with the use of a vertical line test. The line has a slope and travels through the origin.
Instance is the f(x) = 2x + 5 = y. Then, is the inverse of \(g(y) = \frac{ (y-5)}{2} = x\) f(x).Reflecting over the y and x gives us the function of the inverse.
Learn more about graph at:
https://brainly.com/question/19227104
#SPJ4


A bouncy ball is dropped such that the height of its first bounce is 4.5 feet and each successive bounce is 73% of the previous bounce's height. What would be the height of the 10th bounce of the ball? Round to the nearest tenth (if necessary).
Answers
The height of the 10th bounce of the ball will be 0.6 feet.
What is geometric sequence?A geometric sequence is a sequence in which each term is found by multiplying the preceding term by the same value.
What is the formula for finding the nth term of geometric sequence?The nth term of the geometric sequence is given by
\(\sf T_n=ar^{n-1}\)
Where,
\(\sf T_n\) is the nth term.r is the common ratioa is the first termAccording to the given question.
During the first bounce, height of the ball from the ground, a = 4.5 feet
And, the each successive bounce is 73% of the previous bounce's height.
So,
During the second bounce, the height of ball from the ground
\(\sf = 73\% \ of \ 10\)
\(=\dfrac{73}{100}(10)\)
\(\sf = 0.73 \times 10\)
\(\sf = 7.3 \ feet\)
During the third bounce, the height of ball from the ground
\(\sf = 73\% \ of \ 7.3\)
\(=\dfrac{73}{100}(7.3)\)
\(\sf = 5.33 \ feet\)
Like this we will obtain a geometric sequence 7.3, 5.33, 3.11, 2.23,...
And the common ratio of the geometric sequence is 0.73
Therefore,
The sixth term of the geometric sequence is given by
\(\sf T_{10}=10(0.73)^{10-1\)
\(\sf T_{10}=10(0.73)^{9\)
\(\sf T_{10}=10(0.059)\)
\(\sf T_{10}=0.59\thickapprox0.6 \ feet\)
Hence, the height of the 10th bounce of the ball will be 0.6 feet.
Find out more information about geometric sequence here:
brainly.com/question/11266123
simplify [2/x²-5x+6] - [5/x-2]
Answers
Answer
When simplified, the answer is
\(\frac{-5x+17}{x^2-5x+6}\)Explanation
[2/x² - 5x + 6] - [5/x - 2]
\(\frac{2}{x^2-5x+6}-\frac{5}{x-2}\)To solve this, we need to first factorize x² - 5x + 6
x² - 5x + 6
= x² - 3x - 2x + 6
= x (x - 3) - 2 (x - 3)
= (x - 3) (x - 2)
So, we can rewrite the question, and then take an LCM
\(\begin{gathered} \frac{2}{x^2-5x+6}-\frac{5}{x-2} \\ \frac{2}{(x-3)(x-2)}-\frac{5}{x-2} \end{gathered}\)We will then take the LCM
\(\begin{gathered} \frac{2}{(x-3)(x-2)}-\frac{5}{x-2} \\ =\frac{2-5(x-3)}{(x-3)(x-2)} \\ =\frac{2-5x+15}{(x-3)(x-2)} \\ =\frac{-5x+17}{(x-3)(x-2)} \\ =\frac{-5x+17}{x^2-5x+6} \end{gathered}\)Hope this Helps!!!
how does 9 + 9 = 6 ?
Answers
Answer:
it does not, it equals 18
Step-by-step explanation:
9+9=18 - true
9+9=6 - false
6. The coordinates of point A are given. The midpoint of AB is (3,-5). Find the coordinates of point B.
a. A(4,-8)
b. A(2.5, -6.5)
Answers
Midpoint = (x1 + x2)/2, (y1 + y2)/2
In this case, we are given that the midpoint of AB is (3,-5). We can substitute this into the midpoint formula to find the coordinates of point B.
Midpoint = (x1 + x2)/2, (y1 + y2)/2
= (3 - x1)/2, (-5 - y1)/2
We can then solve for x1 and y1, which are the coordinates of point A.
x1 = 23 - x2
y1 = 2(-5) - y2
Substituting the given coordinates of the midpoint into these equations, we get:
x1 = 6 - x2
y1 = -10 - y2
We are given that the coordinates of point A are (4,-8). Substituting these values into the equations above, we can solve for x2 and y2, which are the coordinates of point B:
x1 = 6 - x2
4 = 6 - x2
x2 = 2
y1 = -10 - y2
-8 = -10 - y2
y2 = -6
Therefore, the coordinates of point B are (2,-6). This means that the correct answer is option (a), A(4,-8).
Interchange the digits in hundreds and tens place in the number 54,150. Can you tell if the value of new number will increase or decrease and by how much?
Answers
Answer: Increases by 360
Step-by-step explanation:
The number in hundreds place is 1 and tens place is 5. If you interchange these numbers, you place 1 in the tens place and 5 in the hundreds place.
So, it would be 54,510.
The number is increases since the hundreds value is more now.
54,510 - 54,150 = 360
Increases by 360
Question is in the picture!!

Answers
From the graph given the constant of proportionality which is the intercept of the graph is 0.
Constant of proportionalityIn the slope - intercept equation , y = bx + C, the constant of proportionality is denoted as C which is also the intercept value of the graph.
The constant of proportionality doesn't change in an equation. For the graph attached , the point where the fitted line crosses the y-axis is the intercept which is 0.
Hence, the constant of proportionality is 0.
Learn more on constant of proportionality:https://brainly.com/question/1835116
#SPJ1
The Gallup Poll interviews 1600 people. Of these, 18% say that they jog regularly. The news report adds: "The poll has a margin of error of plus or minus three percentage points at a 95% confidence level." You can safely conclude that
A. 95% of all Gallup Poll samples like this one give answers within ±3% of the true population value.
B. the percent of the population who jog is certainly between 15% and 21%.
C. 95% of the population jog between 15% and 21% of the time.
D. we can be 95% confident that the sample proportion is captured by the confidence interval.
E. if Gallup took many samples, 95% of them would find that 18% of the people in the sample jog.
Answers
The correct answer is option D. We can be 95% confident that the sample proportion is captured by the confidence interval.
The margin of error of plus or minus three percentage points at a 95% confidence level means that the true proportion of people who jog regularly in the population is estimated to be between 15% and 21%. We can be 95% confident that the true proportion of people who jog regularly falls within this interval.
Therefore, option B is correct. Option A is incorrect because it implies that the margin of error always holds true for any sample size, which is not the case. Option C is incorrect because it presents a range of values for the population, not for the estimate. Option E is incorrect because it refers to the proportion of samples that would find the same sample proportion, not the range of values within which the true proportion lies.
Learn more about Confidence Level:
https://brainly.com/question/15712887
#SPJ4