Answers
Answer:
C. G(x) = x^3 - 5
Step-by-step explanation:
G(x) is the graph of F(x) shifted down 5 units.
Related Questions
Find the distance between the points P and Q shown.
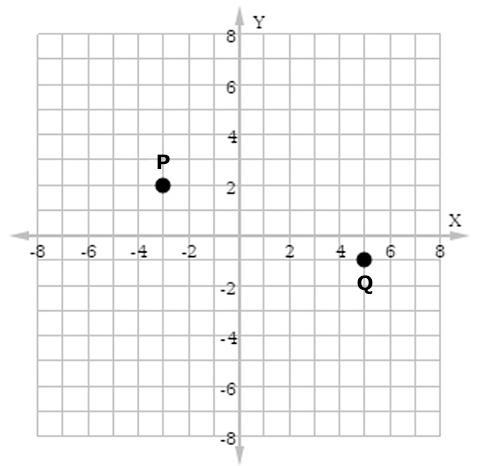

Answers
The distance between points P and Q is √73
How to find the distance between the two points?First, remember that the distance between two points whose coordinates are (a, b) and (c, d) is given by:
distance = √( (a - c)² + (b - d)²)
Here we can see that the coordinates of the two shown points are:
P = (-3, 2)
Q = (5, -1)
Replacing that in the distance formula we will get:
distance = √( (-3 - 5)² + (2 + 1)²)
distance = √( (-8)² + (3)²)
distance = √73
So the correct option is the third one.
Learn more about distance at:
https://brainly.com/question/7243416
#SPJ1
-16 + the quotient of a number and 2 is 35
Answers
Answer:
Step-by-step explanation:

algebra domain and range please help

Answers
Answer:
Option 2.
Step-by-step explanation:
Find the domain by finding where the function is defined. The range is the set of values that correspond with the domain.
Domain: \((- \infty} ,0)\) ∪ \((0, \infty} )\)
Range: \((- \infty} ,0)\)∪\((0, \infty} )\)
Seth is using the figure shown below to prove Pythagorean Theorem using triangle similarity:
In the given triangle ABC, angle A is 90° and segment AD is perpendicular to segment BC.
The figure shows triangle ABC with right angle at A and segment AD. Point D is on side BC.
Which of these could be a step to prove that BC2 = AB2 + AC2?
possible answers -
By the cross product property, AB2 = BC multiplied by BD.
By the cross product property, AC2 = BC multiplied by BD.
By the cross product property, AC2 = BC multiplied by AD.
By the cross product property, AB2 = BC multiplied by AD.

Answers
The correct step to prove that \(BC^2 = AB^2 + AC^2\) is:
By the cross product property, \(AC^2 = BC \cdot AD\).
To prove that \(BC^2 = AB^2 + AC^2\), we can use the triangle similarity and the Pythagorean theorem. Here's a step-by-step explanation:
Given triangle ABC with right angle at A and segment AD perpendicular to segment BC.
By triangle similarity, triangle ABD is similar to triangle ABC. This is because angle A is common, and angle BDA is a right angle (as AD is perpendicular to BC).
Using the proportionality of similar triangles, we can write the following ratio:
\($\frac{AB}{BC} = \frac{AD}{AB}$\)
Cross-multiplying, we get:
\($AB^2 = BC \cdot AD$\)
Similarly, using triangle similarity, triangle ACD is also similar to triangle ABC. This gives us:
\($\frac{AC}{BC} = \frac{AD}{AC}$\)
Cross-multiplying, we have:
\($AC^2 = BC \cdot AD$\)
Now, we can substitute the derived expressions into the original equation:
\($BC^2 = AB^2 + AC^2$\\$BC^2 = (BC \cdot AD) + (BC \cdot AD)$\\$BC^2 = 2 \cdot BC \cdot AD$\)
It was made possible by cross-product property.
Therefore, the correct step to prove that \(BC^2 = AB^2 + AC^2\) is:
By the cross product property, \(AC^2 = BC \cdot AD\).
For more questions on cross-product property:
https://brainly.com/question/14542172
#SPJ8
What Did the Baby Porcupine Say
When It Backed Into a Cactus?
each
Answers
Answer:
As baby porcupine is backed into cactus, so the spines of cactus will feel like spines of mother porcupine. So the baby porcupine will give call to its mother.
Step-by-step explanation
He said hi Ma.
Juan rented 24 movies at $2.75
each. What was the total cost for
renting the movies?
Answers
Answer:
$66Step-by-step explanation:
each movie costs $2.75
there are 24 movies
24 x 2.75
=66
total cost=$66
Answer:
$66.
Step-by-step explanation:
All you need to do is $2.75 x 24 which equals to $66.00.
You can work this out by doing a long-multiplication method on paper or use a calculator.
Hope that helps. x
please help me I have zero clue what I'm doing!

Answers
Answer:
6
Step-by-step explanation:
10-4 is 6 and they are on the same x axis
a. Will he be able to make a right triangle with his fence? Why or why not?
Answers
Joel be not able to make a right triangle with his fence because the given dimensions are not satisfying for Pythagoras theorem.
What is Trigonometry?
Trigonometry is a branch of mathematics that studies relationships between side lengths and angles of triangles.
Dimensions of triangle he has to use for fencing are
15 feet, 8 feet, and 20 feet.
For making it a right triangle it must satisfy the "Pythagoras theorem" which states that
In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.
H²=B²+P²
20²=15²+18²
400=225+64
400≠289
No, it will not be able to make a right triangle.
Hence, Joel will be not able to make a right triangle with his fence because the given dimensions are not satisfying for pythagoras theorem.
To learn more on trigonometry click:
https://brainly.com/question/25122835
#SPJ9
The complete question is given below:
Joel wants to fence off a triangular portion of his yard for his chickens. The three pieces of fencing he has to use are 15 feet, 8 feet, and 20 feet long.
1. Will he be able to make a right triangle out of his fence? Why or why not?
A local road has a grade of 2%. The grade of a road is its slope expressed as a percent. Find the slope of the road as a fraction and then simplify.
Answers
Answer:
\(\frac{1}{50}\)
Step-by-step explanation:
2% = \(\frac{2}{100}\) = \(\frac{1}{50}\)
The slope of the road expressed as fraction is 2/100. When we simplify 2/100, the result obtained is 1/50
How to determine the slope in fractionFrom the question given above, we were told that the grade of the road is 2% which is equal to the slope. Thus, we can express 2% as fraction as illustrated below:
2% = 2/100
How to simplify 2/1002/100 can be simplified to it's lowest term as shown below:
2/100
Divide the numerator and denominator by 2
1/50
Thus,
2/100 = 1/50
Learn more about simplification of fractions:
https://brainly.com/question/16414484
#SPJ9
A moving company charges a flat rate of $150, and an additional $5 for each box. if a taxi service would charge no flat rate and $15 for each box, how many boxes would you need for it to be cheaper to use the moving company? (do not label your answer)
Answers
Answer:
16 boxes
Step-by-step explanation:
16x5=80+150=230>15x16=240
4h+1/2=2/3h need written into a verbal sentence
Answers
Answer:
four times "h" plus one-half is equal to two-thirds of "h".
\(h=-\frac{3}{20}\)
just in case u need it
Create an expression that has the same value as (6x-4) + (x + 5).
Write the correct numbers from the list in the blank boxes. Each number
may be used once, more than once, or not at all.
Answers
Answer: 7x + 1
Step-by-step explanation:
(6x-4)+(x+5)
Step 1: Remove Parentheses:
6x-4+x+5
Step 2: Combine Like Terms:
7x +1
Lainey is looking for a new apartment and her realtor keeps calling her with new listings. The calls only take a few minutes, but a few minutes here and there are really starting to add up. She's having trouble concentrating on her work. What should Lainey do? a) Tell her realtor she can only receive text messages O b) Limit the time spent on each call O c) Turn off her phone until she is on a break O di Call her realtor back when customers won't see her on the phone
Answers
a...cause she's having trouble concentrating,for her to work she needs to tell her realtor she can only receive text messages it enables her to know the process of the house hunt
QUESTION 1
Use the sine rule to find x. Rationalise and leave your answer in surd form; a+b√c
Use special angles where Sine 30 = and sine 45 = 2x-1 45 2x + 2 30
Answers
It can be seen that x = (3 ± √(9 + 32√3)) / 8, which can be expressed in surd form as (3 + √(9 + 32√3)) / 8 or (3 - √(9 + 32√3)) / 8.
How to solveTo find x using the sine rule, we need to solve the equation:
sine(45) / x = sine(30) / (2x + 2√3)
Simplifying this equation, we have:
(2x - 1) / x = 1 / (2x + 2√3)
Cross-multiplying and simplifying further, we get:
(2x - 1)(2x + 2√3) = x
Expanding the brackets, we have:
\(4x^2 + 4\sqrt3x - 2x - 2\sqrt3 = x\)
Rearranging the terms and simplifying, we get:
\(4x^2 - 3x - 2\sqrt3 = 0\)
Using the quadratic formula, we can solve for x:
x = (-(-3) ± √((-3)^2 - 4(4)(-2√3))) / (2(4))
x = (3 ± √(9 + 32√3)) / 8
Therefore, x = (3 ± √(9 + 32√3)) / 8, which can be expressed in surd form as (3 + √(9 + 32√3)) / 8 or (3 - √(9 + 32√3)) / 8.
Read more about sine rule here:
https://brainly.com/question/20839703
#SPJ1
The ratio of boys to girls Ms. Garcia’s class is 4:5.
a. If there are 12 boys in the class, how many girls are there?
Answers
Answer:
15 girls
4x3=12 so u multiply 3 on both sides and 5 x 3=15
In a survey, 16% of male college students said they lie sometimes to get a woman to go out on a date with them. If a male college student is chosen at random, find the probability that he does not lie to get a date with a woman
Answers
Answer:
84%
Step-by-step explanation:
if 16% is lying the opposite of that is 84% which is not lying
this means that 84% of the male college students do not lie
Use the method of undetermined coefficients to find one solution of
y′′−4y′+81y=48e^(2t)*cos(9t)+80e^(2t)*sin(9t)+3e^(−1t)
(It doesn't matter which specific solution you find for this problem.)
Answers
Using the method of undetermined coefficients, the particular solution is:
\(\mathrm{y_p(t) = 6e^{2t} \times cos(9t) + 3^{2t} \times sin(9t)}\)
How to find the particular solution?To use the method of undetermined coefficients, we assume that the particular solution has the same form as the forcing term, but with undetermined coefficients.
Let's start by finding a particular solution for the equation:
y′′ − 4y′ + 81y = 48\(e^{2t}\)cos(9t) + 80\(e^{2t}\)sin(9t) + 3\(e^{(-t)\)
Since the forcing term contains both exponential and trigonometric functions, we'll assume that the particular solution is of the form:
\(y_p\)(t) = A*\(e^{2t}\)cos(9t) + B\(e^{2t}\)*sin(9t) + C\(e^{(-t)\)
where A, B, and C are undetermined coefficients that we need to determine.
Let's find the first and second derivatives of \(y_p\)(t):
\(y'_p\)(t) = (2A + 9B)*\(e^{2t}\)*sin(9t) + (2B - 9A)*\(e^{2t}\)*cos(9t) - C\(e^{(-t)\)
\(y''_p\)(t) = (4A - 81B)*\(e^{2t}\)*cos(9t) + (4B + 81A)*\(e^{2t}\)*sin(9t) + C\(e^{(-t)\))
Substituting these expressions into the differential equation, we get:
(4A - 81B)*\(e^{2t}\)*cos(9t) + (4B + 81A)*\(e^{2t}\)*sin(9t) + C\(e^{(-t)\)
4[(2A + 9B)*\(e^{2t}\)*sin(9t) + (2B - 9A)*\(e^{2t}\)*cos(9t) - C\(e^{(-t)\)
81[A*\(e^{2t}\)cos(9t) + B\(e^{2t}\)*sin(9t) + C\(e^{(-t)\)]
= 48\(e^{2t}\)cos(9t) + 80\(e^{2t}\)sin(9t) + 3\(e^{(-t)\)
Simplifying and grouping terms, we get:
[(4A + 18B)cos(9t) + (18A - 4B)sin(9t)]\(e^{2t}\)+ (81C + 3)\(e^{(-t)\) = 48\(e^{2t}\)cos(9t) + 80\(e^{2t}\)sin(9t) + 3\(e^{(-t)\)
Since the two sides of the equation must be equal for all values of t, we can equate the coefficients of the exponential and trigonometric functions on both sides:
4A + 18B = 48 => A = 6
18A - 4B = 80 => B = 3
81C + 3 = 3 => C = 0
Therefore, the particular solution is:
\(y_p\)(t) = 6\(e^{2t}\)*cos(9t) + 3\(e^{2t}\)*sin(9t)
Thus, the general solution of the differential equation is:
\(\mathrm{y(t) = y_h(t) + y_p(t)}\)
where \(y_h\)(t) is the complementary solution. Since the characteristic equation of the differential equation is r² - 4r + 81 = 0, it has two complex conjugate roots: r = 2 ± 9i. Therefore, the complementary solution is:
\(y_h\)(t) = \(c_1\)*\(e^{2t}\)cos(9t) + \(c_2\)\(e^{2t}\)*sin(9t).
Learn more about particular solution
https://brainly.com/question/15127193
#SPJ1
brainliest and 20 points to whoever shows work the best

Answers
The missing part in the first triangle is 14
The missing part in the second triangle is 13.
What is the right triangle?The Pythagorean theorem is a fundamental theorem in geometry that applies specifically to right triangles.
According to Pythagorean theory, the square of the length of a right triangle's hypotenuse is equal to the sum of the squares of its legs.
For the first triangle as shown;
16^2 = 8^2 + t^2
t = √16^2 - 8^2
t = √192
t = 14
For the second triangle;
w= √8^2 + 10^2
w = 13
Learn more about right triangle:https://brainly.com/question/6322314
#SPJ1
Which of these equations has NO solution? A. 3 ( 2 x + 7 ) = 6 ( x + 4 ) − 3 B. 3 ( 6 x − 5 ) = 3 ( 6 x − 5 ) + x C. 8 ( x − 3 ) + 14 = 2 ( 4 x + 5 ) D. 13 x − 7 = 12 ( x − 1 ) + x + 5
Answers
Answer:
B ig
Step-by-step explanation:
A: 3(2x+7) = 6(X+4) - 3
<=> 6x+ 21 = 6x + 24 - 3 = 6x + 21
<=> 0 = 21 - 21 = 0
B: 3(6x-5)= 3(6x-5)+x
<=> 18x-15= 18x - 15 + x = 19x - 15
<=> 0 = x
C: 8(x-3) + 14= 2(4x+5)
<=> 8x - 24 + 14 = 8x - 10 = 8x + 10
<=> 0 = 0
D: 13x - 7 = 12( x - 1) +x + 5
<=> 13x - 7 = 12x -12 + x + 5 = 13x - 7
<=> 0 = 0
Absolute vale of x+2 if x is less than 2
Answers
Answer: The expression for the absolute value of x+2 when x is less than 2 is -(x+2).
Step-by-step explanation: When x is less than 2, x+2 is a negative number. The absolute value of a negative number is its opposite with the negative sign, so the absolute value of x+2 is -(x+2). Therefore, when x is less than 2, the expression for the absolute value of x+2 is -(x+2).
Find the amount (future value) of the ordinary annuity. (Round your answer to the nearest cent.)
$300/week for 9 1/2
years at 5.5%/year compounded weekly
Answers
Answer: $227,226.51
Step-by-step explanation:
First, we need to convert the period to weeks.
9 1/2 years = 9.5 years
1 year = 52 weeks
9.5 years = 494 weeks
Next, we can use the formula for the future value of an annuity:
FV = (PMT x (((1 + r/n)^(n*t)) - 1)) / (r/n)
where:
PMT = payment amount per period
r = annual interest rate
n = number of compounding periods per year
t = number of years
Plugging in the given values:
PMT = $300
r = 0.055 (5.5% expressed as a decimal)
n = 52 (compounded weekly)
t = 9.5 years = 494 weeks
FV = ($300 x (((1 + 0.055/52)^(52*494)) - 1)) / (0.055/52)
FV = $227,226.51
Therefore, the future value of the annuity is approximately $227,226.51.
What is the distance from C to B
please help me

Answers
Help pls I have no idea lol
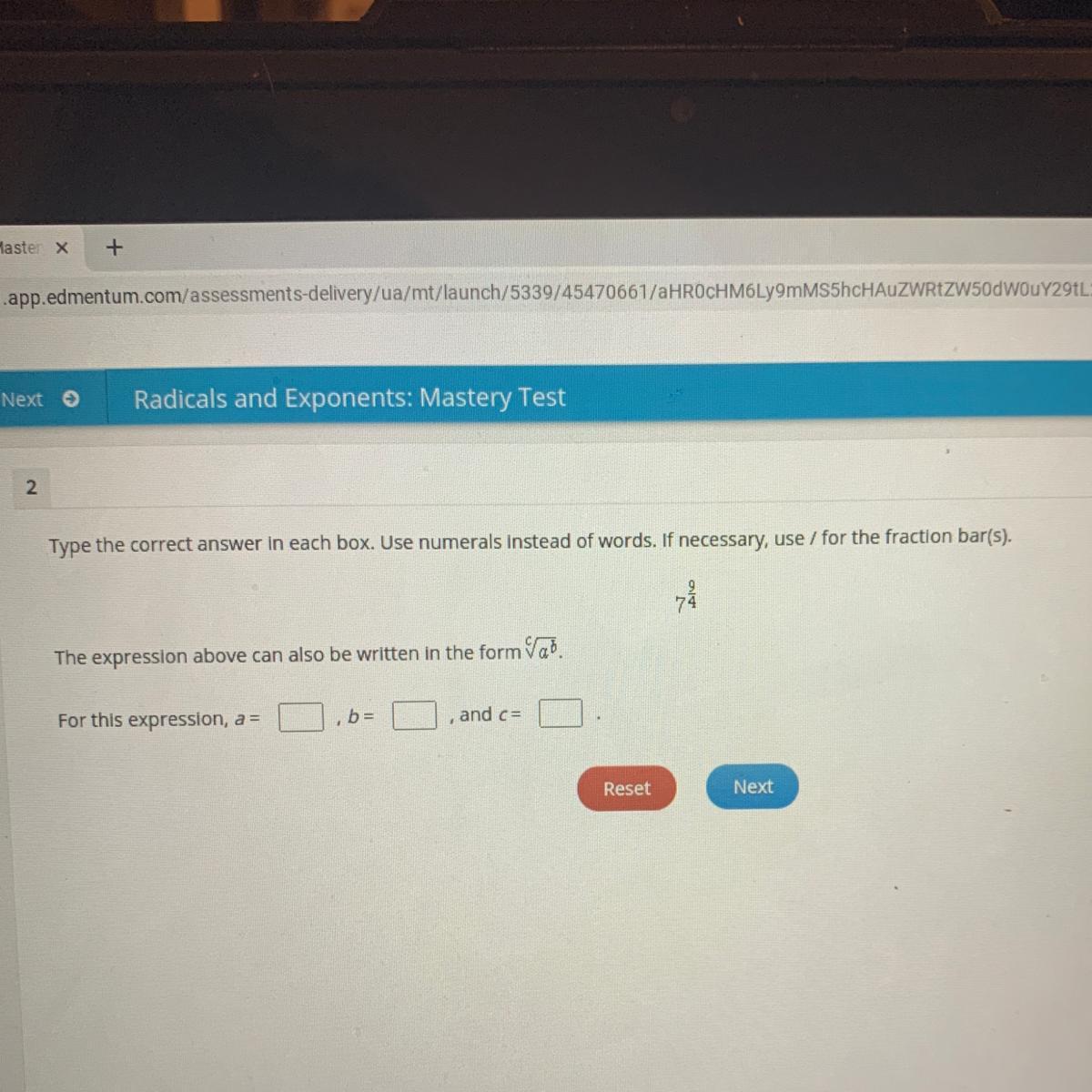
Answers
Answer:
a=7b=9c=4
Step-by-step explanation:
Write a paragraph proof of the Triangle Proportionality Theorem.
(Theorem 8.6)
__ __
Given: BD || AE
Prove: BA/CB = DE/CD

Answers
The Triangle Proportionality Theorem, also known as the Side Splitter Theorem, states that if a line is parallel to one side of a triangle, then it divides the other two sides proportionally.
Triangle Proportionality Theorem:
To prove this theorem, we begin by drawing a ΔABC with a line DE parallel to side AB. We then draw lines BD and CE, which intersect the parallel line DE at points F and G, respectively. By the properties of parallel lines, we know that ∠ADE and ∠ABD are congruent, and ∠AED and ∠ADB are congruent. Similarly, ∠CDE and ∠BDC are congruent, and ∠CED and ∠DCB are congruent.
We can then use the properties of similar triangles to show that ΔADE and ΔABC are similar, as are ΔCDE and ΔACB. This means that the ratios of corresponding side lengths are equal:
BA/DE = CA/CE and CB/DE = AB/BD
We can then substitute CA - BA for CB in the first equation, and BD for AB in the second equation:
BA/DE = (CA - BA)/CE and CB/DE = BD/(CA - BA)
Cross-multiplying both equations, we obtain:
BA * CE = DE * (CA - BA) and CB * DE = BD * (CA - BA)
Adding the two equations, we get:
BA * CE + CB * DE = (DE + CE) * CA
Dividing both sides by CB * DE, we obtain:
BA/CB = (DE + CE)/CE * CA/DE = DE/CD
Thus, we have proven the Triangle Proportionality Theorem.
To know more about Proportionality Theorem, visit:
https://brainly.com/question/29204751
#SPJ1
The shaded part of the model represents a fraction. Another fraction was subtracted from the first fraction.
Which expression is represented by the model?
1. 2/7 - 6/13
2. 13/21 - 2/7
3. 13/21 - 6/13
4. 6/13 - 2/7
Please help me with this question!
Answers
The expression represented by the model is 4. 6/13 - 2/7.
What is expression?Expression in math is a combination of numbers, symbols, and operators, such as variables and constants, used to represent a mathematical relationship. It can be used to represent the solution of a problem or the evaluation of a function. Expressions are used in algebra, calculus, and other branches of mathematics to describe the relationships between different elements.
This expression can be seen by looking at the model; the shaded portion represents the fraction 6/13 and the portion that was subtracted from it is 2/7. Thus, the expression represented by the model is 6/13 - 2/7.
To know more about expression click-
http://brainly.com/question/1859113
#SPJ1
(x)=4log(x+2) Which interval has the smallest average rate of change in the given function? 1≤x≤3 5≤x≤7 3≤x≤5 −1≤x≤1
Answers
Answer:
5≤x≤7
Step-by-step explanation:
For a given function f(x), the average rate of change in a given interval:
a ≤ x ≤ b
is given by:
\(r = \frac{f(b) - f(a)}{b - a}\)
Here we have:
f(x) = 4*log(x + 2)
And we want to see which interval has the smallest average rate of change, so we just need fo find the average rate of change for these 4 intervals.
1) 1≤x≤3
here we have:
\(r = \frac{f(3) - f(1)}{3 - 1} = \frac{4*log(3 + 2) - 4*log(1 + 2)}{2} = 0.44\)
2) 5≤x≤7
\(r = \frac{f(7) - f(5)}{7 - 5} = \frac{4*log(7 + 2) - 4*log(5 + 2)}{2} = 0.22\)
3) 3≤x≤5
\(r = \frac{f(5) - f(3)}{5 - 3} = \frac{4*log(5 + 2) - 4*log(3 + 2)}{2} = 0.29\)
4) −1≤x≤1
\(r = \frac{f(1) - f(-1)}{1 - (-1)} = \frac{4*log(1 + 2) - 4*log(-1 + 2)}{2} = 0.95\)
So we can see that the smalles average rate of change is in 5≤x≤7
Given AD = BC and AD parallel BC Prove ABCD is a parallelogram proof
Answers
Answer: the ABC is up illogic of the Paul Graham that makes the box square root to DC=BA
Step-by-step explanation:
Statements Reasons
1. AD ≅ BC; AD ∥ BC 1. given
2. ∠CAD and ∠ACB are alternate interior ∠s 2. definition of alternate interior angles
3. ∠CAD ≅ ∠ACB 3. alternate interior angles are congruent
4. AC ≅ AC 4. reflexive property
5. △CAD ≅ △ACB 5. SAS congruency theorem
6. AB ≅ CD 6. Corresponding Parts of Congruent triangles are Congruent (CPCTC)
7. ABCD is a parallelogram 7. parallelogram side theorem
on a larger map the coordinates for the location of another Washington DC landmark are eight and -10 in which quadrant of the map in this landmark located explain
Answers
The other Washington DC landmark with coordinates (8,-10) is located in the fourth quadrant of the map.
To determine in which quadrant of the map a point with coordinates (8,-10) is located, we need to look at the signs of the x and y coordinates.
Since the x-coordinate (8) is positive and the y-coordinate (-10) is negative, this point is located in the fourth quadrant.
In general, the four quadrants of a Cartesian coordinate system are divided by the x and y-axes.
The first quadrant is located in the upper right-hand corner and contains points with positive x and y coordinates.
The second quadrant is located in the upper left-hand corner and contains points with negative x and positive y coordinates.
The third quadrant is located in the lower left-hand corner and contains points with negative x and y coordinates.
Finally, the fourth quadrant is located in the lower right-hand corner and contains points with positive x and negative y coordinates.
To learn more about the coordinates;
https://brainly.com/question/27749090
#SPJ1
The surface area of a sphere is 900pi cubic cm. What is the length of its diameter.
Answers
The length of the diameter of the sphere is 30 cm.
The surface area of a sphere is given by the formula:
\(A = 4\pi r^2\)
where A is the surface area and r is the radius of the sphere.
We are given that the surface area of the sphere is 900π cubic cm. Therefore:
\(A = 4\pi r^2 = 900\pi\)
Dividing both sides by 4π, we get:
\(r^2 = 225\)
Taking the square root of both sides, we get:
r = 15
The diameter of the sphere is twice the radius, so:
d = 2r = 30
Therefore, the length of the diameter of the sphere is 30 cm.
for such more question on sphere
https://brainly.com/question/28228180
#SPJ11
Write 3 1/2 cups as a multiplication expression using the unit, 1 cup, as a factor.
I ABSOLUTELY NEED HELP BY TOMORROW!!! I AM GIVING 100 POINTS

Answers
3 1/2 cups can be expressed as the multiplication expression: 3 + 1/2.
How to Write 3 1/2 cups as a multiplication expression using the unit, 1 cup, as a factor.To express 3 1/2 cups as a multiplication expression using the unit "1 cup" as a factor, you can write it as:
3 1/2 cups = (3 + 1/2) cups = 3 cups + 1/2 cup
Since there are 1 cup in each term, we can rewrite it as:
3 cups + (1/2) cup
Now, we can express each term as a multiplication expression:
3 cups = 3 * 1 cup = 3
(1/2) cup = (1/2) * 1 cup = 1/2
Putting it all together, the multiplication expression is:
3 * 1 cup + (1/2) * 1 cup = 3 + 1/2
Therefore, 3 1/2 cups can be expressed as the multiplication expression: 3 + 1/2.
Learn more about expression at https://brainly.com/question/1859113
#SPJ1
