The probability that the interval estimation procedure will generate an interval that contains the actual value of the population parameter being estimated is the _____.
Answers
The population parameter being estimated is the confidence coefficient.
What is a confidence coefficient?The confidence coefficient is the confidence level stated as a proportion, rather than as a percentage. For example, if you had a confidence level of 99%, the confidence coefficient would be . 99. In general, the higher the coefficient, the more certain you are that your results are accurate.
probability is the likelihood that something will occur. When we don't know how an event will turn out, we can discuss the likelihood or likelihood of several outcomes. Statistics is the study of events that follow a probability distribution.
The area of mathematics known as probability deals with numerical representations of the likelihood that an event will occur or that a statement is true. An event's probability is a number between 0 and 1, where, roughly speaking, 0 denotes the event's impossibility and 1 denotes certainty.
Hence, The probability that the interval estimation procedure will generate an interval that does not contain the actual value of the population parameter being estimated is the confidence coefficient.
To learn more about the confidence coefficient from the given link:
https://brainly.com/question/28315730
#SPJ4
Related Questions
PLEASE HELP For the expression below, write two other equivalent expressions using different terms. Make sure one is fully simplified. -4(x+2)-2x+4
Answers
Given:
The given expression is
\(-4(x+2)-2x+4\)
To find:
The two other equivalent expressions.
Solution:
We have,
\(-4(x+2)-2x+4\)
Using distributive property, we get
\(=-4(x)-4(2)-2x+4\)
\(=-4x-8-2x+4\)
So, one equivalent expression is \(-4x-8-2x+4\).
On further simplification, we get
\(=(-4x-2x)+(-8+4)\)
\(=6x-4\)
Therefore, the second and fully simplified equivalent expression is \(6x-4\).
What is the effect on the graph of f(X) = |X| when the function is changed to
g(X) = -2|x|?
OA. The graph is reflected across the x-axis and stretched vertically by
a factor of 2.
O B. The graph is shifted to the left 2 units.
C. The graph is shifted down 2 units.
D. The graph is reflected across the x-axis and compressed vertically
by a factor of 2.
Answers
Answer:
A. The graph is reflected across the x-axis and stretched vertically by
a factor of 2.
Step-by-step explanation:
Transformations
For a > 0
\(f(x+a) \implies f(x) \: \textsf{translated $a$ units left}.\)
\(f(x-a) \implies f(x) \: \textsf{translated $a$ units right}.\)
\(f(x)+a \implies f(x) \: \textsf{translated $a$ units up}.\)
\(f(x)-a \implies f(x) \: \textsf{translated $a$ units down}.\)
\(a\:f(x) \implies f(x) \: \textsf{stretched parallel to the $y$-axis (vertically) by a factor of $a$}.\)
\(f(ax) \implies f(x) \: \textsf{stretched parallel to the $x$-axis (horizontally) by a factor of $\dfrac{1}{a}$}.\)
\(-f(x) \implies f(x) \: \textsf{reflected in the $x$-axis}.\)
\(f(-x) \implies f(x) \: \textsf{reflected in the $y$-axis}.\)
Given functions:
\(f(x)=|x|\)
\(g(x)=-2|x|\)
The series of transformations that take function f(x) to function g(x) are:
1. Reflection across the x-axis:
\(-f(x)\implies g(x)-|x|\)
2. Vertical stretch by a factor of 2:
\(-2f(x) \implies g(x)=-2|x|\)
what does what does this mean in math guys.?
Answers
Answer:
less than or equal to
Step-by-step explanation:
is used when a number cannot be bigger than a number, can be smaller or equal to
Answer:
Less than or equal to.
Step-by-step explanation:
So if I had 5 ≤ Z then Z is either the same thing as 5 or less than it.
what is the answer to
−1+8(−3+9)
Answers
Answer:42
Step-by-step explanation:
Od
33
Question 9 (1 point)
In the middle school PTA there is a total of 47 men and women. The number of women
in the PTA is 2 more than four times the number of men. How many women are in the
PTA?
a
42
38
ОООО
30
d
35
Answers
Answer:
38 women
Step-by-step explanation:
Question 9 (1 point)
In the middle school PTA there is a total of 47 men and women. The number of women the PTA is 2 more than four times the number of men. How many women are in the
PTA?
Let the number of men = x
Let the number of women = y
x + y = 47
y = 2 + 4x
We substitute
x + 2 + 4x = 47
Collect like terms
5x = 47 - 2
5x = 45
x = 45/5 = 9
y = 2 + 4x
y = 2 + 4 × 9
y = 2 + 36
y = 38
Therefore, the number of women = y = 38 women
f(x)= x^2-6x+5 Plot the x-intercept(s), y-intercept, vertex, and axis of symmetry for the function.
Answers
Step-by-step explanation:
The real part (red) and imaginary part (blue) of the Riemann zeta function along the critical line Re(s) = 1/2. The first non-trivial zeros can be seen at Im(s) = ±14.135, ±21.022 and ±25.011. The Riemann hypothesis, a famous conjecture, says that all non-trivial zeros of the zeta function lie along the critical line.
Plot the y intercept of y=3/2 x-2
Answers
Answer:
(0,-2)
Step-by-step explanation:
That point is the y intercept. (4/3,0) would be the x.
The linear density (mass per unit length) at a general location $(x, y, z)$ is a wire is given by the function $\rho(x, y, z)=|x+y|$. If the wire can be parametrioed as $r(\mathrm{w})=\sin w i+\cos u j+2 \mathrm{w} k$ with $u \in(0, \pi)$, then an expression for the mass of the wire is
$\int_0^\pi|\sin u+\cos u| \sqrt{1+4 u^2} \mathrm{~d} u$
$\int_0^\pi|\sin u+\cos u|(\cos u i-\sin u j+2 k) d u$
$\sqrt{5} \int_0^\pi|\sin u+\cos u| d u$
$\int_0^\pi(|\sin u| i+|\cos u| j) \cdot(\cos u \boldsymbol{i}-\sin u \boldsymbol{j}+2 k) d u$
$\int_0^\pi|\sin u+\cos u| d u$
Answers
The linear density (mass per unit length) at a general location $(x, y, z)$ is a wire is given by the function $\rho(x, y, z)=|x+y|$. If the wire can be parameterized as $r(w)=\sin wi+\cos uj+2wk$ with $u \in (0, \pi)$, then an expression for the mass of the wire is $\int_{0}^{\pi}|\sin u+\cos u| \sqrt{1+4u^2}du$.
The wire can be parameterized as follows:r(w)=sin(w)i+cos(u)j+2wkThe mass of an infinitesimal element of the wire is given by the formula
\[dM=\rho\sqrt{(dx)^{2}+(dy)^{2}+(dz)^{2}}\]
where \[\rho\] is the linear density of the wire and \[dx, dy, dz\] are differentials of the coordinate functions. Since the wire is parameterized
as \[r(w)=\sin wi+\cos uj+2wk\],
the differentials are as follows:
\[dr(w)=\frac{\partial r}{\partial w}dw
=\cos wi-\sin uj+2kdw\]The mass of the element of wire is, therefore, \[dM
=|x+y|\sqrt{(\cos w)^{2}+(\sin u)^{2}+4w^{2}}dw\]The mass of the entire wire is then given by the following integral: \[M
=\int_{0}^{\pi} |x+y|\sqrt{(\cos u)^{2}+(\sin u)^{2}+4w^{2}}du\] Substituting \[\sin u+\cos u
=r\cos(u-\alpha)\] where \[\alpha=\arctan(1)\], we get \[|x+y|
=\sqrt{2}|r\cos(u-\alpha)|=\sqrt{2}r|\cos(u-\alpha)|\]Substituting this into the integral for the mass and then factoring out \[\sqrt{2}\] gives\
[M=\sqrt{2}\int_{0}^{\pi} |\sin u+\cos u|\sqrt{(\cos u)^{2}+(\sin u)^{2}+4w^{2}}du\] Substituting \[\cos u=\frac{1}{\sqrt{5}}(\sqrt{2}\cos(\beta)+\sin(\beta))\] and \[\sin u=\frac{1}{\sqrt{5}}(\cos(\beta)-\sqrt{2}\sin(\beta))\] gives\[M=\sqrt{5}\int_{0}^{\pi} |\sin u+\cos u|du\] The absolute value sign can be removed since \[\sin u+\cos u>0\] for \[0
To know more about linear density visit:-
https://brainly.com/question/31388405
#SPJ`11
Which of the following hypothesis test statements below is a Type I Error?
a. Fail to reject the claim that community college students pay more than $1,250 per year on textbooks when the actual amount that community college students pay for textbooks is actually more than $1,250 per year.
b. Reject the claim that community college students pay at least $1,250 per year on textbooks when the actual amount that community college students pay for textbooks is actually at least $1,250 per year.
c. Fail to reject the claim that community college students pay at least $1,250 per year on textbooks when the actual amount that community college students pay for textbooks is actually less than $1,250 per year.
d. Reject the claim that community college students pay more than $1,250 per year on textbooks when the actual amount that community college students pay for textbooks is actually more than $1,250 per year.
Answers
The hypothesis test statement below is a Type I Error Failing to reject the claim that community college students pay at least $1,250 per year on textbooks when the actual amount that community college students pay for textbooks is actually less than $1,250 per year. Option C is the correct answer.
A Type I Error occurs when the null hypothesis is wrongly rejected, leading to the conclusion that there is a significant effect or difference when, in reality, there is no such effect or difference.
In this case, option c represents a Type I Error because it falsely fails to reject the claim of paying at least $1,250 per year on textbooks when the actual amount is less than $1,250.
Learn more about hypothesis tests at
https://brainly.com/question/17099835
#SPJ4
please help!!! brainliest answer will be marked!
Answers
2.50 + 5.50 =8
24/8 equals 6
6/2 equals 3
2.50(3) + 5.50(3) = 24.00
7.50 + 16.50 = 24.00
A delivery truck drives three routes in one day. The first route is 123 miles long, the second
route is 10 miles long, and the third route is 15 miles long.
What is the total number of miles the delivery truck drives?
Answers
To calculate the total number of miles the delivery truck drove, we add the lengths of the three routes together.
-> It drove 123 + 10 + 15 = 148 (miles).
the slope of the line through each pair of points 1) (-14,-7) , (5,-4)
Answers
M=3/19
This is right... this is our topic in math toooooooooo
Answer:
m=3/19
Step-by-step explanation:
Find the slope between 2 points:
(x1,y1)=(-14,-7)
(x2,y2)=(5,-4)
First you would use the slope Formula:
m= y2,-y1/x2,-x1
=-4--7/ 5--14
=3/19
1
2
cups of
3
Monica and Veronica are making strawberry pineapple smoothies. For every 1 cups of strawberries, they use
pineapple. Monica and Veronica have already put 1 cup of pineapple into the blender. The girls cannot agree how many
cups of strawberries to add to the blender to keep the same ratio, so they each did some work to determine the number
of cups of strawberries necessary for the smoothie.
(a)
Monica's Work:
3
13:
3- 3
a
ONU WOT
Veronica's Work
Answers
Answer:
For 1 cup of pineapple 1 .5 cups of strawberries are used.
Step-by-step explanation:
This question can be solved by using ratios
Strawberry : Pineapple
1 cup : 2/3 cup
x cup ; 1 cup
Using the cross product rule
2/3 * x= 1*1
x= 1*1 ÷ 2/3
x= 1*3/2= 1 1/2= 1.5
For 2 cups of pineapple 3 cups of strawberries are used.
For 1 cup of pineapple 1 .5 cups of strawberries are used.
For 3 cups of pineapple 4.5 cups of strawberries are used.
two tangents each intersect a circle at oppositea. endpoints of the same diameter. is it possible for the twob. tangents to intersect each other outside the c. circle? explain why or why not, using the information you d. learned in this lesson.
Answers
No, it is not possible for the two tangents to intersect each other outside the circle.
We have,
The concept used in this explanation is that a tangent to a circle is perpendicular to the radius at the point of tangency.
This is a fundamental property of circles and tangents, based on geometry and the definition of a tangent line.
No, it is not possible for the two tangents to intersect each other outside the circle.
This is because tangents to a circle are perpendicular to the radius at the point of tangency. If the tangents intersect with ed each other outside the circle, it would imply that they are not perpendicular to the radius, which contradicts the definition of a tangent.
Thus,
No, it is not possible for the two tangents to intersect each other outside the circle.
Learn more about Circle here:
https://brainly.com/question/11833983
#SPJ12
Yes, it is possible for the two tangents to intersect each other outside the circle only when the tangents are perpendicular to the diameter. They will intersect at the point directly opposite to the center of the circle. This concept combines the properties of tangents and circles that are normally covered in high school geometry.
Explanation:In the context Mathematics and Geometry, the situation you have described where two tangents to a circle meet at opposite ends of a diameter is indeed possible, but only in one specific scenario: when the tangents are perpendicular to the diameter and they intersect each other at the point directly opposite to the center of the circle. This is because, by geometry, a tangent to a circle is perpendicular to the radius at the point of tangency. Thus, if the tangents are drawn at the endpoints of a diameter, they will be parallel and will not intersect each other outside the circle.
In contrast, if the tangents are drawn such that they are perpendicular to the diameter, they will intersect at a point that is a distance from the center of the circle equivalent to the length of the radius, and directly opposite the center of the circle. This point of intersection of the tangents is outside the circle.
The properties of tangents and circles, which we use in the explanation, are part of the standard curriculum in high school geometry.
Learn more about Geometry here:https://brainly.com/question/31408211
#SPJ12
Omg I’m so confused about this pls
Answers
Answer: 1 is 50 and 2 is 70
Step-by-step explanation: these are both congruent and they are supplementary triangles
Because the triangles are just translated meaning they are moved and they are supplementary meaning they add up to 180° so we can subtract 180-70-60 to get 50 and the equation of triangle XYZ is 180-60-50 to get 70 those are the answers hope this helps :)
Draw the SFD and BMD for the following beam. Be sure to determine all key values, such as those at the supports and peak values.
Answers
Summary: The task is to draw the Shear Force Diagram (SFD) and Bending Moment Diagram (BMD) for a given beam, including the key values at the supports and peak values.
Explanation: To draw the SFD and BMD, we need to follow a systematic process. Firstly, we identify the support conditions of the beam and determine the reaction forces at each support. These reaction forces will be the key values at the supports. Next, we proceed to calculate the shear force and bending moment at various points along the beam, taking into account any point loads, distributed loads, or moments acting on the beam. These values will help us plot the SFD and BMD. At points where the shear force changes sign, there will be peak values in the BMD.
By accurately calculating and plotting the shear force and bending moment at each point, we can construct the SFD and BMD for the given beam, providing a visual representation of the internal forces and moments along the beam.
To know more about Bending Moment Diagram here: brainly.com/question/12950078
#SPJ11
what is 14.235 rounded to the nearest tenth
Answers
Write the equation of the function on the graph.
Answers
Answer:
\( \huge \boxed {y = |x| + 3}\)
Step-by-step explanation:
Similar to Parabola, except this is Modulus Function.
\( \boxed {y = a |x - h| + k} \\ a \: = slope \\ h = move \: \: to \: \: x - axis \\ k = move \: \: to \: \: y - axis\)
From the graph. The graph doesn't have any movement/transformation to x-axis, only y-axis. The graph only shifts up 3 units from y = |x|.
Both slopes are also 1 (from rise/run)
Hence, the answer is
\(y = |x| + 3\)
line b passes through points (-20, 4) and (-21, 96). line c is parallel to line b. what is the slope of line c?
Answers
The slope of the line c is - 92.
The points via which the line b passes are:
(-20, 4) and (-21, 96).
The slope of the line is given by:
m = (y₂ - y₁) / (x₂ - x₁)
Slope of the line b passing through these points are:
m = (96 - 4) / (- 21 + 20)
m = (92) / (-1)
m = - 92
Since, line b is parallel to line c,
Slope of line b = slope of line c
So, the slope of line c is also:
m' = - 92
Therefore, we get that, the slope of the line c is - 92.
Learn more about slope here:
https://brainly.com/question/3493733
#SPJ4
Solve: (5x - 3y + 2z)²
Answers
Answer:
25\(x^{2}\) - 30xy + 20xz + 9\(y^{2}\) - 12yz + 4\(z^{2}\)
Step-by-step explanation:
We multiply it out.
(5x - 3y + 2z) * (5x - 3y + 2z)
5x*5x + 5x*-3y + 5x*2z - 3y*5x - 3y*-3y -3y*2z + 2z*5x +2z * -3y +2z *2z
25\(x^{2}\) - 15xy + 10xz - 15xy + 9\(y^{2}\) - 6yz + 10xz - 6yz + 4\(z^{2}\)
Add like terms
25\(x^{2}\) - 15xy - 15xy + 10xz + 10xz + 9\(y^{2}\) - 6yz - 6yz + 4\(z^{2}\)
25\(x^{2}\) - 30xy + 20xz + 9\(y^{2}\) - 12yz + 4\(z^{2}\)
Find the vector v with the given magnitude and the same direction as u. Magnitude ||v|| = 20 Direction u = (-3, 4) V = (-16,12) X
Answers
The vector v with the given magnitude and the same direction as u. Magnitude ||v|| = 20 Direction u = (-3, 4) is 4
Given:
\(u = < -3, 4 >\)
Unit vector in the direction of u is
\(\hat{u}=\frac{u}{|u|}\)
Magnitude of vector u is
\(|u|=\sqrt{(-3)^2+(4)^2}=\sqrt{9+16}=\sqrt{25}=5\)
\(\hat{u}=\frac{1}{5} < -3,-4 >\)
Vector v with the magnitude |v|=20 and same direction as u is
\(v=|v|\hat{u} = > v=\frac{20}{5} =4\)
Therefore, the vector v with the given magnitude and the same direction as u. Magnitude ||v|| = 20 Direction u = (-3, 4) is 4.
Learn more about vector here:
https://brainly.com/question/15585996
#SPJ4
Tell whether the given value is a solution of the inequality
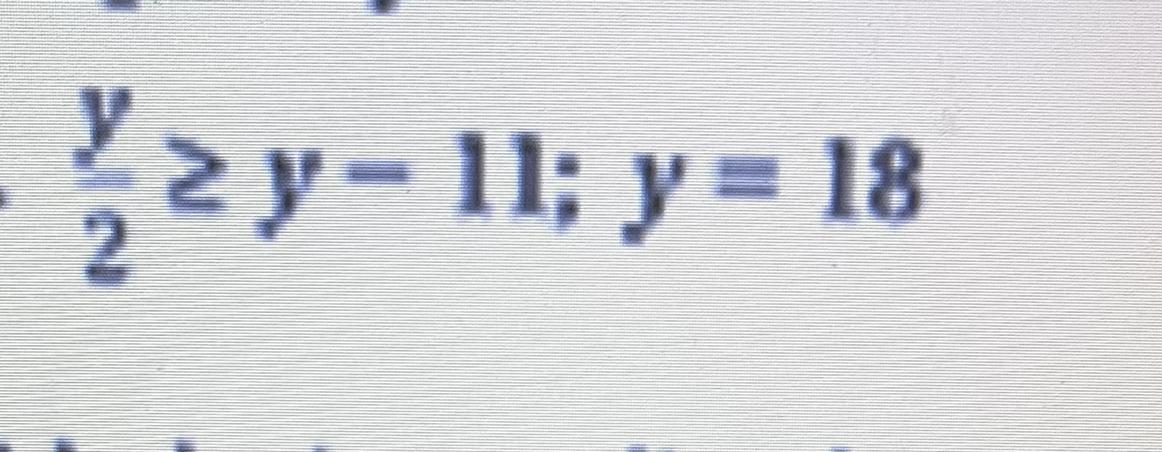
Answers
Answer:
Yes it is, because...
Step-by-step explanation:
This is an inequality, so you can treat it as an algebraic expression.
The first step is to multiple both sides by 2, to get rid of the 2 on the left side.
Your equation will now look like this:
y >= 2y - 22
The next step is to get all the y variables to one side, now that its a lot more simplified. Subtract 2y from both sides to get:
-y >= -22
Finally, cancel out the negative on both sides of the equation to get the y as a positive y, all by itself. This will get you:
y <= 22
REMINDER: when you divide by a negative number, such as in this case dividing by -1 on both sides, the inequality sign will flip!
y = 18 works because it is less than 22. (:
On a number line what number represents the point half the distance between A and B?
Answers
Answer:
A: -4
Step-by-step explanation:
Math.
Answer:
A. -4
Step-by-step explanation:
What expression is equivalent to: 4z x 2y
O 8 (z + y)
8zy
-8zy
O 8(xy)
Answers
Answer:
8 (z+y)
Step-by-step explanation:
Hope i helped you
In the fraction 7/8 , the Numerator Denominator is 7.
Answers
Answer:
The numerator
Step-by-step explanation:
numerator is the top
denominator is the bottom
a garden is to be laid out in a rectangular area and protected by a chicken wire fence. what is the largest possible area of the garden if only 100 running feet of chicken wire is available for the fence? round your answer to the nearest tenth, and use correct units.
Answers
Rounding to the nearest tenth, the largest possible area of the garden is 625 square feet.
What is area of rectangle?
The area of a rectangle is a measure of the region enclosed by its four sides. It represents the amount of space or surface covered by the rectangle. The formula to calculate the area of a rectangle is:
Area = Length × Width
To find the largest possible area of the garden given a limited amount of chicken wire fence, we need to determine the dimensions of the rectangular garden that would maximize its area.
Let's assume the length of the rectangular garden is L and the width is W. The perimeter of the garden, which is the length of the chicken wire fence required, can be expressed as:
Perimeter = 2L + 2W
Given that the perimeter is 100 running feet, we have:
2L + 2W = 100
Simplifying the equation, we get:
L + W = 50
To maximize the area, we need to maximize the product of the length and width, which represents the area of the garden:
Area = L * W
We can rewrite the equation for the area in terms of one variable using the constraint L + W = 50:
Area = (50 - W) * W
To find the maximum area, we can take the derivative of the area equation with respect to W, set it equal to zero, and solve for W:
d(Area)/dW = 50 - 2W = 0
2W = 50
W = 25
Substituting the value of W back into the equation L + W = 50:
L + 25 = 50
L = 25
Therefore, the largest possible area of the garden is obtained when the length and width are both 25 feet. The maximum area is:
Area = L * W = 25 * 25 = 625 square feet.
Rounding to the nearest tenth, the largest possible area of the garden is 625 square feet.
To learn more about area visit:
https://brainly.com/question/25292087
#SPJ4
will scale factor =12 enlarge, reduce or preserve
Answers
For {K} = 12, the image will remain preserved.
What is image dilation?An enlargement or reduction of a figure that preserves shape but not size.All dilations are similar to the original figure.Dilations have a center and a scale factor.Given is the scale factor of {K} = 12.
We can write the scale factor as -
reduction {for K < 1}
enlargement {for K > 1}
preserved {for K = 1}
For {K} = 12, the image will remain preserved.
Therefore, for {K} = 12, the image will remain preserved.
To solve more questions on dilation, visit the link below -
brainly.com/question/2859427
#SPJ9
Prove that if 5(m - 1) = -25, then m = -4.
Answers
Answer:
The equation is true
Step-by-step explanation:
First, input -4 instead of m in the equation:
5(-4 - 1) = -25
Then, distribute:
-20 - 5 = -25
Finally, simplify:
-25 = -25
This equation is true, and that's how you prove it.
Hope this helps!
Answer:
M= -4
Step-by-step explanation:
1. Distribute the 5 into the parentheses
5m-5=-25
2. Now add 5 on both sides
5m=-20
3. Now divide 5 by -20
m=-4
Are the ratios 3:6 and 1:9 equivalent?
Answers
Answer:
no they are not equivalent
Step-by-step explanation:
Answer:
No
Step-by-step explanation:
The ratio would have to be 1:2 or 6:12 or with other factors of the two numbers but the numbers have to be multiplied or divided by the same number to get to those factors in order for them to remain equivalent.
For example: If you were to multiply the 3 by 2 but the 6 by three you'd get 6:18 which simplified is 3:9 not 3:6 but if you multiply both the 3 and the 6 by 3 you'd get 9:18 with can by simplified to 3:6
decrease 40 by 62 1/2%
Answers
Answer:
15
Step-by-step explanation:
Take 62.5 from 100 = 37.5
divide this by 100 = 0.375
times 40 by this
0.375 x 40 = 15