the quotient of 9 3/4 and 5/8
Answers
Answer:
15.6
Step-by-step explanation:
The answer is 15.6 because if you divide 9 3/4 by 5/8, you get 78/5, or 15.6 in decimal form. Hope it helps!
Related Questions
If f(x) = 2x+ 1, then f(3) =
i cant really seem to understand how to work it out.
Answers
Answer:
f(3) = 7
Step-by-step explanation:
f(x) = 2x + 1
f(3) = 2(3) + 1
f(3) = 6 + 1
Substitute the 3 in for x.
f(3) means that x is equal to 3.
This just means we substitute the value of 3 into the f(x) = 2x+ 1 to get
f(x) = 2(3)+ 1,
f(3) = 2(3)+ 1,
f(3) = 6+ 1,
f(3) = 7
Can someone help with this please?

Answers
Answer:
1 is linear, 2 is linear, 3 is not linear, 4 is not linear
Answer:
Function 1 is linear
Function 2 is linear
Function 3 is not linear
Function 4 is not linear
please help
there are 2 possible answers
Let x be the number of boys in a class and y be the number of girls. Which equation represents 2 boys for
every 5 girls? Select all that apply.
Answers
Answer:
this is not an answer but I will post one, could you tell us what the answer choices are?
Step-by-step explanation:
it would help with the answers.
Determine the equation of the line shown in the graph:

Answers
Answer:
x=3
Line passes through 3 on the x-axis.
Tanya is given the graphs of the following functions. The functions Latex: f(x) f ( x ) and Latex: g(x) g ( x ) are linear, and the function Latex: s(x) s ( x ) is quadratic. f ( x ) = 3 x − 8 g ( x ) = − 2 x + 5 s ( x ) = 4 x 2 − 9 x + 2 Tanya is then asked to find the graph of Latex: (f\cdot g)(x) ( f ⋅ g ) ( x ) and the graph of Latex: (g\cdot s)(x)\textsf{.} For each combined function, she is given four options to choose from. What clues will help Tanya identify the correct graph of Latex: (f\cdot g)(x)\textsf{?} What clues will help Tanya identify the correct graph of Latex: (g\cdot s)(x)\textsf{?}
Answers
The functions (f.g)(x) and (g.s)(x) are illustrations of composite function
The values of the composite functions are:
(fg)(x) = -6x^2 + 31x - 40 and (gs)(x) = -8x^3 + 38x^2 -49x+ 10
How to determine the equation of the composite functionThe equation of the functions are given as:
f(x) = 3x - 8
g(x) = -2x + 5
s(x) = 4x^2 - 9x + 2
.
The composite functions are calculated using:
(fg)(x) = f(x) * g(x)
So, we have:
(f g)(x) = (3x - 8) * (-2x + 5)
Evaluate the product
(fg)(x) = -6x^2 + 15x + 16x - 40
Evaluate the like terms
(fg)(x) = -6x^2 + 31x - 40
Also, we have:
(gs)(x) = g(x) * s(x)
So, we have:
(gs)(x) = (-2x + 5) * (4x^2 - 9x + 2)
Expand
(gs)(x) = -8x^3 + 18x^2 -4x + 20x^2 - 45x + 10
Collect like terms
(gs)(x) = -8x^3 + 18x^2 + 20x^2-4x - 45x + 10
Evaluate the like terms
(gs)(x) = -8x^3 + 38x^2 -49x+ 10
Hence, the values of the composite functions are:
(fg)(x) = -6x^2 + 31x - 40 and (gs)(x) = -8x^3 + 38x^2 -49x+ 10
Read more about composite functions at:
https://brainly.com/question/10687170
Sandra currently earns $30 per hour at her work. Her boss has decided to
eive her a 15% raise. What is Sandra's new hourly wage?
Answers
30 × 0.15 = 4.5
30 + 4.5 = 34.5
Sandra's new wage is $34.5 per hour.
Find the area of the figure. Round to the nearest hundredth where necessary.
35 in
37 in

Answers
Answer:
Area = 996 in^2
Step-by-step explanation:
First, look at the triangle on top, well, like half of it. You can use Pythagorean theorem to find the missing side. See image. Double it to find the base of the whole triangle. Use Area of a triangle:
= 1/2 b•h
to find the area of the top (the triangle).
The 24, used for the triangle base is also the side length of the square below. See image.
Area of a square is:
Area = s^2
OR, just l×w or b×h,
all the same.
Add together the triangle area and the square's area for the final answer. See image.

Use <,>, or = to compare the value.
0.4______ 1/4
Answers
Answer:
>
Step-by-step explanation:
Answer: >
Step-by-step explanation: Because 1/4 as a decimal is .25 and you can change the 0.4 to 0.40; they are the same thing. And .40 is greater than .25
PLEASE HELP MEEEEEEEEEEEEEEEEEEEEEE
There are 360 people in a movie theater. Of these people, 35% bought student tickets, and 45% bought adult tickets. The rest bought senior-citizen tickets. how many people bought senior tickets?
Answers
45+35=80
100-80=20
360×20/100
72 so the answer is this and the formula E=T×%/100
Total Marks
Total Questions
Attempted Questions
Dale Alpiou
ning
Q2 Which statement is true?
All squares are rhombi.
All rectangles are rhombi.
All parallelograms are rectangles.
All trapezoids are parallelograms.
Answers
Answer:
All parallelograms are rectangles.
22) A game is played using one die. If the die is rolled and shows a 2, the player wins $8. If the die
shows any number other than 2, the player wins nothing. If there is a charge of $1 to play the
game, what is the game's expected value?
A) $0.33
B) $7.00
C)-$0.33
D) -$1
Answers
The game's expected value is (A) $0.33
How to determine the expected amount the player wins or lose?From the question, we have the following parameters that can be used in our computation:
Outcome of 2 = Win $8
Other outcomes = Win $0
A die has the following sample space
S = {1, 2, 3, 4, 5, 6}
Using the above sample space, the individual probabilities are:
P(Outcome of 2) = 1/6
P(Others) = 5/6
The expected value is calculated as
Expected value = Sum of the products of the probability and the amount win/lose
So, we have
Expected = 1/6 * 8 + 5/6 * 0
Evaluate the products
Expected = 1.33
The charge is $1
So, we have
Expected = 1.33 - 1
Evaluate
Expected = 0.33
Hence, the expected amount is $0.33
Read more about expected values at
brainly.com/question/15858152
#SPJ1
What is A−1? Enter your answer by filling in the boxes. Enter any fractions as simplified fractions.

Answers
Step-by-step explanation:
ooo matrics um if you give me a second ill solve it
Help Will give Branliest

Answers
2n + 5 - 6 = 5
Please help me
Answers
Answer:
n = 3
Step-by-step explanation:
2n+5-6 = 5 ( add 6 on both sides)
2n+5=11 (then subtract 5 on both sides)
2n=6 (Then divide by 2 on both sides)
n = 3
Answer:
\(n=3\)
Step-by-step explanation:
\(2n + 5 - 6 = 5\)
Subtract 5 from both sides:
\(2n+5-6-5=5-5\)
\(2n-6=0\)
Add 6 to both sides:
\(2n-6+6=0+6\)
\(2n=6\)
Divide both sides by 2:
\(\frac{2n}{2}=\frac{6}{2}\)
\(n=3\)
OAmalOHopeO
do anyone know the answer?

Answers
Answer:
C.
Step-by-step explanation:
To find which table is correct, you first have to plot the graph. First, pick some easy points on the X axis to graph. Some of these points could be -4, 0 and 4. Now you need to fill in the equation.
Y = -1/2*-4 - 2 = 0
Y = -1/2*0 - 2 = -2
Y = -1/2*4 - 2 = -4
Now you can plot the points and draw your line. Once you have done this, you check each table and see if all the points match up. Doing so would give you answer C.
Also the graph from the equation can be seen below

Please use the following for the next 6 questions. Suppose that the average weekly earnings for employees in general automotive repair shops is $450, and that the population standard deviation for the earnings for such employees is $50. A sample of 100 such employees is selected at random.
1) What is the probability distribution of the average weekly earnings for employees in general automotive repair shops?
2) Find the probability that the average weekly earnings is less than $445.
3) Find the probability that the average weekly earnings is exactly equal to $445.
4) Find the probability that the average weekly earnings is between $445 and $455.
5) In answering the previous 3 questions, did you have to make any assumptions about the population distribution?
6) Now assume that the weekly earnings for employees in all general automotive repair shops is normally distributed, obtain the probability that a given employee will earn more than $480 in a given week.
Answers
1) The probability distribution of the average weekly earnings for employees in general automotive repair shops is the sampling distribution of the sample mean. According to the Central Limit Theorem, if the sample size is large enough, the sampling distribution of the sample mean is approximately normal, with a mean equal to the population mean and a standard deviation equal to the population standard deviation divided by the square root of the sample size.
2) To find the probability that the average weekly earnings is less than $445, we can standardize the sample mean and use a z-table. The z-score for $445 is calculated as follows: z = (445 - 450) / (50 / sqrt(100)) = -1. Using a z-table, we find that the probability that the average weekly earnings is less than $445 is approximately 0.1587.
3) Since we are dealing with a continuous distribution, the probability that the average weekly earnings is exactly equal to any specific value is zero.
4) To find the probability that the average weekly earnings is between $445 and $455, we can subtract the probability that it is less than $445 from the probability that it is less than $455. The z-score for $455 is calculated as follows: z = (455 - 450) / (50 / sqrt(100)) = 1. Using a z-table, we find that the probability that the average weekly earnings is less than $455 is approximately 0.8413. Therefore, the probability that it is between $445 and $455 is approximately 0.8413 - 0.1587 = 0.6826.
5) In answering questions 2-4, we made an assumption about the population distribution based on the Central Limit Theorem. We assumed that since our sample size was large enough (n=100), our sampling distribution would be approximately normal.
6) If we assume that weekly earnings for employees in all general automotive repair shops are normally distributed with a mean of $450 and a standard deviation of $50, then we can calculate the z-score for an employee earning more than $480 in a given week as follows: z = (480 - 450) / 50 = 0.6. Using a z-table, we find that the probability that an employee will earn more than $480 in a given week is approximately 1 - 0.7257 = 0.2743.
3 divided by 3/4 bag raisem
Answers
The simplification of the given expression above after division would be = 4
How to simplify the given expression?
When a fraction is to be divided by a whole number, a multiplication sign can be used whereby the numerator becomes the denominator and the denominator becomes the numerator.
That is, 3 ÷ 3/4
= 3 × 4/3
= 4
Learn more about division here:
https://brainly.com/question/25289437
#SPJ1
Please help me please
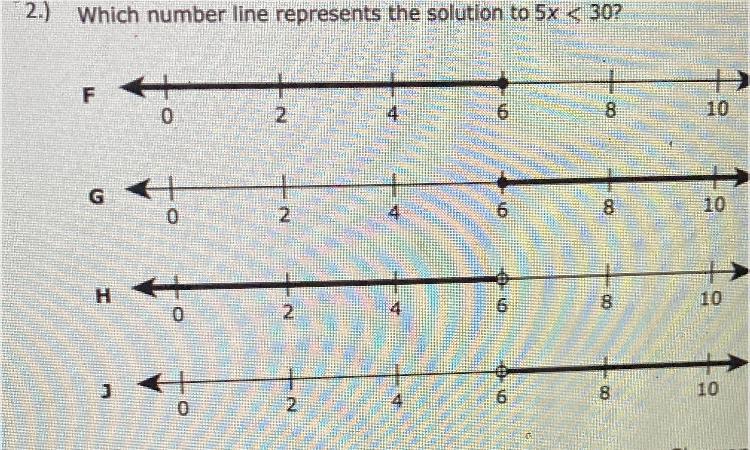
Answers
Answer:
5x<30
Open circle.
5x<30
Divide by 5
x < 6
Open circle, arrow to the left. Answer is H
A popular charity used 31% of its donations on expenses. An organizer for a rival charity wanted to quickly provide a donor with evidence that the popular charity has expenses that are higher than other similar charities. The organizer randomly selected 10 similar charities and examined their donations. The percentage of the expenses that those 10 charities spend on expenses is given below. Use a TI-83, TI-83 Plus, or TI-84 calculator to test whether the mean is less than 31% and then draw a conclusion in the context of the problem. Use α=0.05. 26 12 35 19 25 31 18 35 11 26 Select the correct answer below: Reject the null hypothesis. There is sufficient evidence to conclude that the mean is less than 31%. Reject the null hypothesis. There is insufficient evidence to conclude that the mean is less than 31%. Fail to reject the null hypothesis. There is sufficient evidence to conclude that the mean is less than 31%. Fail to reject the null hypothesis. There is insufficient evidence to conclude that the mean is less than 31%.
Answers
Answer:
Reject the null hypothesis. There is sufficient evidence to conclude that the mean is less than 31%.
Step-by-step explanation:
In this case we need to test whether the popular charity has expenses that are higher than other similar charities.
The hypothesis for the test can be defined as follows:
H₀: The popular charity has expenses that are higher than other similar charities, i.e. μ > 0.31.
Hₐ: The popular charity has expenses that are less than other similar charities, i.e. μ < 0.31.
As the population standard deviation is not known we will use a t-test for single mean.
Compute the sample mean and standard deviation as follows:
\(\bar x=\frac{1}{n}\sum X=\frac{1}{10}\cdot[0.26+0.12+...+0.26]=0.238\\\\s= \sqrt{ \frac{ \sum{\left(x_i - \overline{X}\right)^2 }}{n-1} } = \sqrt{ \frac{ 0.0674 }{ 10 - 1} } =0.08654\approx 0.087\)
Compute the test statistic value as follows:
\(t=\frac{\bar x-\mu}{s/\sqrt{n}}=\frac{0.238-0.31}{0.087/\sqrt{10}}=-2.62\)
Thus, the test statistic value is -2.62.
Compute the p-value of the test as follows:
\(p-value=P(t_{\alpha, (n-1)}<-2.62}\)
\(=P(t_{0.05,9}<-2.62)\\=0.014\)
*Use a t-table.
Thus, the p-value of the test is 0.014.
Decision rule:
If the p-value of the test is less than the significance level then the null hypothesis will be rejected and vice-versa.
p-value = 0.014 < α = 0.05
The null hypothesis will be rejected at 5% level of significance.
Thus, concluding that there is sufficient evidence to conclude that the mean is less than 31%.
Question 5 (1 point)
The perimeter of a rectangular patio is 80 feet. The length is 4 feet greater than the
width. What is the width, in feet, of the patio?
Answers
Answer:
18 feet
Step-by-step explanation:
Perimeter=2(l+b)
80=2(w+w+4)
80=2(2w+4)
80=4w+8
80-8=4w
72/4=w
W=18 feet
explanation :
x^2+6x+8÷x^2-16 simplify
Answers
Answer:
The answer is in the file below, I wasn't able to make it in text form.

The numbers of customers that visited a store each hour for several hours after the store opened at 8 am are shown in the table. Hours after 8 am 1 3 4 6 9 Number of Customers 2 15 18 13 0 Which statement best describes the data?
Answers
The statement which best describes the data given is C) The data can be modeled by a quadratic function.
Given a data,
The numbers of customers that visited a store each hour for several hours after the store opened at 8 am are shown in the table.
It is clear that the number of customers increases to 18 for the first 4 hours and then decreases to 0 after 9 hours.
So this data cannot be modeled by a linear function or an exponential function.
Also since the number of customers arriving is not constant, this cannot be expressed as constant function.
So it is quadratic function.
Hence the correct option is c.
Learn more about Quadratic Functions here :
https://brainly.com/question/18958913
#SPJ1
Samantha usually makes lemonade with 8 cups of water and 3/4 cup of sugar. For today's picnic, she wants to make 28 cups of lemonade. How much sugar does she need? Show all of your work.
Answers
Answer:
21 cups of sugar
Step-by-step explanation:
3/4 x 28 = 21
What is the approximate area of a circle with radius 6 cm?

Answers
Answer:
133 m^2
Step-by-step explanation:
to find are of a circle it’s r^2 times pi
6^2 x pi
36 pi
113 m^2
Hopes this helps please mark brainliest
Answer:
Answer C is correct
Step-by-step explanation:
The formula to find the area of a circle is:
A = πr²
Here,
r => radius = 6m
Let us find the area of the circle.
A = πr²
A = 3.14 × 6 × 6
A = 113.04 m²
Approx. = 113m²
There is a number that is three-fifths the total of the other number. When four is added to one of the numbers their sum will be equal to the other number. There are two pairs of numbers that satisfy these descriptions. What are they?
Answers
Answer:
-10, -6
6, 10
Step-by-step explanation:
Let the one number be x.
One number is 3/5 of the other number.
The numbers are x and 3x/5.
Add 4 to one number, the sum equals the other number.
There are two possibilities.
A) x + 4 = 3x/5
B) 3x/5 + 4 = x
Solve A)
5x + 20 = 3x
2x = -20
x = -10
Solve B)
3x + 20 = 5x
2x = 20
x = 10
According to A)
x = -10
3x/5 = -6
According to B)
x = 10
3x/5 = 6
Answer:
-10, -6
6, 10
If the area of a square inscribed in a circle is
25, what is the area of the circle?
Answers
The area of a square inscribed in a circle is 25, then the area of the circle is 25π/2 or approximately 39.27 square units.
To solve this problem, we can use the relationship between the area of a square inscribed in a circle and the area of the circle itself.
When a square is inscribed in a circle, the diagonal of the square is equal to the diameter of the circle. Let's assume that the side length of the square is 's' and the radius of the circle is 'r'.
We are given that the area of the square is 25, so we can find the side length of the square:
Area of square = \(s^2 = 25\)
Taking the square root of both sides, we get:
s = √25 = 5
Since the diagonal of the square is equal to the diameter of the circle, we can find the diameter of the circle:
Diagonal = Diameter = s√2 = 5√2
The radius of the circle is half the diameter, so:
Radius = 5√2 / 2 = (5√2)/2
Now, we can calculate the area of the circle using the formula:
Area of circle = \(\pi r^2\)
Substituting the value of the radius, we get:
Area of circle = π((5√2)/\(2)^2\) = π(25/2) = 25π/2
Therefore, the area of the circle is 25π/2 or approximately 39.27 square units.
For more question on square visit:
https://brainly.com/question/428672
#SPJ8
Rockwell hardness of pins of a certain type is known to have a mean value of 50 and a standard deviation of 1.2.a. If the distribution is normal, what is the probability that the sample mean hardness for a random sample of 9 pins is at least 51?b. Without assuming population normality, what is the (approximate) probability that the sample mean hardness for a random sample of 40 pins is at least 51?
Answers
Answer:
a
\(P(\= X \ge 51 ) =0.0062\)
b
\(P(\= X \ge 51 ) = 0\)
Step-by-step explanation:
From the question we are told that
The mean value is \(\mu = 50\)
The standard deviation is \(\sigma = 1.2\)
Considering question a
The sample size is n = 9
Generally the standard error of the mean is mathematically represented as
\(\sigma_x = \frac{\sigma }{\sqrt{n} }\)
=> \(\sigma_x = \frac{ 1.2 }{\sqrt{9} }\)
=> \(\sigma_x = 0.4\)
Generally the probability that the sample mean hardness for a random sample of 9 pins is at least 51 is mathematically represented as
\(P(\= X \ge 51 ) = P( \frac{\= X - \mu }{\sigma_{x}} \ge \frac{51 - 50 }{0.4 } )\)
\(\frac{\= X -\mu}{\sigma } = Z (The \ standardized \ value\ of \ \= X )\)
\(P(\= X \ge 51 ) = P( Z \ge 2.5 )\)
=> \(P(\= X \ge 51 ) =1- P( Z < 2.5 )\)
From the z table the area under the normal curve to the left corresponding to 2.5 is
\(P( Z < 2.5 ) = 0.99379\)
=> \(P(\= X \ge 51 ) =1-0.99379\)
=> \(P(\= X \ge 51 ) =0.0062\)
Considering question b
The sample size is n = 40
Generally the standard error of the mean is mathematically represented as
\(\sigma_x = \frac{\sigma }{\sqrt{n} }\)
=> \(\sigma_x = \frac{ 1.2 }{\sqrt{40} }\)
=> \(\sigma_x = 0.1897\)
Generally the (approximate) probability that the sample mean hardness for a random sample of 40 pins is at least 51 is mathematically represented as
\(P(\= X \ge 51 ) = P( \frac{\= X - \mu }{\sigma_x} \ge \frac{51 - 50 }{0.1897 } )\)
=> \(P(\= X \ge 51 ) = P(Z \ge 5.2715 )\)
=> \(P(\= X \ge 51 ) = 1- P(Z < 5.2715 )\)
From the z table the area under the normal curve to the left corresponding to 5.2715 and
=> \(P(Z < 5.2715 ) = 1\)
So
\(P(\= X \ge 51 ) = 1- 1\)
=> \(P(\= X \ge 51 ) = 0\)
Using the normal distribution and the central limit theorem, we have that there is a:
a) 0.0062 = 0.62% probability that the sample mean hardness for a random sample of 9 pins is at least 51.
b) 0% approximate probability that the sample mean hardness for a random sample of 40 pins is at least 51.
In a normal distribution with mean and standard deviation , the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
It measures how many standard deviations the measure is from the mean. After finding the z-score, we look at the z-score table and find the p-value associated with this z-score, which is the percentile of X. By the Central Limit Theorem, the sampling distribution of sample means of size n has standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).In this problem:
Mean of 50, hence \(\mu = 50\)Standard deviation of 1.2, hence \(\sigma = 1.2\)Sample of 9, hence \(n = 9, s = \frac{1.2}{\sqrt{9}} = 0.4\).Item a:
The probability is 1 subtracted by the p-value of Z when X = 51, hence:
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{51 - 50}{0.4}\)
\(Z = 2.5\)
\(Z = 2.5\) has a p-value of 0.9938.
1 - 0.9938 = 0.0062
There is a 0.0062 = 0.62% probability that the sample mean hardness for a random sample of 9 pins is at least 51.
Item b:
Even though the distribution is not normal, the sample size is of \(n = 40 > 30\), hence the Central Limit Theorem can be applied.
\(s = \frac{1.2}{\sqrt{40}} = 0.19\)
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{51 - 50}{0.19}\)
\(Z = 5.26\)
\(Z = 5.26\) has a p-value of 1.
1 - 1 = 0
0% approximate probability that the sample mean hardness for a random sample of 40 pins is at least 51.
A similar problem is given at https://brainly.com/question/24663213
PLEASE HELP WITH THIS! PLEASE! SURFACE AREA. I HAVE NO CLUE!!

Answers
Answer: 626 yd^2
Step-by-step explanation: First you need to split the figure into 2 rectangular prisms (see attached image). The tallest rectangular prism has a length of 12 yd, a width of 3 yd, and a height of 11 yd. The shorter one has a length of 12yd, a width of 4 yd, and a height of 4 yd. The surface area equation is SA=2(wl+hl+hw). First solve for the taller rectangular prism. SA=2(3x12+11x12+11x3). SA=2(36+132+33). SA=2(201). SA=402 yd^2. Now solve for the smaller rectangular prism. SA=2(4x12+4x12+4x4). SA=2(48+48+16). SA=2(112). SA=224 yd^2. Lastly, add both values together. 402+224=626 yd^2.

PLEASE HELP ASAP
NO LINKS PLEASE

Answers
Answer:
A linear relationship (or linear association) is a statistical term used to describe a straight-line relationship between two variables. Linear relationships can be expressed either in a graphical format or as a mathematical equation of the form y = mx + b.
Step-by-step explanation:I hope it helps
which of the following graphs could describe the system of equations
a) blue
b)purple
c)green
d)pink

Answers
Answer:
It is purple
Step-by-step explanation:
Answer:
purple
because they interset each other
Step-by-step explanation: