The radius of a circle is 7 kilometers. What is the length of a 90° arc?
Answers
Find the length of the circumference:
Circumference = 2 x pi x radius
Circumference = 2 x 3.14 x 7
Circumference = 43.96 kilometers
90 degrees is 1/4 of a circle ( 360/4 = 90)
Arc length = 43.96/4 = 10.99 kilometers
(Round answer as needed)
Answer:
Step-by-step explanation:
Related Questions
A ladder 13 meters long rests on horizontal ground and leans against a vertical wall. The bottom of the ladder is pulled away from the wall at the rate of 0.6 m/sec. a) Find the rate at which the top of the ladder is sliding down the wall when the bottom of the ladder is 5 m from the wall. b) Find the rate of change of the angle between the ground and the ladder when the bottom of the ladder is 5 m from the wall. c) Find the rate of change of the area of the triangle bounded by the ladder, the building, and ground, when the bottom of the ladder is 5 m from the wall.
Answers
a) The rate at which the top of the ladder is sliding down the wall when the bottom of the ladder is 5 m from the wall is -0.1 m/s.
b) The rate of change of the angle between the ground and the ladder when the bottom of the ladder is 5 m from the wall is -25/676 rad/s.
c) The rate of change of the area of the triangle bounded by the ladder, the building, and the ground, when the bottom of the ladder is 5 m from the wall is 3.5 m^2/s.
a) To find the rate at which the top of the ladder is sliding down the wall, we start by expressing the length of the ladder, z, in terms of the distances x and y using the equation z^2 = x^2 + y^2.
By differentiating this equation with respect to time, we obtain 2z(dz/dt) = 2x(dx/dt) + 2y(dy/dt), where dz/dt represents the rate of change of z, dx/dt is the rate at which x is changing, and dy/dt is the rate at which y is changing.
Given that dx/dt = 0.6 m/s, x = 5 m, and z = 13 m, we can substitute these values into the equation and simplify to find 13(dz/dt) = 3 + y(dy/dt).
To isolate dy/dt, we differentiate equation (1) with respect to t, resulting in dy/dt = [2z(dz/dt) - 2x(dx/dt)] / (2y).
Substituting the given values and dz/dt = 0.6, we find dy/dt = (13/12)(dz/dt) - (1/2). Plugging in dz/dt = 0.6, we obtain dy/dt = (13/12) * 0.6 - 0.5 = -0.1 m/s. The negative sign indicates that the top of the ladder is sliding down the wall.
b)
This can be determined by differentiating the equation involving the tangent of the angle and applying the chain rule.
To find the rate of change of the angle, θ, between the ground and the ladder, we start with the equation tan θ = y/x. By differentiating both sides with respect to t,
we get sec^2θ(dθ/dt) = (1/x)dy/dt,
where dθ/dt represents the rate of change of θ.
Substituting x = 5, y = 12, and dy/dt = -0.1, we find sec^2θ = 25/169.
Taking the square root of both sides, we get secθ = 13/5.
To find dθ/dt, we have (dθ/dt) = [(1/x)dy/dt] / sec^2θ = (5/169)(-0.1) / (169/25) = -25/676 rad/s.
c)
This can be determined by differentiating the equation for the area of the triangle.
The area of the triangle, A, can be expressed as A = (1/2)xy. By differentiating with respect to t, we find dA/dt = (1/2)[x(dy/dt) + y(dx/dt)], where dA/dt represents the rate of change of the area.
Substituting the given values and calculating, we find
dA/dt = (1/2)[5*(-0.1) + 12*0.6] = 3.5 m^2/s.
Thus, the rate of change of the triangle's area is 3.5 m^2/s.
To know more about the rate of change, refer here:
https://brainly.com/question/13103052#
#SPJ11
A result is called "statistically significant" whenever. O The null hypothesis is true. O The significant level a = 0.05. O The p-value Greaterthanorequalto 0.05. O The p-value is less than the significant level.
Answers
A result is called "statistically significant" when the p-value is less than the significant level, typically 0.05.
This means that there is less than a 5% chance that the results are due to chance alone, and suggests that there is a real effect present in the data.
The Null Hypothesis is the assumption that there is no significant difference between the measured phenomenon and a certain value or set of values. A statistically significant result means that the observed data are inconsistent with the assumption of no difference, or no effect.
To know more about Null Hypothesis click on the link provided below:
https://brainly.com/question/28920252#
#SPJ4
Find the area of the region between y=x^1/2 and y=x^1/5 for 0<=x<=1.
area =
Answers
The area of the region between y=x^(1/2) and y=x^(1/5) for 0<=x<=1 is 1/6 square units.
To find the area between the two curves y=x^(1/2) and y=x^(1/5) for 0<=x<=1, we will use the definite integral.
Step 1: Identify the bounds of integration. Since the question specifies 0<=x<=1, these are our bounds.
Step 2: Determine the difference between the two functions. Subtract the smaller function from the larger one: (x^(1/2)) - (x^(1/5)).
Step 3: Set up the integral. We will integrate the difference of the two functions with respect to x, from 0 to 1.
area = ∫(x^(1/2) - x^(1/5)) dx from 0 to 1
Step 4: Evaluate the integral. Using the power rule for integration, we get:
area = (2/3 * x^(3/2) - 5/6 * x^(6/5)) evaluated from 0 to 1
Step 5: Substitute the bounds and find the area.
area = [(2/3 * (1)^(3/2) - 5/6 * (1)^(6/5)) - (2/3 * (0)^(3/2) - 5/6 * (0)^(6/5))]
area = (2/3 - 5/6)
area = 1/6
The area of the region between y=x^(1/2) and y=x^(1/5) for 0<=x<=1 is 1/6 square units.
To know more about refer here:
https://brainly.com/question/27683633
#SPJ11
Clyde has a cone-shaped party hat. The height of the hat is 10 inches, and the radius of the base of the hat is 4 inches. What is the area of a vertical cross section through the center of the base of the party hat?
Answers
Check the picture below.
\(\textit{area of a triangle}\\\\ A=\cfrac{1}{2}bh~~ \begin{cases} b=base\\ h=height\\[-0.5em] \hrulefill\\ b=8\\ h=10 \end{cases}\implies A=\cfrac{1}{2}(8)(10)\implies A=40\)

The area of a vertical cross-section through the centre of the base of the party hat is 40 square inches.
What is a cone?It is defined as the three-dimensional shape in which the base is a circular shape and if we go from circular base to top the diameter of the circle reduces and at the vertex, it becomes almost zero.
Clyde has a cone-shaped party hat.
The height of the hat = 10 inches
The radius of the base of the hat = 4 inches.
The diameter of the base of the hat = 2×4 ⇒8 inches
The vertical cross-section of the cone exactly looks like a triangle.
In this scenario, the vertical cross-section of the hat is a triangle with a height of 10 inches, and base length of 8 inches.
We know the formula for the area of a triangle is given by:
\(\rm A = \frac{1}{2} (b\times h)\)
Here b = 8 inches, and h = 10 inches
\(\rm A = \frac{1}{2} (8\times 10)\)
A = 40 square inches
Thus, the area of a vertical cross-section through the centre of the base of the party hat is 40 square inches.
Learn more about the cone here:
brainly.com/question/16394302
pls help i need to pass
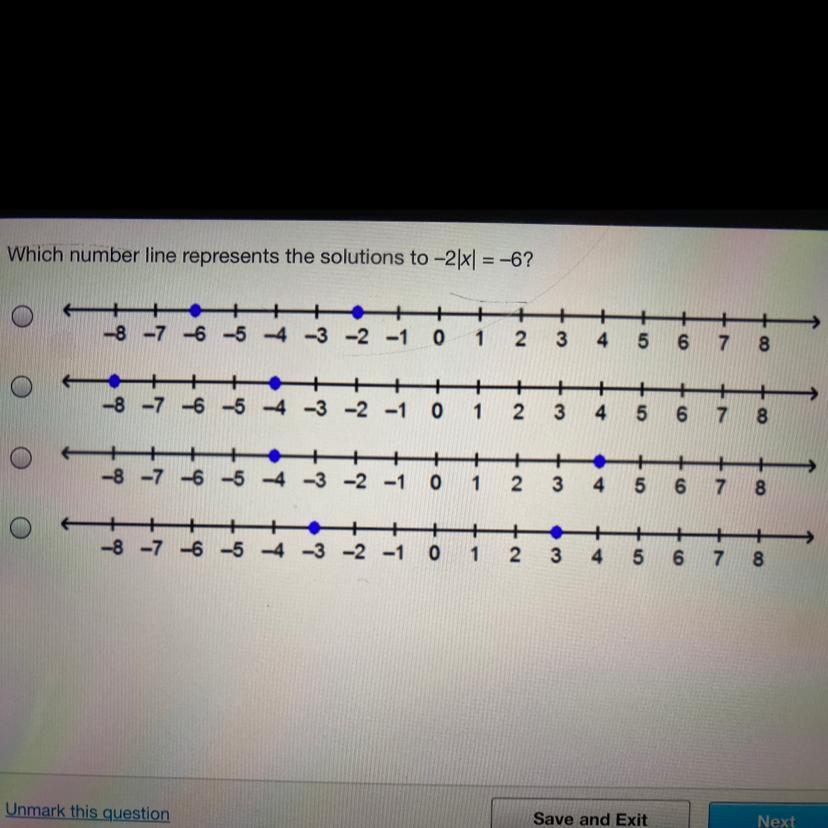
Answers
Answer:
d x=+-3
Step-by-step explanation:
divide both sides by 2
Answer:
The last one.
Step-by-step explanation:
You can begin by dividing by - 2
-2*abs(x) =-6
-2*abs(x)/-2 = - 6/-2
abs(x) = 3
So x can be -3 or 3. Both are solutions
That's the last one.
Name five large cities and their population also find their distance in kilometres between each pair of the cities
Answers
The five large cities in India are:
BangaloreMumbaiNew DelhiHyderabadKolkataThe population of large cities in India are:
The Current population of Bangalore is 11,556,907The Current population of Hyderabad is 8.7 million.The Current population of Kolkata is 5 million.The Current population of Delhi is 25 million.The Current population of Mumbai is 21 million.The distance between the large cities in India are:
The distance between Bangalore to Hyderabad is 575 kmThe distance between Mumbai to Delhi is 1136kmThe distance between Kolkata to Hyderabad is 1192km.Read more about India city
brainly.com/question/237028
#SPJ1
the side of a square are each 16 cm. A second square is inscribed by joining the midpoints of the sides successively. in the second square we repeat the process inscribed the third square. if this process is continued indefinitely what is the sum of the perimeter of all the square
Answers
The sum of the perimeters of all the squares in this infinite process is 128 cm.
To find the sum of the perimeters of all the squares in this infinite process, we can consider the relationship between the side lengths of each square.
In the initial square, the side length is 16 cm. When we inscribe the second square by joining the midpoints of the sides, the side length of the second square becomes half of the side length of the first square, which is 8 cm.
Similarly, for each subsequent square, the side length will be half of the previous square's side length.
Therefore, the side lengths of the squares in the process can be represented as 16 cm, 8 cm, 4 cm, 2 cm, 1 cm, and so on.
To find the sum of the perimeters, we need to sum the perimeters of all the squares.
The perimeter of each square is calculated by multiplying the side length by 4.
For the initial square: 16 cm * 4 = 64 cm
For the second square: 8 cm * 4 = 32 cm
For the third square: 4 cm * 4 = 16 cm
For the fourth square: 2 cm * 4 = 8 cm
For the fifth square: 1 cm * 4 = 4 cm
And so on.
To find the sum, we can add all these values together:
64 cm + 32 cm + 16 cm + 8 cm + 4 cm + ...
This is an infinite geometric series with a common ratio of 1/2.
The sum of an infinite geometric series can be calculated using the formula: sum = a / (1 - r), where 'a' is the first term and 'r' is the common ratio.
In this case, the first term (a) is 64 cm and the common ratio (r) is 1/2.
Using the formula, we have:
sum = 64 cm / (1 - 1/2) = 64 cm / (1/2) = 128 cm
Therefore, the sum of the perimeters of all the squares in this infinite process is 128 cm.
for such more question on perimeters
https://brainly.com/question/23875717
#SPJ8
brainliest if you answer correctly

Answers
Answer:
y is 1
Step-by-step explanation:
Everyone loved the Chocolate eclairs and they all got eaten during the party. Mr Watson friend, James, ate 68of them if there were16 of the chocolates, how many did James eat?
Answers
The above question was not written properly
Complete Question
Everyone loved the Chocolate eclairs and they all got eaten during the party. Mr Watson friend, James, ate 6/8 of them if there were 16 of the chocolates, how many did James eat?
Answer:
12 chocolates
Step-by-step explanation:
From the above question, we know that
Total number of Chocolates = 16
The fraction of Chocolate that James ate = 6/8
Therefore, the amount of chocolates that James ate is calculated as:
= 6/8 of 16 chocolates
= 6/8 × 16 chocolates
= 12 chocolates
Therefore, James ate 12 chocolates.
Answer: 12
Step-by-step explanation:
Number of chocolates = 16.
Fraction eaten by James = 6/8.
The number of chocolates eaten by James will be gotten by multiplying 6/8 by 16. This will be:
= 6/8 × 16
= 12
James ate 12 chocolate
there is a 5 person round table. 5 different people sit down at the table. what are the odds that sue will sit next to bob?
Answers
The probability that Sue will sit next to Bob is 96/24 = 4. So, the odds are 4:1.
We need to find out the odds that Sue will sit next to Bob. There is a round table with five different people. Therefore, the total number of ways that five different people can be seated at a round table is (5 - 1)! = 4!.
Thus, there are 24 ways that these five different people can be seated around the table. Now, let's say Sue and Bob are sitting next to each other. Thus, there are 4! = 24 ways in which they can be seated around the table. Now, Sue and Bob can be treated as a single unit since they are sitting together. So, there are a total of 48 + 48 = 96 possible ways that Sue will sit next to Bob in a 5 person round table. There are 24 possible ways that 5 people can be seated around the table.
To learn more about probability, visit:
https://brainly.com/question/32117953
#SPJ11
55x+35y=200 answers

Answers
The value of x is 2.045 by simple algebra.
Speed divided by distance equals what?Use the time formula, t = d/s, which states that time is equal to distance divided by speed, to solve for time. Time is a function of both speed and distance.
Until it reaches its destination 200 miles distant, a car is driving on a little highway at either 55 or 35 miles per hour, depending on the posted speed restrictions.
x is the duration, in hours, that the vehicle is travelling at 55 mph.
Y is the duration, in hours, that the vehicle is travelling at 35 mph.
55x + 35y = 200 is the equation defining the relationship.
We must locate:
If the trip takes the car 2.5 hours at 35 miles per hour, how long does it take to travel at 55 miles per hour?
∵ 55x + 35y = 200
The drive takes the car 2.5 hours at a speed of 35 mph.
Y shows the duration of time for an automobile travelling at 35 mph.
∴ y = 2.5
- To obtain the value of x, substitute the value of y into the equation.
∴ 55x + 35(2.5) = 200
∴ 55x + 87.5 = 200
- Take 87.5 off of both sides.
∴ 55x = 112.5
- Subtract 55 from both sides.
x equals 2.045 hours.
To know more about algebra visit:-
brainly.com/question/24875240
#SPJ1
3 One end of a cable is attached to the top of a flagpole and the other end is attached 6 feet away from the base of the pole. If the height of the flagpole is 12 feet, find the length of the cable. Cable Flagpole 12 ft Y ke 6 ft Round your answer to the nearest tenth
Answers
The length of the cable is 13.4 ft
Here, we want to find the height of the cable
By the given information in the question, we start with a diagrammatic representation of the information
We have this as follows;
As seen from above, what we have is a right-triangle, with the cable length representing the hypotenuse (the longest side)
Using Pythagoras' theorem, we can get the cable length
The square of the length of the hypotenuse is equal to the sum of the squares of the two other sides
Mathematically, we have this as follows (we are representing the length of thecable by c0
Thus, we have it that;
\(\begin{gathered} c^2=12^2+6^2 \\ c^2\text{ = 144 + 36} \\ c^2\text{ = 180} \\ \text{c = }\sqrt[]{180} \\ c\text{ = 13.4 ft} \end{gathered}\)
A charity holds a raffle in which each ticket is sold for $35. A total of 9000 tickets are sold. They raffle one grand prize which is a Lexus GS valued at $45000 along with 2 second prizes of Honda motorcycles valued at $9000 each. What are the expected winnings for a single ticket buyer? Express to at least three decimal place accuracy in dollar form (as opposed to cents).
Answer: $
Answers
A purchaser of a single ticket can anticipate losing, on average, $28.
The likelihood of winning each prize multiplied by the prize's worth, then adding up all the prizes, can be used to determine the estimated earnings for a single-ticket purchaser.
The big prize has a 1/9000 chance of being won, and it is worth $45000. Hence, the following are the anticipated profits from the main prize:
45000/9000 = 5
The odds of winning one of the three second-place prizes, each worth $9000, are 2/9000. The following is the anticipated profits from the second prize:
2/9000 * 9000 = 2
Finally, the price of the ticket itself is the projected cost of the ticket:
$35
Consequently, the difference between the expected value of the prizes and the ticket's price can be used to compute the expected wins for a single ticket purchaser:
$5 + $2- $35 = -$28
This indicates that a purchaser of a single ticket can anticipate losing, on average, $28.
To know more about probability follow
brainly.com/question/24756209
#SPJ1
If a polynomial function f(x) has roots –9 and 7 – i, what must be a factor of f(x)? (x – (7 i)) (x – (–7 – i)) (x (7 i)) (x (7 – i))
Answers
if the roots of the polynomial function are -9 and 7 - i, then the other factor of the polynomial function is x - (7 + i)
How to determine the other factor?The roots of the polynomial function are given as:
-9 and 7 - i
The root is 7 - i is a complex number.
This means that its conjugate must also be a root of the factor.
The conjugate of 7 - i is 7 + i
So, we have:
x = 7 + i
Equate to 0
x - (7 + i) = 0
Hence, the other factor of the function is x - (7 + i)
Read more about polynomial functions at:
https://brainly.com/question/2833285
#SPJ4
Answer:
A on edge 23
Step-by-step explanation:
trust me bro
Examine the diagram, where points B, C, D, and Elie on circle A. Angle BCD measures 57°. В. C A 570 D 2019 Strong Mind. Created using GeoGebra. What is mZBED?

Answers
Based on the inscribed angle theorem, the measure of angle BED in the diagram given is: 57°.
What is the Inscribed Angle Theorem?The inscribed angle theorem states the measure of the inscribed angles subtended by the same arc are the same.
∠BCD and ∠BED are subtended by the same arc BD.
Therefore, based on the inscribed angle theorem, we have:
m∠BCD = m∠BED = 57°.
m∠BED = 57°
Learn more about the inscribed angle theorem on:
https://brainly.com/question/3538263
#SPJ2
Dave buys a coat for £20, a hat for £15 and a pair of gloves for £5.
Later, he sells the coat at 50% profit. He sells the hat for £18 but has to sell the gloves at a 20% loss.
What is his overall percentage profit?
Answers
Answer:
30%
Step-by-step explanation:
Purchases:
Coat £20
Hat £15
Gloves for £5
Total amount of purchases: £20 + £15 + £5 = £40
Sales:
Coat at 50% profit: 150% × £20 = 1.5 × £20 = £30
Hat: £18
Gloves at a 20% loss: 80% of £5 = £4
Total amount of sales: £30 + £18 + £4 = £52
Amount of profit: £52 - £40 = £12
Percent of profit: £12 / £40 × 100% = 30%
The table below shows the combination of dry prepackaged mix and water to make concrete. The mix says for every 1 gallon of water stir 60 pounds of dry mix. We know that 1 gallon of water is equal to 8 pounds of water . Using the information provided in the table complete the remaining parts of the table . What belongs in Cell A?

Answers
Answer:
60
Step-by-step explanation:
The diagram shows the graph of y = x² - 4x + 6, with a tangent drawn to the
curve at x = 3.
Use the tangent to estimate the gradient of the curve at
=
3.

Answers
Mr. Taylor and Mrs. Miller’s classes have been having a fundraising competition. they’ve both kept track of how much money they’ve raised in dollars versus the time in days. while mr. taylor’s class chose to graph their data, mrs. millers class chose to present it in a table. both classes have found that their fundraising over time has been proportional, where the daily increase in money raised is consistent. please explain why you chose this answer i will mark you brainliest

Answers
at a rehearsal dinner the night before a wedding, the bride and groom need to assign 10 people to two tables of five people. how many different groups of five can they form?
Answers
The bride and groom can form 252 different groups of five people from the total of 10 people at the rehearsal dinner, as they need to assign them to two tables of five people each.
To determine the number of different groups of five people that can be formed, we can use the concept of combinations. In this scenario, we have 10 people who need to be divided into two groups of five people each.
The number of ways to choose five people out of 10 can be calculated using the combination formula. The formula for combinations is given by:
C(n, r) = n! / (r! * (n - r)!)
Where n represents the total number of people and r represents the number of people to be chosen. In this case, n = 10 and r = 5.
Plugging these values into the formula, we get:
C(10, 5) = 10! / (5! * (10 - 5)!)
= (10 * 9 * 8 * 7 * 6 * 5!) / (5! * 5 * 4 * 3 * 2 * 1)
= (10 * 9 * 8 * 7 * 6) / (5 * 4 * 3 * 2 * 1)
= 252
Therefore, the bride and groom can form 252 different groups of five people from the total of 10 people at the rehearsal dinner. This means that there are 252 distinct ways to divide the 10 people into two tables of five people each, providing flexibility in creating diverse groups for the dinner.
Learn more about divide here:
https://brainly.com/question/15381501
#SPJ11
Consider the function given below: (defun things (x) (if (null x ) '() (if (>(carx) 10) (cons(+(carx) 1) (things (cdrx))) (cons (- (car x) 1) (things (codr x)) ) 1 ) 1 Show the evolution resulting from the following call: USP> (things '(11-2 31))
Answers
The evolution of the function call (things '(11 -2 31)) is as follows:
(things '(11 -2 31)) -> (things '(-2 31)) -> (things '(31)) -> (things '()) -> '() the final result of the given call is '().
The given function is a recursive function called "things" that takes a list as input. It checks if the list is empty (null), and if so, it returns an empty list. Otherwise, it checks if the first element of the list (car x) is greater than 10. If it is, it adds 1 to the first element and recursively calls the "things" function on the rest of the list (cdr x). If the first element is not greater than 10, it subtracts 1 from the first element and recursively calls the "things" function on the rest of the list. The function then returns the result.
Now, let's see the evolution resulting from the call (things '(11 -2 31)):
1. (things '(11 -2 31))
Since the list is not empty, we move to the next if statement.
The first element (car x) is 11, which is greater than 10, so we add 1 to it and recursively call the "things" function on the rest of the list.
The recursive call is (things '(-2 31)).
2. (things '(-2 31))
Again, the list is not empty.
The first element (car x) is -2, which is not greater than 10, so we subtract 1 from it and recursively call the "things" function on the rest of the list.
The recursive call is (things '(31)).
3. (things '(31))
The list is still not empty.
The first element (car x) is 31, which is greater than 10, so we add 1 to it and recursively call the "things" function on the rest of the list.
The recursive call is (things '()).
4. (things '())
The list is now empty, so the function returns an empty list.
To know more about function visit:
brainly.com/question/30721594
#SPJ11
y varies directly as the square of x and inversely as z. Find y when x=2 and z=1 , if y=4 when x=4 and z=12
Answers
The direct and Inverse variation relationship,x = 2 and z = 1, the value of y is 12.
the direct and inverse variation relationship:
y = k * (x^2) / z
where k is the constant of variation.
Given that y = 4 when x = 4 and z = 12, we can substitute these values into the equation:
4 = k * (4^2) / 12
Simplifying, we have:
4 = k * 16 / 12
To solve for k, we can cross-multiply and divide:
4 * 12 = k * 16
48 = 16k
Dividing both sides by 16:
48 / 16 = k
k = 3
Now that we have determined the value of k, we can use it to find y when x = 2 and z = 1.
Substituting these values into the equation, we have:
y = 3 * (2^2) / 1
Simplifying further
y = 3 * 4 / 1
y = 12
Therefore, when x = 2 and z = 1, the value of y is 12.
To know more about Inverse.
https://brainly.com/question/3831584
#SPJ11
The list below shows the average monthly temperatures
in degrees Fahrenheit in Ahmed's city for the past year.
74, 86, 90, 68, 76, 64, 68, 84, 90, 94, 82, 92
Which box-and-whisker plot correctly represents the
data in the list?

Answers
The correct box-and-whisker plot is the one labeled:
Average Monthly Temperatures
64 74 84 94
The box ranges from 68 to 90, with the median at 84. The whiskers extend from 64 to 94. So, third option is the right answer.
To create a box-and-whisker plot, we need to organize the data in ascending order:
64, 68, 68, 74, 76, 82, 84, 86, 90, 90, 92, 94
Now, we can identify the key components of the box-and-whisker plot:
Minimum: 64 (the lowest value in the data set)
Lower Quartile (Q1): 68 (the median of the lower half of the data set)
Median (Q2): 84 (the middle value of the data set)
Upper Quartile (Q3): 90 (the median of the upper half of the data set)
Maximum: 94 (the highest value in the data set)
Using these values, we draw a box from Q1 to Q3, with a line marking the median (Q2). We also draw "whiskers" extending from the box to the minimum and maximum values. In this case, the box ranges from 68 to 90, with the median at 84. The whiskers extend from 64 to 94.
Therefore, the correct box-and-whisker plot is the one labeled:
Average Monthly Temperatures
64 74 84 94
The right answer is third option.
For more such question on Average
https://brainly.com/question/130657
#SPJ11
''the product of a number and three is the same as the sum of that number and six''
Answers
Answer:
3
Step-by-step explanation:
Answer:
3
Step-by-step explanation:
The number is x, then:
3x = x + 63x - x = 62x = 6x = 3The number is 3
Help im litteraly failing

Answers
The solution to the given system of linear equations is x = 3, y = -3. That is, (3, -3)
The graph of the system of equations is shown below
Solving system of linear of linear equationsFrom the question, we are to determine the apparent solution to the given system of linear equations
The given system of equations is
y = -2x + 3
y = 1/3x - 4
Set the two equations equal
That is,
-2x + 3 = 1/3x - 4
Multiply through by 3
-6x + 9 = x - 12
Add 6x to both sides of the equation
-6x + 6x + 9 = x + 6x - 12
9 = 7x - 12
Add 12 to both sides of the equation
9 + 12 = 7x - 12 + 12
21 = 7x
x = 21/7
x = 3
Substitute the value of x into the first equation
y = -2x + 3
y = -2(3) + 3
y = - 6 + 3
y = - 3
The solution is (3, -3)
The graph is shown below
Learn more on Solving system of linear equations here:
#SPJ1

Determine the no-arbitrage price today of a 5 year $1,000 US
Treasury note with a coupon rate of 2% and a YTM of 4.25% (APR) (to
the penny)
A. $739.65
B. $900.53
C. $819.76
D. $89
Answers
The no-arbitrage price today of a 5-year $1,000 US Treasury note with a 2% coupon rate and a 4.25% yield to maturity is approximately $908.44, closest to option B: $900.53.
To determine the no-arbitrage price of a 5-year $1,000 US Treasury note with a coupon rate of 2% and a yield to maturity (YTM) of 4.25%, we can use the present value of the future cash flows.First, let's calculate the annual coupon payment. The coupon rate is 2% of the face value, so the coupon payment is ($1,000 * 2%) = $20 per year.The yield to maturity of 4.25% is the discount rate we'll use to calculate the present value of the cash flows. Since the coupon payments occur annually, we need to discount them at this rate for five years.
Using the present value formula for an annuity, we can calculate the present value of the coupon payments:PV = C * (1 - (1 + r)^-n) / r,
where PV is the present value, C is the coupon payment, r is the discount rate, and n is the number of periods.
Plugging in the values:PV = $20 * (1 - (1 + 0.0425)^-5) / 0.0425 = $85.6427.
Next, we need to calculate the present value of the face value ($1,000) at the end of 5 years:PV = $1,000 / (1 + 0.0425)^5 = $822.7967.
Finally, we sum up the present values of the coupon payments and the face value:No-arbitrage price = $85.6427 + $822.7967 = $908.4394.
Rounding to the penny, the no-arbitrage price is $908.44, which is closest to option B: $900.53.
To learn more about discount rate click here
brainly.com/question/31318990
#SPJ11
Write an equation in slope-intercept form of the line that passes through the given point and is perpendicular to the graph of the given equation
(-3,8): y = 1/3x -3
Answers
Answer:
y = -3x + 8
Step-by-step explanation:
the base of a triangle is shrinking at a rate of 2 cm/min and the height of the triangle is increasing at a rate of 3 cm/min. find the rate (in cm2/min) at which the area of the triangle changes when the height is 38 cm and the base is 32 cm.
Answers
When the height is 38 cm and the base is 32 cm, the rate at which the area of the triangle changes is 10 cm²/min.
The rate at which the area of a triangle changes can be found by multiplying the rate at which the base is shrinking by the rate at which the height is increasing.
Given:
Rate of shrinking of the base = -2 cm/min
Rate of increasing of the height = 3 cm/min
Height of the triangle = 38 cm
Base of the triangle = 32 cm
To find the rate at which the area of the triangle changes, we use the formula for the area of a triangle:
Area = (1/2) * base * height
Differentiating the area formula with respect to time gives us:
dA/dt = (1/2) * (db/dt) * height + (1/2) * base * (dh/dt)
Substituting the given values, we have:
dA/dt = (1/2) * (-2) * 38 + (1/2) * 32 * 3
Simplifying, we get:
dA/dt = -38 + 48
dA/dt = 10 cm²/min
Therefore, when the height is 38 cm and the base is 32 cm, the rate at which the area of the triangle changes is 10 cm²/min.
To know more about triangle refer here:
https://brainly.com/question/2773823
#SPJ11
if g % h is cyclic, prove that g and h are cyclic. state the general case.
Answers
The general case when G₁⊕G₂⊕G₃...⊕Gₙ is cyclic generated by (g₁, g₂, g₃,...,gₙ) is that the subgroups G₁, G₂, G₃,...., Gₙ are cyclic generated by g₁, g₂, g₃, ..., gₙ respectively.
G⊕H is cyclic
That is G⊕H = <(g, h)>
Let us choose an arbitrary element g₁ ∈ G, then as G⊕H is cyclic
(g₁, h₁) ∈ G⊕H = <( g, h)>
This means that there exists an integer x such that
(g₁, h₁) = (g, h)ˣ
(g₁, h₁) = (gˣ, hˣ)
that is g₁ = gˣ
implies g₁ ∈ <g>
that is G ⊆ <g> as g₁ is an arbitrary element belonging to G
But we know <g> ⊆ G
Hence G = <g>
Thus G is a cyclic group generated by g.
Similarly we can prove that H group is cyclic generated by h, that is H = <h>
So the general case is that G₁⊕G₂⊕G₃...⊕Gₙ is cyclic generated by (g₁, g₂, g₃,...,gₙ), then the subgroups G₁, G₂, G₃,...., Gₙ are cyclic generated by g₁, g₂, g₃, ..., gₙ respectively.
To know more on cyclic groups
https://brainly.com/question/30002696
#SPJ4
Help me to do this question

Answers
Answer:
140°
Step-by-step explanation:
a° = 180°-(75°-35°) = 180°-40° = 140°