The spacecraft is designed to leave the surface of Mars with the first stage of its propulsion system and be put into Martian orbit. Then, the second stage is used to boost the spacecraft from Martian orbit into an interplanetary trajectory and return to Earth. If the spacecraft is in Martian orbit at an altitude of 384 km, what is the velocity required to escape the gravitational attraction of Mars. Give your answer in km/s. Note that the velocity direction and magnitude required to actually return to Earth may be different.
Answers
The velocity required to escape the gravitational attraction of Mars is 5.03 km/s.
To calculate the velocity required to escape the gravitational attraction of Mars, we need to find the escape velocity at the given altitude. The formula for escape velocity is:
ve = sqrt((2 * G * M) / r)
where ve is the escape velocity, G is the gravitational constant (approximately 6.674 × 10^-20 km³/kg·s²), M is the mass of Mars (approximately 6.417 × 10^23 kg), and r is the distance from the center of Mars to the spacecraft.
Given that the spacecraft is at an altitude of 384 km, we first need to add this to the radius of Mars (approximately 3,390 km) to get the distance r:
r = 3,390 km + 384 km = 3,774 km
Now we can plug these values into the escape velocity formula:
ve = sqrt((2 * 6.674 × 10^-20 km³/kg·s² * 6.417 × 10^23 kg) / 3,774 km)
ve ≈ 5.03 km/s
So, the velocity required to escape the gravitational attraction of Mars at an altitude of 384 km is approximately 5.03 km/s. Keep in mind that the velocity direction and magnitude required to actually return to Earth may be different.
For more such questions on Escape velocity.
https://brainly.com/question/14297933#
#SPJ11
Related Questions
The table of values below represent an exponential function. Find the constant ratio of successive y-values
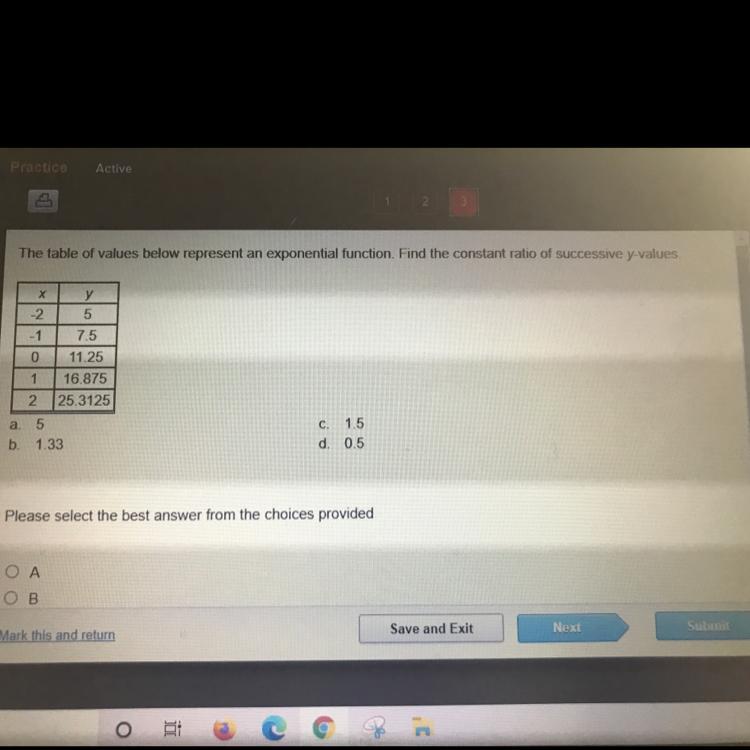
Answers
Explanation:
Answer:
The answer is C
Step-by-step explanation:
Edge 2022
A recipe for crumb cake says to mix 3/8 cup of brown sugar and 1/3 cup of white sugar.
From this sugar mixture, set aside 1/4 cup for the crumb topping.
The remaining sugar mixture is used to make the cake.
What amount of the sugar mixture is used to make the cake?
A.) 17/24
B.) 11/24
C.) 1/2
D.) 7/12
Answers
Answer:
C) 1/2
Step-by-step explanation:
We know that 3/8 cup of brown sugar and 1/3 cup of white sugar are mixed together to make the sugar mixture.
From this sugar mixture, 1/4 cup is set aside for the crumb topping.
To find out how much sugar mixture is used to make the cake, we need to subtract the amount set aside for the crumb topping from the total sugar mixture.
We can start by converting the mixed unit of measurement (brown sugar in cups and white sugar in cups) to a single unit of measurement (cups)
3/8 cup of brown sugar + 1/3 cup of white sugar = (3/8)+(1/3) = 5/12 cup + 4/12 cup = 9/12 cup.
1/4 cup is set aside for the crumb topping.
So, the remaining sugar mixture used to make the cake is 9/12 cup - 1/4 cup = (9/12) - (1/4) = (9-3)/12 = 6/12 cup = 0.5 cup
IllH1f1LHw/formResponse
Other:
Clear selection
Tiger Woods drives a golf ball a horizontal distance of 285 yards. If the ball 4 points
reached a maximum height of 40 yards, what is the parabolic equation
that models the path of the golf ball? Show the work (at least 3 steps) you
would take to find an equation that models the situation. Show the
equation at the end.
Answers
Given the functions f and g below, find g(ƒ(1)). Provide your answer below: g(f(1)) = f(x) = x + 1 g(x) = -2x²-3x+5
Answers
According to the given question we finally calculated the values and we have functions Therefore, g(f(1)) = -9.The value of g(f(1)) is -9.Thus, g(f(1)) = -9.
The given functions are: f(x) = x + 1g(x) = -2x²-3x+5 .
We have to find the value of g(f(1)).To find g(f(1)), we first need to find f(1).
So, substituting 1 in the expression of f(x), we get: f(1) = 1 + 1 = 2 .
g(f(1)) = f(x) = x + 1 g(x) = -2x²-3x+5 = ?
Now, we need to substitute this value of f(1) in the expression of g(x).
g(f(1)) = g(2) = -2(2)² - 3(2) + 5= -2(4) - 6 + 5= -8 - 1= -9 .
Therefore, g(f(1)) = -9.The value of g(f(1)) is -9.Thus, g(f(1)) = -9.
To know more about Values visit :
https://brainly.com/question/30145972
#SPJ11
8. Solve the compound inequality.8x2-64 and 10x <60-8 < x <6-8 < x <6-82x≤6-8 < x≤6

Answers
Answer:
\(-8\text{\operatorname{\leq}}\text{x}\lt\text{6}\)Explanation:
Here, we want to solve the given inequality
We proceed as follows:
\(\begin{gathered} 8x\text{ }\ge\text{ -64 and 10x }<\text{ 60} \\ x\text{ }\ge\text{ -}\frac{64}{8}\text{ and x}<\text{ }\frac{60}{10} \\ \\ x\ge\text{ -8 and x}<\text{ 6} \\ -8\text{ }\leq\text{ x}<\text{ 6} \end{gathered}\)
how many rolls of the ribbon should Quincy buy? explain your the answer
Answers
Answer:
um.. as many needed lol
Step-by-step explanation:
I just need level two and three solved please

Answers
Answer:
intercepts: (0, 5/2) or (-5, 0)arbitrary point: (7, 6)Step-by-step explanation:
You want two methods of choosing points on the line with slope 1/2 through A(-1, 2).
InterceptsWriting the equation in standard form, we can find the x- and y-intercepts. To get there, we can start from point-slope form:
y -k = m(x -h) . . . . . . line with slope m through point (h, k)
y -2 = 1/2(x -(-1)) . . . . . using given slope and point
2y -4 = x +1 . . . . . . . . . . multiply by 2
x -2y = -5 . . . . . . . . . . . . add -1 -2y
Setting x=0 tells us the y-intercept is ...
0 -2y = -5
y = -5/-2 = 5/2
So, the y-intercept is (0, 5/2).
Setting y=0 tells us the x-intercept is ...
x -2(0) = -5
x = -5
So, the x-intercept is (-5, 0).
Arbitrary pointIt will be convenient to choose an arbitrary y-value to find another point on the line. We can pick y = 6, for example, Then the corresponding x-value is ...
x -2y = -5
x = -5 +2y = -5 +2(6) = 7
Another point on the line is (7, 6).
__
Additional comment
If we were to choose an arbitrary value for x, we would want it to be odd, so the corresponding y-value would be an integer. We chose to pick an arbitrary value of y so we didn't have to worry about how to make the x-value an integer.
<95141404393>

What is 223,692 divided by 42 using the standard algorithm and showing work?
Answers
The value of 223,692 divided by 42 using the standard algorithm and showing work is 5326.
What is division?Division is the process of splitting a number or an amount into equal parts. Division is one of the four basic operations of arithmetic, the ways that numbers are combined to make new numbers. The other operations are addition, subtraction, and multiplication.
here, we have,
The value of 223,692 divided by 42 using the standard algorithm and showing work is given below:
Dividing the two values by 2, a common factor
223,692 / 42
= 111,846 / 21
Dividing the two values by 3, a common factor
111,846 / 21
= 37282 / 7
Dividing the two values by 7, a common factor
37282 / 7
= 5326 / 1
Hence, the value of the division is 5326.
Learn more about the division of numbers at: brainly.com/question/25289437
#SPJ1
Help please please please

Answers
Dggdxbjhtddcbgdxcvghdf
Answer:
it's true
Step-by-step explanation:
and what is you grade I can be your tutor if you want jk
write 17/20 as a fraction decimal percent.
Answers
Written as a fraction, the amount is 17/20 .
But a fraction actually means "division". When you see "17/20", it means "17 divided by 20".
If you actually go ahead and DO the division problem (with a pencil or on your calculator) that the fraction is talking about, the answer you get is the same amount as the fraction, but written as a decimal.
The same amount as 17/20, written as a decimal, is 0.85 .
The same amount as 17/20, written as a percent, is 85% .
What is the area of a rectangle with length 4 cm and width 12 cm?
16 cm2
48 cm2
3 cm2
32 cm2
Answers
Answer:
option 2 = 48 cm ²
12 × 4 = 48
cm × cm = cm²
answer = 48 cm²
how to find eigenvalues and eigenvectors of a 2x2 matrix
Answers
To find the eigenvalues and eigenvectors of a 2x2 matrix, follow these steps:
Calculate the characteristic equation by subtracting the identity matrix I multiplied by the scalar λ from matrix A, and set the determinant of this resulting matrix equal to zero. The characteristic equation is given by det(A - λI) = 0.Solve the characteristic equation to find the eigenvalues (λ).
Let's assume we have a 2x2 matrix A:
| a b |
A = | c d |
To find the eigenvalues, we need to calculate the characteristic equation:
det(A - λI) = 0,
where I is the 2x2 identity matrix and λ is the eigenvalue.
A - λI = | a-λ b |
| c d-λ |
The determinant of this matrix is:
(a-λ)(d-λ) - bc = 0,
which simplifies to:
λ² - (a+d)λ + (ad - bc) = 0.
This quadratic equation gives us the eigenvalues.
Solve the quadratic equation to find the values of λ. The solutions will be the eigenvalues.
Once you have the eigenvalues, substitute each value back into the equation (A - λI)v = 0 and solve for v to find the corresponding eigenvectors.
For each eigenvalue, set up the homogeneous system of equations:
(A - λI)v = 0,
where v is the eigenvector.
Solve this system of equations to find the eigenvectors corresponding to each eigenvalue.
To find the eigenvalues and eigenvectors of a 2x2 matrix, follow the steps mentioned above. The characteristic equation gives the eigenvalues, and by solving the corresponding homogeneous system of equations, you can determine the eigenvectors.
To know more about eigenvalues, visit
https://brainly.com/question/29861415
#SPJ11
Answer it please???
//

Answers
2 triangles: 8(15)/2=60
rectangle 1: 17(2)=34
rectangle 2: 15(2)=30
rectangle 3: 8(2)=16
SA= 60+60+34+30+16
SA=200mm
80 board game is on sale for 20 percent off
How much is the board game?
Answers
Answer:
the answer is 64 dollars or pounds or whichever currency
Answer:
The bord game is 64$.
Step-by-step explanation:
80/10=8
8*(8-2)=
64$
Type the correct answer in the box. use numerals instead of words. a population of beetles increases by 5% every year. if at the start of the year the population is at 10,000 beetles, what will its population be after three years? at the end of the third year the population of beetles will be .
Answers
At the end of the third year the population of beetles will be 11,576beetles
Exponential equationsThe standard form of an exponential function is given as:
y = ab^t
Given the following parameters
initial population 'a" = 10,000 beetles
Time = 3 years
rate b = 1.05
Substitute into the formula
y = 10,000(1.05)^3
y = 10,000(1.1576)
y = 11,576 beetles
Hence at the end of the third year the population of beetles will be 11,576beetles
Learn more on exponential function here: https://brainly.com/question/12940982
#SPJ4
What is the inequality
1.2 + m≤ 5.5
Answers
Answer: The inequality is:
1.2 + m ≤ 5.5
This inequality can be read as "the sum of 1.2 and m is less than or equal to 5.5."
To solve for m, you need to isolate it on one side of the inequality symbol.
1.2 + m ≤ 5.5
Subtract 1.2 from both sides:
m ≤ 5.5 - 1.2
Simplify:
m ≤ 4.3
Therefore, the solution to the inequality is m ≤ 4.3.
Step-by-step explanation:
What is the decimal equivalent of 7/12?
Answers
Answer:
0.5833333.......
Step-by-step explanation:
All you have to do is divide 7 by 12. The fraction 7/12 is equal to 7 ÷ 12.
7 ÷ 12 = 0.583... (repeating 3)
Or if you round, you have 0.58.
what value of z* should be used to construct a 99% confidence interval of a population mean? answer choices are rounded to the hundredths place.
Answers
The value of z* to construct a 99% confidence interval is 2.58.
How to find the value of z*?The value of z* that can be used to construct confidence interval can be calculated or find out in many ways. But, usually and the easiest way is by look the value in T table.
The value of z* is equal to the value of critical value in t table. So, to find it we search the column of 99% confidence level or if use the one tail is equal to 0.005 or if use the two tail is equal to 0.01. Then, we search the row of z, after that we get the value of 2.576.
Attached image for t table.
Thus, the value of z* for 99% confidence interval is 2.58.
Learn more about confidence interval here:
brainly.com/question/15712887
#SPJ4

the mean waiting time at the drive-through of a fast-food restaurant form the time an order is placed to the time the order is received is 84.3 seconds. a manager devises a new drive-through system that he believes will decrease the wait time. to test his claim, he initiates the new system at his restaurant and measures the wait time for 45 randomly selected orders and finds the sample mean to be 79.1 and a sample standard deviation of 17.3. has the wait time significantly decreased?
Answers
Yes, the wait time significantly decreased after implementing the new system, based on hypothesis testing.
How to determine if wait time significantly decreased?To determine if the wait time has significantly decreased, we can conduct a hypothesis test using the one-sample t-test. The null hypothesis, denoted as H0, is that the population mean waiting time is still 84.3 seconds, while the alternative hypothesis, denoted as Ha, is that the population mean waiting time has decreased to less than 84.3 seconds.
Let's set the significance level at α = 0.05. Since the sample size is large (n = 45), we can use the t-distribution to conduct the hypothesis test. The test statistic can be calculated as:
t = (sample mean - population mean) / (sample standard deviation / sqrt(sample size))
t = (79.1 - 84.3) / (17.3 / sqrt(45))
t = -2.16
Using a t-distribution table or calculator with 44 degrees of freedom
(df = n - 1), the p-value for this test is found to be approximately 0.018.
Since the p-value (0.018) is less than the significance level (0.05), we reject the null hypothesis. This means we have evidence to suggest that the wait time has significantly decreased after implementing the new drive-through system.
Therefore, based on the given data, we can conclude that the wait time has significantly decreased at the fast-food restaurant after implementing the new drive-through system.
Learn more about significantly decreased
brainly.com/question/3612236
#SPJ11
-4r-7+10r=-7+6r one solution
Answers
Answer/Step-by-step explanation:
-4r - 7 + 10r = -7 + 6r
6r - 7 = -7 + 6r
+7 +7
6r = 6r
This equation is true
All real numbers (-∞, ∞)
I hope this helps!
A bank in London, Ontario has a buying rate of CHF1=C$1.2927. If the exchange rate is CHF1=C$1.3221, calculate the rate of commission that the bank charges. % Round to two decimal places
Answers
To calculate the rate of commission charged by the bank in London, Ontario, we can compare the buying rate and the exchange rate for the Swiss Franc (CHF) to Canadian Dollar (C$) currency pair. By finding the difference between the buying rate and the exchange rate as a percentage of the exchange rate, we can determine the rate of commission.
The rate of commission charged by the bank can be calculated using the following formula:
Commission Rate = \(\(\left(\frac{{Exchange\ Rate - Buying\ Rate}}{{Exchange\ Rate}}\right) \times 100\%\)\)
In this case, the buying rate is CHF1 = C$1.2927, and the exchange rate is CHF1 = C$1.3221.
Substituting the values into the formula, we can calculate the rate of commission:
Commission Rate =\(\(\left(\frac{{1.3221 - 1.2927}}{{1.3221}}\right) \times 100\% \approx 2.23\%\)\)
Therefore, the rate of commission charged by the bank in London, Ontario, is approximately 2.23%.
Learn more about percentage here:
https://brainly.com/question/16797504
#SPJ11
Option 2:
Find m < C. Show all work.

Answers
Answer:
m∠C = 28.1°
Explanation:
angle m∠C has opposite angle of 16 and hypotenuse of 34
using sine rule:
\(\boxed{ sin(C) = \frac{opposite}{hypotenuse}}\)
\(sin(C)=\frac{16}{34}\)
\(C = sin^{-1}(\frac{16}{34} )\)
C = 28.07248°
C = 28.1°
\(\\ \tt\Rrightarrow tanC=\dfrac{AB}{BC}\)
\(\\ \tt\Rrightarrow tanC=\dfrac{16}{30}\)
\(\\ \tt\Rrightarrow tanC=0.53\)
\(\\ \tt\Rrightarrow C=tan^{-1}(0.53)\)
\(\\ \tt\Rrightarrow C=27.92°\)
Please help, it’s due tonight. I do have my answer I just need help explaining how it work for any number..

Answers
Answer:
Yes it is 10!
Step-by-step explanation:
5+20=25
25x5=125
125+125=250
250-200=50
50/5=10
There were 17 students running in a race. How many different arrangements of first, second, and third place are possible?
Answers
There are 4,080 different arrangements of first, second, and third place possible for the 17 students running in the race.
To determine the number of different arrangements of first, second, and third place, we need to use the permutation formula.
The number of permutations of n objects taken r at a time is given by:
P(n,r) = n!/(n-r)!
In this problem, we have 17 students running, and we want to determine the number of different arrangements of first, second, and third place, which means we need to find the number of permutations of 17 objects taken 3 at a time.
Using the permutation formula, we get:
P(17,3) = 17!/(17-3)!
= 17!/14!
= 171615
= 4,080
Therefore, there are 4,080 different arrangements of first, second, and third place possible for the 17 students running in the race.
for such more question on permutation
https://brainly.com/question/1216161
#SPJ11
william can mulch a garden in 20 minutes. together, william and tina can mulch the same garden in 11 minutes. how long will it take tina to mulch the garden when working alone?
Answers
Tina can mulch the garden alone in 25 minutes.
Let's use the formula for the work rate to solve the problem. If William can mulch the garden alone in 20 minutes, his work rate is 1/20. Similarly, let's assume that Tina can mulch the garden alone in x minutes, so her work rate is 1/x.
When they work together, their work rates add up, so we have:
1/20 + 1/x = 1/11
Now we can solve for x:
1/x = 1/11 - 1/20
1/x = (20 - 11) / (11 x 20)
1/x = 9 / 220
x = 220 / 9
x ≈ 24.4
So it would take Tina 24.4 minutes to mulch the garden alone.
However, we need to round this up to the nearest minute because you can't have a fraction of a minute. Therefore, Tina can mulch the garden alone in 25 minutes.
Alternatively, we can use the inverse formula for the work rate to solve for Tina's time alone:
1/20 + 1/t = 1/11
1/t = 1/11 - 1/20
1/t = (20 - 11) / (11 x 20)
1/t = 9 / 220
t = 220 / 9
t ≈ 24.4
So Tina can mulch the garden alone in 24.4 minutes, which rounds up to 25 minutes.
To know more about work rate, refer here:
https://brainly.com/question/29064611#
#SPJ11
part A: if McDonald's wanted to fence in the square where pasture and Barbed wire fencing cost a $1.50 per foot, then determine the cost to fence in the pasture.Part b: if MacDonald wants to cover the square pasture and fertilizer and then he needs to determine the area of the pasture. What is the area of the pasture in the nearest hundredth?
Answers
A) To fence the squere, we have to calculate the perimeter of the figure so first we have to calculate the side of the square, so we can use the trigonometric identity of sin so:
\(\sin (45)=\frac{x}{750}\)and we solve for x so:
\(\begin{gathered} x=750\sin (45) \\ x=530.33 \end{gathered}\)Now the perimeter will be:
\(\begin{gathered} P=530.33\cdot4+750 \\ P=2871.32 \end{gathered}\)Now the cost will be the perimeter times the cost per foot so:
\(\begin{gathered} C=2871.32\cdot1.50 \\ C=4306.98 \end{gathered}\)B) The are of the pasture will be the addition of the area of the squate plus the area of the triangle so:
\(\begin{gathered} A=A_t+A_s \\ A=\frac{530.33\cdot530.33}{2}+530.33\cdot530.33 \\ A=530.33+1060.66 \\ A=1590.99 \end{gathered}\)Use Descartes' Rule of Signs to determine how many positive and how many negative real zeros the polynomial can have. Then determine the possible total number of real zeros. (Enter your answers as comma-separated lists.)
P(x) = x^3 − x^2 − x − 5
number of positive zeros possible number of negative zeros possible number of real zeros possible
Answers
According to Descartes' Rule of Signs, there is 1 positive real zero and 2 or 0 negative real zeroes of the polynomial.
Descarte's Rule of Signs determines the number of real zeros in polynomial functions.
This indicates that -
The number of positive real zeros in the polynomial function f(x) is less than or equal to an even number depending on the sign change of the coefficients.
The number of negative real zeros in f(x) is an even number equal to or less than the number of sign changes of the coefficients of f(-x) terms.
Here, the polynomial function is given as -
\(P(x)=x^{3}-x^{2} -x-5\) ----- (1)
We have to find out the number of positive and negative real zeros that the given polynomial can have.
The given polynomial already has its variables in the descending powers. So, we can easily determine the number of sign changes in the coefficients of P(x).
So, the coefficients of the variables in P(x) are -
1, -1, -1, -5
From above, we see that -
There is a sign change in the first and second variable coefficients
There is no sign change in the second and third variable coefficients
There is no sign change in the third and fourth variable coefficients
According to Descartes' Rule of Signs, there can be exactly three positive real zeros or less than three but an odd number of zeros.
So, we can determine that the number of positive real zeroes of the given polynomial can be 1.
To find out the negative real zeroes of the given polynomial, we have to find out P(-x) and determine the sign changes in the variable coefficients of P(-x).
From equation (1), we can write P(-x) as -
\(P(x)=x^{3}-x^{2} -x-5\\= > P(-x)=(-x)^{3}-(-x)^{2} -(-x)-5\\= > P(-x)=-x^{3}-x^{2} +x-5\)----- (2)
So, the coefficients of the variables in P(-x) are -
-1, -1, +1, -5
From above, we see that -
There is no sign change in the first and second variable coefficients
There is a sign change in the second and third variable coefficients
There is a sign change in the third and fourth variable coefficients
According to Descartes' Rule of Signs, since there are two sign changes of the coefficient variables, there can be two negative real zeros or less than two but an even number of zeros.
So, we can determine that the number of negative real zeroes of the given polynomial can be 2 or 0.
Thus, according to Descartes' Rule of Signs, there is 1 positive real zero and 2 or 0 negative real zeroes of the polynomial.
To learn more about Descartes' Rule of Signs visit https://brainly.com/question/28747313
#SPJ4
suppose a simple random sample of 150 students is drawn from a population of 3000 college students. among sampled students, the average iq score is 115 with a standard deviation of 10. what is the point estimate? group of answer choices 3000 115 unable to tell. not enough information given. 10
Answers
115.
The point estimate for the average IQ score of the population of 3000 college students based on a simple random sample of 150 students with an average IQ score of 115 and a standard deviation of 10 is 115.
Therefore, the correct option is 115.
A point estimate is an estimate of a population parameter based on a single value or point. It is obtained by using statistics collected from a sample to infer population values. It can be a single value or a range of values that best represents the unknown population parameter.
Based on the given information, a simple random sample of 150 students is drawn from a population of 3000 college students.
Among sampled students, the average IQ score is 115 with a standard deviation of 10. The point estimate, in this case, is the average IQ score of the population, which is estimated to be 115 based on the sample data.
To learn more about point estimate visit:
https://brainly.in/question/11334285
#SPJ1
Factor 39+ 48. Write your answer in the form a(b + c) where a is the GCF of 39 and 48.
Answers
3(13+16) hope this helps you with your problem.
consider the infinite geometric series: what is a1? what is r? find the following partial sums: s2
Answers
An infinite geometric series is one in which each term is equal to the preceding term multiplied by a fixed non-zero number, known as the common ratio.
The first term is called a1, and the common ratio is represented by r.In this particular question, we are required to find the value of a1 and r for an infinite geometric series. The partial sum S2 will also need to be found.For a geometric sequence that is infinite, the formula for the partial sum, Sn, is:Sn = a1 / (1-r), where a1 is the first term and r is the common ratio.To solve for a1, it is necessary to know two other variables: the common ratio r and the value of the first term a1. S2 is the sum of the first two terms, so: S2 = a1 + arTo find S2, we must first determine a1 and r. a1 is the first term in the sequence, and r is the common ratio. We can obtain both a1 and r by dividing the second term by the first term.The formula is:r = (ar/a1) = a2/a1 Substitute the value of r and a1 into the formula for S2 to obtain the result: S2 = a1 + ar = a1 + a1r = a1(1+r) Therefore, the value of a1 is a constant number that will appear in the series, and the common ratio, r, will be multiplied by this number to obtain the next value in the series.
So, a1 is the first term, and r is the common ratio of the infinite geometric series. S2, the sum of the first two terms, is found by using the formula S2 = a1 + ar where a1 is the first term and r is the common ratio.
To know more about Geometric series visit-
https://brainly.com/question/30264021
#SPJ11