The sum of 2 numbers is 27. The larger number is 3 times more than the smaller number. What are the numbers?
Answers
Answer:
The first number is 6.75
The second number is 20.25
Step-by-step explanation:
I went into decimals
Related Questions
Twice a number is five less than three times the
number" translates to
Answers
Answer:
Step-by-step explanation:
2n = 3n - 5
This works out to n = 5.
The translates of ''Twice a number is five less than three times the number" as,
⇒ 2 x = 3 x - 5
Here,
The written expression is,
''Twice a number is five less than three times the number" .
What is Mathematical expression?
An expression in math is a sentence with a minimum of two numbers or variables and at least one math operation.
Now,
The written expression is,
''Twice a number is five less than three times the number" .
Let a number is ' x '.
Then, in mathematical expression it can be written as,
⇒ 2 x = 3 x - 5
After solving this, we get;
2 x = 3 x - 5
x = 5
So, The translates of ''Twice a number is five less than three times the number" as,
2 x = 3 x - 5
Learn more about the Mathematical expression visit:
https://brainly.in/question/20351860
#SPJ2
Three friends are planning to visit each other. To optimize travel time, they want the meeting place to be equidistant from the three different cities they live in. The cities are located at A(-16, -1), B(1, 6), and C(1, -18). What are the coordinates where the meeting should take place?
A. (-7,-9.5)
B.(-7.5,2.5)
C. (-4,-6
D.(-4.3,-4.3)
Answers
The coordinates of the meeting place are approximately (-4.3, -4.3).
Option D is the correct answer.
We have,
Now,
Midpoint between cities A and B:
(((-16+1)/2), ((-1+6)/2)) = (-7.5, 2.5)
Midpoint between cities A and C:
(((-16+1)/2), ((-1-18)/2)) = (-7.5, -9.5)
Midpoint between cities B and C:
(((1+1)/2), ((6-18)/2)) = (1, -6)
Now we can find the intersection of the three lines formed by these midpoints.
One way to do this is to use the point-slope form of the equation of a line.
y - y1 = m(x - x1)
where (x1, y1) is a point on the line and m is the slope of the line.
The line passing through (-7.5, 2.5) and (-7.5, -9.5):
x = -7.5
The line passing through (-7.5, 2.5) and (1, -6):
y = (-8/9)x + 35/9
The line passing through (-7.5, -9.5) and (1, -6):
y = (3/5)x - 33/5
Solving for the intersection of these lines.
x = -4.3
y = -4.3
Therefore,
The coordinates of the meeting place are approximately (-4.3, -4.3).
Learn more about coordinates here:
https://brainly.com/question/13118993
#SPJ1
Which is the graph of f(x) = 1/4 (4)?

Answers
Answer:
It's going to be the graph with the straight line that intersects through 0,1 and 2,1 and 3,1 and so on.
Step-by-step explanation:
What is the distance between (2,3) and (-2,7)? Round to the nearest tenth
Answers
Answer:
Step-by-step explanation:
distance = \(\sqrt{(7-3)^2+(-2-2)^2\) = \(\sqrt{16+16} = \sqrt{32}\), which is approximately 5.65685
Answer:
5.7
Step-by-step explanation:
\( \sqrt{(2 + 2) {}^{2} + (3 - 7) {}^{2} } = \sqrt{ {4}^{2} + {4}^{2} } = \sqrt{16 + 16} = \sqrt{32} = 4 \sqrt{2} = 5.7\)
whats the answer for shrinking -12(5/6x-5)+2x
Answers
Answer: 12x-60
Step-by-step explanation:
-12 x 5/6 = 10
-12 x 5 = -60
10x-60+2x
12x-60
Adriana y Luisa fueron a la feria y decidieron subirse a la rueda de la fortuna. Si el diámetro de la rueda es de 8 metros, ¿Qué recorrido hicieron dando una vuelta completa? Considera Pi= 3.14
Answers
Answer:
Translation?
Step-by-step explanation:
A ball is released at the left end of three different tracks. The tracks are bent from equal-length pieces of channel iron.
a. From fastest to slowest, rank the speeds of the balls at the right ends of the tracks.
b. From longest to shortest, rank the tracks in terms of the times for the balls to reach the ends.
c. From greatest to least, rank the tracks in terms of the average speeds of the balls. Or do all the balls have the same average speed on all three tracks?
Answers
a. From fastest to slowest, the speeds of the balls at the right ends of the tracks will depend on the curvature of the tracks.
If the tracks are of equal length but have different curvatures, the ball on the track with the least curvature will have the highest speed, followed by the ball on the track with the next least curvature, followed by the ball on the track with the most curvature.
b. From longest to shortest, the tracks in terms of the times for the balls to reach the ends will depend on the curvature of the tracks. If the tracks are of equal length but have different curvatures, the track with the most curvature will have the longest time for the ball to reach the end, followed by the track with the next most curvature, followed by the track with the least curvature.
c. From greatest to least, the tracks in terms of the average speeds of the balls will depend on the curvature of the tracks. If the tracks are of equal length but have different curvatures, the track with the least curvature will have the highest average speed, followed by the track with the next least curvature, followed by the track with the most curvature.
All the balls will have the same average speed on all three tracks if the track lengths are equal, but will have different speeds at the end of each track due to the different curvatures.
know more about speeds here
https://brainly.com/question/28224010#
#SPJ11
On a zip-line course, you are harnessed to acable that travels through the treetops. Youstart at platform A and zip to each of the otherplatforms. How far do you travel from Platform B to Platform C?The distance from platform B to platform C is approximately _____meters.(Round to the nearest tenth of a meter as needed.)
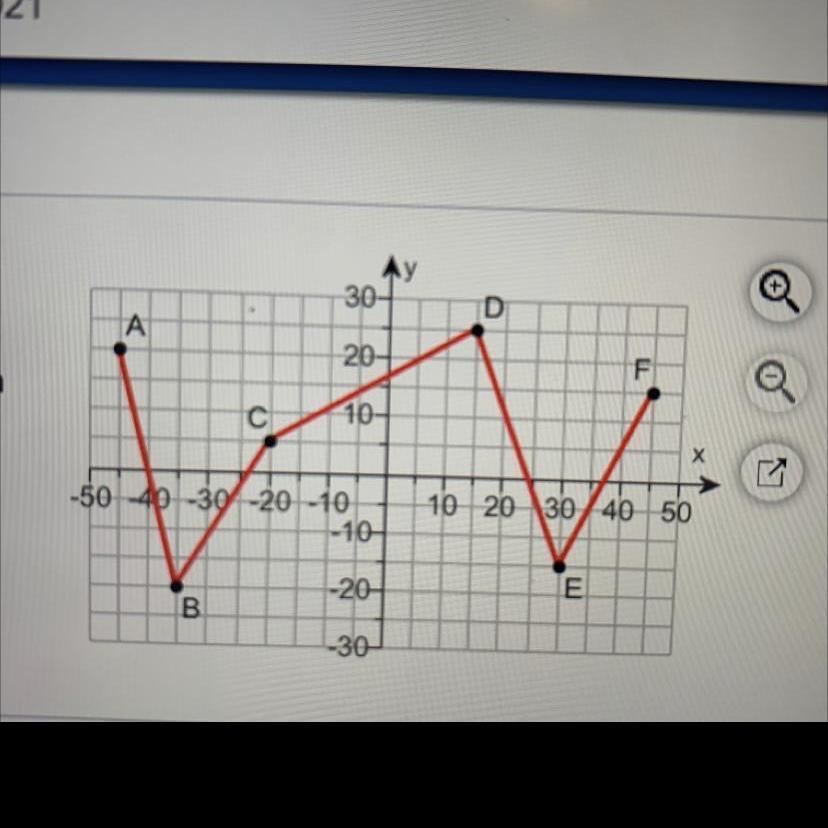
Answers
we know that
The distance between ywo points is giving by the formula
\(d=\sqrt{(y2-y1)^2+(x2-x1)^2}\)in this problem we need to calculate the distance between B and C
so
looking at the graph
B(-35,-20)=(x1,y1)
C(-20,5)=(x2,y2)
substitute in the formula
\(\begin{gathered} d=\sqrt{(5+20)^2+(-20+35)^2} \\ d=\sqrt{(25)^2+(15)^2} \\ d=\sqrt{850} \\ d=29.2\text{ m} \end{gathered}\)
The graph of a linear function is shown on the grid.
What is the rate of change of y with respect to x for this function?

Answers
Answer:
Step-by-step explanation:
Rate of change = (2-3.6)/(5-(-3)) = -1.6/8 = 0.2
-10+l 6+-17l - - 14 show how you got the answer
Answers
The solution to the expression -10 + |6 + -17| -- 14 is 15
How to evaluate the expression?The expression is given as:
-10+l 6+-17l - - 14
Rewrite properly as
-10 + |6 + -17| -- 14
Evaluate the sum and the difference
So, we have:
-10 + |6 + -17| -- 14 = -10 + |-11| + 14
Remove the absolute bracket
-10 + |6 + -17| -- 14 = -10 + 11 + 14
Evaluate the sum
-10 + |6 + -17| -- 14 = 15
Hence, the solution to the expression -10 + |6 + -17| -- 14 is 15
Read more about expressions at:
https://brainly.com/question/723406
#SPJ1
find the linear measure of an arc whose central angle is 144 on a circle of radius 35 inches
Answers
Answer:
The linear measure of an arc whose central angle is 144 on a circle of radius 35 inches is 28π inches or about 87.96 inches
Step-by-step explanation:
The linear measure of an arc is given by
\(s = 2\pi r(\alpha/360)\)
Where, α is the central angle (in degrees) of the arc
In our case,
r = 35 inches
α = 144 degrees
So, the linear measure would be,
\(s = 2\pi(35) (144/360)\\s = 28\pi \\\)
so s = 28π inches
or about 87.96 inches
Describe the shape of the distribution.
A. It is symmetric.
B. It is uniform.
C. It is bimodal.
D. It is skewed.

Answers
a card is drawn from a pack of 52 playing cards. find the probability that the card will be a jack, given that it is a face card.\
Answers
If a card is drawn from a pack of 52 playing cards, then the probability that the card will be jack is 1/13
Total number of playing cards in the pack = 52 cards
Number of jack cards in the pack = 4 cards
The probability is the ratio of the number of favorable outcomes to the total number of outcomes
The probability = Number of favorable outcomes / Total number of outcomes
Substitute the values in the equation
The probability that the card will be a jack = 4/52
Simplify the answer
= 1/ 13
Therefore, the probability that the card will be jack is 1/13
Learn more about probability here
brainly.com/question/11234923
#SPJ4
a ball is dropped form a height of 30 feet and rebounds 2/3 of the distance it falls on each bounce. how far has the ball traveled vertically when it stops?
Answers
When the ball stops bouncing, it will have traveled a total vertical distance of 90 feet.
To determine how far the ball has traveled vertically when it stops, we can calculate the sum of the geometric series formed by the distances of each bounce.
Given that the ball rebounds 2/3 of the distance it falls, the distances covered by each bounce form a geometric sequence with a common ratio of 2/3.
The distance the ball initially falls is 30 feet. The subsequent distances covered by each bounce can be calculated as follows:
First bounce: 30 * (2/3) = 20 feet
Second bounce: 20 * (2/3) = 40/3 feet
Third bounce: (40/3) * (2/3) = 80/9 feet
Fourth bounce: (80/9) * (2/3) = 160/27 feet
Fifth bounce: (160/27) * (2/3) = 320/81 feet
And so on...
To calculate the total distance covered, we sum up the infinite geometric series:
Sum = a / (1 - r)
where "a" is the initial term (30 feet) and "r" is the common ratio (2/3).
Sum = (30) / (1 - 2/3)
Sum = (30) / (1/3)
Sum = 90 feet
Therefore, when the ball stops bouncing, it will have traveled a total vertical distance of 90 feet.
To learn more about ratio visit;
https://brainly.com/question/13419413
#SPJ11
This is math Will show more photos to help u out



Answers
A compound statement is a group of two or more statements connected using words such as 'or', 'and', 'if then', 'if and only if'.
Then, we have:
Part a)This is a compound statement of conditional type where the first simple statement is the condition for the second simple statement.
Then, we have:
p: The dog is hungry.
q: She is barking.
p→q: The dog is hungry if she is barking.
Thus, this statement is a compound statement of conditional type.
Part b)We can see this statement as a conjunction of two simple statements:
• p: Bill reads books.
,• q: Bill reads magazines.
Then, we have:
p ∧ q: Bill reads books and magazines.
Thus, this statement is a compound statement of conjunction type.
Part c)We can see this statement as a conjunction of two simple statements:
• p: There are wild animals on G Ranch.
,• q: There are wild animals on L Ranch.
Then, we have:
p ∧ q: There are wild animals on G and L Ranch.
Thus, this statement is a compound statement of conjunction type.
AnswerPart a) Compound statement of conditional type.
Part b) Compound statement of conjunction type.
Part c) Compound statement of conjunction type.
Find the area of the irregular figure.
4 in.
6 in.
A = [? ]in.²
10 in.
7 in.
11 in.
6 in.
![Find the area of the irregular figure.4 in.6 in.A = [? ]in.10 in.7 in.11 in.6 in.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/Z24cvEbs0ZdqvS9YT6KbMu49ztVRfEJr.png)
Answers
Answer:
160 square inches
Step-by-step explanation:
You can split the irregular figure up into regular shapes:
the top 4x6 inch rectangle
the middle section can be a 18x6 rectangle (added 7+11 for the length)
the bottom 4x7 rectangle (sibtracted 10-6 for the width)
Then, find the area of each section with the equation A = lw.
A= 4(6) = 24 square inches
A = 18(6) = 108 square inches
A = 4(7) = 28 square inches
Add these areas up to get the total area of the irregular figure.
24 + 108 + 28 = 160 square inches
Instead of having a cake, Paul wants to make ice cream sundaes at his next birthday party. He thinks each person will eat 2 cups of ice cream, and there will be 24 people at his party. How many 1-gallon tubs of ice cream should he buy?
Answers
Answer:
8
Step-by-step explanation:
24÷2=16×1=16÷2=8
am not sure I think the answer is also 16 so look at other people answer
Paul should buy 3 gallons
How to calculate unit price of something?Unit means 'single entity', the fundamental constructing block. Usually, it is 1 in mathematics and science.
Thus, unit price of something is price of 1 thing.
Thus, suppose we're taking about price of mangoes, then unit price will denote the price of 1 mango.
There are 16 cups in a gallon, and if each person will eat 2 cups, and there are 24 people, multiply 24 by 2 to get the number of cups.
24 x 2 = 48.
Then, divide that by 16 (the number of cups in a gallon) to how many gallons.
48 ÷ 16 = 3
Therefore, he needs 3 gallons.
Learn more about unit price here:
https://brainly.com/question/945712
#SPJ2
The components of the displacement vector (u) at a point (X1,X2,X3), with respect to (x,y,z) coordinate system, are given as ux=A{21a2X2+(21X12−lX1)X2−41(X23+X2X32)}uy=A{21a2X1+21lX12−61X13+41(l−X1)(X22−X32)}uz=A{21(l−X1)X2X3} Where (a,A) and (l) are constants. 1- Find the components of the displacement gradient tensor (∇u). 2- Find the components of the linear strain tensor (∇ε) 3- Evaluate the strain components at a point (P) whose coordinates with respect to (x,y,z) are (2l,2a,2a) 4- At the point (P) find the strain along the direction n=31[111]⊤ 5- Again at the point (P) Find the shear strain associated with the directions n1=51[3−40]⊤n2=51[430]⊤
Answers
The components of the displacement gradient tensor (∇u), linear strain tensor (∇ε), strain components at point P(2l, 2a, 2a), strain along direction n = [1, 1, 1]⁺, and shear strains along directions n1 = [3, -4, 0]⁺ and n2 = [4, 3, 0]⁺ at point P can be determined using the given expressions and coordinates.
The components of the displacement gradient tensor (∇u) can be found by taking the partial derivatives of the displacement vector (u) with respect to the coordinate variables (x, y, z):
(∂u/∂x) = (2A/1) {a^2X2 + (X1^2 - X1)X2 - (X3^2 + X2X3)}
(∂u/∂y) = (2A/1) {a^2X1 + (X1^2 - 1)X2 - (X1^3 + X2X3)}
(∂u/∂z) = (2A/1) {(1 - X1)X2X3}
The components of the linear strain tensor (∇ε) can be obtained from the components of the displacement gradient tensor (∇u) using the formula:
(∂εij/∂xi) = (1/2) * [(∂u_j/∂xi) + (∂u_i/∂xj)]
To evaluate the strain components at point P(2l, 2a, 2a), substitute these coordinates into the expressions derived in step 2.
To find the strain along the direction n = [1, 1, 1]⁺, calculate the dot product of n with the strain tensor (∇ε):
Strain along n = n · ∇ε · n = ε11 + ε22 + ε33
To find the shear strain associated with the directions n1 = [3, -4, 0]⁺ and n2 = [4, 3, 0]⁺ at point P, calculate the dot product of n1 and n2 with the shear strain tensor (∇γ):
Shear strain along n1 = n1 · ∇γ · n1 = γ11 + γ22 + 2γ12
Shear strain along n2 = n2 · ∇γ · n2 = γ11 + γ22 + 2γ12
Evaluate the expressions using the derived components from step 2 at point P to find the desired strain values.
Learn more about partial derivatives from the given link:
https://brainly.com/question/28751547
#SPJ11
The following cone has a slant height of 17
cm and a radius of 8
cm.
What is the volume of the cone?
Responses
480π
320π
544π
Answers
The formula for the volume of a cone is:
V = (1/3)πr²h
where r is the radius of the base, h is the height of the cone, and π is pi.
In this case, the slant height is given as 17 cm, which we can use with the radius to find the height of the cone using the Pythagorean theorem:
h² = s² - r²
h² = 17² - 8²
h² = 225
h = 15
Now that we have the height, we can plug in the values for r and h into the formula for the volume:
V = (1/3)π(8²)(15)
V = (1/3)π(64)(15)
V = (1/3)(960π)
V = 320π
Therefore, the volume of the cone is 320π cubic cm. Answer: 320π.
the radius of the base of a cylinder is 10 centimeters, and urs height is 20 centimeters. a cone is used to fill the cylinder with water. the radius of the cone base is 5 centimeters, and it’s height is 10 centimeters the number of times one needs to use the completely fillies cone to completely fill the cylinder with water is
Answers
Answer:
The answer is 24 times
find the slope of the following ^ :))
|

Answers
Answer:
m [slope] = 0
Step-by-step explanation:
When the slope is 0, x cancels out so the y value will remain the same.
There are several methods to finding slope but the easiest way to do this is by dividing the second y value - first y value by the second x value - first x value.
m = ∆y/∆x = y2-y1/x2-x1
You y2 and x2 are interchangable with y and x, because y1, and x1 are part of the starting coordinate,.
The reason you subtract the second
value from the first is because in a directly proportional relationship, y increases as x increases so the next x values will have a greater y value, this is a measure of steepness.
So the slope is:
-1 - -1 / 3 - -2 = -1 + 1 / 3 + 2 = 0 / 5 = 0.
Answer:
heres what u need
Step-by-step explanation:
\(\frac{-1}{-2} \frac{-1}{3}\)
divide top from bottom
\(-2/-1=2\)
2 is your x
\(3/-1=-3\)
-3 is your y
so your slope is (2,-3)
(PLS HELP!!!)
The medians of ADEF are DK, EL, and FJ. They meet at a single point M.
(In other words, M is the centroid of ADEF.)
Suppose EL=24, DM = 12, and FM = 6.
Find the following lengths.
Note that the figure is not drawn to scale.
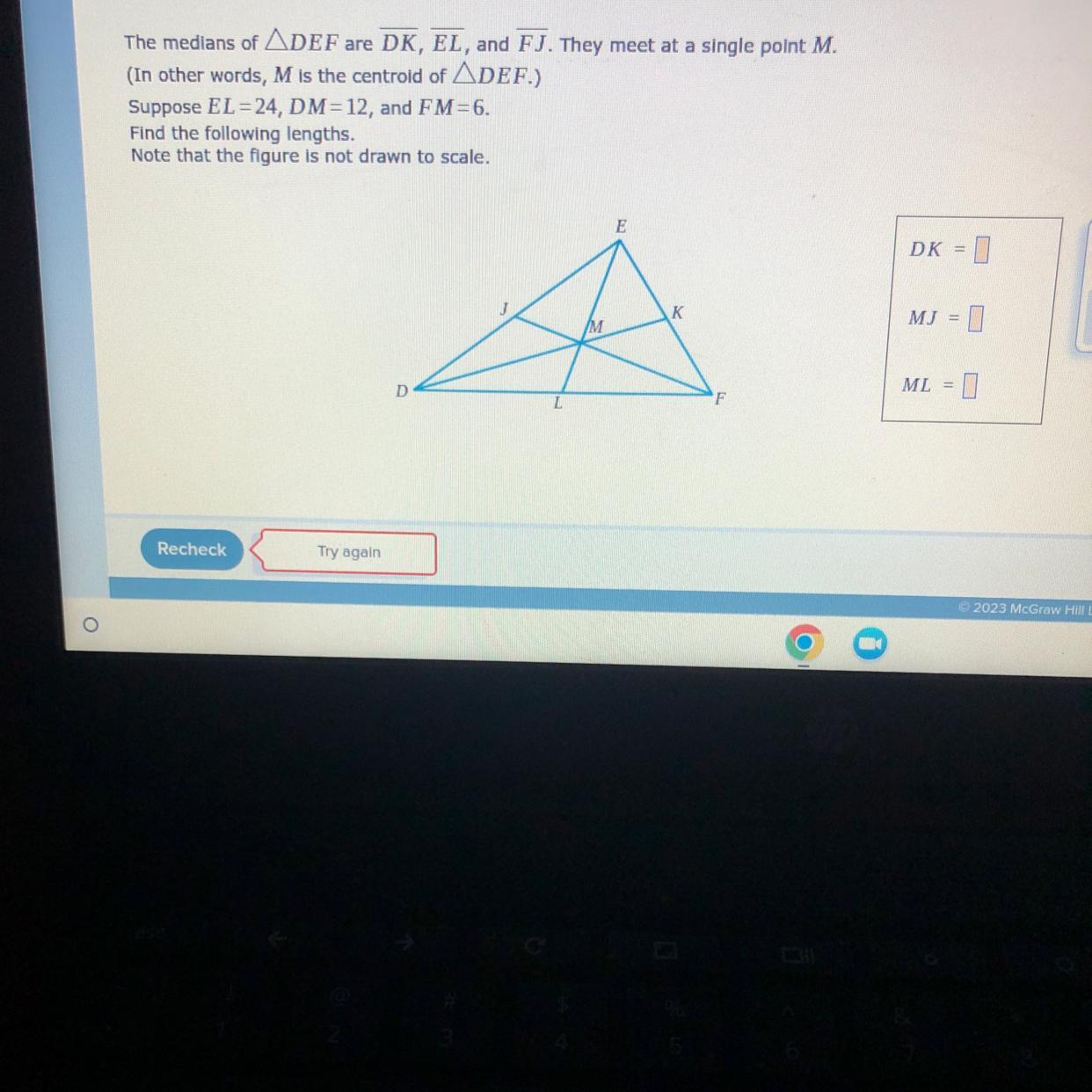
Answers
Answer:
DK = 18
MJ = 3
ML = 8
Step-by-step explanation:
In this problem, we need to use the Median of a Triangle Formula. This formula states that EM/EL = FM/JF = DM/DK = 2/3. To implement this into our question, we can write ML/EL = 1/3, so we get that ML = 24/3 = 8. We also know that MJ/FM = 1/2, so MJ = 6/2 = 3. Finally, DM/DK = 2/3, so DK = (12*3)/2 = 18. Hope this is correct.
Sandy and Patrick want to meet in the middle of their two homes for a picnic lunch. If we imagine their homes on a coordinate grid, where every unit is 1 foot, decide at what coordinate point they should meet for lunch. Patrick lives at (-4,-12) and Sandy lives at (3,16)
Answers
Answer: (-4,16)
Step-by-step explanation:
Evaluate 68 % of 948.37 m Give your answer rounded to 2 DP.
Answers
Answer:
644.89
Step-by-step explanation:
Answer:
644.89 m
Step-by-step explanation:
68 / 100 * 948.37 = 0.68 * 948.37 = 644.89 m (2 d.p.)
1 2 3 4 5 6 7 8 9 10 The probability that a randomly selected point on the grid below is in the blue area is StartFraction 9 over 16 EndFraction. A grid with 16 squares. 9 squares are shaded blue. Which expression can be used to find the probability that a randomly selected point is in the white area of the grid?
Answers
Using it's concept, the expression that can be used to find the probability that a randomly selected point is in the white area of the grid is:
\(\frac{7}{16}\)
What is a probability?A probability is given by the number of desired outcomes divided by the number of total outcomes.
Researching the problem on the internet, 7 out of 16 squares are in the white area, hence the probability is given by:
\(p = \frac{7}{16}\).
More can be learned about probabilities at https://brainly.com/question/24372153
#SPJ1
What is the slope of the line that passes through the points (7,-4)
and (11,-4)? Write your answer in simplest form.
Answers
Slope of line=0
Slope of line=\(\frac{y2-y1}{x2-x1}\)
=\(\frac{-4+4}{11-7}\) =\(\frac{0}{4}\) =0
In mathematics, a line's slope, also known as its gradient, is a numerical representation of the line's steepness and direction. The letter m is frequently used to represent slope; the reason for this usage is unclear, but it can be found in O'Brien's (1844) and Todhunter's (1888) formulations of the equation for a straight line as "y = mx + b" and "y = mx + c," respectively.
The ratio of the "vertical change" to the "horizontal change" between (any) two unique points on a line is used to compute the slope.A declining line has a negative "rise." The line might be useful, as determined by a road surveyor, or it might appear in a diagram that represents a road or a roof as a description or a design.
The slope's absolute value serves as a gauge for a line's steepness, incline, or grade. A steeper line is indicated by a slope with a higher absolute value. A line can be drawn in one of four directions: upward, downward, horizontal, or vertical.
To learn more about Slope of line form the given link:
https://brainly.com/question/16180119
#SPJ9
u decreased by 17 equals what
Answers
Step-by-step explanation:
u decreased by 17 equals
= u-17
Answer:
u-17
Step-by-step explanation:
Solve inequalities and I'll do the graphing

Answers
15. x>7 Some of them are unslovable
16. n≥−5
17. G>5
18. k≤1
19.−2<b≤6
20. −8<m<−3
21. unslovable
22. −9<x<4
23. unslovable
24. m<−9 or m>9
Answer:
work is shown and pictured


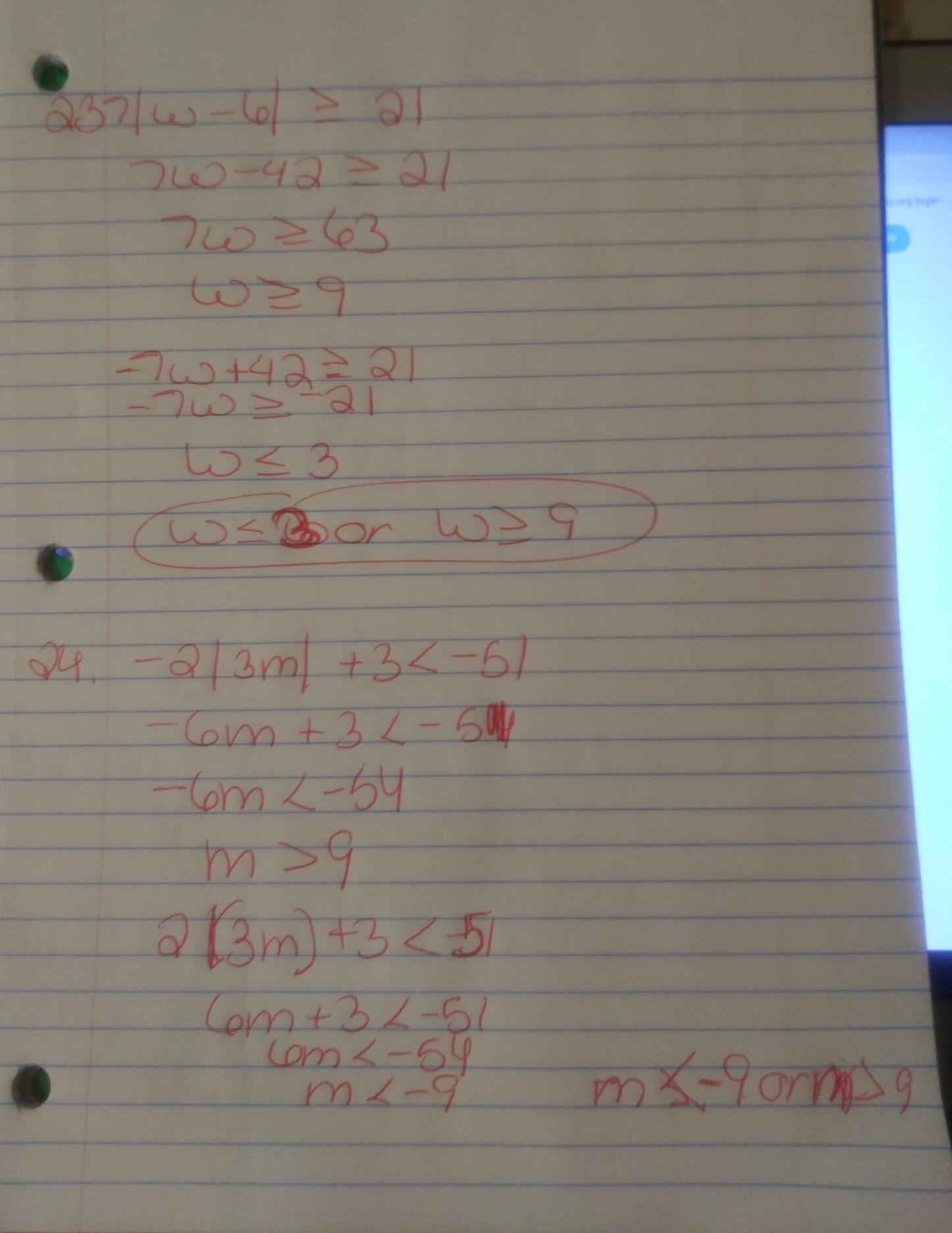
Consider the function f(x) whose second derivative is f(x)=9x+6sin(x). If f'(0)=4 and f(0)=3, what is f(4)?
Please do not include the constant (+C) in your answer.
Answers
The value of function f(4) is 323/3 - 2sin(4).
Given, f''(x) = 9x + 6sin(x)and f'(0) = 4, f(0) = 3
The first derivative of f(x) can be obtained by integrating f''(x).f'(x) = ∫ f''(x)dx = 4.5x² - 6cos(x) + C1
Applying initial condition f'(0) = 4,f'(0) = 4.5(0)² - 6cos(0) + C1= 4=> C1 = 10/3
Thus, f'(x) = 4.5x² - 6cos(x) + 10/3The function f(x) can be obtained by integrating f'(x).f(x) = ∫ f'(x)dx= 1.5x³ - 6sin(x) + (10/3)x + C2
Applying initial condition f(0) = 3,f(0) = 1.5(0)³ - 6sin(0) + (10/3)(0) + C2= 3=> C2 = 3
Thus, f(x) = 1.5x³ - 6sin(x) + (10/3)x + 3
Now, we have to find f(4)f(4) = 1.5(4)³ - 6sin(4) + (10/3)(4) + 3= 94 - 6sin(4) + (40/3) + 3= 323/3 - 2sin(4)
To know more about derivative click on below link:
brainly.com/question/29144258#
#SPJ11
At lunchtime, the temperature was 14°F. By 9 p.m., the temperature had dropped 18 degrees. What was the temperature, in degrees Fahrenheit, at 9 p.m.?
Answers
Answer:
-4 degrees
Step-by-step explanation:
You subtract 14-18