The total time, measured in units of 100 hours, that a teenager runs her hair dryer over a period of one year is a continuous random variable X that has the density function
f(x)= x, 0
f(x) = 2 – x, 1 ≤ x < 2
f(x) = 0, elsewhere
evaluate the mean of the random variable , where Y is equal to the number of kilowatt hours expended annually
Answers
The expected value of PX is 2.Therefore(Y) = E(PX) / 100= 2 / 100= 0.02The mean of the random variable Y, where Y is equal to the number of kilowatt hours expended annually is 0.02. Therefore, the correct option is (D) 0.02.
Why The expected value of PX is 2?
The given problem states that the total time, measured in units of 100 hours, that a teenager runs her hair dryer over a period of one year is a continuous random variable X that has the density function f(x)=x, 0 < x < 1, f(x) = 2 – x, 1 ≤ x < 2 and f(x) = 0, elsewhere. We need to evaluate the mean of the random variable where Y is equal to the number of kilowatt hours expended annually.
The total time, measured in units of 100 hours, that a teenager runs her hair dryer over a period of one year is given as X. Let us calculate the expected value of the random variable Y which is equal to the number of kilowatt hours expended annually.The number of kilowatt hours expended annually Y is calculated as follows:Y = Power consumed × Hours of use per yearLet Power consumed = P and Hours of use per year = X × 100.The number of kilowatt hours expended annually Y is equal to the product of the power consumed and hours of use per year.
Therefore, we haveY = PX × 100 = (P/100) XThe expected value of Y is given byE(Y) = E(PX) / 100where E(PX) is the expected value of PX.So, we have to calculate E(PX).The expected value of PX is given bye(PX) = ∫ xf(x) dx (0 to 1) + ∫ xf(x) dx (1 to 2) (as given)Now, substituting the given function in the above formula we getE(PX) = ∫ x² dx (0 to 1) + ∫ 2x - x² dx (1 to 2)E(PX) = [x³/3] (0 to 1) + [(x² - x³/3)] (1 to 2)E(PX) = 2/3 + 4/3 = 2
The expected value of PX is 2.Therefore,E(Y) = E(PX) / 100= 2 / 100= 0.02The mean of the random variable Y, where Y is equal to the number of kilowatt hours expended annually is 0.02. Therefore, the correct option is (D) 0.02.
Learn more about PX.
brainly.com/question/30976942
#SPJ11
Related Questions
to can be driven before it would need to be junked is an exponential random variable with parameter smith has a used car that he claims has been driven only 10,000 miles. if jones purchases the car, what is the
Answers
Answer:
2334
Step-by-step explanation:
Solve the differential equation
Y"-9y=9x/e^3x
by way of variation of parameters.
Answers
Using variation of parameters, the solution to the non-homogeneous differential equation is;
\(y(x) = y_h_(_x_) + y_p_(_x_)\\y(x) = c_1e^(^3^x^) + c_2e^(^-^3^x^) + (-3x - c_3/6 + c_4e^(^3^x^))e^(^-^3^x^).\)
What is the solution of the differential equation?To solve the differential equation y" - 9y = 9x/e³ˣ using the method of variation of parameters, we first find the solution to the associated homogeneous equation y" - 9y = 0.
The characteristic equation is r² - 9 = 0.
Factoring the equation, we have (r - 3)(r + 3) = 0.
This gives us two distinct real roots: r = 3 and r = -3.
Therefore, the general solution to the homogeneous equation is:
y_h(x) = c₁e³ˣ + c₂e⁻³ˣ, where c₁ and c₂ are arbitrary constants.
Next, we assume a particular solution of the form:
y_p(x) = u₁(x)e³ˣ + u₂(x)e⁻³ˣ
To find the values of u₁(x) and u₂(x), we substitute Yp(x) into the original differential equation:
[(u₁''(x)e³ˣ + 6u₁'(x)e³ˣ + 9u₁(x)e³ˣ - 9(u₁(x)e³ˣ + u₂(x)e⁻³ˣ)] - 9[u₁(x)e³ˣ + u2(x)e⁻³ˣ] = 9x/e³ˣ
Simplifying, we get:
u₁''(x)e³ˣ + 6u₁'(x)e³ˣ - 9u₂(x)e^⁻³ˣ = 9x/e³ˣ
To solve for u1'(x) and u2'(x), we equate coefficients of like terms:
u₁''(x)e³ˣ + 6u₁'(x)e³ˣ = 9x/e³ˣ ...eq(1)
-9u2(x)e⁻³ˣ = 0 ...eq(2)
From equation (2), we can see that u₂(x) = 0.
Now, let's differentiate equation (1) with respect to x to find u₁''(x):
u₁''(x) + 6u₁'(x) = 9/e³ˣ.
This is a first-order linear differential equation for u₁'(x). We can solve it by using an integrating factor. The integrating factor is given by;
\(e^(^\int^6 ^d^x^) = e^(^6^x^).\)
Multiplying both sides of the equation by e⁶ˣ, we have:
\(e^(^6^x^)u_1''(x) + 6e^(^6^x^)u_1'(x) = 9e^(^3^x^)/e^(^3^x^).\)
Simplifying further, we get:
\((u_1'(x)e^(^6^x^)^)' = 9.\)
Integrating both sides with respect to x, we have:
u₁'(x)e⁶ˣ = 9x + c₃, where c₃ is the integration constant.
Now, we solve for u₁'(x):
\(u_1'(x) = (9x + c3)e^(^-^6^x^).\)
Integrating u1'(x) with respect to x, we get:
u₁(x) = ∫[(9x + c3)e⁻⁶ˣ] dx.
Integrating by parts, we have:
u₁(x) = (-3x - c3/6)e⁻⁶ˣ + c₄, where c4 is the integration constant.
Therefore, the particular solution is:
Yp(x) = u₁(x)e³ˣ + u₂(x)e⁻³ˣ
\(y_p_(_x_)= [(-3x - c_3/6)e^(^-^6^x) + c_4]e^(^3^x^)\\y_p_(_x_) = (-3x - c_3/6 + c_4e^(^3^x^))e^(^-^3^x^).\)
The general solution to the non-homogeneous differential equation is the sum of the homogeneous solution and the particular solution:
\(y(x) = y_h_(_x_) + y_p_(_x_)\\y(x) = c_1e^(^3^x^) + c_2e^(^-^3^x^) + (-3x - c_3/6 + c_4e^(^3^x^))e^(^-^3^x^).\)
Thus, we have obtained the solution to the differential equation using the method of variation of parameters.
learn more on differential equation here;
https://brainly.com/question/1164377
#SPJ4
Multiply or divide, write your answer in scientific notation.
1.44 over 2.4 × 10^10 over 10^2 =
Can you help me with this problem?
Answers
= 6 • 10^7 in scientific notation
Answer: 6x10^-13 (Reminder the ^ mark usually means the number next to it is a exponent!)
Step-by-step explanation:
Move the decimal so there is one non-zero digit to the left of the decimal point. The number of decimal places you move will be the exponent on the
10
. The sign of the exponent will depend on the direction you are moving the decimal
The probability that a baseball player will get a hit is 0.300. What is the probability that he will get one hit in his next two turns at bat
Answers
Answer:
0.42.
Step-by-step explanation:
Probability of a miss on one bat = 1 - 0.3 = 0.7.
There are 2 scenarios:
First bat a Hit, Second bat a Miss, or
First bat a Miss, Second bat a Hit.
First scenario: Probability = 0.3 * 0.7 = 0.21.
Second is 0.7 * 0.3 = 0.21.
So the answer is 0.21 + 0.21 = 0.42.
Nicole Is A Lifeguard And Spots A Drowning Child 40 Meters Along The Shore And 60 Meters From The Shore To The Child. Nicole
Answers
The sum of the times for swimming to the child and swimming back should be less than or equal to 120 seconds:
**60 / (v_swim + v_current) + 40 / (v_swim - v_current) ≤ 120**
To reach the drowning child, Nicole needs to swim a distance of 60 meters directly from the shore to the child, while also accounting for the current that pulls her downstream.
Let's denote the speed at which Nicole can swim in still water as **v_swim** (in meters per second) and the speed of the current as **v_current** (in meters per second).
The time it takes for Nicole to swim from the shore to the child can be calculated using the formula:
**Time = Distance / Speed**
The distance Nicole needs to swim is 60 meters, and her swimming speed is the sum of her swimming speed in still water and the speed of the current, so we have:
**Time = 60 / (v_swim + v_current)**
Similarly, to swim back to the shore, Nicole needs to cover a distance of 40 meters, so the time it takes for her to swim back is:
**Time = 40 / (v_swim - v_current)**
Since Nicole has 2 minutes (or 120 seconds) before the child is in danger, the total time she spends swimming should not exceed this limit. Therefore, the sum of the times for swimming to the child and swimming back should be less than or equal to 120 seconds:
**60 / (v_swim + v_current) + 40 / (v_swim - v_current) ≤ 120**
This equation represents the time constraint that Nicole must satisfy.
To find the minimum swimming speed required for Nicole to reach the child in time, we need to solve this equation for **v_swim**. However, without specific information about the speed of the current or any other variables, it is not possible to determine the exact value of **v_swim**.
If you can provide additional information or clarify any missing details, I can assist you further in solving the equation.
Learn more about sum here
https://brainly.com/question/24205483
#SPJ11
In the diagram, the measures of 22, 23 and 26 are 40°. The measure of 21
is 140°. Are lines cand d parallel?

Answers
Answer:
c. Yes because ∠2 and ∠6 are congruent.
Step-by-step explanation:
From the picture attached,
m(∠2) = m(∠3) = m(∠6) = 40°
m(∠1) = 140°
Since (∠2 ≅ ∠6) (corresponding angles)
Therefore, by the converse theorem of corresponding angles lines c and d are parallel.
Option c is the answer.
help me........... .
Answers
Answer:
I do not see the question.
Step-by-step explanation:
9) Brenn has $60 in his savings account. His brother Chris has $135 in his. Brenn decides to save $5 of his allowance each week, while Chris decides to spend his whole allowance along with $10 of his savings each week. After how many weeks will Brenn and Chris have the same amount of money in their savings accounts?
Answers
Answer:
9) 15
Step-by-step explanation:
Simplify (15y+x)+45y and show steps
Answers
Answer:
\((15y + x) + 45y \\ = 15y + x + 45y \\ = 15y + 45y + x \\ = 60y + x\)
Answer:
60y + x
Step-by-step explanation:
(15y + x) + 45y
15y + x + 45y
60y + x
for 20 points and brainliest

Answers
Answer:
(-3)^10
Step-by-step explanation:
Answer:
I would say the second one srry if I’m wrong
Step-by-step explanation:
URGENT PLEASE HELP!
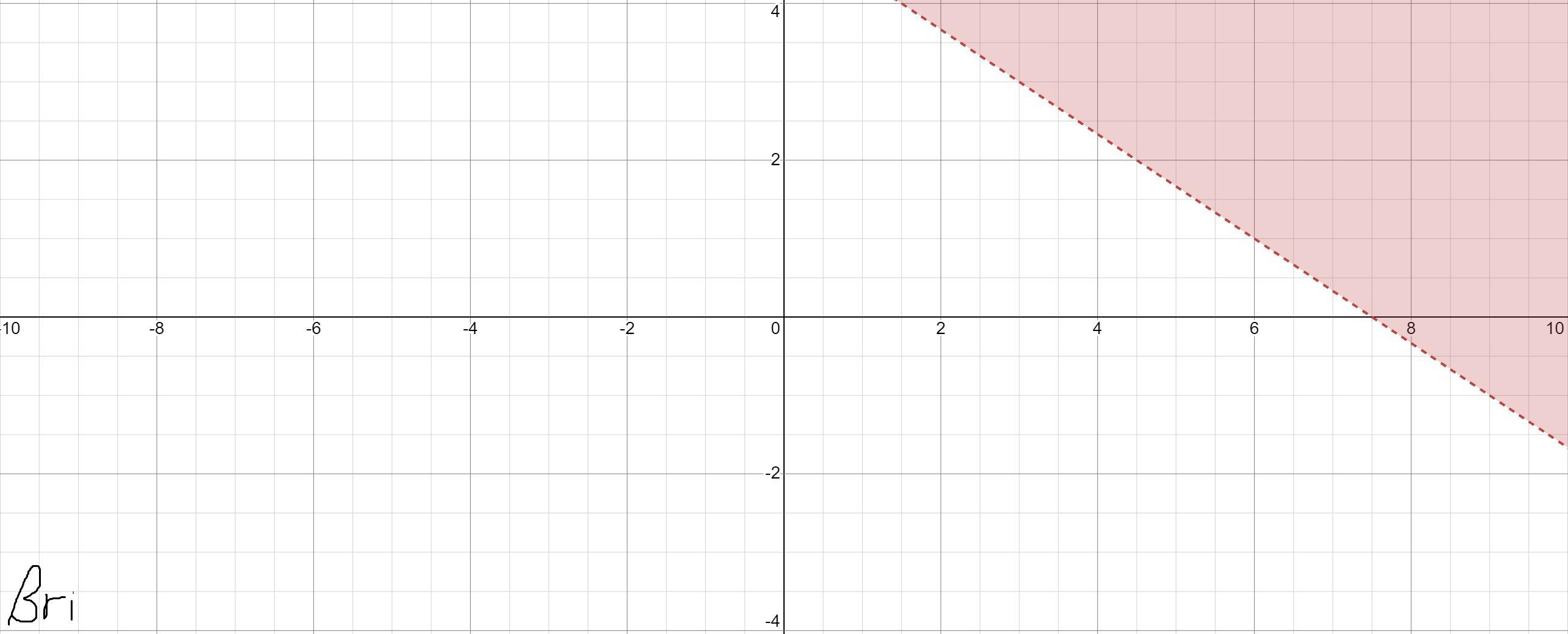
Explain the steps you would take to graph 2x-3y>15.
Answers
Answer:
y>5−2x/3
Step-by-step explanation:
Round the number to 3
significant figures.
0.2590100

Answers
Answer:
0.259
Step-by-step explanation:
There are some rules in determining what numbers are significant figures.
All non-zero numbers are significant.Zeroes between two non-zero numbers are significant.Zeroes at the front of a number are not significant.Trailing zeroes are only significant if there is a decimal point.We can determine how many significant figures the number currently has.
The first zero is not significant.2, 5, 9, and 1 are significant because they are non-zero numbers.The zero between 9 and 1 is significant because it is a captive zero.The zeroes at the end of the number are significant because they are trailing zeroes.There are currently seven significant figures. In order to round the number to three significant figures, we must round it to the thousandths place, or the 9.
The rounding rules are:
If the digit in the place after the number we are rounding is less than 5, you round down (or in other words, keep the number the same; Ex: 74 becomes 70)If that digit is greater than 5, you round up (Ex: 78 becomes 80)Since 0 is less than 5, the number rounded to 3 significant figures is 0.259.
Write an equation for this model and solve for `x`

Answers
x = -0.8
which of the following statistics determines whether there are differences between two nominally scaled variables?
Answers
The chi-square statistic is used to determine whether there are differences between two nominally scaled variables. Chi-Square is a statistical test used to compare two nominal variables to determine whether they differ.
The Chi-Square test is used to test for differences between two groups. When you want to compare groups or examine the relationship between two variables, this test is useful. The chi-square test is a method of statistical inference that can be used to compare observed frequencies with expected frequencies, allowing us to determine whether there is a meaningful difference between them. When the p-value obtained from a chi-square test is less than 0.05, it is generally considered statistically significant.
Learn more about Chi-Square
https://brainly.com/question/32595988
#SPJ11
5(2c-3) = 3(3c - 5)
Answer Choices:
No solution
c = -15
c = 0
Infinitely many solutions
Answers
Answer: C=0
Step-by-step explanation:
expand \(5\left(2c-3\right)\) : \(10c-15\)
expand \(3\left(3c\:-\:5\right)\) : \(9c-15\)
\(10c-15=9c-15\)
add 15 on both sides
\(10c-15+15=9c-15+15\)
simplify
\(10c=9c\)
\(\mathrm{Subtract\:}9c\mathrm{\:from\:both\:sides}\)
\(10c-9c=9c-9c\)
simplify
\(c=0\\\)
Answer:
C=0
Step-by-step explanation:
Hope it helps.
From MATH workbook.

Answers
Answer:
C. -8
Step-by-step explanation:
-2^4 = 16
-2^-1 = -1/2
Answer:
-8
Step-by-step explanation:
Ok so lets first solve the first one:
\(-2^{4} = -2 x -2 x -2 x-2=\) \(16\)
\(x\) represents times if that's confusing.
Ok so I got \(16\) b/c if we multiply a negative times a negative we get positive. And there are 4 negatives not 3 not not 5 but 4 so we get positive.
Now second one:
\(-2^{-1} = - 0.5\)
Now lets put it together!
\(-0.5 x 16=-8\)
Hope this helps :)
In parallelogram lonm, what is om? 7 cm 17 cm 24 cm 34 cm
Answers
In parallelogram lonm, om is 34.
What is parallelogram?
A parallelogram is a straightforward quadrilateral with two sets of parallel sides in Euclidean geometry. A parallelogram's facing or opposing sides are of equal length, and its opposing angles are of equal size.
A quadrilateral with the opposing sides parallel is called a parallelogram. A parallelogram with all right angles is known as a rectangle, and a quadrilateral with equal sides is known as a rhombus.
First we have OQ =QM,
So 2x+3=3x-4,
x =7.
Hence OM =2(17)=34.
To learn more about quadrilateral visit:https://brainly.com/question/13805601
#SPJ4
Answer: D) 34
Step-by-step explanation:
edge 2023
Find the slope of the line that passes through (2, 7) and (-4, 19).
m =
Answers
The slope, m, of the line that passes through (2, 7) and (-4, 19) is -2.
According to the question,
We have the following information:
A line is passing through two points (2,7) and (-4,19).
We know that the slope of the line is denoted by m and the following formula is used to find the slope of the line passing through two points:
m = (y2-y1)/(x2-x1)
(More to know: we can also easily find the equation of the line using the slope given and the points from which the line is passing.)
In this case, we have x1 = 2, y1 = 7, x2 = -4 and y2 = 19.
m = (19-7)/(-4-2)
m = 12/(-6)
m = -2
Hence, the slope, m, of the line that passes through (2, 7) and (-4, 19) is -2.
To know more about slope here
https://brainly.com/question/16180119
#SPJ1
which of the following constructions can be accomplished with paper folding? Check all that apply

Answers
Answer:
The correct options are;
A, B, and D
Step-by-step explanation:
Geometry that can be completed with paper folding construction includes;
1) Constructing of a line perpendicular to another line through a point
2) Constructing a triangle from a vertex which is the altitude
3) Constructing a parallel line to a line through a given point
4) Construct bisector of an angle
5) Locating the in-center of a triangle
Therefore, the correct options are A, B, and D
Answer:
abd
Step-by-step explanation:
Please help me with this qurstion

Answers
Answer:
The value of \(x\) is \(19\).
Angle R's measure is \(43^{\circ}\).
Angle S' measure is \(20^{\circ}\).
Angle T's measure is \(117^{\circ}\).
Step-by-step explanation:
Step 1: Construct expressions for the angles in terms of x
The angle R is said to be five more than twice x, which means that 5 is added to 2x:
\(\text{R}=5+2x\)
The angle S is said to be one more than x, which means that 1 is added to x:
\(\text{S}=1+x\)
The angle T is said to be sixteen less than seven times x, which means that 16 is subtracted from 7x:
\(\text{T}=7x-16\)
Step 2: Create an equation with all the expressions
Since there are three angles in the shape, it is clearly a triangle.
The sum of angles of a triangle is \(180^{\circ}\).
Which means that the sum of the expressions above, would equal to \(180\):
\((5+2x)+(1+x)+(7x-16)=180\)
Step 3: Solve the equation
The equation is:
\((5+2x)+(1+x)+(7x-16)=180\)
Upon solving it, we get:
\((5+2x)+(1+x)+(7x-16)=180\\\\\text{Remove the brackets:}\\5+2x+1+x+7x-16=180\\\\\text{Add the like terms:}\\10x-10=180\\\\\text{Add 10 on both sides of the equation:}\\10x-10+10=180+10\\\\\text{Simplify:}\\10x=190\\\\\text{Divide by 10 on both sides of the equation:}\\\frac{10x}{10}=\frac{190}{10}\\\\\text{Simplify:}\\x=19\)
Step 4: Calculate the measure of the angles
With \(x=19\), substitute and calculate the angle R:
\(\text{R}=5+2x\\\text{R}=5+2(19)\\\\\text{Calculate:}\\R=43^{\circ}\)
Calculate the angle S:
\(\text{S}=1+x\\\text{S}=1+19\\\\\text{Calculate:}\\\text{S}=20^{\circ}\)
Calculate the angle T:
\(\text{T}=7x-16\\\text{T}=7(19)-16\\\\\text{Calculate:}\\\text{T}=117^{\circ}\)
Fully factor the following polynomials. Explain your thought process with your solution.
a. ????(x) = 2x3 − 25x2 + 53x − 30 [3 marks]
b. ????(x) = x3 + 3x − 4 [3 marks]
Answers
a. the factors of equation is \(f(x)=(x-1)(x-10)(2x-3)\)
b. the factors of equation is \(f(x)=(x-1)(x^2+x+4)\)
Define the term polynomial?A polynomial is an expression consisting of variables and coefficients that involves only the operations of addition, subtraction, and multiplication, with non-negative integer exponents.
a. Given function,
\(f(x)=2x^3 -25x^2 + 53x - 30\)
By using trial and error method, put values of x =1, x= 10, and x= 3/2 are satisfied values for above function,
\(f(x)=(x-1)(x-10)(2x-3)\)
therefore, the factors of equation is (x-1) (x-10) (2x-3)
b. Given function,
\(f(x)=x^3 +3x - 4\)
Similarly using trial and error method,
\(f(x)=(x-1)(x^2+x+4)\)
therefore, the factors of equation is (x-1) (x² + x + 4)
To know more about expression, visit:
https://brainly.com/question/1859113
#SPJ1
Factor of given polynomials are a. (x-1)(x-10)(2x-3), b. (x-1)(x² + x + 4) .
Describe polynomials ?In mathematics, a polynomial is an expression that consists of variables and coefficients, combined using the operations of addition, subtraction, and multiplication, but not division by a variable. The variables in a polynomial can only have non-negative integer exponents.
Polynomials can have different degrees, which is the highest power of the variable in the expression. For example, the polynomial 3x² - 5x + 2 is a quadratic polynomial, since its highest power of x is 2. If the degree of a polynomial is n, then it has at most n roots, which are the values of x that make the polynomial equal to zero.
Polynomials are used in many areas of mathematics and science, including algebra, calculus, physics, and engineering. They are used to model and analyze many different types of phenomena, such as motion, population growth, and electrical circuits.
Polynomials can also be added, subtracted, and multiplied together to form new polynomials. Additionally, polynomials can be factored, which involves breaking them down into simpler polynomials that multiply together to give the original polynomial.
a) f(x)= 2x³ - 25x² + 53x - 30
⇒(x-1)(x-10)(2x-3)
b) f(x)= x³ + 3x - 4
⇒(x-1)(x² + x + 4)
To know more about factor visit:
https://brainly.com/question/26354419
#SPJ1
The complete question is:

Ryan invested \$4,800$4,800 in an account in the year 1990, and the value has been growing exponentially at a constant rate. The value of the account reached \$6,300$6,300 in the year 1998. Determine the value of the account, to the nearest dollar, in the year 2007.
Answers
well, from 1990 to 1998 is 8 years, and we know the amount went from $4800 to $6300, let's check for the rate of growth.
\(\qquad \textit{Amount for Exponential Growth} \\\\ A=P(1 + r)^t\qquad \begin{cases} A=\textit{accumulated amount}\dotfill & \$6300\\ P=\textit{initial amount}\dotfill &\$4800\\ r=rate\to r\%\to \frac{r}{100}\\ t=\textit{years}\dotfill &8\\ \end{cases} \\\\\\ 6300=4800(1 + \frac{r}{100})^{8} \implies \cfrac{6300}{4800}=(1 + \frac{r}{100})^8\implies \cfrac{21}{16}=(1 + \frac{r}{100})^8\)
\(\sqrt[8]{\cfrac{21}{16}}=1 + \cfrac{r}{100}\implies \sqrt[8]{\cfrac{21}{16}}=\cfrac{100+r}{100} \\\\\\ 100\sqrt[8]{\cfrac{21}{16}}=100+r\implies 100\sqrt[8]{\cfrac{21}{16}}-100=r\implies \stackrel{\%}{3.46}\approx r\)
now, with an initial amount of $4800, up to 2007, namely 17 years later, how much will that be with a 3.46% rate?
\(\qquad \textit{Amount for Exponential Growth} \\\\ A=P(1 + r)^t\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{initial amount}\dotfill &4800\\ r=rate\to 3.46\%\to \frac{3.46}{100}\dotfill &0.0346\\ t=years\dotfill &17\\ \end{cases} \\\\\\ A=4800(1 + 0.0346)^{17} \implies A=4800(1.0346)^{17}\implies A \approx 8558.02\)
Which of the following are possible solutions to this inequality?
SELECT ALL THAT APPLY :D
A) -2.75
B) -3
C) -2.5
D) -2.51

Answers
Answer:
I think the answer is a,b and d.
The population of a town is 75 000 and decreases 15% each year. Complete the exponential function that models the population afterx years
f(x) = 75,000
Answers
Answer:
Step-by-step explanation:
This is an exponential function of the form:
\(y=a(1-r)^x\) where a is the initial value and (1 - r) is the growth rate (which in our case is a decay, actually!). Our initial value is 75000 and our rate of change in the population is 15% or .15. Filling in our model:
\(y=75000(1-.15)^x\) and simplifying:
\(y=75000(.85)^x\) This turns out to be a decay problem because the value inside the parenthesis is less than 100%.
x is our time, so the model is as stated above.
REWRITE EACH PROBLEM AS A MULTIPLICATION QUESTION. MODEL YOUR ANSWER)12 gallons of water fill a tank to 3/4 capacity. 1: What is the capacity of the tank?2: If the tank is then filled to capacity, how many half gallon bottles can be filled with water in the tank.
Answers
1: if 3/4 is equal to 12 gallons then the capacity of the tank is 4(12)/3= 16 gallons
2: it can be filled 2x(16)=32 half gallon bottles
If mZOKL = 80°, then what is mZHKJ?
С
E
А4
N
H
K
M

Answers
so mHKJ is also 80°
cuanto da (9+4m)² cuadrado de binomio ayudaaaaa
Answers
Answer:
16m^2 + 72m + 81
Step-by-step explanation:
you expand it, by (9+4m)(9+4m), using distributive property you get
81 + 36m + 36m + 16m^2, simplifying you get the answer
Write the number marked with an arrow on the number line below as an improper (top-heavy) fraction

Answers
The number marked with an arrow on the number line below as an improper fraction is 2\(\frac{1}{2}\).
What is a number line?In elementary mathematics, a number line is a picture of a graduated straight line that serves as visual representation of the real numbers. Every point of a number line is assumed to correspond to a real number, and every real number to a point.In mathematics, an expression or mathematical expression is a finite combination of symbols that is well-formed according to rules that depend on the context.Mathematical symbols can designate numbers (constants), variables, operations, functions, brackets, punctuation, and grouping to help determine order of operations and other aspects of logical syntax.Given is a number line.
The number represented in the number line is -
2.5
or
5/2 = 2\(\frac{1}{2}\)
Therefore, the number marked with an arrow on the number line below as an improper fraction is 2\(\frac{1}{2}\).
To solve more questions on number line, visit the link below -
brainly.com/question/1041084
#SPJ1
Determine whether the series converges or diverges. (n+4)! a) 4!n!4" b) 1 \n(n+1)(n+2) =
Answers
We have to determine whether the given series converges or diverges. The given series is as follows: `(n+4)! / 4!(n!)` Let's use the ratio test to find out if this series converges or diverges.
The Ratio Test: It is one of the tests that can be used to determine whether a series is convergent or divergent. It compares each term in the series to the term before it. We can use the ratio test to determine the convergence or divergence of series that have positive terms only. Here, a series `Σan` is convergent if and only if the limit of the ratio test is less than one, and it is divergent if and only if the limit of the ratio test is greater than one or infinity. The ratio test is inconclusive if the limit is equal to one. The limit of the ratio test is `lim n→∞ |(an+1)/(an)|` Let's apply the Ratio test to the given series.
`lim n→∞ [(n+5)! / 4!(n+1)!] * [n!(n+1)] / (n+4)!` `lim n→∞ [(n+5)/4] * [1/(n+1)]` `lim n→∞ [(n^2 + 9n + 20) / 4(n^2 + 5n + 4)]` `lim n→∞ (n^2 + 9n + 20) / (4n^2 + 20n + 16)`
As we can see, the limit exists and is equal to 1/4. We can say that the given series converges. The series converges. To determine the convergence of the given series, we use the ratio test. The ratio test is a convergence test for infinite series. It works by computing the limit of the ratio of consecutive terms of a series. A series converges if the limit of this ratio is less than one, and it diverges if the limit is greater than one or does not exist. In the given series `(n+4)! / 4!(n!)`, the ratio test can be applied. Using the ratio test, we get: `
lim n→∞ |(an+1)/(an)| = lim n→∞ [(n+5)! / 4!(n+1)!] * [n!(n+1)] / (n+4)!` `= lim n→∞ [(n+5)/4] * [1/(n+1)]` `= lim n→∞ [(n^2 + 9n + 20) / 4(n^2 + 5n + 4)]` `= 1/4`
Since the limit of the ratio test is less than one, the given series converges.
The series converges to some finite value, which means that it has a sum that can be calculated. Therefore, the answer is a).
To learn more about ratio test visit:
brainly.com/question/31856271
#SPJ11
For the line segment whose endpoints are A(0, 0) and B(4, 3), find the x value for the point located 2/3 the distance from A to B
Answers
The x value for the point located 2/3 the distance from A to B is 2.67. This can be found by calculating the midpoint between A and B, which is (2, 1.5), and then taking 2/3 of the x component (2).
1. Calculate the midpoint between A and B: (0 + 4) / 2 = 2 and (0 + 3) / 2 = 1.5
2. Take 2/3 of the x component of the midpoint: 2/3 * 2 = 2.67
The value x for the point located 2/3 the distance from A to B can be found using a few simple steps. First, we need to calculate the midpoint between A and B. This can be done by adding the x and y components of the two points and then dividing by 2. For our points A and B, this gives us the midpoint (2, 1.5). Now, we need to take 2/3 of the x component of the midpoint (2). This gives us 2/3 * 2 = 2.67. This means that the x value for the point located 2/3 the distance from A to B is 2.67. This process can also be used to determine the y value for the point, which is 1.
Learn more about distance here
https://brainly.com/question/28956738
#SPJ4