The weights of newborn baby boys born at a local hospital are believed to have a normal distribution with a mean weight of 32843284 grams and a variance of 454,276454,276. If a newborn baby boy born at the local hospital is randomly selected, find the probability that the weight will be less than 43624362 grams. Round your answer to four decimal places.
Answers
The probability that a randomly selected newborn baby boy's weight at the local hospital is less than 43624362 grams is 1.0000 (or 100%).
To find the probability that a randomly selected newborn baby boy's weight at the local hospital is less than 43624362 grams, we can use the properties of the normal distribution.
Given that the distribution of newborn baby boys' weights is believed to be normal with a mean weight of 32843284 grams and a variance of 454276454276, we can calculate the standard deviation by taking the square root of the variance:
Standard deviation (σ) = √(454276454276) ≈ 674579.5906 grams
To find the probability, we need to standardize the value of 43624362 grams using the mean and standard deviation.
Z = (X - μ) / σ
where X is the value we want to standardize, μ is the mean, and σ is the standard deviation.
Standardizing the weight of 43624362 grams:
Z = (43624362 - 32843284) / 674579.5906
Z ≈ 17461.7622
Now, we can use the standard normal distribution table or a calculator to find the cumulative probability up to Z.
P(X < 43624362) = P(Z < 17461.7622)
Using the standard normal distribution table or a calculator, we find that the probability is extremely close to 1 (or 100%).
Rounded to four decimal places, the probability is 1.0000.
For similar question on probability.
https://brainly.com/question/30846562
#SPJ11
Related Questions
1 point
It took me 120 minutes to answer 25 questions. How long did each question take? type your answer...
Previous
minutes
Answers
It took me 120 minutes to answer 25 questions. How long did each question take?
120/25 = 4.8 minutes per question
Slope of a line is the measure of the
of a line.
Answers
Answer:
Slope, sometimes referred to as gradient in mathematics, is a number that measures the steepness and direction of a line, or a section of a line connecting two points, and is usually denoted by m. Generally, a line's steepness is measured by the absolute value of its slope, m.
Do I have to do Greatest Common denominator or do I factor it, or do I have to do AC grouping bc A doesn’t equal 1

Answers
The quadratic expression is
\(9y^2+12y-5\)Step 1: We will have to get two numbers that we will multiply to get (-45)
\(9\times-5=-45\)And the same two numbers must be added together to get
\(+12\)The numbers are ( -3 and +15)
\(\begin{gathered} -3\times15=-45 \\ -3+15=+12 \end{gathered}\)To get the two factors, we will need to list out all the factors of -45
Factors of -45 are
\(\begin{gathered} 1,3,5,9,15,45 \\ -1,-3,-5,-9,-15,-45 \end{gathered}\)Note: list the negative of each factor. This will allow us to find all possible combinations.
The factors below will multiply to give a product of -45
\(\begin{gathered} 1.(-45)=-45 \\ 3.(-15)=-45 \\ 5.(-9)=-45 \\ (-1).45=-45 \\ (-3).15=-45 \\ (-5).9=-45 \end{gathered}\)Now lets add up each pair and see which will give us +12
\(\begin{gathered} 1+(-45)=-44 \\ 3+(-15)=-12 \\ 5+(-9)=-4 \\ -1+45=+44 \\ -3+15=+12 \\ -5+9=+4 \end{gathered}\)From the table, we can see that the two numbers -3 and 15 add to 12 (the middle coefficient).
So the two numbers -3 and 15 both multiply to -45 and add to 12
Now replace the middle term 12x with -3y + 15y. Remember, -3 and 15 add to 12. So this shows us that -3y + 15y=12y
\(\begin{gathered} 9y^2+12y-5 \\ =9y^2-3y+15y-5 \end{gathered}\)Group the terms into two pairs
\(\begin{gathered} (9y^2-3y)+(15y-5) \\ \end{gathered}\)Factor out the G.C.F 3y from the first group and the G.C.F 5 from the second group
\(\begin{gathered} (9y^2-3y)+(15y-5) \\ 3y(3y-1)+5(3y-1) \end{gathered}\)The goal of this step is to make the terms in the second parenthesis equal to the terms in the first parenthesis.
Combine like terms. Or factor out the common term (3x-1)
\(\begin{gathered} 3y(3y-1)+5(3y-1) \\ (3y-1)(3y+5) \end{gathered}\)Hence,
9y² +12y -5 = (3y-1) (3y+5)

Find the curvature of r(t) =< t^2,ln t,t ln t > at the point
Answers
To find the curvature of the curve defined by the vector function r(t) = < t^2, ln(t), t ln(t) > at a given point, we need to calculate the curvature using the formula:
κ = |dT/ds| / ||dT/ds||,
where dT/ds is the unit tangent vector and ||dT/ds|| is its magnitude.
Let's proceed with the calculations:
Step 1: Find the first derivative of r(t) to get the tangent vector T(t):
r'(t) = < 2t, 1/t, ln(t) + t/t > = < 2t, 1/t, ln(t) + 1 >.
Step 2: Calculate the magnitude of the tangent vector:
||r'(t)|| = sqrt((2t)^2 + (1/t)^2 + (ln(t) + 1)^2)
= sqrt(4t^2 + 1/t^2 + ln(t)^2 + 2ln(t) + 1).
Step 3: Differentiate r'(t) to find the second derivative:
r''(t) = < 2, -1/t^2, 1/t + 2/t > = < 2, -1/t^2, (t + 2)/t >.
Step 4: Calculate the magnitude of the second derivative:
||r''(t)|| = sqrt(2^2 + (-1/t^2)^2 + ((t + 2)/t)^2)
= sqrt(4 + 1/t^4 + (t^2 + 4t + 4)/t^2)
= sqrt((t^6 + 4t^5 + 4t^4) + (t^2 + 4t + 4) + 4t^2).
Step 5: Calculate the curvature:
κ = |dT/ds| / ||dT/ds||
= (||r'(t)|| / ||r''(t)||^3)
= ((sqrt(4t^2 + 1/t^2 + ln(t)^2 + 2ln(t) + 1)) / (sqrt((t^6 + 4t^5 + 4t^4) + (t^2 + 4t + 4) + 4t^2))^3).
To find the curvature at a specific point, substitute the value of t into the expression for κ.
To know more about curvature refer here
https://brainly.com/question/30106465#
#SPJ11
7/8 - 1/4=
Explain how you got your answer
Answers
Answer:5/8
Step-by-step explanation: transform the expression 8 so 7-2/8 =5/8
Answer:
5/8.
Step-by-step explanation:

Help asap please!
in a class project, breanne determines that her plant growth can be described by the equation y = 0.25x + 2 where x = days and y = height of the plant in centimeters,
in the equation, what does 0.25 represent?
a the growth of the planet each day
b the total height of the plant after x days
c the height of the plant on the first day breanne bagan recording its
growth
d the total number of days that breanne has been recording the plant
growth
Answers
In the given equation y = 0.25x + 2, 0.25 represents (A) the daily growth of the plant.
What are equations?An equation is a mathematical statement that contains the symbol "equal to" between two expressions with identical values. as in 3x + 5 = 15, for example.
There are many different types of equations, including linear, quadratic, cubic, and others.
The three primary forms of linear equations are point-slope, standard, and slope-intercept.
So, the given equation is:
y = 0.25x + 2
Where x is the days and y is the height.
Now, if we observe the equation, 2 is the height of the plant on day one from where the recording started.
we already know that x is the day and y is the height.
Then, 0.25 will be the growth of the plant each day.
Therefore, in the given equation y = 0.25x + 2, 0.25 represents (A) the daily growth of the plant.
Know more about equations here:
https://brainly.com/question/28937794
#SPJ4
HELP PLS HELP PLS!!!!IWILLLLLLL MARK BRAINLIEST

Answers
Check the picture below.
50 minutes later, well, each cat has been running for 50 minutes, so same time for each. Let's say the rate of A is slower so is "r" and the rate of B is twice that much or "2r". Now, by the time 50 minutes passed, they're 750 meters apart, that means if cat A has covered "d" meters then cat B has covered that much plus 750 meters, as you see in the picture.
\({\Large \begin{array}{llll} \underset{distance}{d}=\underset{rate}{r} \stackrel{time}{t} \end{array}} \\\\[-0.35em] ~\dotfill\\\\ \begin{array}{lcccl} &\stackrel{meters}{distance}&\stackrel{m/min}{rate}&\stackrel{minutes}{time}\\ \cline{2-4}&\\ A&d&r&50\\ B&d+750&2r&50 \end{array}\hspace{5em} \begin{cases} d=(r)(50)\\\\ d+750=(2r)(50) \end{cases} \\\\[-0.35em] ~\dotfill\)
\(\stackrel{\textit{we know that}}{d=50r}\hspace{5em}\stackrel{\textit{substituting on the 2nd equation}}{(50r)~~ + ~~750=(2r)(50)} \\\\\\ 50r+750=100r\implies 750=50r\implies \cfrac{750}{50}=r\implies \stackrel{ \textit{\LARGE A} }{\boxed{15=r}}~\hfill~\stackrel{ \textit{\LARGE B} }{\boxed{2r=30}}\)

Divide. 5x + 3/5x3 - 22x2 - 40x – 15
The answer is N
(Simplify your answer.)
Answers
Answer:
\(n=\frac{386x-75}{5}\)
Step-by-step explanation:
Add like terms
\(-35x+3\cdot \frac{3}{5}x-22\cdot \:2x-15=n\)
Add 15 on both sides
\(-35x+\frac{9}{5}x-44x-15+15=n+15\)
Simplify
\(-35x+\frac{9}{5}x-44x=n+15\)
Multiply sides by 5
\(-35x\cdot \:5+\frac{9}{5}x\cdot \:5-44x\cdot \:5=n\cdot \:5+15\cdot \:5\)
Simplify
\(-386x=5n+75\)
Divide both sides
\(\frac{-386x}{-386}=\frac{5n}{-386}+\frac{75}{-386}\)
You will get
\(x=-\frac{5n+75}{386}\)
Then you will solve for n using x
Multiply both sides by 386
\(\frac{386\left(5n+75\right)}{386}=386x\)
Simplify
\(5n+75=386x\)
Subtraction
\(5n+75-75=386x-75\)
Simplify
\(5n=386x-75\)
Divide by 5 to get n
\(\frac{5n}{5}=\frac{386x}{5}-\frac{75}{5}\)
\(n=\frac{386x-75}{5}\)
If Garou has 5 apples, and gives 2 to saitama and 3 to Master Bang, how many apples dose Garou have?
Answers
Answer: Garou has 0 apples left.
Step-by-step explanation: 5-2-3 = 0
Answer:
He will have no Apples left.
Step-by-step explanation:
5 - 2 = 3. So when Garou gave Saitama 2 apples, he now has 3 left because he also had 5 apples. Finally Garou gave 3 apples to Master Bang which leaves him with no apples cuz remember he had 5, and then gave 2 to Saitama now he has 3. And he gave 3 to Master Bang and now he has no apples. The answer is 0. Garou has no apples left.
Please help 3/4
Solve the binomial
(2ab-3c)(2ab+3c)
Answers
Answer:
I’m answering so the other peep can get brainliest she’s correct I think I’m pretty sure I think so thx for points have a great day byee
Step-by-step explanation:
The box plot represents the distribution of the number of points scored by a cross country team at 12 meets.
22 24 26 28 30 32 34 36 38 40 42
points
If possible, find the mean. If not possible, explain why not.
Answers
Answer:It is not possible
Step-by-step explanation: It is not possible because we need 12 plot to solve for an accurate mean but there is only 11 data which is impossible.
If f(x) = 5x−4, find f(2)
A. 10
B. 48
C. 2
D. 6
Answers
Answer:
D. 6
Step-by-step explanation:
f(x) = 5x - 4
f(2) = 5(2) - 4 The 2 is substituted into the equation where 'x' is.
f(2) = 10 - 4
f(2) = 6
A sample of 64 observations is selected from a normal population. The sample mean is 215 , and the population standard deviation is 15 Conduct the following test of hypothesis using the 0.025 significance level. H 0
μ≥220 H 1
:μ<220 a. Is this a one-or two-tailed test? One-talled test Two-talled test b. What is the decision rule? (Negative amount should be indicated by a minus sign. Round your answer to 2 decimal places.) c. What is the value of the test statistic? (Negative amount should be indicated by a minus sign. Round your answer to 2 decimal places.) c. What is the value of the test statistic? (Negative amount should be indicated by a minus sign. Round your answer to 2 decimal places.) d. What is your decision regarding H 9
? Reject Do not reject e. What is the p-value? (Round your answer to 4 decimal places.)
Answers
a. This is a one-tailed test because the alternative hypothesis, \(H_1\), states that the population mean is less than 220, indicating a specific direction.
b. Reject \(H_0\) if the test statistic (Z-score) is less than -1.96.
c. The value of the test statistic (Z-score) is -2.67.
d. the decision regarding H0 is to reject it.
e. The p-value is 0.0038.
a. The alternative hypothesis, \(H_1\), asserts that the population mean is smaller than 220, indicating a particular direction, hence this is a one-tailed test.
b. If the test statistic is less than the crucial value, the null hypothesis, \(H_0\), is to be rejected in a one-tailed test at the 0.025 significance level. The critical value can be determined based on the significance level and the sample size. Since the significance level is 0.025 and the test is one-tailed, we can find the critical value from a standard normal distribution table or calculator.
Looking up the critical value for a significance level of 0.025, we find it to be approximately -1.96. Therefore, the decision rule is:
Reject \(H_0\) if the test statistic (Z-score) is less than -1.96.
c. The test statistic (Z-score) can be calculated using the formula:
Z = (sample mean - population mean) / (population standard deviation / √(sample size))
Plugging in the values:
Z = (215 - 220) / (15 / √(64))
Z = -5 / (15 / 8)
Z = -5 * (8/15)
Z = -2.67 (rounded to 2 decimal places)
Therefore, the test statistic's (Z-score) value is -2.67.
d. Based on the decision rule, we compare the test statistic to the critical value. Since the test statistic (-2.67) is less than the critical value (-1.96), we reject the null hypothesis, \(H_0\).
Therefore, \(H_0\) is to be rejected as a result of the ruling.
e. The p-value represents the probability of obtaining a test statistic as extreme as or more extreme than the observed value, assuming the null hypothesis is true. In this case, since the test is one-tailed and we reject \(H_0\), the p-value is the probability of observing a test statistic less extreme than -2.67.
Looking up the p-value for a Z-score of -2.67 in a standard normal distribution table or calculator, we find the p-value to be approximately 0.0038 (rounded to 4 decimal places).
Therefore, the p-value is 0.0038.
Learn more about null hypothesis on:
https://brainly.com/question/28042334
#SPJ4
Solve for x.
X
A
=
2
C
1
B
1
E
X
D
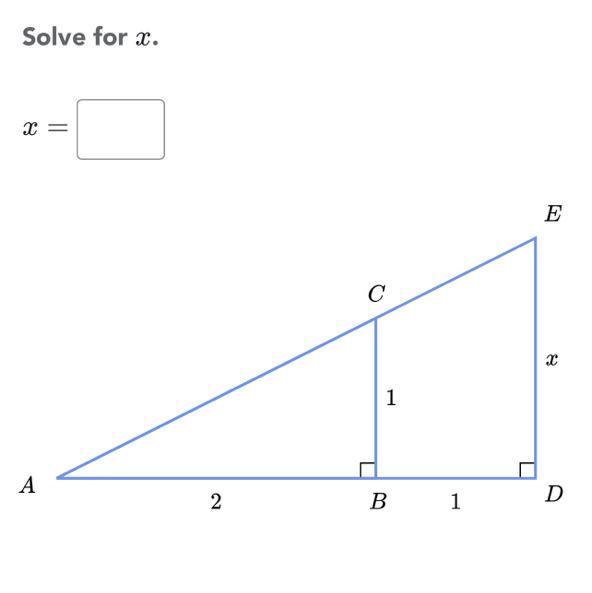
Answers
Step-by-step explanation:
ABC and ADE are similar triangles.
that means they have the same angles, and there is one scaling factor for all sides from one triangle to the other.
so, we see that AB = 2, AD = 2+1 = 3
the scaling factor f from AB to AD is then
AB × f = AD
2 × f = 3
f = 3/2
the same scaling factor now applies between BC and DE (= x).
BC × f = x
1 × 3/2 = x
x = 3/2 = 1.5
True or false? the interval [1,2] contains exactly two numbers - the numbers 1 and 2.
Answers
The answer is "false". The interval [1, 2] contains all the real numbers between 1 and 2 including the endpoints.
How to write and represent an interval?An interval notation is used for representing the continuous set of real values. This is the shortest way of writing inequalities.
Intervals are represented within the brackets such as square brackets or open brackets(parenthesis).
If the interval is within a square bracket, then the end values are included in the set of values.If the interval is within parenthesis, then the end values are not included in the set of values.The square brackets represent the inequalities - 'greater than or equal or 'less than or equalThe parenthesis represents the inequalities - 'greater than' or 'less thanFinding true or false:The given interval is [1, 2]
The given statement is - 'the interval [1, 2] contains exactly two numbers - the numbers 1 and 2'
The given statement is 'false'.
This is beacuse, an interval consists set of all the real values in between the two values given.
So, according to the definition, there are not only the end values but also many real values in between them.
Thus, the answer is "false". The interval [1, 2] consists of all the real values between 1 and 2 including 1 and 2.
Learn more about interval notation here:
https://brainly.com/question/10878781
#SPJ4
What percent of the votes are for cake? Round to the nearest percent.
Ice Cream -12
Brownie-7
Cookie-3
Cake-10
Answers
31% of the votes are for cake.
The percentage is the ratio of an item expressed as a fraction out of 100.
Given :
Number of votes for ice cream = 12
Number of votes for brownie = 7
Number of votes for Cookie = 3
Number of votes for cake = 10
Total number of votes = 12 + 7 + 3 + 10 = 32
Percentage of items = Number of Items * 100
Total Number of Items
Percentage of votes for cake
= Number of votes for cake * 100
Total number of votes
= 10 * 100
32
= 31.25 %
~ 31 %
Similar problems related to percentage,
https://brainly.com/question/29123711
Find the value of cos Q rounded to the nearest bundredth, if necessary,

Answers
Answer:
0.44
Step-by-step explanation:
Cosine is equal to the adjacent side divided by the hypotenuse.
For Q' this would be 11/25. 11/25=0.44
How do you find the missing side of a triangle?
Answers
The missing sides of the triangle can be found by applying the Pythagoras Theorem .
What is Pythagoras Theorem ?
The Pythagoras Theorem states that square of hypotnuse (that is longest side) is equal to sum of the square of perpendicular and base .
that means : \(Hypotnuse^{2} = Perpendicular^{2} +Base^{2}\) ;
let missing side of the Right triangle be hypotnuse ;
So , missing side is written as : \(Hypotnuse = \sqrt{Perpendicular^{2} +Base^{2}}\) .
For Example : Let a right triangle has sides lengths of perpendicular = 6 and hypotnuse = 10 .
let , the length of side "base" be unknown.
So , in order to find length of side b (base) , we substitute the known values into Pythagoras theorem:
\(10^{2} =6^{2} +Base^{2}\) ;
\(Base = 100-36\) ;
So , missing side "base" is = 8 ;
Therefore , the missing side can be found by using the Pythagoras Theorem .
Learn more about Triangles here
https://brainly.com/question/30104289
#SPJ4
You are in charge of getting food for the class from the corner store. You can buy
chips for $2 or a hoagie for $5. There are 19 students in the class, so you need to buy
at least 19 items, and you have $77 total.
Write a system of equations to represent this situation. Use x to represent the number
of chips and y to represent the number of hoagies.
Separate each inequality with a comma,
Answers
The system of inequalities to represent the situation is 2x + 5y ≤ 77, x + y ≥ 19
How to represent a situation with inequality?You are in charge of getting food for the class from the corner store. You can buy chips for $2 or a hoagie for $5.
There are 19 students in the class, so you need to buy at least 19 items, and you have $77 total.
Hence, the system of inequality to represent this situation is as follows:
let
x = number of chips
y = number of hoagies
Therefore, the inequalities is as follows:
2x + 5y ≤ 77
x + y ≥ 19
learn more on inequality here:https://brainly.com/question/2155328
#SPJ1
Joanna bakes a cake in the shape of a
cylinder. The cake is 10 inches in
diameter and 4.5 inches tall. She
wants to put frosting on the entire
cake that is not resting on the tray.
How many square inches of frosting
will she need? im confused on how to do the work. please answer quickly
Answers
Answer:
total surface area = 298.45105 m2
lateral surface area = 141.37155 m2
top surface area = 78.53975 m2
bottom surface area = 78.53975 m2
Step-by-step explanation:
Joanna will need approximately 298.3 square inches of frosting to cover the entire cake.
To calculate the amount of frosting Joanna will need for the entire cake, we first need to find the surface area of the cylindrical cake.
The formula for the surface area of a cylinder is given by:
Surface Area = 2πr² + 2πrh
Where r is the radius of the base and h is the height of the cylinder.
Given that the diameter of the cake is 10 inches, we can find the radius by dividing it by 2: r = 10/2 = 5 inches.
Plugging in the values, we have:
Surface Area = 2π(5)² + 2π(5)(4.5)
Simplifying the equation:
Surface Area = 2π(25) + 2π(22.5)
Surface Area = 50π + 45π
Surface Area = 95π
To find the actual numerical value, we can approximate π as 3.14:
Surface Area ≈ 95 * 3.14
Surface Area ≈ 298.3 square inches
To learn more about cylinder click on,
https://brainly.com/question/24309865
#SPJ2
WHO IS THE BEST QUINTUPLET
1. Ichika
2.Miku
3.Nino
4.Yotsuba
5.Itsuki
WERE SETTLING THIS ONCE AND FOR ALLLLL!
Answers
Answer:
the beef is settled, its itsuki or miku
Step-by-step explanation:
!!PLEASE HELP!!
Will mark brainliest
Look at the picture^^

Answers
Answer:
u=UMMM this is your teacher you should not be asking for your answers online you got a zero
Step-by-step explanation:
Nadia is mountain climbing. She started at an altitude of 19.26 feet below sea level and then changed her altitude by climbing a total of 5,437.8 feet up from her initial position. What was Nadia's altitude at the end of her climb?
Answers
Answer:
5,418.2 feet
Step-by-step explanation:
Nadia is carrying out mountain climbing.
She started climbing the mountain at an altitude of 19.26 feet below the sea level.
Nadia changed her altitude by climbing a total of 5,437.8 feet from her starting position.
Therefore, Nadia's altitude at the end of her climb can be calculated as follows
= 5,437.8-19.6
= 5,418.2
Hence Maria's altitude at the end of her climb is 5,418.2 feet
Answer:
5,418.2 feet
Step-by-step explanation:
0.3log(x+1)+0.3sin x+2
State the Local Max and Local Min. Justify your answer with
reference to the graph of this function and the sign of IRC.
Provide a sketch of your function.
Answers
The function f(x) = 0.3log(x+1) + 0.3sin(x) + 2 has a local maximum and a local minimum.
To determine the local maxima and minima, we need to find the critical points of the function by setting its derivative equal to zero and solving for x.
Taking the derivative of f(x) with respect to x, we get:
f'(x) = 0.3/(x+1) + 0.3cos(x)
To find the critical points, we set f'(x) = 0:
0.3/(x+1) + 0.3cos(x) = 0
Multiplying through by (x+1), we have:
0.3 + 0.3(x+1)cos(x) = 0
0.3 + 0.3xcos(x) + 0.3cos(x) = 0
0.3xcos(x) + 0.3cos(x) = -0.3
Dividing through by 0.3, we obtain:
xcos(x) + cos(x) = -1
Factoring out cos(x), we get:
cos(x)(x+1) = -1
Since the cosine function oscillates between -1 and 1, there are two possibilities for the critical points:
1. cos(x) = -1 and x + 1 ≠ 0
2. cos(x) = 1 and x + 1 ≠ 0
For cos(x) = -1, x must be an odd multiple of π. However, we exclude x = -1 from the critical point because x + 1 must not equal zero. Therefore, there is no critical point in this case.
For cos(x) = 1, x must be an even multiple of π. Again, excluding x = -1, we find that x = -2π, -4π, -6π, etc., are the critical points.
Now, we can examine the sign of the first derivative in the intervals around these critical points to determine the local maxima and minima.
In the interval (-∞, -2π), f'(x) < 0, indicating a decreasing slope.
In the interval (-2π, -4π), f'(x) > 0, indicating an increasing slope.
In the interval (-4π, -6π), f'(x) < 0, indicating a decreasing slope.
From this information, we can deduce that there is a local maximum at x = -2π and a local minimum at x = -4π.
To sketch the function, we consider the behavior of the function as x approaches positive and negative infinity. As x approaches negative infinity, both the logarithmic and sine terms become negligible compared to the constant term 2. Therefore, the graph approaches a horizontal line at y = 2. As x approaches positive infinity, the logarithmic term dominates, and the graph approaches a vertical asymptote at x = -1.
Based on this information, we can sketch the graph of the function with a local maximum at x = -2π and a local minimum at x = -4π, approaching a horizontal line at y = 2 and having a vertical asymptote at x = -1.
Please note that without specific values for the range and precise characteristics of the function, the sketch is a general representation of its behavior.
Learn more about function here
https://brainly.com/question/11624077
#SPJ11
use induction to prove that = n^2 (2n^2 − 1) whenever n is a positive integer.
Answers
To prove the equation P(n) = n^2 (2n^2 - 1) for all positive integers n using induction, we need to show two things:
1. Base Case: P(1) is true.
2. Inductive Step: Assuming P(k) is true for some positive integer k, we need to show that P(k+1) is also true.
Base Case:
Let's substitute n = 1 into the equation P(n) = n^2 (2n^2 - 1):
P(1) = 1^2 (2(1)^2 - 1) = 1(2 - 1) = 1(1) = 1.
Therefore, P(1) is true.
Inductive Step:
Assume that P(k) is true for some positive integer k, which means:
P(k) = k^2 (2k^2 - 1).
We need to show that P(k+1) is true:
P(k+1) = (k+1)^2 (2(k+1)^2 - 1)
= (k+1)^2 (2(k^2 + 2k + 1) - 1)
= (k+1)^2 (2k^2 + 4k + 2 - 1)
= (k+1)^2 (2k^2 + 4k + 1).
Expanding further:
P(k+1) = 2k^2(k+1)^2 + 4k(k+1)^2 + (k+1)^2
= 2k^2(k^2 + 2k + 1) + 4k(k^2 + 2k + 1) + (k^2 + 2k + 1)
= 2k^4 + 4k^3 + 2k^2 + 4k^3 + 8k^2 + 4k + k^2 + 2k + 1
= 2k^4 + 8k^3 + 11k^2 + 6k + 1.
Notice that this expression is the sum of P(k) = k^2 (2k^2 - 1) and additional terms:
P(k+1) = k^2 (2k^2 - 1) + 2k^4 + 6k^3 + 8k^2 + 6k + 1.
Simplifying this expression:
P(k+1) = 2k^4 + 6k^3 + 8k^2 + 6k + 1
= (k^2 (2k^2 - 1)) + (2k^4 + 6k^3 + 8k^2 + 6k + 1)
= P(k) + (2k^4 + 6k^3 + 8k^2 + 6k + 1).
Since we assumed P(k) is true, we can substitute it:
P(k+1) = P(k) + (2k^4 + 6k^3 + 8k^2 + 6k + 1)
= k^2 (2k^2 - 1) + (2k^4 + 6k^3 + 8k^2 + 6k + 1)
= 2k^4 + 4k^4 - k^2 + 6k^3 + 8k^2 + 6k + 1
= 6k
To learn more about positive integers: -brainly.com/question/18380011
#SPJ11
To prove the equation P(n) = n^2 (2n^2 - 1) for all positive integers n using induction, we need to show two things:
1. Base Case: P(1) is true.
2. Inductive Step: Assuming P(k) is true for some positive integer k, we need to show that P(k+1) is also true.
Base Case:
Let's substitute n = 1 into the equation P(n) = n^2 (2n^2 - 1):
P(1) = 1^2 (2(1)^2 - 1) = 1(2 - 1) = 1(1) = 1.
Therefore, P(1) is true.
Inductive Step:
Assume that P(k) is true for some positive integer k, which means:
P(k) = k^2 (2k^2 - 1).
We need to show that P(k+1) is true:
P(k+1) = (k+1)^2 (2(k+1)^2 - 1)
= (k+1)^2 (2(k^2 + 2k + 1) - 1)
= (k+1)^2 (2k^2 + 4k + 2 - 1)
= (k+1)^2 (2k^2 + 4k + 1).
Expanding further:
P(k+1) = 2k^2(k+1)^2 + 4k(k+1)^2 + (k+1)^2
= 2k^2(k^2 + 2k + 1) + 4k(k^2 + 2k + 1) + (k^2 + 2k + 1)
= 2k^4 + 4k^3 + 2k^2 + 4k^3 + 8k^2 + 4k + k^2 + 2k + 1
= 2k^4 + 8k^3 + 11k^2 + 6k + 1.
Notice that this expression is the sum of P(k) = k^2 (2k^2 - 1) and additional terms:
P(k+1) = k^2 (2k^2 - 1) + 2k^4 + 6k^3 + 8k^2 + 6k + 1.
Simplifying this expression:
P(k+1) = 2k^4 + 6k^3 + 8k^2 + 6k + 1
= (k^2 (2k^2 - 1)) + (2k^4 + 6k^3 + 8k^2 + 6k + 1)
= P(k) + (2k^4 + 6k^3 + 8k^2 + 6k + 1).
Since we assumed P(k) is true, we can substitute it:
P(k+1) = P(k) + (2k^4 + 6k^3 + 8k^2 + 6k + 1)
= k^2 (2k^2 - 1) + (2k^4 + 6k^3 + 8k^2 + 6k + 1)
= 2k^4 + 4k^4 - k^2 + 6k^3 + 8k^2 + 6k + 1
= 6k
To learn more about integers: -brainly.com/question/490943
#SPJ11
if [0 0 0 1 0] is one row in an echelon form of an augmented matrix, then the associated linear system is always consistent. true or false?
Answers
The statement is true. If the row [0 0 0 1 0] is in echelon form of an augmented matrix, then the associated linear system is always consistent. This means there is at least one solution to the system of linear equations.
Echelon form is a type of row-echelon form that has specific properties. In echelon form, the leading coefficient (non-zero element) of each row is strictly to the right of the leading coefficient of the row above it. In the given row [0 0 0 1 0], the leading coefficient is 1, and it is the only non-zero element in the row.
In an augmented matrix, the rightmost column represents the constants or the right-hand side of the linear equations. Since the leading coefficient in the given row is 1 and there are no non-zero elements to the left of it, this implies that the associated linear equation is of the form 0x + 0y + 0z + w = 0. This equation simplifies to w = 0.
Since w is a free variable and its value can be chosen as 0, the linear system is consistent. Every consistent system has at least one solution, and in this case, the solution is when w = 0, while x, y, and z can take any values.
Therefore, if [0 0 0 1 0] is one row in an echelon form of an augmented matrix, the associated linear system is always consistent.
Learn more about echelon form here: brainly.com/question/28767094
#SPJ11
A store purchased 250 pastries for $100. They resold all 250 pastries for $150. What is the store’s profit per pastry?
Answers
Answer:
the profit is $1.66 per pastry
Step-by-step explanation:
Answer:
The profit is 20 cents per pastry
Step-by-step explanation:
What is the y-intercept of

Answers
Answer:
(0, 1)
Step-by-step explanation:
Answer:
(B). (0, 1)
Step-by-step explanation:
Coordinates of y-intercept are (0, y)
\(a^{0} = 1\)
y = f(x) = \((\frac{3}{5}) ^{0}\) = 1
(0, 1)
SNOWFALL In February 2015, South Bend, Indiana , saw one of its snowiest Februarys on record. The snowfall in February 2015 was 0.6 inch more than twice the snowfall in February 2020. The snowfall in February 2015 was also 8.35 inches fewer than 2.5 times the snowfall in February 2020. Write and solve an equation to find the amount of snowfall in February 2015 and in February 2020 .
Answers
The amount of snowfall in February 2015 was 36.4 inches and the amount of snowfall in February 2020 was 17.9 inches
Solving system of equationsFrom the question, we are to determine the amount of snowfall in February 2015 and in February 2020
Let the amount of snowfall in February 2015 be x
and the amount of snowfall in February 2020 by y
From the given information,
"The snowfall in February 2015 was 0.6 inch more than twice the snowfall in February 2020"
That is,
x = 0.6 + 2y
Also, from the information
"The snowfall in February 2015 was also 8.35 inches fewer than 2.5 times the snowfall in February 2020"
x = 2.5y - 8.35
Now,
Solve the system of equations simultaneously
x = 0.6 + 2y -------- (1)
x = 2.5y - 8.35 -------- (2)
Equate equations (1) and (2)
0.6 + 2y = 2.5y - 8.35
0.6 + 8.35 = 2.5y - 2y
8.95 = 0.5y
y = 8.95/0.5
y = 17.9
Substitute the value of y into equation (1)
x = 0.6 + 2y
x = 0.6 + 2(17.9)
x = 0.6 + 35.8
x = 36.4
Hence, the amount of snowfall in February 2015 was 36.4 inches and the amount of snowfall in February 2020 was 17.9 inches
Learn more on Solving system of equations here: https://brainly.com/question/13729904
#SPJ1
Anthony wants to start making periodic investments in a retirement account. He will make a yearly contribution of $3,000 at the beginning of each year. The account will pay 7.2% interest, compounded monthly. How much will his account be worth after 35 years?
Answers
The amount of money remaining in Anthony account after 35 years would be $37006.08
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
Given that the amount invested (P) = $3000, the period (t) = 35 years, number of times compounded yearly = 12 (monthly), rate (r) = 7.2% = 0.072
Hence, the final amount (A) is:
\(A=P(1+\frac{r}{n} )^{nt}\\\\A=3000(1 + \frac{0.072}{12})^{35*12}\\ \\A=$37006.09\)
The amount of money remaining in Anthony account after 35 years would be $37006.08
Find out more on equation at: https://brainly.com/question/13763238
#SPJ1