Theoretical Probability and Random Processes.
If you could please provide a detailed answer I will be sure to
upvote.
Thank you in advanced.
20. (a) If U and V are jointly continuous, show that P(U = V) = 0. (b) Let X be uniformly distributed on (0, 1), and let Y = X. Then X and Y are continuous, and P(X = Y) = 1. Is there a contradiction
Answers
A. P(U = V) = ∫∫f(u,v)dudv = ∫∫f(u,u)dudv = ∫(∫f(u,u)du)dv = 0
B. There is no contradiction.
Theoretical Probability and Random Processes:
Theoretical probability is an outcome of an experiment based on the number of expected positive outcomes divided by the total number of possible outcomes.
Random processes refer to a sequence of random variables. These variables are indexed to some parameter, most commonly time.
Below, the answers to part a) and b) have been provided along with the explanation:
(a) If U and V are jointly continuous, then show that P(U = V) = 0.
Here, we know that U and V are jointly continuous, and P(U = V) = 0. We are required to prove this statement, which can be done as follows: Since U and V are jointly continuous random variables, their joint probability density function is given by:
f(u,v) = Fuv(u,v), for u and v in some domain.
Now, we have:
P(U = V) = ∫∫f(u,v)dudv, where the integral ranges over the diagonal line in the domain {(u, v) : u = v}.
For all u, v in the domain, U = V is a straight line, and therefore, we can set v = u in the joint pdf to get:
f(u,u) = Fuv(u,u).
Thus, we have:
P(U = V) = ∫∫f(u,v)dudv = ∫∫f(u,u)dudv = ∫(∫f(u,u)du)dv = 0
(b) Let X be uniformly distributed on (0,1), and let Y = X. Then X and Y are continuous, and P(X = Y) = 1. Is there a contradiction?
Here, we have X and Y as uniform random variables defined on (0, 1). The probability density function of X is:
fX(x) = 1, 0 ≤ x ≤ 1
and that of Y is:
fY(y) = 1, 0 ≤ y ≤ 1
The probability of X = Y is:
P(X = Y) = P(X ∈ (0, 1), Y ∈ (0, 1), X = Y)
Thus, we have:
P(X = Y) = P(X ∈ (0, 1), Y ∈ (0, 1)) = ∫10 ∫10 fX(x)fY(y)dxdy = ∫10 ∫10 dxdy = 1.
There is no contradiction as the random variables X and Y are both continuous, and P(X = Y) = 1.
To learn more about contradiction, refer below:
https://brainly.com/question/28568952
#SPJ11
(a) yes, the probability of two continuous random variables being equal is mathematically determined to be zero.
Jointly continuous probability distributions involve two or more continuous random variables with a joint probability density function that is positive across the entire range of the variables. In such distributions, the probability of two variables having the exact same value is considered to be zero. This is because the probability assigned to each combination of values is positive, indicating that the probability is spread out over a continuous range rather than concentrated at specific points.
Consequently, the probability of two continuous random variables being equal is mathematically determined to be zero.
(b) Yes there is a contradiction between part (a) and part (b) due to the nature of jointly continuous distributions and the assumption made in the uniform distribution example.
Let's consider the case of two continuous random variables, X and Y, uniformly distributed over the interval (0,1). The probability density function (pdf) for a continuous uniform distribution in this interval is given by:
f(x) = 1/(b-a) for a ≤ x ≤ b
In our scenario, a = 0 and b = 1, resulting in the pdf:
f(x) = 1 for 0 ≤ x ≤ 1
Now, we aim to calculate the probability, P(X=Y). This can be expressed as:
P(X=Y) = P(X-Y = 0)
If X - Y = 0, it implies that X = Y. However, as mentioned in part (a), the probability of two continuous random variables being equal is mathematically determined to be zero. Therefore, P(X = Y) cannot be equal to 1. This contradiction arises when comparing the characteristics of jointly continuous distributions (where the probability of two variables being equal is zero) and the uniform distribution (where the probability of two variables being equal is mistakenly assumed to be one).
In conclusion, there is a contradiction between part (a) and part (b) due to the nature of jointly continuous distributions and the assumption made in the uniform distribution example.
To know more about continuous probability distributions, refer here:
https://brainly.com/question/31503218#
https://brainly.com/question/31114893#
#SPJ11
Related Questions
Write an equation that can be used to describe the relationship between x and y shown in the graph in the image

Answers
Answer:
\(y=-2x+3\)
Step-by-step explanation:
Equation of straight line in slope intercept form is given as
\(y=mx+b\)
Here
Slope of line m=-2 (for every one step on x-axis line going down 2 step on y-axis)
y-intercept b=3
\(y=-2x+3\)
let s = {1, 2, 3, 4} and let f denote the set of all nonempty subsets of s that have at most two elements. draw the intersection graph of f.
Answers
The subsets of s with one or two elements are:
{1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4} and the intersection graph is drawn below.
To draw the intersection graph of the nonempty subsets of set s = {1, 2, 3, 4} that have at most two elements, we need to consider all possible subsets of s with one or two elements and draw edges between subsets that have a non-empty intersection.
The subsets of s with one or two elements are:
{1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}
Now, let's draw the intersection graph:
Start by representing each subset as a vertex.
Draw edges between vertices if the corresponding subsets have a non-empty intersection.
The intersection graph of the nonempty subsets of s with at most two elements is as follows:
{1} --- {1, 2}
| / \
{2} / {1, 3}
| / /
{3} --- {1, 4}
|
{4} --- {2, 3}
|
{3, 4} --- {2, 4}
More can be learned about subsets
brainly.com/question/17514113
#SPJ4
what is the inequality 3 < p/9 solved? and what the graph look like?
Answers
The graph indicates that any value of p to the right of the open circle (greater than 27) satisfies the inequality 3 < p/9.
To solve the inequality 3 < p/9, we can start by multiplying both sides of the inequality by 9 to eliminate the fraction:
3 * 9 < p
27 < p
So the solution to the inequality is p > 27.
Now, let's graph the solution on a number line. Since the inequality is p > 27, we will represent it with an open circle at 27 and an arrow pointing to the right to indicate that the values of p are greater than 27. Here's how the graph would look:
markdown
Copy code
----------------------> (number line)
o
27
The graph indicates that any value of p to the right of the open circle (greater than 27) satisfies the inequality 3 < p/9.
For such more questions on Inequality Solution
https://brainly.com/question/30604125
#SPJ8

HELPPPPP!!!!! Is the following number rational or irrational? \sqrt{99} Choose 1 answer: Choose 1 answer: (Choice A) A Rational (Choice B) B Irrational
Answers
Answer:
√99 is irrational
Step-by-step explanation:
Answer:Irrational
Step-by-step explanation:
bc khan
What is an equivalent fraction for the following fraction?
3/6
1/4
1/2
1/3
Answers
Explanation:
Check out the diagram below. We have 3 pizza slices shaded out of 6 total to represent 3/6 of the entire thing. This is also 1/2 of the entire thing.
This is one visual way to see how 3/6 = 1/2.
You can multiply top and bottom of 1/2 to get 1*3 = 3 up top and 2*3 = 6 down below.
\(\frac{1}{2} = \frac{1*3}{2*3} = \frac{3}{6}\)

true or false: if you are given a graph with two shiftable lines, the correct answer will always require you to move both lines.
Answers
False. if you are given a graph with two shif table lines, the correct answer will always require you to move both lines.
In a graph with two shiftable lines, the correct answer may or may not require moving both lines. It depends on the specific scenario and the desired outcome or conditions that need to be met.
When working with shiftable lines, shifting refers to changing the position of the lines on the graph by adjusting their slope or intercept. The purpose of shifting the lines is often to satisfy certain criteria or align them with specific points or patterns on the graph.
In some cases, achieving the desired outcome may only require shifting one of the lines. This can happen when one line already aligns with the desired points or pattern, and the other line can remain fixed. Moving both lines may not be necessary or could result in an undesired configuration.
However, there are also situations where both lines need to be shifted to achieve the desired result. This can occur when the relationship between the lines or the positioning of the lines relative to the graph requires adjustments to both lines.
Ultimately, the key is to carefully analyze the graph, understand the relationship between the lines, and identify the specific criteria or conditions that need to be met. This analysis will guide the decision of whether one or both lines should be shifted to obtain the correct answer.
Learn more about graph from
https://brainly.com/question/19040584
#SPJ11
Help me please and thank you!!!

Answers
Answer:
f(3) = - 60
Step-by-step explanation:
To evaluate f(3) substitute x = 3 into f(x), that is
f(3) = 5(3)² - 7(4(3) + 3)
= 5(9) - 7(12 + 3)
= 45 - 7(15)
= 45 - 105
= - 60
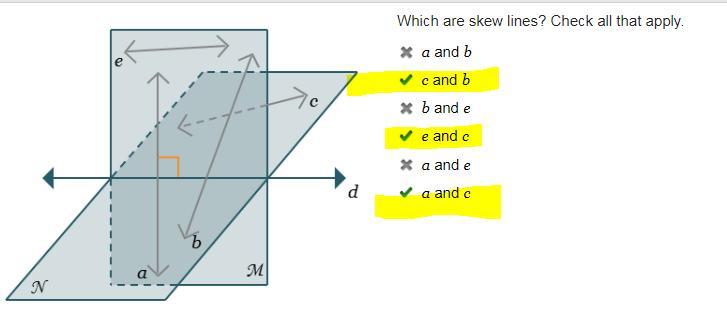
Which are skew lines? Check all that apply. a and b c and b b and e e and c a and e a and c
Answers
Answer:
c and b, e and c, a and c
Step-by-step explanation:
I just got them right, trust me;)
Answer:
Step-by-step explanation:
Consider the equation (x - 2)^2 - In x = 0. Find an approximation of it's root in [1, 2] to an absolute error less than 10^-9 with one of the methods covered in class.
Answers
The interval [1, 2] to an absolute error less than 10⁻⁹ is 1.46826171875.We have to find the approximate value of the root of this equation in the interval [1, 2] to an absolute error less than 10⁻⁹ using the methods
We will use the Bisection Method to solve the given equation as it is a simple and robust method. The Bisection Method: The bisection method is based on the intermediate value theorem, which states that if a function ƒ(x) is continuous on a closed interval [a, b], and if ƒ(a) and ƒ(b) have different signs, then there exists a number c between a and b such that ƒ(c) = 0.
The bisection method iteratively shrinks the interval [a, b] to the desired precision until we find an approximate root of the equation. The algorithm of the bisection method is as follows Choose an interval [a, b] such that ƒ(a) and ƒ(b) have opposite signs. We will use the above algorithm to solve the given equation.
Let a = 1 and b = 2 be the initial guesses.
Then, we can check whether ƒ(a) and ƒ(b) have opposite signs:
To know more about equation visit:
https://brainly.com/question/29657983
#SPJ11
Find the algebraic fraction of x3y-2x2y2/2xy3-x
2y2
Answers
After factoring out the common term of xy from the numerator and denominator, the given algebraic fraction simplifies to \((x^2 - 2xy) / [(2y - x) y]\).
The given algebraic fraction is:
\((x^3y - 2x^2y^2) / (2xy^3 - x2y2)\)
To simplify the expression, we can factor out the common term of xy from both the numerator and denominator:
\((xy) (x^2 - 2xy) / (xy^2) (2y - x)\)
Now we can simplify further by canceling out the common factor of xy in the numerator and denominator:
\((x^2 - 2xy) / (2y - x) y\)
So the simplified form of the algebraic fraction is:
\((x^2 - 2xy) / (2y - x) y\)
To simplify an algebraic fraction, we want to find a way to write it in a form that is easier to work with. One common method is to factor out common terms in both the numerator and denominator. In this case, we can factor out xy from both the numerator and denominator, since it is a common factor in both.
Once we factor out xy, we can rewrite the algebraic fraction as:
\((xy) (x^2 - 2xy) / (xy^2) (2y - x)\)
Next, we can simplify further by canceling out the common factor of xy in the numerator and denominator. This leaves us with:
\((x^2 - 2xy) / (2y - x) y\)
Learn more about algebraic fraction here:
https://brainly.com/question/11875858
#SPJ4
.Given the following Venn diagram, find n[ A ∪ ( B ∩ C ) ].
a) 76
b) 78
c) 74
d) 79
e) 73
f) None of the above.
Answers
The answer is (f) None of the above.
How do we find n?We can use the inclusion-exclusion principle to find the cardinality of the set A ∪ (B ∩ C). The formula is:
n(A ∪ (B ∩ C)) = n(A) + n(B) + n(C) - n(B ∪ C) - n(A ∩ B ∩ C)
We are given the values of n(A), n(B), n(C), n(A ∩ B), n(B ∩ C), and n(C ∩ A) from the Venn diagram. We can use these values to find n(B ∪ C) and n(A ∩ B ∩ C) as follows:
n(B ∪ C) = n(B) + n(C) - n(B ∩ C)
n(A ∩ B ∩ C) = n(A) + n(B) + n(C) - n(A ∪ B) - n(B ∪ C) - n(C ∪ A) + n(A ∩ B ∩ C)
Substituting the values from the Venn diagram, we get:
n(B ∪ C) = 50 + 28 - 16 = 62
n(A ∩ B ∩ C) = 18 + 16 + 28 - 50 - 62 - 20 + 10 = 0
Therefore,
n(A ∪ (B ∩ C)) = n(A) + n(B) + n(C) - n(B ∪ C) - n(A ∩ B ∩ C) = 32 + 50 + 20 - 62 - 0 = 40
So the answer is (f) None of the above.
Learn more about Venn
brainly.com/question/20795347
#SPJ11
Which of the numbers below correctly represents (-1)17?
Answers
Answer:
Step-by-step explanation:
https://answer.ya.guru/questions/6481809-which-number-line-correctly-represents-the-irrational-numbers.html
Answer:
i dont know because you didnt give number but is one -17 is so its that
Step-by-step explanation:
Im give qs for my lil sis so she wants 16 x 5
Answers
Answer:
80
Step-by-step explanation:
16x5=80
Which property is shown in the matrix addition below?
5
-1
0
5
-7
0.4
0
-7
0
0.4
+
+
+
6.2
-8.5
-9.9
6.2
-9.9
-8.5
12
0
2
12
0
2
inverse property
identity property
commutative property
associative property
Help please!

Answers
Answer:
associative property
The solution is, property is shown in the matrix addition below is
associative property.
Here, we have,
The property shown in the given matrix addition is associative property.
Let's define associative property first,
The Associative Property of Addition for Matrices states :
Let A , B and C be m×n matrices .
Then, (A+B)+C=A+(B+C) .
Associative Law of Addition of Matrix:
Matrix addition is associative. This says that, if A, B and C are Three matrices of the same order such that the matrices B + C, A + (B + C), A + B, (A + B) + C are defined then A + (B + C) = (A + B) + C.
Since P and Q are of the same order and pij = qij then, P = Q.
Here, from the given information,
we get, A , B and C be 4×1 matrices,
and, (A+B)+C=A+(B+C)
So, The solution is, property is shown in the matrix addition below is
associative property.
To learn more on matrix click:
brainly.com/question/30646566
#SPJ7
: Question 4 Find an equation inx and y for the line tangent to the curve x(t)--, y(r)- at the point,10 2x + 20 10 46 1 56 2
Answers
The equation in x and y for the line tangent to the curve x(t) = 10t + 46 and y(t) = 2t² + 20t + 56 at the point (10, 46).
By finding the derivatives of x(t) and y(t) with respect to t, we can determine the slope of the tangent line at any given point. Plugging in the value of t corresponding to the point (10, 46) into the derivatives will give us the slope of the tangent line at that point. Finally, using the point-slope form of a linear equation, we can write the equation of the tangent line in terms of x and y.
To find the equation of the line tangent to the curve x(t) = 10t + 46 and y(t) = 2t² + 20t + 56 at the point (10, 46), we need to determine the slope of the tangent line at that point. We start by finding the derivatives of x(t) and y(t) with respect to t.
The derivative of x(t) with respect to t gives us the rate of change of x with respect to t, which is the slope of the tangent line for the x-coordinate. Taking the derivative of x(t) = 10t + 46, we get dx/dt = 10.
The derivative of y(t) with respect to t gives us the rate of change of y with respect to t, which is the slope of the tangent line for the y-coordinate. Taking the derivative of y(t) = 2t² + 20t + 56, we get dy/dt = 4t + 20.
To find the slope of the tangent line at the point (10, 46), we substitute t = 10 into the derivatives: dx/dt = 10 and dy/dt = 4(10) + 20 = 60.
Now that we have the slope (m) of the tangent line, we can use the point-slope form of a linear equation: y - y1 = m(x - x1), where (x1, y1) represents the given point on the curve. Substituting (10, 46) and the slope m = 60, we get the equation of the tangent line:
y - 46 = 60(x - 10)
Simplifying the equation further, we have:
y - 46 = 60x - 600
This is the equation in x and y for the line tangent to the curve x(t) = 10t + 46 and y(t) = 2t² + 20t + 56 at the point (10, 46).
Learn more about Tangent:
brainly.com/question/10053881
#SPJ11
Let X (3, 0.02). Given Tx = 300 calculated by the Esscher Premium Principle with parameter 1, calculate h
Answers
The value of h is 99.969.
The Esscher Premium Principle is a method of calculating insurance premiums that considers the risk of an event occurring and the potential severity of the loss. The formula for the Esscher Premium Principle is:
Ex = ln(∑eαx Px)/α
Where Ex is the Esscher premium, α is the parameter, x is the loss amount, and Px is the probability of the loss occurring.
In this case, we are given X (3, 0.02), meaning that the loss amount is 3 and the probability of the loss occurring is 0.02. We are also given that the Esscher premium is 300 and the parameter is 1. Plugging these values into the formula, we get:
300 = ln(∑e1(3) 0.02)/1
Simplifying the equation, we get:
300 = ln(0.02e3)
Taking the natural logarithm of both sides, we get:
e300 = 0.02e3
Dividing both sides by 0.02, we get:
e300/0.02 = e3
Taking the natural logarithm of both sides again, we get:
300 - ln(0.02) = 3
Solving for h, we get:
h = (300 - ln(0.02))/3
h = 99.969
Therefore, the value of h is 99.969.
To know more about Esscher Premium Principle, refer here:
https://brainly.com/question/29412050#
#SPJ11
1. pick out the well defined set from the following 1 a = ( test cricket captains of pakistan 2 b = ( tasty food items)
Answers
The well defined set is a = ( test cricket captains of pakistan).
What is a well defined set?A set which is composed of elements which have finite value and does not depend upon the nature of thinking of different persons is called well defined set.
Some key features regarding the set are-
A set is a collection of specific things or a group of specific objects in mathematics. The set theory created by George Cantor is currently applied in all disciplines of mathematics. 'A set is a well-defined collection of separate things of our sense or cognition, to be considered as a whole,' he says.A hard definition of a set is not conceivable, as it is not possible for the ideas of geometrical point, line, and plane. Is the intuitive perception of a gathering or aggregation of real or mental items.The following are some examples of basic set concepts:
a group of current Australian cricketers. a collection of regulations for playing badminton; a set of integers subject to specified conditions; a collection of books from the library; a group of American states;To know more about well defined set, here
https://brainly.com/question/18775887
#SPJ4
Use the function: g(x) = (x + 2)(x - 1)(x - 2) a) Find the zeros of the function. b) Find the y-intercept of the function.
Answers
Answer:
The zeros are -2, 1, and 2
Step-by-step explanation:
You have to set each individual equation equal to zero.
ex: (x+2) x+2=0 move the number to the right hand side to get x alone x=-2
as for the y intercept I don't know
Answer:
see explanation
Step-by-step explanation:
g(x) = (x + 2)(x - 1)(x - 2)
To find the zeros let g(x) = 0 , then
(x + 2)(x - 1)(x - 2) = 0
Equate each factor to zero and solve for x
x + 2 = 0 ⇒ x = - 2
x - 1 = 0 ⇒ x = 1
x - 2 = 0 ⇒ x = 2
The zeros are x = - 2, x = 1, x = 2
To find the y- intercept substitute x = 0 into g(x)
g(0) = (0 + 2)(0 - 1)(0 - 2) = 2(- 1)(- 2) = 2 × 2 = 4
The y- intercept is 4 or (0, 4 )
If sin theta <0 and tan theta >0 then:
Answers
Answer:
Step-by-step explanation:
If the sine is negative then theta must be in Quadrant III or Quadrant IV.
If the tangent is positive then theta must be in Quadrant I or III.
If both conditions must be satisfied, then we conclude that thera is in Quadrant III.
Note that \(\tan\theta=\frac{\sin\theta}{\cos\theta}.\) Thus, if \(\sin\theta<0\) and \(\tan\theta>0,\) then we must have \(\cos\theta<0\) as well. The sine function is negative when \(\theta\) lies in Quadrant III or IV, and the cosine function is negative when \(\theta\) lies in Quadrant II or III. Thus, the two are both negative when \(\theta\) lies in Quadrant III, or \(\pi+2\pi n<\theta<\frac{3\pi}{2}+2\pi n\) for integer values of \(n.\)
The following data show the frequency of rainy days in a year less than 0.01 inch 165 days 0.01 -1 inch 90 days 1.01 - 5 inches 60 days 5.01 -10 inches 40 days more than 10 inches 10 days Find the mode.
Answers
The mode of a dataset is the value that appears most frequently. In this case, we need to find the interval of rainfall that occurs most frequently.
From the given data, we can see that the interval "less than 0.01 inch" has the highest frequency with 165 days. Therefore, the mode of this dataset is "less than 0.01 inch"
Effective communication is crucial in all aspects of life, including personal relationships, business, education, and social interactions. Good communication skills allow individuals to express their thoughts and feelings clearly, listen actively, and respond appropriately. In personal relationships, effective communication fosters mutual understanding, trust, and respect.
In the business world, it is essential for building strong relationships with clients, customers, and colleagues, and for achieving goals and objectives. Good communication also plays a vital role in education, where it facilitates the transfer of knowledge and information from teachers to students.
Moreover, effective communication skills enable individuals to engage in social interactions and build meaningful connections with others. Therefore, it is essential to develop good communication skills to succeed in all aspects of life.
Learn more about dataset here:
https://brainly.com/question/26468794
#SPJ11
Consider the function y=30e −x 2/3 Follow the steps to find dtdy.a. Determine what the inside and outside functions are Let the insides be the variable u, then rewrite y in terms of u : Insides u= Outside y= b. Use the chain rule to find the derivative of the function. Write your answer in termsof x.
Answers
The derivative of y = 30e^(-x^(2/3)) with respect to x is dy/dx = 30e^(-x^(2/3)) * -(2/3)x^(-1/3).
The inside function is u = -x^(2/3), and the outside function is y = 30e^u. Rewrite y in terms of u: y = 30e^(-x^(2/3)).
To find dy/dx using the chain rule, we need to differentiate the outside function with respect to the inside function (u) and then multiply it by the derivative of the inside function with respect to x. Applying the chain rule, we have:
dy/du = 30e^u (derivative of the outside function with respect to u)
du/dx = -(2/3)x^(-1/3) (derivative of the inside function with respect to x)
Now we can multiply these two derivatives together to find dy/dx:
dy/dx = dy/du * du/dx = 30e^u * -(2/3)x^(-1/3)
Substituting u = -x^(2/3) into the equation, we get:
dy/dx = 30e^(-x^(2/3)) * -(2/3)x^(-1/3)
Therefore, the derivative of y = 30e^(-x^(2/3)) with respect to x is dy/dx = 30e^(-x^(2/3)) * -(2/3)x^(-1/3).
a. In the function y = 30e^(-x^(2/3)), the inside function is -x^(2/3) denoted as u, and the outside function is y = 30e^u.
b. To differentiate the function using the chain rule, we start by finding the derivative of the outside function with respect to the inside function, which is dy/du = 30e^u. Then, we find the derivative of the inside function with respect to x, du/dx = -(2/3)x^(-1/3). Finally, we multiply these two derivatives together to obtain the derivative of the entire function with respect to x, which is dy/dx = 30e^(-x^(2/3)) * -(2/3)x^(-1/3).
To learn more about derivative click here
brainly.com/question/25324584
#SPJ11
Найдите значение выражения x − 3(х + 8) при x = −10.
Answers
Answer:
-4
Step-by-step explanation:

The first two steps in determining the solution set of the system of equations, y = x2 – 6x + 12 and y = 2x – 4, algebraically are shown in the table.
Which represents the solution(s) of this system of equations?
(4, 4)
(–4, –12)
(4, 4) and (–4, 12)
(–4, 4) and (4, 12)

Answers
Answer:
(4,4)
Step-by-step explanation:
The solution set of the system of equations can be found by setting the two equations equal to each other and solving for x.
x^2 - 6x + 12 = 2x - 4
x^2 - 8x + 16 = 0
(x - 4)^2 = 0
x = 4
Since both equations in the system are equal to y, we can substitute x = 4 into either equation to find the corresponding value of y.
y = 2x - 4 = 2(4) - 4 = 4
Therefore, the solution of this system of equations is (4, 4).
Therefore, the correct answer is (4, 4).
Write the measure in descending order 0.5m - 480mm - 55cm
Answers
Answer:
480mm<55cm<0.5m
Step-by-step explanation:
millimeters means 100
centimeters means 10
meters means 1
there are 10mm in every 1cm and 100cm in every 1m
Answer:
55cm>0.5m>480mm
Step-by-step explanation:
as we know
1000mm=1m
100cm=1m
So we see
55=55cm
0.50=50cm
480=48cm
Hope it helps you thanks
Please mark as The Brainlist
Thank you
Let d be the number of dollars you spent on gas and let g be the number of gallons you purchased. Which expression represents the price you paid per gallon?
Answers
Answer:
The expression represents the price you paid per gallon is:
Price paid per gallon = \(\frac{d}{g}\)Step-by-step explanation:
To identify the expression is right, I'll show you with an example: suppose that you paid $56 buying 7 gallons of gas, now you can replace those values in the expression I gave you:
Price paid per gallon = \(\frac{d}{g}\)Price paid per gallon = \(\frac{56}{7}\)Price paid per gallon = 8And you can check this value by multiplying the price paid by the gallon and the number of gallons, which you obtain the number of dollars you spent:
Number of dollars (d) = 8 * $7 = $56Please help me with this homework

Answers
Answer:
Option D: \(y= -\frac34x+14\)
Step-by-step explanation:
In order for two lines to be perpendicular, the product of the slopes has to be \(-1\). That allows you to rule out A and C. Let's plug the coordinate of the point in B. If the equality holds, we found or line. Else, it's D.
\(11 =-\frac34(4) +8 \rightarrow 11 = -3+8 \rightarrow 11=5\) Which is obviously impossible. Our line has to be D
solve for x.
a) 9\(9^{3x+4}\) = \(27^{4x+3}\)
b) \(4^{3x}\) = \(2^{x+1}\)
(include steps pleez)
Answers
Answer:
Question a)
\(9^{3x+4}=27^{4x+3}\)
\(x=-0.166\)
Question b)
\(4^{3x}=2^{x+1}\)
\(x=0.2\)
Step-by-step explanation:
Question a)
Given the expression
\(9^{3x+4}=27^{4x+3}\)
Taking log on both sides
\(log\left(9^{3x+4}\right)=log\left(27^{4x+3}\right)\)
\(\left(3x+4\right)\cdot \left(log\left(9\right)\right)\:=\left(4x+3\right)\cdot \left(log\left(27\right)\right)\)
\(3x+4=\left(\frac{log\left(27\right)}{log\left(9\right)}\right)\cdot \left(4x+3\right)\)
\(3x+4=1.5\times \left(4x+3\right)\)
\(3x+4=6x+4.5\)
\(3x=6x+0.5\)
\(\frac{-3x}{-3}=\frac{0.5}{-3}\)
\(x=-0.166\)
Therefore, the value of x:
\(x=-0.166\)
Question b)
Similarly, we can solve the 'b' expression
Given the expression
\(4^{3x}=2^{x+1}\)
Taking log on both sides
\(log\left(4^{3x}\right)=log\left(2^{x+1}\right)\)
\(3x\cdot \left(log\left(4\right)\right)=\left(x+1\right)\cdot \left(log\left(2\right)\right)\)
\(3x=\left(\frac{log\left(2\right)}{log\left(4\right)}\right)\cdot \left(x+1\right)\)
\(3x=0.5\times \left(x+1\right)\)
\(3x=0.5x+0.5\)
\(2.5x=0.5\)
Divide both sides by 2.5
\(\frac{2.5x}{2.5}=\frac{0.5}{2.5}\)
\(x=0.2\)
Therefore, the value of x = 0.2
Find the value of 125^2/3
Answers
Answer: 5208.3
Step-by-step explanation:
125^2/3
15625/3
5208.33333333
5208.3
3.
(i) Show that t(n + 1) = n t(n).
(ii) Find t(2), (3) and T() if given t(1) = 1,T()= √π.
Given a differential equation below where p is a constant.
(1 - x²)y" - 2xy' +p(p+1)y = 0.
(i) Determine the singular point and the ordinary point for the differential equation above.
Go Premium
&
(b) Usng the values of a; obtained in 1 (a), solve the initial value problem below: (+ a₁ay + αoy = 2(1 + ex)
where y(0) = 4,y'(0) = 2,y" (0) = 2.
The Legendre polynomials P (x) are defined by Po (x) = 1 and 1 1 d Pn(x) = (x²-n)", n = 1,2,3,...
(1) Verify that P(x)=(3x-1) and P(x)=(5x-3x).
(ii) For k = 0,1,...,n-1, show that x* P(x)dx = 0.
2.
Answers
The given statement is proven below:
(i) t(n + 1) = n t(n)
(ii) t(2) = 2t(1), t(3) = 3t(2), T() = √π
(i) To show that t(n + 1) = n t(n), we can use mathematical induction.
First, we establish the base case: t(2) = 2t(1). This is given in the problem statement.
Next, we assume that the equation holds for some arbitrary value k: t(k + 1) = k t(k).
Now, we need to prove that it holds for k + 1 as well: t((k + 1) + 1) = (k + 1) t(k + 1).
Using the recursive definition of t(n), we can rewrite the equation as t(k + 2) = (k + 1) t(k + 1).
Expanding t(k + 2) using the recursive definition, we have t(k + 2) = (k + 2) t(k + 1).
Since (k + 2) is equal to (k + 1) + 1, we can substitute it into the equation.
This gives us (k + 2) t(k + 1) = (k + 1) t(k + 1), which simplifies to t(k + 2) = (k + 1) t(k + 1).
Therefore, the equation t(n + 1) = n t(n) holds for all positive integers n.
(ii) To find the values of t(2), t(3), and T(), we can use the given initial conditions.
We are given that t(1) = 1. Using the recursive definition, we can find t(2) = 2t(1) = 2(1) = 2.
Similarly, t(3) = 3t(2) = 3(2) = 6.
Finally, we are given that T() = √π.
Learn more about mathematical induction
brainly.com/question/29503103
#SPJ11
Solve pls brainliest

Answers
WHY? They all equal 0.5.