( Trig. Functions and Angles of Elevation & Depression)
A spotlight (which is mounted at ground level) is pointing to the top of the Empire State Building with an angle of elevation of 78°
. If the horizontal (along the ground) distance between the building and the spotlight is is 309 feet, how tall is the Empire State Building?
Answers
Answer:
To solve this problem, we can use trigonometric functions and the concept of angles of elevation and depression.
Let's first define the terms "angle of elevation" and "angle of depression". An angle of elevation is the angle between a horizontal line and a line from the observer's eye to an object above the horizontal line. An angle of depression is the angle between a horizontal line and a line from the observer's eye to an object below the horizontal line.
In this problem, we are given that the angle of elevation from the spotlight to the top of the Empire State Building is 78°. We can use this information to find the height of the building.
X represents the point where the spotlight hits the Empire State Building. We want to find the height of the building, which we can call h.
We know that tan(78°) = h/309. To solve for h, we can multiply both sides by 309:
h = 309 * tan(78°)
Using a calculator, we get:
h ≈ 1289.5 feet
Therefore, the Empire State Building is approximately 1,289.5 feet tall.
Related Questions
In Isaiah’s class, 18/24 of the students like swimming better than they like running. What is 18/24 in simplest form?
Answers
Answer:
3/4
Step-by-step explanation:
Give triangle ABC with coordinates A(3, 8), B(9,0) and C(5,2). How can you prove that triangle ABC is isosceles? Show your work.
Answers
Answer:
The distances AB and BC are
√
52
and therefore isosceles.
Explanation:
If we label them A(13,-2) B(9-8) and C(5-2)
The distance between A and B:13⇒9=4−2⇒−8=42+62=52 so the distance is √52
The distance between B and c:9⇒5=4−8⇒−2=642+62=52
the distance is
√
52
The distance between A and C is 8 as they are both on -2 for
y
The distances AB and BC are
√
52
and therefore isosceles.Step-by-step explanation:
The gross domestic product (GDP) of the United States is defined as
Answers
Answer:
the market value of all final goods and services produced within the United States in a given period of time.
Has anyone done the inverse functions mastery text on edmentum it’s super hard stuck on this question and the pictures wont help
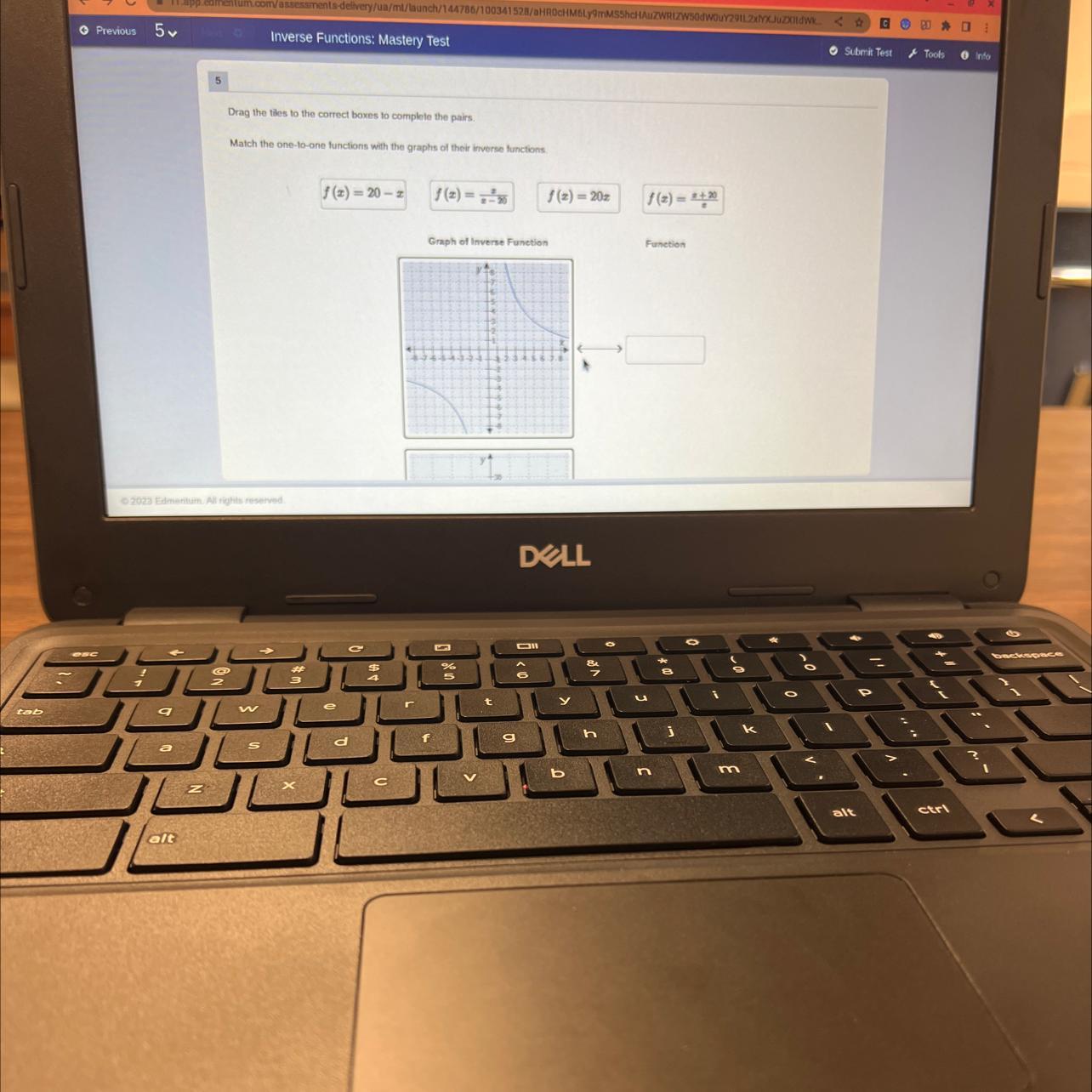
Answers
Which graph represents 12 = 3x + 4y line a, line b, line c

Answers
Answer:
green line or "b"
Step-by-step explanation:
we can set this up into the slope intercept form
y=mx+b
where m is the slope and b is y intercept
12=3x+4y
-3x -3x
-3x+12=4y
/4. /4. /4
-3/4x+3=y
we can see the only line with a negative slope and a y intercept at 3 is the green line or "b"
hopes this helps please mark rainliest
Howard buys 5 suits a year when he earns $70,000. When his income increases to $200,000, he buys 15 suits a year. Based on this
information, suits are considered to be
a complementary good.
an inferior good.
a neutral good.
a normal good.
a substitute good.
Answers
Answer:
a complementary good
Step-by-step explanation:
Howard spends $70,000 per year on 5 suits. When his income reaches $200,000, he purchases 15 suits per year. Suits are classified as a normal good based on this information.
What is meant by Normal Good?A normal good is one that sees an increase in demand due to an increase in consumer income. In other words, an increase in wages leads to an increase in demand for ordinary goods, whereas a decrease in wages or layoffs leads to a decrease in demand. In economics, an inferior good is one whose demand falls when consumer income rises (or rises when consumer income falls), as opposed to normal goods, which experience the opposite effect. Normal goods are those whose demand increases as consumer income rises. Normal goods are those for which the relationship between consumer income and quantity demanded is positive. In other words, the income effect is positive while the substitution effect is negative.To learn more about normal good, refer to:
https://brainly.com/question/12671549
#SPJ2
PLEASE HELP ITS MATH THANK YOUUUU

Answers
Show that each of these conditional statements is a tautology by using truth tables: (a) ¬p→(p→q)

Answers
Find f(g(x)) and g(f(x)) and determine whether the pair of functions f and g are inverses of each other.f(x) = 8x-2 and g(x) = x+8/2a. f(g(x)) =
Answers
The fuction f(g(x)) is given by
\(\begin{gathered} \text{f(g(x))}=f(\frac{x+8}{2}) \\ =8(\frac{x+8}{2})-2 \\ =4(x+8)-2 \\ =4x+32-2 \\ =4x+30 \end{gathered}\)The function g(f(x)) is
\(\begin{gathered} g(f(x))=g(8x-2) \\ =\frac{(8x-2)-2}{2} \\ =\frac{8x-4}{2} \\ =4x-2 \end{gathered}\)The functions f and g will be inverses of each other if the function values obtained is x in both cases. But, we got 4x+30 for f(g(x) and 4x-2 for g(f(x)), which are not equal to x. So, f and g are not inverses of each other.
Find the volume of a right circular cone that has a height of 11.7m and a base with a circumference of 9 m.
Answers
Answer: Approximately 25.1 m^3
Step-by-step explanation:
The volume of a cone is \(V=\pi r^2\frac{h}{3}\). We know the height, but we don't know the radius. Fortunately, we are given the circumference of the base circle.
\(C=2\pi r\)
\(9=2\pi r\)
\(r=\frac{9}{2\pi}\)
Now that we have the r, we can plug it into the volume equation.
\(V=\pi r^2\frac{h}{3}\)
\(V=\pi (\frac{9}{2\pi } )^2 (\frac{11.7}{3} )\)
After you plug this into the calculator, you get approximately 25.1 m^3.
Only answer if you’re sure :) need the whole answer! Will give Brainly

Answers
Answer:
Step-by-step explanation:
y = -1x + 1
y = -x + 1
I'm sure :P
Answer:
y=-1x+1
Step-by-step explanation:
the slope is 1/1 and line is declining hence the negative
what are these questions



Answers
The gradient of y = 16 - 8x is - 8
The gradient of y - 5 = 6x is 6
y = mx + c form of y - 5 = 6x is
What is Gradient:
The slope is another name for the gradient. Any straight line's gradient illustrates or demonstrates how steep it is. The gradient is said to be bigger if any line is steeper.
In other words, the ratio of vertical change to horizontal change is known as Gradient.
The gradient of line y = mx + c is 'm'
Here we have
Equation (1) y = 16 - 8x
Compare the given equation with y = mx + c
=> Gradient / Slope (m) = - 8
Equation (2) y = 7x + 8
Compare the given equation with y = mx + c
=> Gradient/ Slope (m) = 7
Equation (3) y - 5 = 6x
Convert the given equation in the form of y = mx + c
=> y - 5 = 6x
Add 5 on both sides
=> y = 6x + 5
When we compare the given equation with y = mx + c
=> Gradient / Slope (m) = 6
Therefore,
The gradient of y = 16 - 8x is - 8
The gradient of y - 5 = 6x is 6
y = mx + c form of y - 5 = 6x is y = 6x + 5.
Learn more about Gradient at
https://brainly.com/question/11693181
#SPJ1
Determine the growth defined by the equation y=1.4(3.72)^x.
Answers
Answer:
the type of growth defined by the equation is Exponential growth.
Step-by-step explanation:
Exponential growth :-Exponential growth is a pattern of data that shows greater increases with passing time, creating the curve of an exponential function. It occurs when the instantaneous rate of change of a quantity with respect to time is proportional to the quantity itself
expression for exponential growth -
f(x) = k(1+t)^x
f(x) = exponential growth
k = initial amount
t = rate of growth
x = no of time interval
therefor,
the equation shown in the question represents exponential growth with increasing time.
hence, Exponential growth is the correct answer.
learn more about exponential growth at :
https://brainly.com/question/11487261
#SPJ10
help me solve this queston

Answers
TJohn's age is approximately 23.33 years, and Sharon's age is approximately 93.33 years.
And the correct graph is D.
To represent the given problem as a system of equations, we can use the following information:
John is 70 years younger than Sharon: j = s - 70
Sharon is 4 times as old as John: s = 4j
Let's plot the graph for this system of equations:
First, let's solve equation (2) for s:
s = 4j
Now substitute this value of s in equation (1):
j = s - 70
j = 4j - 70
3j = 70
j = 70/3
Substitute the value of j back into equation (2) to find s:
s = 4j
s = 4(70/3)
s = 280/3
The solution to the system of equations is j = 70/3 and s = 280/3
In the graph d, the solution to the system of equations is represented by the point (70/3, 280/3), which is approximately (23.33, 93.33) on the graph.
Therefore, John's age is approximately 23.33 years, and Sharon's age is approximately 93.33 years.
And the correct graph is D.
Learn more about system of equations click;
https://brainly.com/question/20067450
#SPJ1

Which is larger 64 inches or 5 feet
Answers
Answer:
64 inches
Step-by-step explanation:
There are 12 inches in a foot
12 x 5 is 60
64 is greater then 60
araceli renta un local rectangular de 4.2 metros de frente y 7.3 metros de largo para su panaderia, ¿cuantos metros cuadrados tiene el local que rento?
Answers
The number of square meters that the space that Araceli rents is, is 30. 66 square meters.
How to find the area ?The space that Araceli rents has a rectangular space so to find the area of the rectangular space that Araceli rents, we need to multiply the length by the width.
The given width is 4. 2 meters and the length is 7. 3 meters.
The area of the space in square meters is therefore :
Area = Length × Width
Area = 7. 3 meters × 4. 2 meters
Area = 30. 66 square meters
In conclusion, the space that Araceli rents has an area of 30. 66 square meters.
Find out more on area at https://brainly.com/question/2129070
#SPJ1
Can the following lengths be
used to form a right triangle?
Explain.
Length 1: 15 units
Length 2: 20 units
Length 3: 35 units
Answers
Of 82 adults selected randomly from one town 66 have healthcare find a 90% confidence interval for the true proportion of all adults in the town who have health insurance.
Answers
The 90% confidence interval for the true proportion of all adults in the town who have health insurance is approximately 0.7294 to 0.8804.
How to find the 90% confidence interval for the true proportion of all adults in the town who have health insuranceUsing the formula for calculating a confidence interval for a proportion.
The formula for the confidence interval is:
Confidence Interval = Sample proportion ± Margin of error
where:
Sample proportion = Number of adults with health insurance / Total sample size
Margin of error = Critical value * Standard error
The critical value depends on the desired confidence level. For a 90% confidence level, the critical value can be obtained from the standard normal distribution table, which corresponds to a Z-value of 1.645.
The standard error can be calculated using the formula:
Standard error =\(\sqrt{} ((p * (1 - p)) / n)\)
Given:
Number of adults with health insurance (sample proportion) = 66
Total sample size = 82
Confidence level = 90%
Now, let's calculate the confidence interval:
Sample proportion = 66 / 82 ≈ 0.8049
Standard error = \(\sqrt{}\)((0.8049 * (1 - 0.8049)) / 82) ≈ 0.0459
Margin of error = 1.645 * 0.0459 ≈ 0.0755
Lower bound of the confidence interval = Sample proportion - Margin of error ≈ 0.8049 - 0.0755 ≈ 0.7294
Upper bound of the confidence interval = Sample proportion + Margin of error ≈ 0.8049 + 0.0755 ≈ 0.8804
Therefore, the 90% confidence interval for the true proportion of all adults in the town who have health insurance is approximately 0.7294 to 0.8804.
Learn more about confidence interval at https://brainly.com/question/20309162
#SPJ1
Find the value of 3a when a = -4.
(b)- 7
(d) -12
(a) 7
(c) 12
Answers
Answer:
(d) -12
Step-by-step explanation:
3a = _____
a = -4
3(-4) = ___
3(-4) = -12
The answer is (d) -12
Use the square roots property to solve the quadratic equation If there are multiple answers, list them separated by a comma, e.g. 1,2. If there is no solution, enter ∅.

Answers
The quadratic equation is given as
\((y+\frac{1}{3})^2=81\)Using the square roots property, we need to find the square root of both sides.
Therefore, we get
\(y+\frac{1}{3}=\pm\sqrt[]{81}\)Hence, we can solve as
\(\begin{gathered} y+\frac{1}{3}=\pm9 \\ y=\pm9-\frac{1}{3} \end{gathered}\)The roots can be gotten as
\(\begin{gathered} y=9-\frac{1}{3} \\ y=8\frac{2}{3} \end{gathered}\)or
\(\begin{gathered} y=-9-\frac{1}{3} \\ y=-9\frac{1}{3} \end{gathered}\)The answer is
\(y=8\frac{2}{3},-9\frac{1}{3}\)PRE CALC HELP NEEDED

Answers
Answer:
\(\dfrac{5e^2}{2}\)
Step-by-step explanation:
Differentiation is an algebraic process that finds the slope of a curve. At a point, the slope of a curve is the same as the slope of the tangent line to the curve at that point. Therefore, to find the slope of the line tangent to the given function, differentiate the given function.
Given function:
\(y=x^2\ln(2x)\)
Differentiate the given function using the product rule.
\(\boxed{\begin{minipage}{5.5 cm}\underline{Product Rule for Differentiation}\\\\If $y=uv$ then:\\\\$\dfrac{\text{d}y}{\text{d}x}=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}$\\\end{minipage}}\)
\(\textsf{Let\;$u=x^2}\)\(\textsf{Let\;$u=x^2$}\implies \dfrac{\text{d}u}{\text{d}x}=2x\)
\(\textsf{Let\;$v=\ln(2x)$}\implies \dfrac{\text{d}v}{\text{d}x}=\dfrac{2}{2x}=\dfrac{1}{x}\)
Input the values into the product rule to differentiate the function:
\(\begin{aligned}\dfrac{\text{d}y}{\text{d}x}&=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}\\\\&=x^2 \cdot \dfrac{1}{x}+\ln(2x) \cdot 2x\\\\&=x+2x\ln(2x)\end{aligned}\)
To find the slope of the tangent line at x = e²/2, substitute x = e²/2 into the differentiated function:
\(\begin{aligned}x=\dfrac{e^2}{2}\implies \dfrac{\text{d}y}{\text{d}x}&=\dfrac{e^2}{2}+2\left(\dfrac{e^2}{2}\right)\ln\left(2 \cdot \dfrac{e^2}{2}\right)\\\\&=\dfrac{e^2}{2}+e^2\ln\left(e^2\right)\\\\&=\dfrac{e^2}{2}+2e^2\\\\&=\dfrac{5e^2}{2}\end{aligned}\)
Therefore, the slope of the line tangent to the graph of y = x²ln(2x) at the point where x = e²/2 is:
\(\boxed{\dfrac{5e^2}{2}}\)
Olive has a plastic container shaped like a cube to put slime in. She measures one side and finds that it’s 0.5 foot long. Use the formula V = s3 to determine how many cubic feet of slime will fit in her container. PLEASE HELP!
Answers
Answer:
0.125 cubic feet
Step-by-step explanation:
Since the container has a shape of a cube with a measure of its side 0.5 ft, then;
Volume of the container, V = \(s^{2}\)
where s is the measure of its side.
s = 0.5 ft, then;
V = \((0.5)^{3}\)
= 0.125
V = 0.125 cubic feet
The cubic feet of slime that would fit in the container is 0.125.
A biker traveled 2/5 of the road on the first day, then traveled 5 kilometers less on the next day, which is equal to 3/8 of the road. How much more does he need to travel? (distance)
Answers
The biker needs to travel 45 km more to complete his journey.
Given that, a biker traveled 2/5 of the road on the first day, then traveled 5 kilometers less on the next day, which is equal to 3/8 of the road, we need to find how much he need to cover more,
Let the total distance of the road be x,
So,
2x/5 - 5 = 3x/8
2x/5 - 3x/8 = 5
Solving for x,
Multiply by 40 to both sides,
16x-15x = 200
x = 200
Therefore, the total distance of the road is 200 km.
Since, he travelled =
200 (2/5) = 80 km + 200 (3/8) = 75 km = 155 km
Therefore, he needs to travel 200-155 = 45 km more.
Hence, the biker needs to travel 45 km more to complete his journey.
Learn more about equations, click;
https://brainly.com/question/29657983
#SPJ1
how many balls are there in ten dozen
Answers
Answer:
120 balls
Step-by-step explanation:
Ten dozen is 120.
Which of the following random variables are discrete?
I. L= the number of pages in a randomly selected book
II. A = the number of leaves on a randomly selected tree
III. K= the height of a randomly selected NBA player
a. I only
I and II
b. II and III
c. II and III
d. l,ll, lll
Answers
Answer:
Step-by-step explanation:
I and II
Pages in a book and leaves on a tree can be counted precisely. They are discrete.
The height of a person cannot be measured exactly. We can get very good
approximations (to a lot of decimal places) but never exact. This is continuous.
What are the important variables in the problem below?
A test is worth 80 points. Multiple-choice questions are worth 2 points, and
short-answer questions are worth 4 points. If the test has 25 questions, how
many multiple-choice questions are there?
OA. p for points, m for multiple choice
OB. s for short answer, t for test
OC. m for multiple choice, s for short answer
OD. t for test, q for questions
Answers
The important variables are the two types of test questions which can be represented as :
m for multiple choice, s for short answerVariables are used to represent unknown values which could be worked out in a mathematical expression or problem.
The variables or unknown in this case are the type of test questions. which are : m for multiple choice, s for short answer
Therefore, the correct option is C. m for multiple choice, s for short answer
Learn more on word problems:https://brainly.com/question/25693822
#SPJ1
What is the end behavior of the graph of f(x) = x5 - 8x4 + 16x³?
O
O f(x)→→∞ as x→∞; f(x) →→∞ as x→ +∞
f(x)→∞ as x→-∞0; f(x) → +∞o as x→ +∞
O f(x) +∞o as x→-∞; f(x) →→→∞as x→ +∞
+∞o as x→∞0; f(x)→ +∞ as x→→ +00
O
f(x)
DONE
Answers
The end behaviour of the graph of f(x) \(=\) x⁵ - 8x⁴ \(+\) 16x³ is f(x)→∞ as x→∞; f(x) →-∞ as x→ -∞ , the correct option is (a) .
In the question ,
it is given that ,
the function is f(x) \(=\) x⁵ - 8x⁴ \(+\) 16x³ ,
In the function as x approaches -∞ , x⁵ will also approach -∞ , because negative number raised to the odd power , gives a negative result .
In the function as x approaches ∞ , x⁵ will also approach ∞ , because positive number raised to the odd power , gives a positive result .
that is f(x)→∞ as x→∞; f(x) →-∞ as x→ -∞
let us find the roots of the function ,
f(x) \(=\) 0
x⁵ - 8x⁴ \(+\) 16x³ = 0
taking x³ common ,
x³(x² - 8x \(+\) 16) = 0
x³(x² - 4x - 4x + 16) = 0 .... by using splitting the middle term method
x³(x(x - 4) - 4(x - 4)) = 0
x³(x - 4)(x - 4) = 0
which means x³ \(=\) 0 and x-4 = 0
that is x=0 and x = 4 .
So , the roots of the function f(x) are x=0 and x=4 .
This means that the graph has a repeated root and so it will touch the x-axis but not at the repeated root of x \(=\) 4.
Therefore , The end behaviour of the graph of f(x) \(=\) x⁵ - 8x⁴ \(+\) 16x³ is f(x)→∞ as x→∞; f(x) →-∞ as x→ -∞ , the correct option is (a) .
The given question is incomplete , the complete question is
What is the end behavior of the graph of f(x) = x⁵ - 8x⁴ + 16x³ ?
(a) f(x)→∞ as x→∞; f(x) →-∞ as x→ -∞
(b) f(x)→∞ as x→-∞0; f(x) → +∞ as x→ +∞
(c) f(x)→∞ as x→ -∞; f(x) →-∞ as x→ +∞
(d) f(x)→-∞ as x→∞ ; f(x)→ -∞ as x→∞
Learn more about Function here
https://brainly.com/question/12682603
#SPJ1
Rounded to the nearest tenth, approximately how many kilometers is 4,170,000 inches?
A.
10.6 kilometers
B.
16.4 kilometers
C.
106 kilometers
D.
164.2 kilometers
Answers
Answer:
A-10.6 Kilometers
Step-by-step explanation:
1 kilometer =39370.079 inches
are points a c d and j coplanar
Answers
A rain gutter is made from sheets of
aluminum that are 24 inches wide by
turning up the edges to form right
angles. Determine the depth of the
gutter that will maximize its cross-
sectional area and allow the greatest
amount of water to flow. What is the
maximum cross-sectional area?
Flat sheet 24 inches wide
1 Write a quadratic function for the Area in terms of x: A(x) =
2 The cross-sectional area is maximized when the depth of the gutter is
3 The maximum cross-sectional area is square inches.
Answers
1. The quadratic function for the Area in terms of x: A(x) = 24x.
2. The cross-sectional area is maximized when the depth of the gutter is 0.
3. The maximum cross-sectional area is square inches 0.
To determine the depth of the gutter that maximizes its cross-sectional area and allows the greatest amount of water to flow, we need to follow a step-by-step process.
1. Write a quadratic function for the area in terms of x:
The cross-sectional area of the gutter can be represented as a rectangle with a width of 24 inches and a depth of x. Therefore, the area, A(x), is given by A(x) = 24x.
2. The cross-sectional area is maximized when the depth of the gutter is:
To find the value of x that maximizes the area, we need to find the vertex of the quadratic function. The vertex of a quadratic function in form f(x) = ax² + bx + c is given by x = -b/(2a). In our case, a = 0 (since there is no x² term), b = 24, and c = 0. Thus, the depth of the gutter that maximizes the area is x = -24/(2 * 0) = 0.
3. The maximum cross-sectional area is square inches:
Substituting the value of x = 0 into the quadratic function A(x) = 24x, we get A(0) = 24 * 0 = 0. Therefore, the maximum cross-sectional area is 0 square inches.
Know more about the quadratic function here:
https://brainly.com/question/1214333
#SPJ8