Two species of birds are being compared. Species A can fly 18.9 miles in 42 minutes, while species B can fly 20.3 miles in 58 minutes. Which species is slower, and at what speed can it fly?
Answers
Answer:
all i know is species A is faster, but i dont really feel like seeing witch one goes how much slower or faster
Step-by-step explanation:
ok so if you use the unit speed, you should get a higher one for species A.
Related Questions
In t years, the population of a certain city grows from 400,000 to a size P given by P() = 400,000 + 70001? dP a) Find the growth rate, dt b) Find the population after 15 yr. c) Find the growth rate at t=15. d) Explain the meaning of the answer to part (c).
Answers
The growth rate of the population is given by 14,000t, the population after 15 years is 1,975,000, the growth rate at t = 15 is 210,000, and it represents the rate at which the population is increasing at that specific point in time.
To find the growth rate of the population, we need to take the derivative of the population function P(t) with respect to t, which represents the rate at which the population is changing over time.
a) dP/dt = d/dt (400,000 + 7000t²)
= 0 + 2(7000)t
= 14,000t
The growth rate of the population is given by the derivative dP/dt, which is 14,000t.
b) To find the population after 15 years, we substitute t = 15 into the population function P(t).
P(15) = 400,000 + 7000(15)²
= 400,000 + 7000(225)
= 400,000 + 1,575,000
= 1,975,000
The population after 15 years is 1,975,000.
c) To find the growth rate at t = 15, we substitute t = 15 into the derivative dP/dt.
dP/dt (15) = 14,000(15)
= 210,000
The growth rate at t = 15 is 210,000.
d) The meaning of the growth rate at t = 15 (210,000) is that at that specific point in time, the population is growing at a rate of 210,000 individuals per year. This indicates how fast the population is increasing at that particular time.
Therefore, The growth rate of the population is given by 14,000t, the population after 15 years is 1,975,000, the growth rate at t = 15 is 210,000, and it represents the rate at which the population is increasing at that specific point in time.
To know more about growth rate check the below link:
https://brainly.com/question/25849702
#SPJ4
Which quadratic equation has root -6 and 5?
x^2+6x-5=0
x^2+5x-6=0
x^2-x+30=0
x^2+x-30=0
Answers
See attachment for answer and math work.

a car starts off 163 miles directly north from the city of johnstown. it travels due east at a speed of 33 miles per hour. after travelling 63 miles, how fast is the distance between the car and johnstown changing? (do not include units in your answer, and round to the nearest hundredth.)
Answers
The distance between the car and Johnstown is decreasing at a rate of 33 miles per hour.
After travelling 63 miles, the distance between the car and Johnstown is changing at a rate of 33 miles per hour, and the distance between the car and Johnstown is 100 miles
To calculate the distance between the car and Johnstown after travelling 63 miles, we need to first find the starting distance.
The car starts off 163 miles directly north from the city of Johnstown, so the starting distance is 163 miles.
We then need to subtract the distance travelled from this starting distance. Since the car is travelling at a rate of 33 miles per hour, it has travelled 63 miles in the given time.
Therefore, the distance between the car and Johnstown is 100 miles
(163 - 63 = 100).
Finally, we need to calculate the rate of change of this distance. Since the car is travelling at a rate of 33 miles per hour, the rate of change of the distance between the car and Johnstown is also 33 miles per hour.
Learn more about the speed:
https://brainly.com/question/27888149
#SPJ4
. True or false. Randomization distributions are centered at the value where the null is true. True False
Answers
False. Randomization distributions are centered at the value where the null is false. This distinction is important in hypothesis testing as it helps determine the statistical significance of observed differences or effects.
Randomization distributions are generated through permutation tests, which involve random shuffling of data points between groups. In hypothesis testing, the null hypothesis assumes that there is no difference between groups or no effect of a treatment. The alternative hypothesis suggests otherwise.
The randomization distribution is created by repeatedly shuffling the data and calculating a test statistic based on the null hypothesis. This distribution represents the expected outcomes if the null hypothesis is true. Therefore, the randomization distributions are centered at the value where the null is false, as they capture the potential differences or effects between groups.
In summary, randomization distributions are not centered at the value where the null is true; rather, they are centered at the value where the null is false. This distinction is important in hypothesis testing as it helps determine the statistical significance of observed differences or effects.
To know more about hypothesis visit:
https://brainly.com/question/32562440
#SPJ11
Ronnie has an after school job at an animal shelter. She notices that at one meal, 3 cats will eat 2 cans of food.
(a) How much food can 1 cat eat?
(b) Write a formula that Ronnie can use to determine how many cans of food to use per meal based on the number of cats in the shelter.
(c) If there are 12 cats in the shelter, how many cans of food per meal should ronnie food the cats?
Answers
a. The quantity of food that 1 cat can eat is 0.67 (2/3) of a can per meal.
b) A suitable formula that Ronnie can use to determine the cans of food to use per meal is = 0.67x (0.67 X x) where x = number of cats.
c) With 12 cats, the number of cans of food per meal that Ronnie should feed the cats = 8 cans (0.67 x 12).
Thus, a cat can only eat about 67% of a can per meal and 12 cats can eat 8 cans per meal.
Link to related question on multiplication at https://brainly.com/question/12353086
A straight line PQ cuts the x andy axis at M and N respectively. If the points A(-3,5) and B(4,7) lies on PQ , calculate
1.the coordinate of M and N
2./AB/, correct to one decimal place
3.The eqation PQ
I need answers urgently.
pls
Answers
find the volume of a cylinder if the radius is 8cm and the height is 15cm?
Answers
Answer:
3015.92894745 cm^3
Step-by-step explanation:
Formula for volume of cylinder(v)= πr^2h
Here,
r=8 cm
h=15cm
Now,
V=πr^2h=π8^2*15=π64*15=960π=3015.92894745 cm^3
\(2\pir = 1828 + 49 = \)Hey Shona playing how much town
Which algebraic expression is a polynomial with a degree of 4?

Answers
Answer:
for ponits
Step-by-step explanation:
What is the radius of the circle if it has a circumference of 153.86153.86153, point, 86 units.
Answers
Answer:
24.49 units
Step-by-step explanation:
The circumference of the circle is 153.86 units.
The circumference of a circle is given as:
C = 2 * pi * r
where r = radius of the circle
Therefore:
r = C / (2 * pi)
=> r = 153.86 / (2* pi) = 24.49 units
The radius of the circle is 24.49 units.
Answer:
24.49
Step-by-step explanation:
please trust me and make me brainliest :0
Simplify fully 8x/12x2y
Answers
Answer:
2/3xy.
Step-by-step explanation:
8x/12x^2y
The 8 and 12 simplify to 2/3 and x and x^2 simplify to 1/x so we have:
= 2/3xy.
in the fire academy, we had a ratio of 7 to 5 passing grades to failing. how many of the 36 students failed?
Answers
In the fire academy, with a ratio of 7 passing grades to 5 failing grades, we find that approximately 15 students failed.
Given the ratio of 7 passing grades to 5 failing grades, we can set up a proportion to determine the number of students who failed out of 36 students.
Let's denote the number of students who failed as x.
The proportion can be set up as follows:
7 passing grades / 5 failing grades = 36 total students / x failed students
Cross-multiplying the proportion, we have:
7x = 5 * 36
Simplifying the equation, we get:
7x = 180
Dividing both sides of the equation by 7, we find:
x = 180 / 7
Calculating the value, we have:
x ≈ 25.71
Since we cannot have fractional students, we round down to the nearest whole number.
Therefore, approximately 25 students failed out of the 36 students in the fire academy.
Learn more about ratio here:
https://brainly.com/question/26974513
#SPJ11
Find the slope through the given points Show your work. (2, 3) and (-5, 4)
Answers
x1-y1 and x2-y2 gives you 2-(-5) and 3-4, so you now have a point which is (7,-1) which is the slope.
A two-variable inequality is shown in the graph.
upward opening parabola which is dashed with vertex at 1 comma 2, travels through points negative 1 comma 6 and 3 comma 6, with shading outside the curve.
Which point is not included in the solution set for the inequality?
(–2, 1)
(1, 3)
(4, 3)
(5, –1)

Answers
Answer: (1,3)
Step-by-step explanation: All you're doing with this outward-shaded parabola is just seeing which points are in the red and which points are not. The point that isn't in the red is the point not included in the solution set. If you plot all the points given, you'll see that (1,3) is in the white. :)
The point (-2, 1) is not included in the solution set.
Explanation:The given inequality describes an upward opening parabola with a dashed line. The vertex of the parabola is (1, 2), and it passes through the points (-1, 6) and (3, 6). The shading outside the curve represents the solution set for the inequality.
To determine which point is not included in the solution set, we can test each point in the inequality. Let's start with (-2, 1).
Plugging in the x- and y-coordinates of (-2, 1) into the inequality, we get: 1 < (2 - 1)^2. Simplifying this inequality, we have 1 < 1, which is false. Therefore, (-2, 1) is NOT included in the solution set.
Now, let's test the remaining points: (1, 3), (4, 3), and (5, -1). By substituting these points into the inequality, we can determine whether they satisfy the inequality or not.
Based on our calculations, the point that is not included in the solution set for the inequality is (-2, 1).
Learn more about Inequality and parabola here:https://brainly.com/question/31992012
#SPJ2
5a) Determine the measure of each unknown angle

Answers
Answer:
Step-by-step explanation:
25, i think
Aiko is finding the sum (4 5i) (–3 7i). She rewrites the sum as (–3 7)i (4 5)i. Which statement explains the error Aiko made by using a mathematical property incorrectly?.
Answers
Answer:
Distribute Property
Step-by-step explanation:
In the first expression, 7 is the only coefficient of i in the second term, and 5 is the only coefficient of i in the first term. The rewritten sum would simplify to -3i +7i +4i+5i.
Use the inner product (p, q) = a b + a₁b₁ + a₂b₂ to find (p, q), ||p|, ||a||, and d(p, q) for the polynomials in P₂. p(x) = 1 − x + 4x², g(x) = x - x² (a) (p, q) (b) ||p|| (c) ||a|| (d) d(p, q) Find (u, v), u, v, and d(u, v) for the given inner product defined on R". u = (0, 2, 3), v = (2, 3, 0), (u, v) = u · v (a) (u, v) (b) ||ul| (c) ||v|| (d) d(u, v)
Answers
For the polynomials p(x) = 1 - x + 4x² and q(x) = x - x², (p, q) = 10, ||p|| = √18, ||a|| = √18, and d(p, q) cannot be determined. For the vectors u = (0, 2, 3) and v = (2, 3, 0), (u, v) = 6, ||u|| = √13, ||v|| = √13, and d(u, v) cannot be determined.
In the first scenario, we have p(x) = 1 - x + 4x² and q(x) = x - x². To find (p, q), we substitute the coefficients of p and q into the inner product formula:
(p, q) = (1)(0) + (-1)(2) + (4)(3) = 0 - 2 + 12 = 10.
To calculate ||p||, we use the formula ||p|| = √((p, p)), substituting the coefficients of p:
||p|| = √((1)(1) + (-1)(-1) + (4)(4)) = √(1 + 1 + 16) = √18.
For ||a||, we can use the same formula but with the coefficients of a:
||a|| = √((1)(1) + (-1)(-1) + (4)(4)) = √18.
Lastly, d(p, q) represents the distance between p and q, which can be calculated as d(p, q) = ||p - q||. However, the formula for this distance is not provided, so it cannot be determined. Moving on to the second scenario, we have u = (0, 2, 3) and v = (2, 3, 0). To find (u, v), we use the given inner product formula:
(u, v) = (0)(2) + (2)(3) + (3)(0) = 0 + 6 + 0 = 6.
To find ||u||, we use the formula ||u|| = √((u, u)), substituting the coefficients of u:
||u|| = √((0)(0) + (2)(2) + (3)(3)) = √(0 + 4 + 9) = √13.
Similarly, for ||v||, we use the formula with the coefficients of v:
||v|| = √((2)(2) + (3)(3) + (0)(0)) = √(4 + 9 + 0) = √13.
Unfortunately, the formula for d(u, v) is not provided, so we cannot determine the distance between u and v.
Learn more about distance here: https://brainly.com/question/29130992
#SPJ11
Jasjeet and her brother collect stamps.
When Jasjeet gives her brother 1% of her stamps, she has 2475 stamps left.
Calculate how many stamps Jasjeet had originally.
Answers
Answer:
2500
Step-by-step explanation:
If Jasjeet gave away 1%, that means she has 99% left.
Put the 99% over 100, so you can drop the % sign.
Then you're going to cross multiply that with 2475/ ?. The ? is the unknown aka original ammount of stamps. The 2475 is the 99% of stamps she still has.
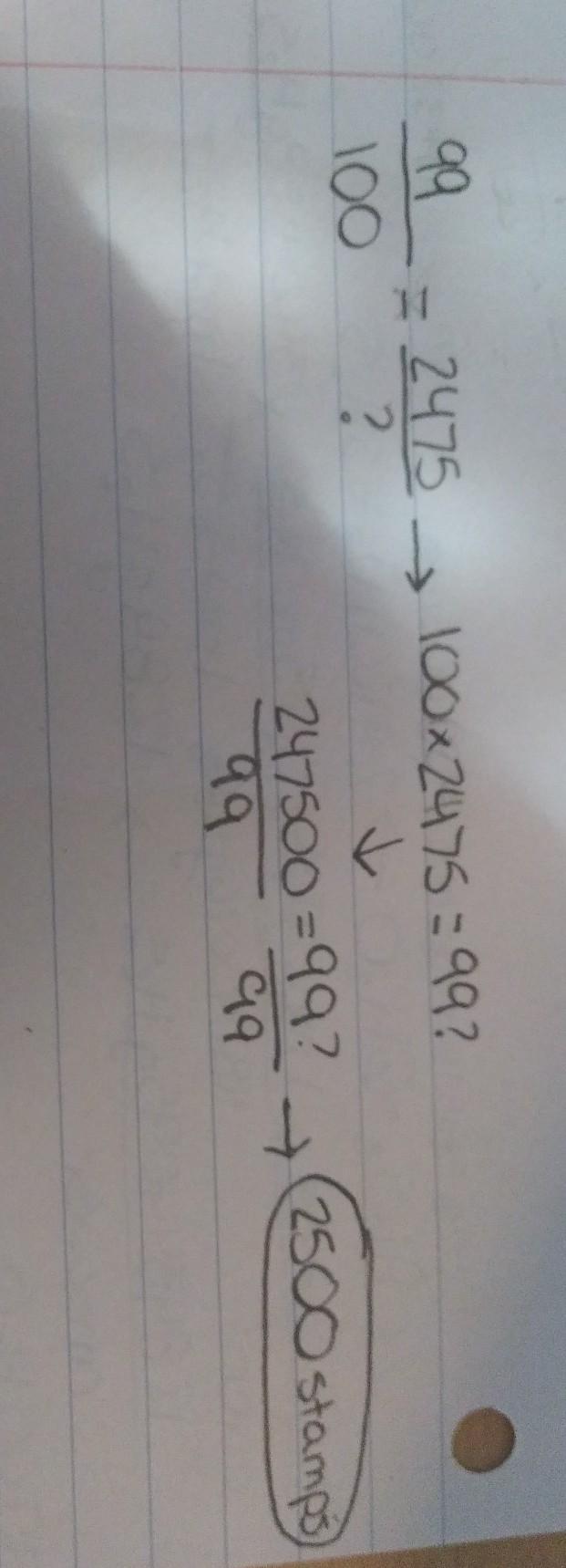
A person invested \$790$790 in an account growing at a rate allowing the money to double every 13 years. How much money would be in the account after 30 years, to the nearest dollar?
Answers
Answer:3911
Step-by-step explanation:
Saw the answer
Answer:
Step-by-step explanation:
3911
Quadrilateral ABCD will be dilated about the origin by a scale factor of and then reflected across they-axis.А987654DB321-6-5-2-8-4-1702B5-1-2-30C-4-5-6-7Identify the coordinates of the points after the transformation:Byes

Answers
SOLUTION:
Step 1:
In this question, we have that the Quadrilateral ABCD will be dilated about the origin by a scale factor of 1/3 and then reflected across the y-axis:
From the graph, we can see that:
\(\begin{gathered} A(\text{ -3, 9 )} \\ B(\text{ -6, 3 )} \\ C(0,\text{ -3)} \\ D(3,\text{ 3)} \end{gathered}\)Step 2:
We need to dilate about the origin by a scale factor of 1/3, then
we have that:
\(\begin{gathered} A\text{ ( - 1 , 3 )} \\ B\text{ ( - 2, 1)} \\ C\text{ ( 0, -1)} \\ D(\text{ 1, 1 )} \end{gathered}\)Step 3 :
We need to reflect across the y-axis:
( x , y ) ------- ( -x, y )
\(\begin{gathered} A(-1,3)------A^{I\text{ }}(\text{ 1, 3 )} \\ B(-2,1)------B^I\text{ ( 2, 1)} \\ C(0,-1)------C^I\text{ ( 0, -1)} \\ D(1,1)-------D^I\text{ ( -1 , 1 )} \end{gathered}\)From the graph,
a) The original polygon is in colour Red
b) The dilated image of the original polygon is in colour Blue
c) The reflection of the dilated image is in colour Green.

find the mean and median and made of the following data 30,31,35,29,32,30,31,35,36,35
Answers
median- 31.5
mode- 35
Answer:
mean- 32.4
median- 31.5
mode- 35
Step-by-step explanation:
to find mean add up all the number together than divide it by how many number that are there
for example the total is 324 and you would divide it by 10 (since there are 10 number there)
to find median locate the middle number but since you have two number in the middle take those to number add them together and divide by 2
for example 31+32=63 than divide by 2 which is 31.5
to find mode it is the number that appears most often so it would be 35 since it appears most often
Let K = {,:ne Z+} be a subset of R. Let B be the collection of open intervals (a,b) along with all sets of the form (a,b) K. Show that the topology on R generated by B is finer than the standard topology on R.
Answers
Each Bj is an open interval or a set of the form (a,b) ∩ K, each Bj is open in the topology generated by B. Hence, U is a union of open sets in the topology generated by B and the topology generated by B is finer than the standard topology.
Given that K = {x : x is not a positive integer}. Also, B is the collection of open intervals (a,b) along with all sets of the form (a,b) ∩ K. We need to prove that the topology on R generated by B is finer than the standard topology on R.
Let's start with the following lemma:
Lemma: Every open interval in the standard topology is a union of elements of B.
Proof: Let (a,b) be an open interval in the standard topology. If (a,b) ∩ K = ∅, then (a,b) ∈ B and we are done. Otherwise, we can write(a,b) = (a,c) ∪ (c,b)where c is the smallest positive integer such that c > a and c < b.
Now, (a,c) ∩ K and (c,b) ∩ K are both in B. Therefore, (a,b) is a union of elements of B.
Now, let's prove that B generates a finer topology on R than the standard topology.
Let U be an open set in the standard topology and x be a point in U. Then there exists an open interval (a,b) containing x such that (a,b) ⊆ U. By the above lemma, we can write (a,b) as a union of elements of B.
Therefore, there exist elements B1, B2, ..., Bn of B such that (a,b) = B1 ∪ B2 ∪ ... ∪ Bn.
Since each Bj is an open interval or a set of the form (a,b) ∩ K, each Bj is open in the topology generated by B. Therefore, (a,b) is a union of open sets in the topology generated by B.
Hence, U is a union of open sets in the topology generated by B. Therefore, the topology generated by B is finer than the standard topology.
To know more about topology, visit the link : https://brainly.com/question/30224057
#SPJ11
please help its timed thank u

Answers
Answer:the third one (c)
Step-by-step explanation:
What is 4^4 in algerbra mathematics?
Answers
Answer:
256
Step-by-step explanation:
4 to the exponent of 4 = 256
A hurricane wiped out 40% of the wild rats in a coastal city. Then, a disease spread through stagnant water killing 20% of the rats that survived the hurricane. What percentage of the original population of rats is left after these 2 events
Answers
After the hurricane and the disease, 48% of the original population of rats is left.
We have,
After the hurricane, 40% of the rats were wiped out, which means
100% - 40% = 60% of the rats survived.
Then, after the disease spread through stagnant water, 20% of the remaining rats were killed.
This means 100% - 20% = 80% of the rats that survived the hurricane are still left.
To find the percentage of the original population of rats that is left after both events, we multiply the percentages:
Percentage left = 60% * 80% = 0.6 * 0.8 = 0.48
Finally, we convert the decimal value back to a percentage:
Percentage left = 0.48 * 100% = 48%
Therefore,
After the hurricane and the disease, 48% of the original population of rats is left.
Learn more about percentages here:
https://brainly.com/question/11403063
#SPJ4
help
un productor de cafe ha vendido 250 kg a 18 cada uno.si sus costos de produccion ascienden los 2800,cual ha sido su ganancia?
Answers
Answer:
ganancia $1700
Step-by-step explanation:
250X18 = 4500 (ventas)
costo 2800
ganancias = ventas-costo
4500-2800 = 1700
soh cah toa...does anyone know this?

Answers
Answer:
SOH: Sin(θ) = Opposite / Hypotenuse
CAH: Cos(θ) = Adjacent / Hypotenuse
TOA: Tan(θ) = Opposite / Adjacent
Step-by-step explanation:
So how do we remember these three trig ratios and use them to solve for missing sides and angles?
First, we remember how the sides of a right triangle are labeled:
Opposite Leg
Adjacent Leg
Hypotenuse
The opposite leg is opposite one of the acute angles, the adjacent leg is next to the acute angle, and the hypotenuse is opposite the right angle, or as Math is Fun nicely states, it’s the long one.
opposite adjacent hypotenuse diagram
Right Triangle Diagram
Then we use the mnemonic device we talk about earlier: SOHCAHTOA!
So how do we remember these three trig ratios and use them to solve for missing sides and angles?
First, we remember how the sides of a right triangle are labeled:
Opposite Leg
Adjacent Leg
Hypotenuse
The opposite leg is opposite one of the acute angles, the adjacent leg is next to the acute angle, and the hypotenuse is opposite the right angle, or as Math is Fun nicely states, it’s the long one.
opposite adjacent hypotenuse diagram
Right Triangle Diagram
Then we use the mnemonic device we talk about earlier: SOHCAHTOA!
∠VTW≅∠UTW and ∠U≅∠V. Complete the proof that
VW
≅
UW
.
T
U
V
W
Answers
Answer: did you make that up ??
Step-by-step explanation:
Answer:
A. Alternate interior
B. Transitive property
C. Converse alternate interior angles theorem.
At Lara' party, 4 gallon of fruit punch are hared equally among 18 friend. How much fruit punch will each peron get?
Answers
Answer: About 0.2 gallons
Step-by-step explanation: 4/18=0.2 repeating, so each person gets about 0.2 gallons.
Each of her friend will get 4 and a half gallons of juice.
What is division?Division is one of the four main arithmetical operations by which we find the equal distribution of something.
Given that, At Lara's party, 4 gallon of fruit punch are shared equally among 18 friend.
To find how much each of them got, we will divide total amount of punch by total number friends
Amount of juice each of them gets, = 18/4 = 4.5
Hence, Each of her friend will get 4 and a half gallons of juice.
For more references on divisions, click;
https://brainly.com/question/21416852
#SPJ2
.
Charles Brady King drove the first automobile in Detroit
on March 6 of this year. Solve the puzzle to learn the
* Srous year!!!
My units digit is the same as the number of lines of
symmetry in a regular hexagon.
The two-digit number formed by my hundreds and
tens digits is equal to the suppliment of a 91° angle.
The sum of all my digits is the number whose prime
factorization is 23 X 3.
What year am I?_
Answers
Based on the illustration, the year we are looking for is 1769.
Charles Brady King drove the first automobile in Detroit on March 6 of 1896.
To solve the puzzle, we need to find a two-digit number whose units digit is the same as the number of lines of symmetry in a regular hexagon, which is six.
The hundreds and tens digits must add up to the supplement of a 91° angle, which is 89°, giving us the number 98.
The sum of all the digits in 98 is 9+8=17, and the prime factorization of 23x3 is 69.
Learn more about mathematical model at
https://brainly.com/question/731147
#SPJ11
What equivalent to 6/1