Un padre está usando una manguera de jardín para llenar una pequeña piscina inflable para su hijo pequeño. La piscina tiene una capacidad de 90 galones. Apaga el agua después de 5 minutos, pero deja la manguera en la piscina durante otros 3 minutos antes de guardarla. En esta situación, la relación entre los galones de agua en la piscina y los 8 minutos desde que el padre comenzó a llenar la piscina puede verse como una función. 1. En esa función, ¿qué variable es independiente? ¿Cuál es dependiente?
Answers
Answer:
Water is being collected at the rate of 11.25 gallon per minute.
Step-by-step explanation:
In this function the filling of water in the pool is dependent on the number of minutes. The more time the tap is opened the greater amount of water can be accumulated in the pool .
So time is independent and water is the dependent variable.
The function can be represented by
f(x)= xt where t is the time in minutes
90 gallons= x * 8 minutes
or x= 90/8 = 11.25 gallon per minute.
So water is being collected at the rate of 11.25 gallon per minute.
Spanish
En esta función, el llenado de agua de la piscina depende de la cantidad de minutos. Cuanto más tiempo se abre el grifo, mayor cantidad de agua se puede acumular en la piscina.
Entonces el tiempo es independiente y el agua es la variable dependiente.
La función se puede representar por
F (x) = xt donde t es el tiempo en minutos
90 galones = x * 8 minutos
o x = 90/8 = 11,25 galones por minuto.
Entonces, el agua se recolecta a una velocidad de 11.25 galones por minuto.
Related Questions
Find an antiderivative F(x) with F′(x)=f(x)=4+15x2+15x4 and F(1)=0.
Remember to include a "+ C" if appropriate.
F(x)=
Answers
The antiderivative of the function is F(x) = 4x + 5x^3 + 3x^5 - 12.
To find the antiderivative F(x) for F′(x) = f(x) = 4 + 15x^2 + 15x^4, and given F(1) = 0, follow these steps,
1. Find the antiderivative of f(x) with respect to x:
F(x) = ∫(4 + 15x^2 + 15x^4) dx
2. Integrate each term separately:
F(x) = ∫4 dx + ∫15x^2 dx + ∫15x^4 dx
3. Calculate the antiderivatives:
F(x) = 4x + (15/3)x^3 + (15/5)x^5 + C
4. Simplify:
F(x) = 4x + 5x^3 + 3x^5 + C
5. Use the given condition F(1) = 0 to find the value of C:
0 = 4(1) + 5(1)^3 + 3(1)^5 + C
6. Solve for C:
C = -12
7. Substitute the value of C back into F(x):
F(x) = 4x + 5x^3 + 3x^5 - 12
The antiderivative is F(x) = 4x + 5x + 3x - 12 as a result.
Learn more about "antiderivative": https://brainly.com/question/12956882
#SPJ11
The population, in millions, of arctic flounder in the Atlantic Ocean is modeled by the function P(t), where t is measured in ye 7t + 5 P(t) 0.2t2 + 1 (a) Determine the initial flounder population (in millions). million flounder (b) Determine P'(10) (in millions of flounder per year). (Round your answer to four decimal places.) P'(10) - million flounder/yr
Answers
The initial flounder population in millions is 1 million. The derivative of the population function at t = 10 is 1.4000 million flounder per year.
(a) To find the initial flounder population, we substitute t = 0 into the population function P(t). Given that t is measured in years, we have:
P(0) = 7(0) + 5 - 0.2(0^2) + 1 = 0 + 5 - 0 + 1 = 6 million flounder.
Therefore, the initial flounder population is 6 million.
(b) To determine P'(10), we need to find the derivative of the population function P(t) and evaluate it at t = 10. Taking the derivative of P(t) with respect to t, we have:
P'(t) = 7 + 0.4t.
Now, substituting t = 10 into the derivative equation:
P'(10) = 7 + 0.4(10) = 7 + 4 = 11 million flounder per year.
Rounded to four decimal places, P'(10) is approximately 11.0000 million flounder per year.
Learn more about decimal here:
https://brainly.com/question/30958821
#SPJ11
What is the equation of a line that is perpendicular perpendicular to y=-(3)/(4)x+9 and goes through the point (6,4)
Answers
The equation of a line that is perpendicular to y=-(3)/(4)x+9 and goes through the point (6,4) is y = 4x/3 - 14/3.
Given line is y = -(3)/(4)x+9
We know that if two lines are perpendicular to each other, the product of their slopes is equal to -1.Let the required equation of the line be y = mx+c.
Therefore, the slope of the line is m.To find the slope of the given line:y = -(3)/(4)x+9
Comparing it with the general equation of a line:y = mx+c
We can say that slope of the given line is -(3/4).
Therefore, slope of the line perpendicular to the given line is: -(1/(-(3/4))) = 4/3
Let the equation of the perpendicular line be y = 4/3x+c.
The line passes through (6, 4).Therefore, we have:4 = 4/3 * 6 + c4
= 8 + cC
= 4 - 8
= -4
Therefore, the equation of the required line is:y = 4x/3 - 14/3.
To know more about perpendicular visit:
https://brainly.com/question/12746252
#SPJ11
Determine if a triangle can be formed with given length if yes classify as acute right or obtuse

Answers
1) cos α = 0.8, cos β = 0.6, cos γ = 0. The triangle exists and is right.
2) cos α ≈ 0.882, cos β ≈ 0.471, cos γ ≈ 0.441. The triangle exists and is acute.
3) cos α ≈ 0.977, cos β ≈ 0.324, cos γ ≈ -0.115. The triangle exists and is obtuse.
4) cos α = 1, cos β = 1, cos γ = -1. The triangle does not exist.
How to determine if a triangle may exist and the existence of given angles
Triangles are geometric figures formed by three line segments and internal angles, whose sum is equal to 180°, which can be three acute angles or an obtuse angle and two acute angles or a right angle and two acute angles. The possibility is determined by applying the law of cosine:
\(\cos \theta = -\frac{x^{2}-y^{2}-z^{2}}{2\cdot y\cdot z}\) (1)
The triangle if and only if the cosine of each angle is between -1 and 1 with the following characteristics:
If the cosine of the angle is between 0 and 1, then it is acute.If the cosine of the angle is 0, then it is right.If the cosine of the angle is between 0 and -1, then it is obtuse.Now we proceed to determine the existence of each triangle:
1) cos α = 0.8, cos β = 0.6, cos γ = 0. The triangle exists and is right.
2) cos α ≈ 0.882, cos β ≈ 0.471, cos γ ≈ 0.441. The triangle exists and is acute.
3) cos α ≈ 0.977, cos β ≈ 0.324, cos γ ≈ -0.115. The triangle exists and is obtuse.
4) cos α = 1, cos β = 1, cos γ = -1. The triangle does not exist.
To learn more on triangles, we kindly invite to check this: https://brainly.com/question/2773823 #SPJ1
estimate the change in the advertising budget necessary to maintain a monthly profit of $93,500 if the insurance company hires 5 new sales associates.
Answers
The change in the advertising budget necessary to maintain a monthly profit of $93,500 if the insurance company hires 5 new sales associates is estimated to be an increase of $2,308.
To estimate the change in advertising budget necessary to maintain a monthly profit of $93,500 with the addition of 5 new sales associates, we need to consider the potential impact of these new hires on the company's revenue and expenses.
Assuming that each new sales associate is expected to generate $10,000 in revenue per month, the total increase in revenue would be $50,000 (5 sales associates x $10,000).
However, there may also be additional expenses associated with the new hires, such as salaries and benefits. Let's assume that the total cost of adding 5 new sales associates is $30,000 per month.
Therefore, the net increase in monthly profit due to the new hires would be $20,000 ($50,000 in revenue - $30,000 in expenses).
To maintain a monthly profit of $93,500, the company would need to increase its advertising budget by an amount that would generate an additional $20,000 in profit. Assuming that the company's profit margin on its products is 20%, this would require an additional $100,000 in revenue per month ($20,000 / 0.20).
Based on the historical data and market conditions, the company could estimate the additional advertising budget required to generate this amount of revenue.
To know more about revenue refer here:
https://brainly.com/question/31683012
#SPJ11
The residents of city voted.
on whether to raise property
taxes. The ratio of yes votes
to no votes was 5 to 4. If
there were 6741 total votes,
how many no
votes were there?
Answers
Answer:
2996
Step-by-step explanation:
5x + 4x = 6741
9x = 6741
x = 6741/9
x = 749
to get the no votes,
4x i.e 4*749
=> 4*749 = 2996
hope this helps :)
Answer:
2996
Step-by-step explanation:
The result from ANDing 11001111 with 10010001 is ____. A) 11001111
B) 00000001
C) 10000001
D) 10010001
Answers
The result of ANDing 11001111 with 10010001 is 10000001. Option C
To find the result from ANDing (bitwise AND operation) the binary numbers 11001111 and 10010001, we compare each corresponding bit of the two numbers and apply the AND operation.
The AND operation returns a 1 if both bits are 1; otherwise, it returns 0. Let's perform the operation:
11001111
AND 10010001
10000001
By comparing each corresponding bit, we can see that:
The leftmost bit of both numbers is 1, so the result is 1.
The second leftmost bit of both numbers is 1, so the result is 1.
The third leftmost bit of the first number is 0, and the third leftmost bit of the second number is 0, so the result is 0.
The fourth leftmost bit of the first number is 0, and the fourth leftmost bit of the second number is 1, so the result is 0.
The fifth leftmost bit of both numbers is 0, so the result is 0.
The sixth leftmost bit of both numbers is 1, so the result is 1.
The seventh leftmost bit of both numbers is 1, so the result is 1.
The rightmost bit of both numbers is 1, so the result is 1.
Option C
For more such question on ANDing visit:
https://brainly.com/question/4844870
#SPJ8
Use series to evaluate the limit. Lim x→0 1 3 x3 − 1 2 x2 x − ln(1 x) x4
Answers
By using Taylor series, the limit does not exist, since the third term does not converge as x approaches 0.
To evaluate the limit using series, we can use the Taylor series expansion of each term in the limit as x approaches 0. A Taylor series is an infinite sum of terms that are expressed in terms of the derivatives of a function at a single point.
Starting with the first term:
lim x→0 (1/3) * x^3 = 0
Next, for the second term, we have:
lim x→0 ((x^3 - 1)/(2x^2)) = lim x→0 (x^3/2x^2) = lim x→0 (x/2) = 0
For the third term, we have:
lim x→0 (x - ln(1 + x))/x^4
= lim x→0 [(x - (x - x^2/2 + x^3/3 - ...))/x^4] (using the Taylor series expansion of ln(1+x))
= lim x→0 [x^2/2 - x^3/3 + ...]/x^4
= lim x→0 [1/2x^2 - 1/3x^3 + ...]
= ∞
Therefore, the limit does not exist, since the third term does not converge as x approaches 0.
To know more about Taylor series:
https://brainly.com/question/29733106
#SPJ4
8. The equivalent of ¾ inch is __________?

Answers
Answer: 0.75
Step-by-step explanation:
in a normal distribution, about how much of the distribution lies within two (2) standard deviations of the mean?a. 95%b. 90%c. 80%
Answers
Answer: a. 95%
In a normal distribution, about 95% of the distribution lies within two standard deviations of the mean.
Help please I will give you the brainliest

Answers
Answer:
its the first one and here is some advice go to the website m a t h w a y and enter the equation and click graph!
Step-by-step explanation:
The expressions (-3) to the 2nd power and -3 to the second power have the same value, true or false justify your answer?
Answers
The statement 'the expressions (-3) to the 2nd power and -3 to the second power have the same value' is True.
For given question,
We have been given a statement '(-3) to the 2nd power'
This statement can be written in expression form as,
(-3)²
Now we find the value of above expression.
(-3)² = (-3) × (-3)
= 9 .................(1)
Also, we have been given a statement '-3 to the second power'
This statement can be written in expression form as,
(-3)²
Now we find the value of above expression.
(-3)² = (-3) × (-3)
= 9 .................(2)
From (1) and (2),
We can say that the value of expressions '(-3) to the 2nd power' and '-3 to the second power' is same.
Therefore, the statement 'the expressions (-3) to the 2nd power and -3 to the second power have the same value' is True.
Learn more about an expression here:
https://brainly.com/question/14083225
#SPJ4
STT 1.3 Sarah starts at a positive position along the x-axis. She then undergoes a negative displacement. Her final position
A is postive
B Is negative
C Could be either positive or negative
Answers
Sarah's final position would be negative. Therefore, option B is the correct answer.
Given that, Sarah starts at a positive position along the x-axis. She then undergoes a negative displacement.
A negative displacement means that Sarah has moved backward along the x-axis, so her final position would be negative.
Therefore, option B is the correct answer.
To learn more about an integers visit:
https://brainly.com/question/15276410.
#SPJ4
if I have 2/5 times 9/5 I don't know
Answers
Answer:
18/25
Step-by-step explanation:
If this answer helped you then please mark it as brainliest so I can get to the next rank
Answer:18/25
Step-by-step explanation:
2. 9. 2x9. = 18
- X. - = ————- It cannot be simplified
5. 5. 5x5=25
Use substitution to write an equivalent quadratic equation. (3x 2)2 7(3x 2) â€"" 8 = 0
Answers
Answer: We on da same question i do not know
Step-by-step explanation:
Calculate the line integral of the function v = x2 + 2yzâ + y²g from (0, 0, 0) the point (1, 1, 1) by the route (0,0,0) + (1,0,0) + (1,1,0) + (1,1,1). (10/100)
Answers
To calculate the line integral of the given vector field, we will use the formula of line integral. For the given function, the formula will be:∫CF.v dlWhere v = (x²+2yz)i + y²j and dl = dx i + dy j + dz kTherefore,∫CF.(x²+2yz) dx + y² dy … (1)Here, C is the curve from point (0,0,0) to (1,1,1) along the given route, that is, (0,0,0) + (1,0,0) + (1,1,0) + (1,1,1).∴
The above line integral is the required value. So, we need to evaluate this integral. To calculate the line integral of the given vector field, we will use the formula of line integral. For the given function, the formula will be:
∫CF.v dl
Where
v = (x²+2yz)i + y²j
and
dl = dx i + dy j + dz k
Therefore,
∫CF.(x²+2yz) dx + y² dy … (1)
Here, C is the curve from point (0,0,0) to (1,1,1) along the given route, that is, (0,0,0) + (1,0,0) + (1,1,0) + (1,1,1).∴ The above line integral is the required value. So, we need to evaluate this integral.The integral is a line integral of a vector field, with the curve path of integration is given by C as follows: C: (0,0,0) + (1,0,0) + (1,1,0) + (1,1,1)In other words, we need to evaluate the integral of the dot product of the vector field v with the differential of the curve:
∫CF.v dl...
where
v = (x²+2yz)i + y²j
and
dl = dx i + dy j + dz k
We must split the curve C into three distinct segments before we can start evaluating the integral. The segments will be from (0,0,0) to (1,0,0), from (1,0,0) to (1,1,0), and from (1,1,0) to (1,1,1).Let's start with the first segment, from (0,0,0) to (1,0,0). We can set x = t, y = 0, z = 0, with t varying from 0 to 1, to parametrize this segment. Then dx = dt, dy = 0, dz = 0. We have:∫(0,0,0)to(1,0,0)
vdl = ∫0to1(x²+2yz)dx + y²dy + 0dz= ∫0to1(t²+0)dt + 0 + 0= [t³/3]0to1= 1/3
Now, let's evaluate the second segment, from (1,0,0) to (1,1,0). We can set x = 1, y = t, z = 0, with t varying from 0 to 1, to parametrize this segment. Then dx = 0, dy = dt, dz = 0. We have:
∫(1,0,0)to(1,1,0)vdl = ∫0to1(x²+2yz)dx + y²dy + 0dz= ∫0to1(1²+0)dx + t²dy + 0dz= 1∫0to1(t²)dt= [t³/3]0to1= 1/3
Finally, let's evaluate the third segment, from (1,1,0) to (1,1,1). We can set x = 1, y = 1, z = t, with t varying from 0 to 1, to parametrize this segment. Then dx = 0, dy = 0, dz = dt. We have:
∫(1,1,0)to(1,1,1)vdl = ∫0to1(x²+2yz)dx + y²dy + 0dz= ∫0to1(1²+2(1)(t))dx + 1²dy + 0dz= ∫0to1(1+2t)dt + 1(0to1)+ 0= [t²+t]0to1+ 1= 3/2
Therefore, the line integral is the sum of the integrals along the three segments:
∫CF.v dl= 1/3+ 1/3+ 3/2= 2
Thus, the value of the line integral of the given function v = x²+2yzi + y²j from (0,0,0) the point (1,1,1) by the route (0,0,0) + (1,0,0) + (1,1,0) + (1,1,1) is equal to 2.
To learn more about line integral visit:
brainly.com/question/29850528
#SPJ11
Jasmine had 50 cans and collects 5 additional cans per week for a food drive. Leandra has no cans but collects 10 cans per week. After how many weeks will they have the same number of cans?
Answers
10 weeks
50 cans+additional 5 per week
5×10=50
100
10 per week
10×10=100
The Thornton family is going hiking tomorrow. To get ready, Mrs. Thornton is making trail mix. She mixes 7 cups of nuts, 2 cups of chocolate chips, and 3 cups of raisins. Mrs. Thornton splits the trail mix evenly into 6 bags, one for each family member.
Answers
Answer:
7+2+3=12 pounds in totak
12÷6=2 pounds in each bag
To the nearest tenth of a second, how much longer would it take a dropped penny to fall 100 ft on the Moon than it would on Earth?
s longer
Answers
Answer:
3.6
Step-by-step explanation:
Answer:
3.6
Step-by-step explanation:
Salma and John walk around a track. Salma walks each lap in 10 minutes. John walks each lap in 12 minutes. The two of them begin at the starting line at the
same time. They walk until they meet again at the starting line.
Answers
Answer:
If you're asking how long it will take for them to meet again, it will take 60 minutes.
Step-by-step explanation:
You just won a grand prize that pays you $1000 a month for 9 years. If you can earn 8 percent on your money, what is this prize worth to you today? $100,875.78$122,591.29$64,800.00$14,000.00$76,812.50
Answers
If you can earn 8 percent on your money, the prize worth to you is: $76,812.50. To calculate the present value of the prize, we need to determine the current worth of receiving $1000 per month for 9 years, given an 8 percent annual interest rate.
This situation can be evaluated using the concept of the present value of an annuity. The present value of an annuity formula is used to find the current value of a series of future cash flows. In this case, the future cash flows are the $1000 monthly payments for 9 years. By applying the formula, which involves discounting each cash flow back to its present value using the interest rate, we find that the present value of the prize is $76,812.50.
This means that if you were to receive $1000 per month for 9 years and could earn an 8 percent return on your money, the equivalent present value of that prize, received upfront, would be $76,812.50.
Learn more about discount here: brainly.com/question/31746893
#SPJ11
ANOTHER ONE LOL You exercise for ¾ of an hour. You jump rope ⅓ of that time. What portion of the hour do you spend jumping rope?
Answers
Answer: 15 minutes
Step-by-step explanation:
60 / 4 = 15
15 * 3 = 45
45 / 3 = 15
Answer:
Step-by-step explanation:
Time spent on jump rope = 1/3 of 3/4
\(= \dfrac{1}{3}*\dfrac{3}{4}=\dfrac{1}{4} \ hour\) or 15 minutes
Nick spent 34 minutes on the phone while routing 17 phone calls. In all, how many phone calls does Nick have to route to spend a total of 50 minutes on the phone? Assume the relationship is directly proportional.
Answers
Answer:
25 phone calls
Step-by-step explanation:
Create a proportion where x is the number of phone calls for 50 minutes on the phone:
\(\frac{34}{17}\) = \(\frac{50}{x}\)
Cross multiply and solve for x:
34x = 850
x = 25
So, Nick would have to make 25 phone calls
Evaluate the factorial expression.15!12!(4−1)!
Answers
we have
15!12!(4−1)!
15!12!(3!)=3,758,268,687,305,932,800,000
therefore
the answer is
3,758,268,687,305,932,800,000Look at this graph:
y
100
90
80
70
60
50
40
30
20
10
X
0
10
20 30 40 50 60 70 80 90 100
What is the slope?
Answers
Find the x- and y-intercepts of the graph of each ... CCSS REASONING The equation 5x + 10y = 60 ... 20. SOLUTION: The x-intercept is the point at which the y-coordinate is 0, or the line ... charges $50 for admission before 6 p.m. and $20 for ... (90, 70). 100 f (100) = 160 – (100). 60. (100, 60). 130 f (130) = 160 – (130). 30.
Find the lateral surface area of the figure.
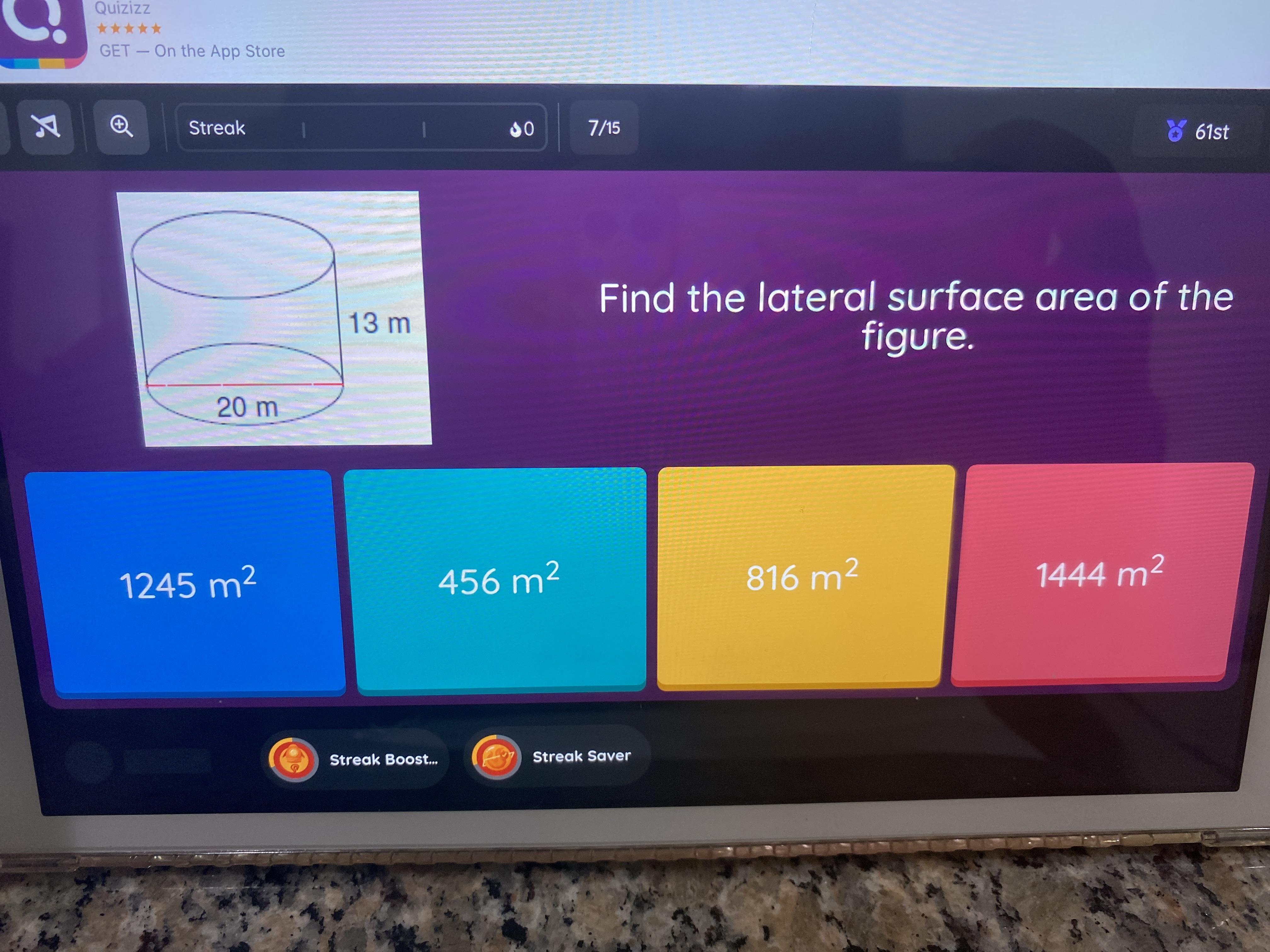
Answers
The evaluated lateral surface area is 261.8 square meters, under the condition that the base length is 20 m and height is 13 m.
The lateral surface area of a cylinder is given by the formula 2πrh
Here,
r = radius of the base
h = height of the cylinder.
For the given case, the base length is 20 m and height is 13 m. Then the base length is stated instead of the radius, we have to evaluate the radius first.
The radius of a cylinder can be found applying the formula r = l/2π
Here,
l = base length.
So, staging l = 20 m
, we get
r = 20/(2π)
≈ 3.18 m
Now that we have received the radius and height, we can evaluate the lateral surface area applying the formula mentioned above.
Staging
r = 3.18 m
h = 13 m,
we get:
Lateral surface area
= 2πrh
≈ 261.8 m²
Then, the lateral surface area of the given cylinder is approximately 261.8 square meters.
To learn more about surface area
https://brainly.com/question/951562
#SPJ1
PLEASE HELP ME ITS DUE TODAY I WILL MARK YOU BRAINLIST
5. Mia is stretching out before dance class. She sometimes places a band around her calves to get an extra stretch.
Part 1: Sketch and label the triangle that illustrates the scenario and givens required for the proof. (3 points)
Part 2: Use the spaces provided below to complete a formal proof. (5 points)


Answers
Answer:
It's Arrives
Step-by-step explanation:
Which products result in a sum or difference of cubes? Check all that apply. (x – 4)(x2 4x – 16) (x – 1)(x2 – x 1) (x – 1)(x2 x 1) (x 1)( x – 1) (x 4)(x2 – 4x 16) (x 4)(x2 4x 16).
Answers
You can open those brackets and distribute one brackets content with multiplication to other bracket contents.
The products which result in a sum or difference of cubes is given by:
Option D: \((x+4)(x^2 -4x + 16)\)
What is sum or difference of cubes?If there are two terms which are with power 3 (ie cubed), and they both are in addition or subtraction, then that is called sum or difference of cubes for two terms.
Example: \(a^3 - b^3\) is difference of cubes.
There is a formula too which you can use in case if you need it which goes like this:
\(a^3 + b^3 = (a+b)(a^2 - ab + b^2)\\ \\ a^3 - b^3 = (a-b)(a^2 + ab + b^2)\)
Checking all options whether they result in a sum or difference of cubesOption A: \((x-4)(x^2 + 4x - 16)\)
\((x-4)(x^2 + 4x - 16) = x^3 + 64 -4x^2 + 4x^2 -16x - 16x = x^3 +4^3 -32x\)
Thus, not a sum or difference of cubes
Option B: \((x-1)(x^2 - x+ 1)\)
\((x-1)(x^2 - x+ 1) = x^3 - 1 + x + x -x^2 - x^2 = x^3 - 1 + 2x - 2x^2\)
Thus, not a sum or difference of cubes
Option C: \((x + 1) (x - 1)\)
\((x + 1) (x - 1) = x^2 - 1 + x - x = x^2 - 1\)
It is difference of squares but not of cubes.
Option D: \((x+4)(x^2 -4x + 16)\)
\((x+4)(x^2 -4x + 16) = x^3 + 64 -4x^2 + 16x + 4x^2 - 16x = x^3 + 64 = x^3 + 4^3\\ (x+4)(x^2 -4x + 16) = x^3 + 4^3\)
Thus, it is sum of cubes.
Thus, only Option D: \((x+4)(x^2 -4x + 16)\) is expressible as sum or product of cubes (here it is expressible as sum of cubes \(x^3\) and \(4^3\).
Learn more about sum or difference of cubes here:
https://brainly.com/question/16044387
Answer:
c and e
Step-by-step explanation:
A hiker plans a trip in two sections. Her destination is 18 km away on a bearing of N63'E from her starting position. The first leg of the trip is on a bearing of N13E. The second leg of the trip is 16 km. How long is the first leg? Give the answer to the nearest tenth of a kilometre. The first leg is approximately km. (Do not round until the final answer. Then give your answers to the nearest tenth. Use a comma to separate answers as needed.)
Answers
The hiker plans a trip in two sections, with her destination being 18 km away on a bearing of N63'E from her starting position. The first leg of the trip is on a bearing of N13E. We need to find the length of the first leg.
To find the length of the first leg, we can use trigonometry. Since the bearing is given as an angle relative to the North direction, we can break it down into its components using the right-angled triangle formed by the bearing and the North direction.
In this case, the bearing of N13E can be broken down into a North component (opposite to the angle) and an East component (adjacent to the angle). The North component can be found using the formula: North component = length of leg * sin(bearing angle). The East component can be found using the formula: East component = length of leg * cos(bearing angle).
Once we have the North and East components, we can use them to find the length of the first leg using the Pythagorean theorem: Length of first leg = sqrt((North component)^2 + (East component)^2).
Therefore, to find the length of the first leg, we can follow these steps:
1. Calculate the North component: North component = length of leg * sin(bearing angle).
2. Calculate the East component: East component = length of leg * cos(bearing angle).
3. Calculate the length of the first leg using the Pythagorean theorem: Length of first leg = sqrt((North component)^2 + (East component)^2).
By substituting the given values, we can find the length of the first leg.
to know more about hiker visit:
https://brainly.com/question/33563762
#SPJ11
Find an equation for the line perpendicular to the tangent to the curve y=x3−4x+1 at the point (2,1).
Answers
The equation of the line perpendicular to the tangent to the curve y=x^3-4x+1 at the point (2,1) is y = (-1/8)x + 9/8.
To find the equation of the line perpendicular to the tangent to the curve at (2,1), we need to first find the slope of the tangent line at that point.
The derivative of y=x^3-4x+1 is y'=3x^2-4, so the slope of the tangent line at (2,1) is y'(2) = 3(2)^2-4 = 8.
Since we want the line perpendicular to the tangent, we know that its slope will be the negative reciprocal of the tangent's slope. Therefore, the slope of the line we're looking for is -1/8.
Next, we use the point-slope form of the equation of a line to write the equation of the line with the slope we found and passing through the point (2,1):
y - 1 = (-1/8)(x - 2)
Simplifying and putting the equation in slope-intercept form:
y = (-1/8)x + 9/8
Therefore, the equation of the line perpendicular to the tangent to the curve y=x^3-4x+1 at the point (2,1) is y = (-1/8)x + 9/8.
Learn more about perpendicular here:
https://brainly.com/question/11707949
#SPJ11