Unit 7: right triangles & trigonometry homework 4: trigonometry ratios & finding missing sides
Find KL

Answer:

-20 m/s.

Step-by-step explanation:

The computation of the average speed is shown below:

Given that

The initial velocity of the bus, u = 20 m/s

Aceleration of the bus, -a = 8 m/s²

time of motion, t = 5 s

Now The final velocity of the bus is  

v = u + at

v = 20 + (-8 × 5)

v = 20 - 40

v = -20 m/s.

Answer:

(9 – 4√2)/(9 + 4√2)

Step-by-step explanation:

(1 – 2√2)²/(1 + 2√2)²

Expanding the brackets, we have:

[(1 – 2√2)(1 – 2√2)]/[(1 + 2√2)(1 + 2√2)]

[1 – 2√2 – 2√2 + 8]/[1 + 2√2 + 2√2 +8]

[9 – 4√2]/[9 + 4√2]

Answer:

81/49

Step-by-step explanation:

pls rate as brainliest it will really go along way

Answer: 7.9

Step-by-step explanation:

\(P=2000, r=0.09, n=2\\\\4000=2000\left(1+\frac{0.09}{2} \right)^{2t}\\\\4000=2000(1.045)^{2t}\\\\2=1.045^{2t}\\\\\log_{1.045} 2=2t\\\\t=\frac{\log_{1.045} 2}{2}\\\\t \approx 7.9\)

Answer:

Quadrant II - +

Step-by-step explanation:

3,-4 translated 5 up is 3,1 then 4 units left is -1,1

Answer:

f(x) = 5x – 1

to find the inverse equate f(x) to y

That will be

f(x) = y

>>>>

Interchange the terms >>>

x = 5y - 1

then make y the subject

then we have

5y = x + 1

then if you divide both sides by 5

y = x+1/5

therefore f^-1(x)= x + 1/5

hope this helps you

(Brainliest?)

Step-by-step explanation:

Answer:

Lesser x = -9

Greater x = 9

Step-by-step explanation:

Answer: 150 minutes or 2.5 hours

Step-by-step explanation: subsite the hours with x so you would have 2x=300 if she reads 2 pages a minute in 150 minutes she would have 300 pages

Answer:

Step-by-step explanation:

A. Data of the study: All 45 exercise times there were recorded from the participants in the study

B. Parameter of the study: The average amount of time that all clients exercise in one week.

C. Variable of the study: The amount of time that any given client from the fitness center exercises.

D. Population for the study: All clients at the fitness center.

E. Sample of this study: The 45 client from the fitness center who participated in the study.

F. Statistics of the study: The average amount of time that a sample of clients exercises in one week

Answer:

Step-by-step explanation: 14 11/12 rounds up to 15 and 3 1/6 is closer to 3 so the answer would be 18

Answer:

x = 6, -8

Step-by-step explanation:

If (x - 6)(x + 8) = 0, that would imply that either (x - 6) or (x + 8) would equal zero. Using this, we can find that solving the two equations:

x - 6 = 0

and

x + 8 = 0

would yield the two solutions to the equation.

x - 6 = 0

Add 6 to both sides of the equation.

x = 6

So one of the solutions would be x = 6.

x + 8 = 0

Subtract 8 from both sides of the equation.

x = -8

So the other solution would be x = -8.

The two solutions are x = 6 and x = -8.

I hope you find my answer and explanation to be helpful. Happy studying.

Answer:

x = 6 or x = –8

Step-by-step explanation:

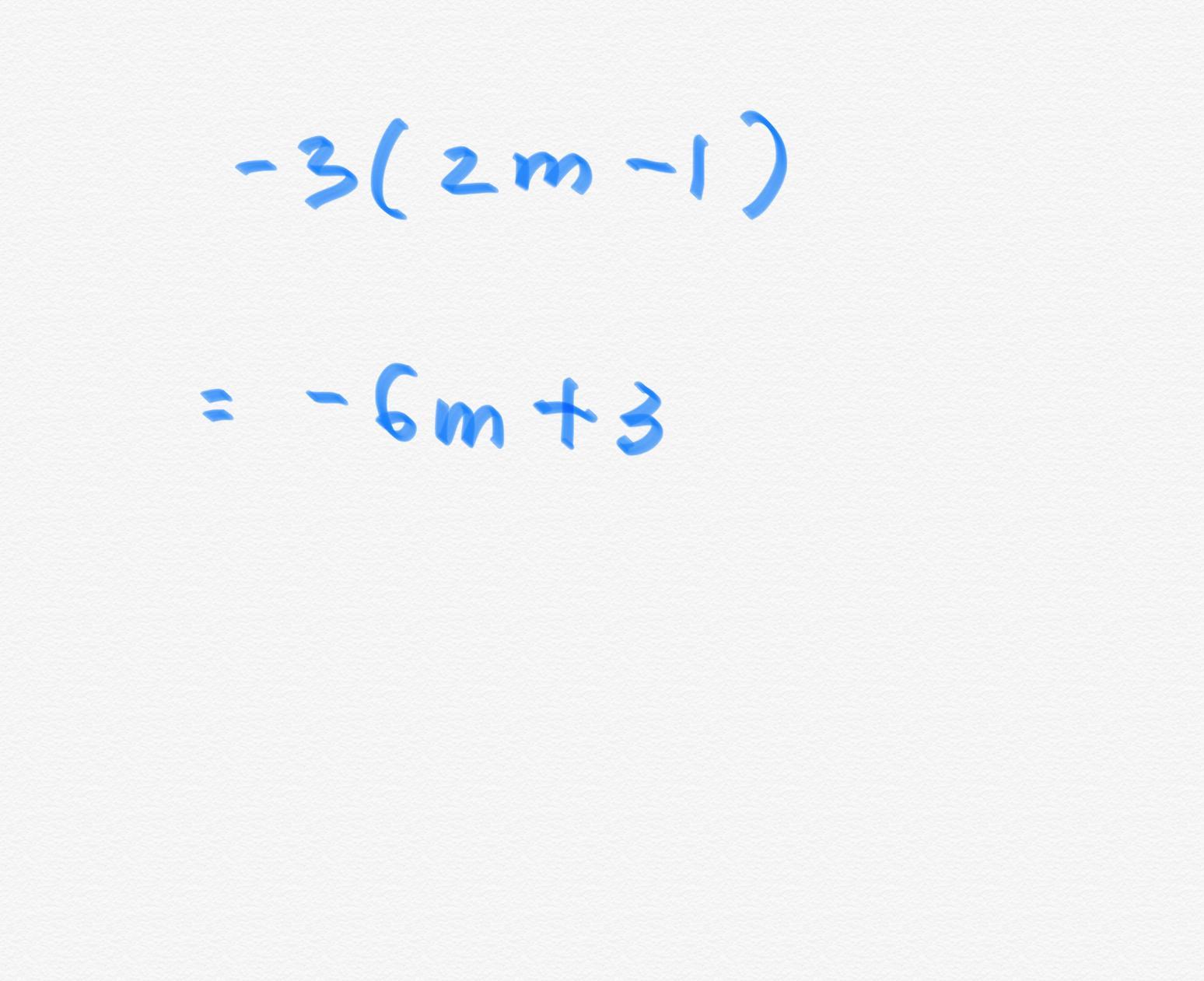
Answer:

36 square units

Step-by-step explanation:

split the figure so that it's a triangle and a rectangle. Find the area of the rectangle (base x height or 6 x 4), which is 24 square units. Then, find the area of the triangle ((base x height)/2 or (6 x 4)/2), which would be 12 units. Then add those units up (24 + 12) and you get 36.

The vertices of the image of triangle ABC under the transformation (x, y)-- (x-3,y+1) followed by a dilation centered at the origin with scale factor 2 are A(2(x1-3),2(y1+1)), B(2(x2-3),2(y2+1)), C(2(x3-3),2(y3+1)).

Transformation in maths is the process of changing the position, size, orientation or shape of a figure or shape. It involves various techniques such as translation, rotation, reflection and scaling.

The transformation (x, y)-- (x-3,y+1) followed by a dilation centered at the origin with scale factor 2 is a combination of a translation and a dilation. A translation is a transformation that moves the shape without changing its size or orientation. In this case, the translation moves the triangle 3 units to the left and 1 unit up. A dilation is a transformation that enlarges or reduces a shape. In this case, the dilation uses a scale factor of 2, so the triangle will be twice as big as it was before.

The vertices of the original triangle ABC are (A(x1,y1), B(x2,y2), C(x3,y3)). After the translation, the vertices will be (A(x1-3,y1+1), B(x2-3,y2+1), C(x3-3,y3+1)). After the dilation, the vertices will be (A(2(x1-3),2(y1+1)), B(2(x2-3),2(y2+1)), C(2(x3-3),2(y3+1)).

For more questions related to scale factor

https://brainly.com/question/2826496

#SPJ1

point (2 ; 0) on Cf so f(2) = 0

point (0 ; 4) on Cf so f(0) = 4

point (-2 ; 0) on Cg so g(-2) = 0

Step-by-step explanation:

I'm sorry

i dont know this particular question

17

18

10

that's the answer

mark me as brainliest please

Answer:

40, 24, 54

Step-by-step explanation:

let the 3 numbers be x, y and z

then

\(\frac{x}{y}\) = \(\frac{5}{3}\) ( cross- multiply )

5y = 3x ( divide both sides by 5 )

y = \(\frac{3}{5}\) x

and

\(\frac{y}{z}\) = \(\frac{4}{9}\) ( cross- multiply )

4z = 9y ( divide both sides by 4 )

z = \(\frac{9}{4}\) y = \(\frac{9}{4}\) × \(\frac{3}{5}\) x = \(\frac{27}{20}\) x

The 3 numbers are now expressed in terms of x , then adding gives

x + \(\frac{3}{5}\) x + \(\frac{27}{20}\) x = 118

multiply through by 20 to clear the fractions

20x + 12x + 27x = 2360

59x = 2360 ( divide both sides by 59 )

x = 40 ← first number

y = \(\frac{3}{5}\) × 40 = 3 × 8 = 24 ← second number

z = \(\frac{27}{20}\) × 40 = 27 × 2 = 54 ← third number

The 3 numbers are 40, 24, 54

\(144x^2-100\)

looking at the original equation, you'll notice that it is a difference of squares therefore the factored form will look like something like this:

\((ax-b)(ax+b)\) where a and b are the two numbers and the x represents the variable.

This would be the factored form:

\((12x-10)(12x+10)\)

It can then be simplified to this:

\(2(6x-5)2(6x+5)\)

and this would be its fully factored form:

\(4(6x-5)(6x+5)\)

Step-by-step explanation:

A = 690ft + B

A + B = 1.384ft

(690ft + B) + B = 1.384ft

2B = 1.384ft - 690ft

2B = 694ft

B = 694ft ÷ 2

B = 347ft

A = 690ft + B

A = 690ft + 347ft

A = 1.037ft

Tower A → 1.037 feet

Tower B → 347feet

The statistical analysis of the data using a two-sample t-test indicates;

(a) B. Yes, the Meters On data appears to have higher speeds

A. No, there does not appear to be any outlier

(b) H₀; \(\mu_{on}\) = \(\mu_{off}\)

H₁; \(\mu_{on}\) > \(\mu_{off}\)

The P-value for the test is about 0.037

A two-sample t-test is used to determine if there is a difference between the means of two independent groups of data.

(a) The average of the data values are;

Ramp meters on;

\(\mu_{on}\) = (29+47+55+38+32+25+42+47+51+36+55+41+43+25+47)/15 ≈ 40.87

\(\mu_{off}\) = (25+25+43+35+36+31+48+37+19+29+22+40+36+50+40)/15 ≈ 34.4

The higher average value for the speed with the Ramp meters on indicates;

B. Yes, the Meters On data appears to have higher speeds

The five number summary are;

Ramp Meters On

Min = 25, Max = 55, Q₁ = 32, Q₂ = 42, Q₃ = 47

IQR = 47 - 32 = 15

Outlier = 47 + 1.5 × 15 = 69.5

32 - 1.5 × 15 = 9.5

Therefore, there are no outliers for the Ramp Meters On

Ramp Meters Off

Min = 19, Max = 50, Q₁ = 25, Q₂ = 36, Q₃ = 40

IQR = 40 - 25 = 15

Outlier = 40 + 1.5 × 15 = 62.5

25 - 1.5 × 15 = 2.5

Therefore, there are no outliers for the Ramp Meters Off data

(b) The null hypothesis is; H₀; \(\mu_{on}\) = \(\mu_{off}\)

The alternative hypothesis is; H₁; \(\mu_{on}\) > \(\mu_{off}\)

(c) The two sample t-test, can be obtained using the formula;

\(t_{cal} = \frac{(\bar{x}_1 - \bar{x}_2)}{\sqrt{(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2} ) } }\)

Where; \(\bar{x}_1\) = 40.87

\(\bar{x}_2\) = 34.40

s₁ = 9.91

s₂ = 9.20

n₁ = n₂ = 15

Therefore; \(t_{cal}\) = 1.8516. The degrees of 15 + 15 - 2 = 28, and the one-tailed hypothesis, indicates, using an online tool;

The p-value is less than 0.05, therefore, the result is significant.

Learn more on two-sample t-test here: https://brainly.com/question/32024330

#SPJ1

The rule of the slope of the line is

(x1, y1) and (x2, y2) are two points on the line

Since the line passes through points (-1, 8) and (12, -5), then

x1 = -1 and y1 = 8

x2 = 12 and y2 = -5

Substitute theses values in the rule above to find m

The slope of the line is -1

Answer:

D. 10b - 2

Step-by-step explanation:

The 2 distributes to the 5b and the -1. So it's 2*5b + 2*(-1) = 10b - 2

Answer:

Step-by-step explanation:

We can use the method of undetermined coefficients to solve this differential equation. First, we will need to find the solution to the homogeneous equation and the particular solution to the non-homogeneous equation.

For the homogeneous equation, we will use the form y"+ky=0, where k is a constant. We can find the solutions to this equation by letting y=e^mx,

y"=m^2e^mx -> (m^2)e^mx+k*e^mx=0, therefore (m^2+k)e^mx=0

(m^2+k) should equal 0 for the equation to have a non-trivial solution. Therefore, m=±i√(k), and the general solution to the homogenous equation is y=A*e^i√(k)x+Be^-i√(k)*x.

Now, we need to find the particular solution to the non-homogeneous equation. We can use the method of undetermined coefficients to find the particular solution. We will let yp=a0+a1x+a2x^2+.... As the derivative of a sum of functions is the sum of the derivatives, we get

yp″=a1+2a2x....yp‴=2a2+3a3x+....

Substituting the general solution into the non-homogeneous equation, we get

a0+a1x+a2x^2+...+2a2x+3a3x^2+...=Y(4)

So, the coefficient of each term in the expansion of the left hand side should equal the coefficient of each term in the expansion of the right hand side. Since there is only one term on the right hand side, we get the recurrence relation:

a(n+1)=Y(n-2)/n^2

From this relation, we can find all the coefficients in the expansion for the particular solution. Using this particular solution, we can find the total solution to the differential equation as the sum of the homogeneous solution and the particular solution.

Answer:

Step-by-step explanation:

To find out how much meat is used in the recipe, we need to add the amounts of ground beef and ground pork together.

Given that the recipe calls for 4/5 pound of ground beef and 1/2 pound of ground pork, we can add these amounts to get the total amount of meat used:

4/5 pound + 1/2 pound

To add these fractions, we need to find a common denominator. The smallest number that both 5 and 2 can divide into is 10. So we can convert the fractions to have a denominator of 10:

4/5 pound = 8/10 pound

1/2 pound = 5/10 pound

Now we can add these fractions with a common denominator of 10:

8/10 pound + 5/10 pound = 13/10 pound

This is the total amount of meat used in the recipe, which is equivalent to 1 and 3/10 pounds, or 1.3 pounds of meat

Answer:

X=2

Step-by-step explanation:

16=8x

Answer:

\(x = 2\)

Step-by-step explanation:

\(x + 4 = 3(3x - 4) \\ x + 4 = 9x - 12 \\ 4 + 12 = 9x - x \\ 16 = 8x \\ \frac{16}{8} = \frac{8x}{8} \\ x = 2\)

Based on the amount predicted to be spent, the hypotheses will be:

The Null Hypothesis is the one that confirms the prediction so in this case it will be that the average shopper will indeed spend $1,007.24.

The Alternate Hypothesis theorizes that the event being predicted will not happen so in this case that would mean that the shopper would not spend $1,007.24.

In conclusion, the null hypothesis confirms and the alternate denies.

Find out more on the null hypothesis at https://brainly.com/question/15980493.

Answer:

we can compare 4 x 3 and 2 x 6, equal to 12. So, we can see that both products are similar and neither is greater.

Step-by-step explanation:

We can use the commutative property of multiplication to see that 3 x 4 is the same as 4 x 3 and 6 x 2 is the same as 2 x 6. When multiplying two numbers, the order of the numbers does not affect the product. Therefore, we can compare 4 x 3 and 2 x 6, equal to 12. So, we can see that both products are similar and neither is greater.

NEED MORE EXPLANATION?

The commutative property of multiplication states that when multiplying two numbers, the order of the numbers does not affect the product. This means that 3 x 4 is the same as 4 x 3, and 6 x 2 is the same as 2 x 6. We can use this property to compare 4 x 3 and 2 x 6, equal to 12. Therefore, we can see that both products are identical and neither is greater.

The value of the test statistic is given as follows:

z = 4.47.

The equation to calculate the test statistic using the z-distribution is given as follows:

\(z = \frac{\overline{p} - p}{\sqrt{\frac{p(1-p)}{n}}}\)

In which:

The parameters for this problem are given as follows:

\(\overline{p} = 0.59, p = 0.5, n = 618\)

p = 0.5 as the most term means that we are testing if the proportion is either less than or greater than 0.5.

Then the test statistic is obtained as follows:

\(z = \frac{\overline{p} - p}{\sqrt{\frac{p(1-p)}{n}}}\)

\(z = \frac{0.59 - 0.5}{\sqrt{\frac{0.5(0.5)}{618}}}\)

z = 4.47.

More can be learned about test statistics at https://brainly.com/question/13873630

#SPJ1

a) The conjugate is (4+√3).

b) The simplest form is 5(4+√3)/13.

What is conjugate?

In mathematics, a pair of binomials with identical phrases that part opposite arithmetic operators in the midst of these similar terms are referred to as conjugates. For instance, the conjugate of p + q is p - q.

When the first type of binomial occurs in the denominator of fractions, conjugates are used to rationalize the denominator.

Here, we have

Given: 5/(4-√3)

We have to find the conjugate of a given term.

a) The conjugate of a given term is

5/(4-√3) = 5/(4-√3) × (4+√3)

Hence, the conjugate is (4+√3).

b) Now, we solve

= 5/(4-√3) × (4+√3)/(4+√3)

= 5(4+√3)/16 - 3

= 5(4+√3)/13

Hence, the simplest form is 5(4+√3)/13.

To learn more about the conjugate from the given link

https://brainly.com/question/17203594

#SPJ1

Answer: I thank it is 200 point in 2 hour

Step-by-step explanation:

Answer:

-6m+3

Step-by-step explanation:

Answer:

An equivalent value is -6m -n +3

Step-by-step explanation:

Given

-3(2m-1)-n   expand

=-6m+3-n

(also equals -6m -n +3 by commutativity)

Answer:Its letter b i think

Step-by-step explanation: