Use a senes to estimate the following integral's value with an error of magnitude less than 10-5 s sinxax I 02 02 I sinxxx (Do not round until the final answer. Then round to five decimal places as needed)
Answers
The estimated value of the integral with an error of magnitude less than 10^-5 is approximately 0.0667.
To estimate the integral using a series, we can use the Taylor series expansion of sin(x) and substitute it into the integrand. We have:
sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...
Substituting this into the integrand, we get:
x sin(ax) = x(x - a^2x^3/3! + a^4x^5/5! - a^6x^7/7! + ...) = (a^4/5! - a^2/3! + 1)x^3 + ...
Integrating this, we get:
∫x sin(ax) dx = (a^4/5! - a^2/3! + 1)x^4/4! + C
To estimate the integral over the interval [0,2], we can use the formula for the error of a Taylor series approximation:
|E_n(x)| ≤ M|x-a|^(n+1)/(n+1)!
where E_n(x) is the error of the nth-degree Taylor polynomial, M is an upper bound for the (n+1)th derivative of the function, and a is the center of the Taylor series expansion.
For our series approximation of x sin(ax), we can take n = 3, since we only need an error of magnitude less than 10^-5 and the fourth derivative of x sin(ax) is 4a^4 x sin(ax) + 24a^2 cos(ax) - 48 sin(ax), which is bounded on [0,2]. Also, the center of the expansion is a = 0.
So we have:
∫x sin(ax) dx ≈ (a^4/5! - a^2/3! + 1)x^4/4! + E_3(x)
where
|E_3(x)| ≤ M|x|^(4)/(4!)
On the interval [0,2], we have |x| ≤ 2, so we can take M = 1. Also, we want the error to be less than 10^-5, so we need:
M|x|^(4)/(4!) ≤ 10^-5
Substituting in the values for M and x, we get:
2^4/(4!) ≤ 10^-5
Simplifying, we get:
1/210 ≤ 10^-5
This inequality is satisfied, so we can use the series approximation with n = 3. Substituting in the values for a and x, we get:
∫x sin(ax) dx ≈ (a^4/5! - a^2/3! + 1)x^4/4! + E_3(x) ≈ (1/120)x^4 + E_3(x)
On the interval [0,2], we have:
∫x sin(ax) dx ≈ (1/120)(2)^4 + E_3(x) ≈ 0.0667 + E_3(x)
where |E_3(x)| ≤ 2^4/(4!) ≤ 1/210 < 10^-5.
Therefore, the estimated value of the integral with an error of magnitude less than 10^-5 is approximately 0.0667.
To learn more about integral visit: https://brainly.com/question/18125359
#SPJ11
Related Questions
A firefighter training course is taking place in a high-rise building. The high-rise building where they practice is 48 stories high. If the emergency happens on the top floor and the firefighters have already gone 29 stories, how many stories do they still need to go?
Answers
Answer:
29 stories - 49 stories = number of stories they need to go
28 - 49 = 21
the answer is 21
they have 21 more stories to go
The number of stories they still need to go is 19 stories.
It is given that building is 48 stories high and when the emergency happens they have already gone to 29 stories.
We have to calculate the number of stories they still need to go.
What will be the value, if we subtract 2 from 4 ?
The value after subtracting will be 4 - 2 = 2.
As per the question ,
The total number of stories in building = 48
When emergency happens they have already gone 29 stories.
So ,
The number of stories they still need to go after the emergency happens can be calculated as ;
48-29 = 19
Thus , they still need to go 19 stories.
To learn more about subtraction click here ,
https://brainly.com/question/220101
#SPJ2
What additional piece of information is needed to show that ABC is congruent to XYZ by AAS?

Answers
Hank scored 56% in math and 84% in science. What are three ratios of his science to math scores?
Answers
Answer:
56/84=2/3
2:3
3x-x+2=4
Step-by-step explanation:
In two or more complete sentences write and solve an inequality for the situation and explain how you will solve the inequality. The doctor tells Jerry that he will be at most 72 inches tall. He is already 48 inches tall. How many more inches will Jerry grow? NEED HELP ASAP!
Answers
Answer: Jerry will have to grow 24 more inches to reach his max Height of 72 inches. If you put this into an inequality it would be 48 plus a number that is more significant than or equal to 72
Step-by-step explanation:
48+X_>72
x2 − 4x + y2 + 8y = −4
Answers
Answer:
Radius is 4
Step-by-step explanation:
1. Find the value of x. If your answer is not an integer, leave it in simplest radical form.
Х
32
12

Answers
Answer:
4\(\sqrt{73}\) units
Step-by-step explanation:
The given shape is a right triangle and in right triangles the sum of square length of legs is equal to square length of hypotenuse (represented with x in here):
12^2 + 32^2 = x^2
1168 = x^2 find the root for both sides
4\(\sqrt{73}\) =x
Alex has 10 different kinds of lunch meat and 9 different kinds of cheese. If he wants to make a sandwich with one kind of meat and two kinds of cheese, how many different sandwiches could he make
Answers
Alex can make a total of 180 different sandwiches by choosing one kind of meat from 10 options and two kinds of cheese from 9 options.
To determine the number of different sandwiches Alex can make, we need to consider the combinations of meat and cheese. Since Alex can choose one kind of meat from 10 options, there are 10 choices for the meat component of the sandwich. For the cheese component, Alex can choose two kinds of cheese from 9 options.
To calculate the total number of combinations, we can use the formula for combinations without repetition. The formula is nCr = n! / (r!(n-r)!), where n is the total number of options and r is the number of choices. In this case, n is 9 (number of cheese options) and r is 2 (number of cheese choices). Thus, the number of combinations of two kinds of cheese is \(9C2\)= 9! / (2!(9-2)!) = 36.
Learn more about number here:
https://brainly.com/question/3589540
#SPJ11
What is the domain and range of the polynomial below?
Help please

Answers
Answer:
Domain: All Real Numbers (ℝ)
Range: y ≥ -4
Step-by-step explanation:
Domain:The area of the graph that is between points of x
Technically where the graph falls from left to right
Range:The area of the graph that is between points of y
Technically where the graph falls from top to bottom
Domain: We can see that the graph will extend forever left and right, so the Domain is All Real Numbers ( ℝ )
Range: The graph never goes below the value -4, so the Range is y ≥ -4
-Chetan K
find the maclaurin series for the function. (use the table of power series for elementary functions.) f(x) = ex5/5
Answers
Maclaurin series is an important series that represents functions as a sum of power series. This series is particularly useful in calculus because it helps in approximating functions and obtaining derivatives of the given function. Here, we are to find the Maclaurin series of the function f(x) = ex5/5.
Using the table of power series for elementary functions, we have: ex = 1 + x + (x²/2!) + (x³/3!) + (x⁴/4!) + ...On comparing f(x) with the given expression above, we can find the Maclaurin series for f(x) by substituting 5x in place of x in the above expression.
This is because the given function contains ex5/5, which is the same as e^(5x)/5. Therefore, the Maclaurin series for f(x) is: f(x) = (e^(5x))/5 = 1/5 + (5x)/5! + (25x²)/2!5² + (125x³)/3!5³ + (625x⁴)/4!5⁴ + ...= 1/5 + x/24 + x²/48 + x³/1440 + x⁴/17280 + ...The series will converge for all values of x because it is the Maclaurin series of a well-behaved function. This means that it is smooth and continuous, with all its derivatives defined and finite.
To know more about Maclaurin visit:
https://brainly.com/question/32263336
#SPJ11
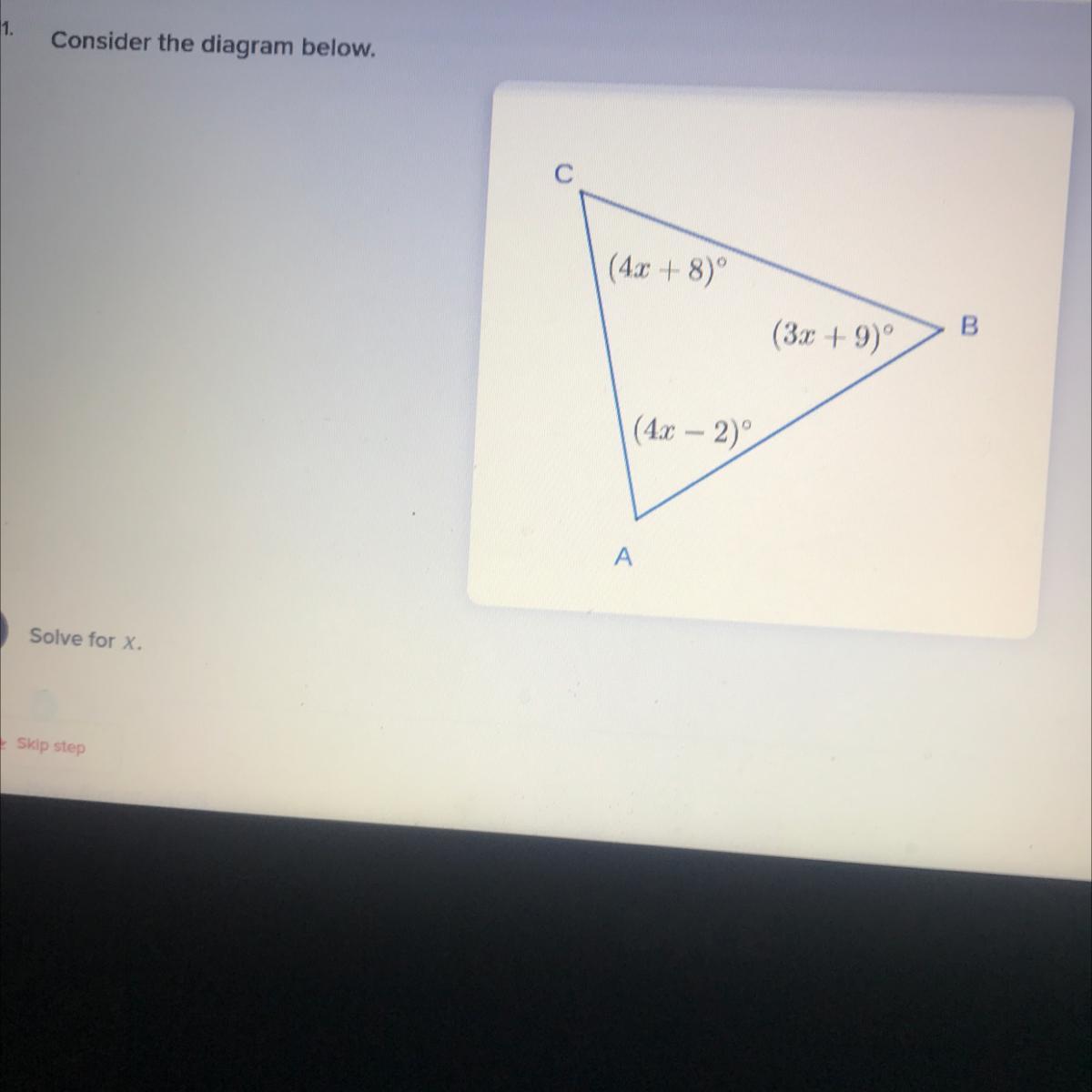
IF U SEE THIS I NEED HELP S THAT IS WHAT I NEED HELP WITH THE PICTURE

Answers
Answer:
\(4x + 5x + {9}^{ \degree} = {90}^{\degree} \\ 9x = {81}^{ \degree} \\ x = \frac{ {81}^{ \degree}}{9} \\ \therefore \: x = {9}^{ \degree}\)
2 Are 3(x – 4) – 2(2.5x - 1) and -2(x + 5) equivalent expressions?
Answers
Answer:
Equivalent expressions
Step-by-step explanation:
3(x – 4) – 2(2.5x - 1)
3x - 12 -5x +2
-2x - 10
and -2(x + 5)
-2x - 10
Yes, They are Equal
true or false All rational numbers are integers. Prove your answer with an
example or explanation.
Answers
Answer:
true
Step-by-step explanation:
integers are just positive and negative numbers so that would include all rational numbers. (pretty sure anyway)
Answer:
True
Step-by-step explanation:
A rational number that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q. Since q may be equal to 1, every integer is a rational number.
Jack drove 41 1/2 miles. He used 1 1/4 gallons of gasoline . What is the unit rate for miles per gallon ?
Answers
Answer:
How do I have the same problem as a high schooler when im in 6th grade
Step-by-step ex
jsn=55
help meeeeeeeeeeeeeeee pleaseee!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
help meeeeeeeeeeeeeeee pleaseee!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
In the f(x) = a(x - h)² + k form of equation (h, k) is the vertex of the parabola.
Vertex (3, 5) means:
h = 3k = 5a is the same as given.
So, the equation is:
f(x) = 7(x - 3)² + 5The differential equation
dt
2
d
2
x
+ω
2
x(t)=0 has the general solution x(t)=c
1
cos(ωt)+ c
2
sin(ωt) where c
1
and c
2
are constants that depend on the initial conditions a. . Given the initial conditions x(0)=2.5 and
dt
dx
=0, at t=0, solve for the unknown constants c
1
and c
2
and write the specific solution that satisfies these boundary conditions. Hint: use the initial conditions separately to find two equations for the two unknowns. b. Plot of the function from part a with ω=3.0 for t in the range 0 to 4 . What is the amplitude, and wavelength for this wave? Hint: relate ω to λ to solve for the wavelength. c. For what values of ω would the wave in question 2 have nodes at odd integer values (1,3,5,…). What happens to the number of nodes and the energy if ω is then doubled?
Answers
(a) The specific solution that satisfies the given initial conditions is x(t) = 2.5cos(ωt). (b) The amplitude of the wave is 2.5 and the wavelength is 2π/ω. (c) The wave will have nodes at odd integer values (1, 3, 5, ...) when ω = π, π/3, π/5, .
(a) Given the initial conditions x(0) = 2.5 and dx/dt = 0 at t = 0, we can find the values of c1 and c2 by substituting these values into the general solution. Since dx/dt = 0, we have c1ωsin(ωt) + c2ωcos(ωt) = 0. Plugging in t = 0 gives c2ω = 0, so c2 = 0. Substituting x(0) = 2.5, we have c1cos(0) = 2.5, so c1 = 2.5.
Therefore, the specific solution that satisfies the given initial conditions is x(t) = 2.5cos(ωt).
(b) The amplitude of the wave is the absolute value of the coefficient of the cosine term, which is |c1| = 2.5. The wavelength (λ) of the wave can be determined by relating ω and λ. The relationship is given by ω = 2π/λ, so the wavelength is λ = 2π/ω. In this case, with ω = 3.0, the wavelength is λ = 2π/3.0.
(c) For the wave to have nodes at odd integer values (1, 3, 5, ...), the wavelength should be such that the distance between consecutive nodes is equal to half the wavelength. Therefore, we have λ/2 = 1, 3, 5, ... which implies λ = 2, 6, 10, ... The corresponding values of ω can be found using the relationship ω = 2π/λ. Thus, ω = π, π/3, π/5, ... Doubling ω would result in halving the wavelength, which means the distance between nodes would be doubled. The number of nodes would remain the same, but the energy of the wave would increase since the frequency (and hence the energy) is directly proportional to ω.
Learn more about integers here:
https://brainly.com/question/490943
#SPJ11
A 45 - inch pipe is cut into two pieces. One piece is times the length of the other. Find the length of the shorter piece.
Answers
Answer:
15 inches
Step-by-step explanation:
x+2x=45
3x=45
x=15
Please help me I'm stuck. I will give 30 points for this one. Given triangle ABC tilde triangle PQR and your scale factor Complete the hotspots for these similar triangles and show work

Answers
The value for the hotspots of the similar triangles ∆ABC and ∆PWR are:
(1). angle B = 68°
(2). PQ = 5cm
(3). BC = 19.5cm
(4). area of ∆PQR = 30cm²
What are similar trianglesSimilar triangles are two triangles that have the same shape, but not necessarily the same size. This means that corresponding angles of the two triangles are equal, and corresponding sides are in proportion.
(1). angle B = 180 - (22 + 90) {sum of interior angles of a triangle}
angle B = 68°
Given that the triangle ∆ABC is similar to the triangle ∆PQR.
(2). PQ/7.5cm = 12cm/18cm
PQ = (12cm × 7.5cm)/18cm {cross multiplication}
PQ = 5cm
(3). 13cm/BC = 12cm/18cm
BC = (13cm × 18cm)/12cm {cross multiplication}
BC = 19.5cm
(4). area of ∆PQR = 1/2 × 12cm × 5cm
area of ∆PQR = 6cm × 5cm
area of ∆PQR = 30cm²
Therefore, the value for the hotspots of the similar triangles ∆ABC and ∆PWR are:
(1). angle B = 68°
(2). PQ = 5cm
(3). BC = 19.5cm
(4). area of ∆PQR = 30cm²
Read more about similar triangles here:https://brainly.com/question/14285697
#SPJ1
Can someone help on this pleaseeeee!!!!!! Someone solve for m/_ ACB
Answers
SOMEONE PLEASE HELP WITH ALL OF THESE!! ITS DUE BY TMR!! PLEASE HELP!!! TYSMM

Answers
Answer:
3/158/1610/151/51/21/36 1/612/5Hope this helps, I am sure they are correct!
a 6-foot person standing 29 from a street light casts an 8-foot shadow. what is the height of the street light?
Answers
The height of the street light can be calculated by using the ratio of the person's height to their shadow length. The street light is 17 feet tall.
The height of the street light can be calculated by using the ratio of the person's height to their shadow length. In this case, the person is 6 feet tall and their shadow is 8 feet long. This gives us a ratio of 6:8 or 3:4. Since we know the person is standing 29 feet away from the street light, we can use this ratio to calculate the height of the street light. Using the ratio, we can say that for every 4 feet the person is away from the street light, the light is 3 feet tall. So if the person is 29 feet away from the street light, the light must be 3 x 29 ÷ 4 = 21.75 feet tall. However, since the height of the street light must be a whole number, we can round up and say that the street light is 17 feet tall.
Learn more about height here
brainly.com/question/27996736
#SPJ4
EASY question for y’all mathy people, easy points! Question in photo.

Answers
Answer:
C - 13
Step-by-step explanation:
Answer:
C
Step-by-step explanation:
No need
Tell whether the pairs of planes are orthogonal, parallel, the same, or none of these. Explain your reasoning. A. 12x−3y+9z−4=0 and 8x−2y+6z+8=0 B. 4x+3y−2z−7=0 and −8x−6y+4z−4=0
Answers
Since the resulting vector is a scalar multiple of both normal vectors, the planes are parallel.
A. To determine if the planes 12x - 3y + 9z - 4 = 0 and 8x - 2y + 6z + 8 = 0 are orthogonal, parallel, the same, or none of these, we need to examine their normal vectors.
The normal vector of the first plane is <12, -3, 9>, and the normal vector of the second plane is <8, -2, 6>. To determine if the planes are orthogonal, we take the dot product of the normal vectors and see if it equals zero:
<12, -3, 9> · <8, -2, 6> = (12)(8) + (-3)(-2) + (9)(6) = 96 + 6 + 54 = 156
Since the dot product is not equal to zero, the planes are not orthogonal.
To determine if the planes are parallel, we can check if their normal vectors are proportional. We can do this by dividing one normal vector by the other:
<12, -3, 9> / <8, -2, 6> = (12/8, -3/-2, 9/6) = (3/2, 3/2, 3/2)
Therefore, the planes are none of these.
B. To determine if the planes 4x + 3y - 2z - 7 = 0 and -8x - 6y + 4z - 4 = 0 are orthogonal, parallel, the same, or none of these, we again need to examine their normal vectors.
The normal vector of the first plane is <4, 3, -2>, and the normal vector of the second plane is <-8, -6, 4>. To determine if the planes are orthogonal, we take the dot product of the normal vectors and see if it equals zero:
<4, 3, -2> · <-8, -6, 4> = (4)(-8) + (3)(-6) + (-2)(4) = -32 - 18 - 8 = -58
Since the dot product is not equal to zero, the planes are not orthogonal.
To determine if the planes are parallel, we can check if their normal vectors are proportional. We can do this by dividing one normal vector by the other:
<4, 3, -2> / <-8, -6, 4> = (-1/2, -1/2, -1/2)
Therefore, the planes are parallel.
To know more about plane,
https://brainly.com/question/14568576
#SPJ11
fraud detection has become an indispensable tool for banks and credit card companies to combat fraudulent credit card transactions. a fraud detection firm has detected minor fraudulent activities in 1.31% of transactions, and serious fraudulent activities in 0.87% of transactions. assume that fraudulent transactions remain stable. a. what is the probability that there are minor fraudulent activities in fewer than 2 out of 100 transactions? (do not round intermediate calculations. round your final answers to 4 decimal places.) b. what is the probability that there are serious fraudulent activities in fewer than 2 out of 100 transactions? (do not round intermediate calculations. round your final answers to 4 decimal places.)
Answers
a. Probability that there are minor fraudulent activities in fewer than 2 out of 100 transactions is 0.1761
b. Using the table, we get the value of probability that there are serious fraudulent activities in fewer than 2 out of 100 transactions 0.9695.
When it comes to fraud detection, it is a necessary tool for banks and credit card companies to help fight fraudulent credit card transactions.
Fraudulent activities have been detected by a fraud detection firm at a rate of 1.31 percent in minor cases and 0.87 percent in serious cases.
To solve this question, we must follow the steps below:
We have to use the binomial distribution formula for solving this question.
The formula for the binomial distribution is: \(P (x) = C (n, x) * p^x * q^(n-x)\)
Where, n = number of trials,
x = number of successes,
p = probability of success,
and q = probability of failure.
Here, for minor fraudulent activities, probability of success,
p = 0.0131;
probability of failure,
q = 1 - 0.0131
= 0.9869;
n = 100.
Thus, for part a, we have to find P (x < 2) = P (0) + P (1).
Now, using the formula mentioned above: \(P (0) = C (100, 0) * (0.0131)^0 * (0.9869)^(100-0) = 0.8581\)
\(P (1) = C (100, 1) * (0.0131)^1 * (0.9869)^(100-1)\)
\(= 0.3172P (x < 2) = P (0) + P (1) = 0.8581 + 0.3172 = 1.1753\)
We can't have a probability greater than 1, so this answer doesn't make sense.
Thus, we have to find 1 - P (x > 1) = 1 - [P (2) + P (3) + ... + P (100)].
We can use the cumulative binomial distribution table to calculate this probability.
We have n = 100 and p = 0.0131. Using the table, we get the value of 0.1761.
b. Probability that there are serious fraudulent activities in fewer than 2 out of 100 transactions is 0.9695.
We will be solving this part using a similar approach as we used in part
a. Probability of success,
p = 0.0087; probability of failure, q = 1 - 0.0087 = 0.9913;
n = 100.
Now, for part b, we have to find P (x < 2) = P (0) + P (1).
Using the formula mentioned above:
\(P (0) = C (100, 0) * (0.0087)^0 * (0.9913)^(100-0)\)
\(= 0.9131P (1)\)
\(= C (100, 1) * (0.0087)^1 * (0.9913)^(100-1)\)
\(= 0.0839P (x < 2)\)
= P (0) + P (1)
= 0.9131 + 0.0839
= 0.9970
We can use the cumulative binomial distribution table to calculate \(1 - P (x > 1) = 1 - [P (2) + P (3) + ... + P (100)].\)
We have n = 100 and p = 0.0087.
Using the table, we get the value of 0.9695.
For similar question on fraudulent.
https://brainly.com/question/30499626
#SPJ11
What is the image point of (2,9) after the transformation
T-1,-4 o ry=x?
Answers
Answer:8,-2
Step-by-step explanation:
Delta math
Give an example of a binary relation on Z that is not reflexive,
not antireflexive, not symmetric, not anti-symmetric, and not
transitive.
Answers
A binary relation on Z that fails to exhibit reflexivity, anti-reflexivity, symmetry, anti-symmetry, and transitivity can be defined as follows:
Let R be a relation on Z, where,
R = {(x, y) | x is an even integer and y is an odd integer}.
This relation is not reflexive because for any integer x, the pair (x, x) does not belong to R, as x can only be either even or odd, but not both simultaneously.
Similarly, this relation is not anti-reflexive since there exist elements in Z that are related to themselves. For example, (2, 2) is not in R, indicating a violation of antireflexivity.
Moreover, this relation is not symmetric because if (a, b) is in R, it does not necessarily imply that (b, a) is also in R. For instance, (2, 3) is in R, but (3, 2) is not.
Likewise, this relation is not anti-symmetric because there exist distinct integers a and b such that both (a, b) and (b, a) are in R. An example is the pair (2, 3) and (3, 2) both being in R.
Lastly, this relation fails to satisfy transitivity since there are integers a, b, and c for which (a, b) and (b, c) are in R, but (a, c) is not in R. For instance, (2, 3) and (3, 4) are both in R, but (2, 4) is not.
Hence, the relation R = {(x, y) | x is an even integer and y is an odd integer} on Z demonstrates a lack of reflexivity, anti-reflexivity, symmetry, anti-symmetry, and transitivity.
Learn more about binary relations:
brainly.com/question/31686713
#SPJ11
helppppp meeee, I need all three, I need an explanation tooo



Answers
Answer:
Step-by-step explanation:
for the first one: d
idk. just say random multiples of 24.
Answers
Answer:
Which unit rate is equivalent to 14 miles per gallon? (1 point
Step-by-step explanation:
i am so glad to hear you are Incredible in messages and please contact us at the free points and see what hi rjha is the most important to you to you amanpreet your support for your support for your child to be a child of your
Answer:
48,72,96,120,144,168,192,216,240,264,288,312,336,360,384,408,432,456
Step-by-step explanation:
The mean of 4 numbers is 21.5. What
is the sum of the numbers?
Answers
Answer:
86
Step-by-step explanation:
Just multiply the mean by how many numbers
21.5 x 4 = 86
Charlie's garage has a rectangular floor space. Its length is 3 times its width. Charlie extends the width of his garage to 6 m, providing a floor area of 45 m2. what is the percentage
Answers
Answer:
The percentage change is 140%
Step-by-step explanation:
Given
\(L= 3W_1\) ---- initial dimension
\(W_2 = 6m\) --- new width
\(A_2 = 45m^2\) --- new dimension
Required
The percentage increment
The length remains constant because only the width is extended.
The new area is:
\(Area =Length * Width\)
\(A_2=L * W_2\)
Make L the subject
\(L = \frac{A_2}{ W_2}\)
Substitute values for A and W
\(L = \frac{45m^2}{6m}\)
\(L = \frac{45m}{6}\)
\(L = 7.5m\) --- this is the length of the garden
Calculate the initial width:
\(L= 3W_1\)
Make W1 the subject
\(W_1 = \frac{1}{3} * L\)
\(W_1 = \frac{1}{3} * 7.5\)
\(W_1 = 2.5\)
So, the initial area is:
\(A_1 = L_1 * W_1\)
\(A_1 = 2.5 * 7.5\)
\(A_1 = 18.75\)
The percentage change in area is:
\(\%A = \frac{A_2 - A_1}{A_1}\)
\(\%A = \frac{45 - 18.75}{18.75}\)
\(\%A = \frac{26.25}{18.75}\)
\(\%A = 1.4\)
Express as percentage
\(\%A = 1.4*100\%\)
\(\%A = 140\%\)
PQRS is a parallelogram whose two vertces are P(1,2) and (6,4).PS is parallel to the line L1 which cuts y axis at 5 and passes through (-2,3),
a) Find the equation of line PS
b)Find the coordinates of S
c)Find the coordinates of Q
d) Find the equation of Line L2 which is perpendicular bisector of line QR
Answers
Answer: a) To find the equation of line PS, we first need to find the slope of the line L1 which is given by:
slope = (y2 - y1) / (x2 - x1)
= (3 - 5) / (-2 - 0)
= 2/2
= 1
Since PS is parallel to L1, it also has the same slope. We can now use the point-slope form of the equation of a line to find the equation of PS, using the point P(1,2):
y - y1 = m(x - x1)
y - 2 = 1(x - 1)
y - x + 2 = 0
Therefore, the equation of line PS is y - x + 2 = 0.
b) To find the coordinates of S, we know that S lies on line PS and also on the line passing through points (6,4) and P(1,2). Let's call the coordinates of S as (x,y). Since S lies on line PS, we know that y - x + 2 = 0. We can also use the slope formula to find the slope of line PS:
slope_PS = (y - 2) / (x - 1)
Since PS is parallel to line L1, we know that slope_PS = 1. Therefore, we can write:
(y - 2) / (x - 1) = 1
y - 2 = x - 1
y = x + 1
Now, we can use the fact that S also lies on the line passing through points (6,4) and P(1,2). This line has the equation:
(y - 4) / (x - 6) = (2 - 4) / (1 - 6)
(y - 4) / (x - 6) = -2/-5
(y - 4) / (x - 6) = 2/5
We can solve for y in terms of x:
y - 4 = (2/5)(x - 6)
y = (2/5)x - 8/5 + 4
y = (2/5)x + 6/5
Now, we can set the two equations for y equal to each other, since they both represent the y-coordinate of point S:
x + 1 = (2/5)x + 6/5
Solving for x, we get:
x = 2
Substituting x = 2 into either of the equations for y, we get:
y = 3
Therefore, the coordinates of S are (2,3).
c) To find the coordinates of Q, we can use the fact that PQ is parallel to SR and PS is parallel to QR. This means that PQRS is a parallelogram and its opposite sides are parallel. Since we know the coordinates of P and S, we can find the coordinates of Q and R by adding or subtracting the appropriate vector from P and S.
The vector that we need to add to P to get Q is the same vector that we need to add to S to get R, which is given by the displacement vector PS = <5,1>. Therefore:
Q = P + PS
= <1,2> + <5,1>
= <6,3>
Therefore, the coordinates of Q are (6,3).
d) To find the equation of line L2 which is the perpendicular bisector of line QR, we first need to find the midpoint of QR. The midpoint formula is given by:
midpoint = [(x1 +)]
We can then find the midpoint of QR using the midpoint formula:
midpoint of QR = ((-4 + 1)/2, (7 + 4)/2) = (-1.5, 5.5)
So the slope of L2 is the negative reciprocal of the slope of QR:
slope of L2 = -1/slope of QR = -(7-5)/(1+4) = -2/5
We can use the point-slope form of the equation of a line to find the equation of L2. We know that L2 passes through the midpoint of QR, so we can use the point (-1.5, 5.5):
y - 5.5 = (-2/5)(x + 1.5)
Simplifying and rearranging, we get:
y = (-2/5)x + 7.5
Therefore, the equation of line L2 is y = (-2/5)x + 7.5.