Use the concept of the definite integral to find the total area between the graph off(x) and thex-axis, by taking the limit of the associated right Riemann sum. Write the exact answer. Do not round. (Hint: Extra care isneeded on those intervals wheref(x) < 0. Remember that the definite integral represents a signed area.)f(x) = 3x + 3 on [0, 2]

Answers
ANSWER
15 square unit.
EXPLANATION
Step 1:
Recall that the right endpoint Riemann sum for
\(\begin{gathered} ^{}\int ^b_af(x)dx\text{ is given by } \\ \frac{b-a}{n}\sum ^n_{k\mathop=1}f(a+\frac{b-a}{n}k) \end{gathered}\)
Step 2:
Note, if f(x) is continuous, then:
\(\lim _{n\to\infty}\frac{b-a}{n}\sum ^n_{k\mathop{=}1}f(a+\frac{b-a}{n}k)\text{ = }^{}\int ^b_af(x)dx\text{ }\)Step 3:
Now, applying the limit of the Reimann sums to evaluate the integral:
\(^{}\int ^2_0(3x+3)dx\text{ }\)Please, carefully check my working:
Hence, using the concept of the definite integral, the total area between the graph of f(x) and the x-axis by taking the limit of the associated right Riemann sum is 15 square unit.

Related Questions
Note: Enter your answer and show all the steps that you use to
solve this problem in the space provided.
You have a credit card with a balance of $1,367.90 at a 9.5%
APR. You pay $400.00 each month on the due date until the
card is paid off. How many months does it take to pay off the
card, and what is the total amount paid including interest?
Be sure to include in your response:
• the answer to the original question
. the mathematical steps for solving the problem
demonstrating mathematical reasoning
Answers
Given statement solution is :- It takes 4 months to pay off the card, and the total amount paid, including interest, is $1600.
To determine the number of months it takes to pay off the credit card and the total amount paid, including interest, we can follow these steps:
Step 1: Calculate the monthly interest rate.
The APR (Annual Percentage Rate) is given as 9.5%. To find the monthly interest rate, we divide this by 12 (the number of months in a year):
Monthly interest rate = 9.5% / 12 = 0.0079167
Step 2: Determine the monthly payment.
The monthly payment is given as $400.
Step 3: Calculate the interest and principal paid each month.
The interest paid each month can be calculated by multiplying the monthly interest rate by the current balance.
Principal paid = Monthly payment - Interest paid
Step 4: Track the remaining balance each month.
Starting with the initial balance of $1,367.90, subtract the principal paid each month to determine the new balance.
Step 5: Repeat Steps 3 and 4 until the balance reaches zero.
Continue calculating the interest and principal paid each month, updating the balance, until the remaining balance becomes zero.
Step 6: Determine the total number of months and the total amount paid.
Count the number of months it takes to reach a balance of zero. Multiply the number of months by the monthly payment ($400) to find the total amount paid.
Let's calculate the number of months and the total amount paid, including interest:
Month 1:
Interest paid = 0.0079167 * $1,367.90 = $10.84
Principal paid = $400 - $10.84 = $389.16
New balance = $1,367.90 - $389.16 = $978.74
Month 2:
Interest paid = 0.0079167 * $978.74 = $7.75
Principal paid = $400 - $7.75 = $392.25
New balance = $978.74 - $392.25 = $586.49
Month 3:
Interest paid = 0.0079167 * $586.49 = $4.64
Principal paid = $400 - $4.64 = $395.36
New balance = $586.49 - $395.36 = $191.13
Month 4:
Interest paid = 0.0079167 * $191.13 = $1.51
Principal paid = $400 - $1.51 = $398.49
New balance = $191.13 - $398.49 = -$207.36 (Paid off)
It takes 4 months to pay off the credit card. Now, let's calculate the total amount paid, including interest:
Total amount paid = 4 * $400 = $1600
Therefore, it takes 4 months to pay off the card, and the total amount paid, including interest, is $1600.
For such more questions on Credit Card Payoff
https://brainly.com/question/26867415
#SPJ8
$15,000 is invested at a rate of 8% compounded quarterly. Identify the compound interest function to model the situation. Then find the balance after 10 years.
Answers
Answer:
A = 15000(1.02)^4t ; $33,120.59
Which expression is equivalent to 36 + 18
O 3(12 + 6).
O 3(33 + 6)
Submi
O 6(6 + 18)
O 6(6+2)
Answers
Robert has some nickels and some dimes. He has a maximum of 29 coins worth no less than $2.20 combined. If Robert has 10 nickels, determine all possible values for the number of dimes that he could have. Your answer should be a comma separated list of values. If there are no possible solutions, submit an empty answer.
Answers
Robert has 10 nickels, which means he already has 10 coins. We need to find the possible values for the number of dimes he could have.
Let's assume Robert has x dimes.
The value of 10 nickels is 10 * $0.05 = $0.50.
The value of x dimes is x * $0.10 = $0.10x.
The total value of the coins is at least $2.20. So we can write the inequality:
$0.50 + $0.10x ≥ $2.20
Now let's solve this inequality for x:
$0.10x ≥ $2.20 - $0.50
$0.10x ≥ $1.70
x ≥ $1.70 / $0.10
x ≥ 17
Therefore, the possible values for the number of dimes Robert could have are 17 or greater.
So, the comma-separated list of possible values for the number of dimes is: 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29.
Note: We have considered the maximum limit of 29 coins mentioned in the problem, so any value of x greater than or equal to 17 and less than or equal to 29 would satisfy the given conditions.
Robert's dimes are anywhere between 17 and 19.
Explanation:Nickels
are worth 5 cents, and
dimes
are worth 10 cents. Since Robert has 10 nickels, he already has 50 cents. To reach a minimum of $2.20, or 220 cents, Robert needs at least 170 more cents. Because each dime is worth 10 cents, he needs a minimum of 17 dimes. If he has a maximum of 29 coins in total, subtracting the 10 nickels means that he can have up to 19 dimes. So, Robert could have anywhere between 17 and 19 dimes.
Learn more about Counting Coins here:https://brainly.com/question/32061237
#SPJ3
Which equation is not equivalent

Answers
Answer:
C
Step-by-step explanation:
(2x+3)(x+4) = 2x² + 8x + 3x + 12
= 2x² + 11x + 12 ≠ 2x² + 10x + 12
SOMEBODY PLEASE HELP ASAP

Answers
Answer:
40
Step-by-step explanation:
\(\frac{RW}{24}=\frac{30}{18} \\ \\ RW=40\)
Two parallel lines are crossed by a transversal. What is the value of x? x = 40 x = 70 x = 110 x = 130.
Answers
If two parallel lines are crossed by a transversal, the value of x is option (b) x = 70 degrees
When two parallel lines are intersected by a transversal, eight angles are formed. Two of these angles are vertical angles, which are opposite angles that share the same vertex and are formed by the intersection of two lines.
Vertical angles are always congruent, meaning they have the same measure. This is a geometric property that is true regardless of the angle's degree measurement.
In this problem, one of the vertical angles is given to be 70 degrees. Therefore, the other vertical angle must also have a measure of 70 degrees. This means that the value of x, which is the measure of one of the vertical angles, is also 70 degrees.
So, correct option is (b) x = 70 degrees.
Learn more about vertical angles here
brainly.com/question/18441229
#SPJ4
The given question is incomplete, the complete question is:
Two parallel lines are crossed by a transversal. What is the value of x? a) x = 40 b) x = 70 c) x = 110 d) x = 130.

825 use each digit once. make the smallest 3digit number
Answers
Step-by-step explanation:
Given: To make smallest 3-digit number of 825.
To find: The smallest 3-digit number of 825.
Solution: We can make the smallest 3-digit number of 825 by separating the numbers and arranging it to ascending order. The given number is 825. ...
Final answer: The smallest 3-digit number of 825 is 258.
hope it helps
Answer:
258
Step-by-step explanation:
We are given 3 numbers:
8 2 5
And we are asked to find the smallest 3 digit number using those 3 digits above.
To make the smallest number, place the numbers in value from least to greatest:
2 5 8
This is your 3 digit number: 258.
Hope this helps! :)
Which triangle is a reflection of the green triangle
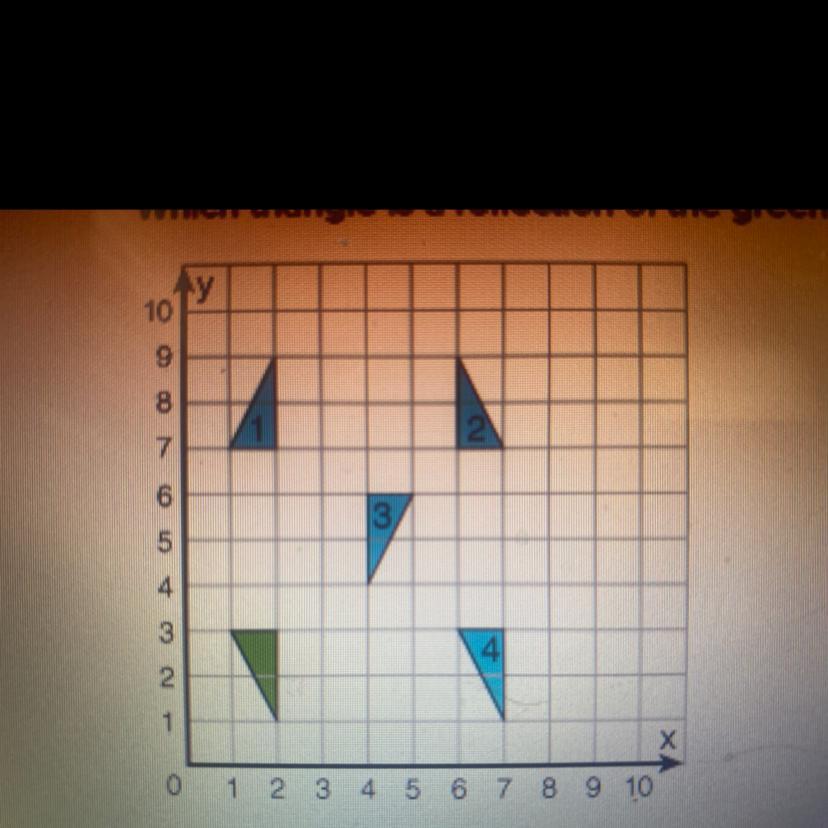
Answers
Tthe triangle that is a reflection of the green triangle is figure 1
Which triangle is a reflection of the green triangleFrom the question, we have the following parameters that can be used in our computation:
The figures
Where, we have:
Figure 1 and the green figure have the opposite orientationFigure 1 and the green figure have the same sizeThis means that the triangle that is a reflection of the green triangle is figure 1
Read more about transformation at
brainly.com/question/4289712
#SPJ1
Solve for f.
3<
f
–
1
+7
Answers
Answer:
F will be +5
Step-by-step explanation:
using the numbers 3 5 9
9 4 and 6 make a equation that is equal to 100
Answers
Answer:
5 + 5 + 9 + 5 + 9 + 3 + 9 + 9 + 3 + 4 + 4 + 9 + 3 + 4 + 9 + 5 + 5
Step-by-step explanation:
NEED HELP PLZ
This probability distribution shows the
typical grade distribution for a Geometry
course with 35 students.
Grade
A
B C D
F
Frequency 5
10
15
3
2
Using the frequencies given, find the
probability that a student earns a grade of A.
p = [?]
Enter a decimal rounded to the nearest hundredth.
Enter

Answers
Answer:
0.14
Step-by-step explanation:
From the question given above, the following data were obtained:
Grade A = 5
Grade B = 10
Grade C = 15
Grade D = 3
Grade F = 2
Sample space (S) = 35
Probability of getting grade A, P(A) =?
The probability that a student obtained a grade of A can be obtained as follow:
Probability of getting grade A, P(A) =
Event of A (nA) / Sample space, (nS)
P(A) = nA/nS
P(A) = 5/35
P(A) = 0.14
Thus, probability that a student obtained a grade of A is 0.14
NO LINKS!! URGENT HELP PLEASE!!!
Please help me with Growth rate and Initial Value only

Answers
Answer:
growth rate: 4
y-value: 19
equation: y=4x+19
Step-by-step explanation:
Growth Rate:
The growth rate of a linear function is constant. This means that the function will increase or decrease by the same amount for every unit increase in x.
This can be found by dividing the change in y-values by the change in x-values.
For the question:
The change in y-values is 11-7=4,
and the change in x-values is +1.
Therefore, the growth rate is 4.
\(\hrulefill\)
Initial Value: The initial value of a linear function is the value of the function when x is 0.
In this case, the initial value is 19.
This can be found by looking at the y-value of the point where x is 0.
In this case, the y-value is 19.
\(\hrulefill\)Equation: The equation of a linear function is y = mx + b, where m is the slope and b is the y-intercept.
Using the table you provided, we can find the slope by using two points on the line.
Let’s use (-3, 7) and (1, 23).
The slope is (y2-y1)/(x2-x1)=(23-7)(1-(-3)=16/4=4
Now,
Taking 1 point (-3,7) and slope 4.
we can find the equation by using formula:
y-y1=m(x-x1)
y-7=4(x+3)
y=4x+12+7
y=4x+19
Therefore, the equation of the given table is y=4x+19\(\hrulefill\)
Answer:
Growth rate: 4
Initial value: 19
Equation: y = 4x + 19
Step-by-step explanation:
The slope of a linear function represents its growth rate.
Therefore, the growth rate of a linear function can be found using the slope formula.
Substitute two (x, y) points from the table into the slope formula, and solve for m. Substituting points (0, 19) and (1, 23):
\(\textsf{slope}\:(m)=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{23-19}{1-0}=\dfrac{4}{1}=4\)
Therefore, the growth rate of the linear function is 4.
The initial value of a linear function refers to the y-intercept, which is the value of the y when x = 0.
From inspection of the given table, y = 19 when x = 0.
Therefore, the initial value of the linear function is 19.
To write a linear equation given the growth rate (slope) and initial value (y-intercept), we can use the slope-intercept formula, which is y = mx + b. The slope is represented by the variable m, and the y-intercept is represented by the variable b.
As the growth rate of the given linear function is 4, and the initial value is 19, substitute m = 4 and b = 19 into the slope-intercept formula to create the equation of the linear function represented by the given table:
\(\boxed{y=4x+19}\)
for each triangle, calculate (vertical side) ÷ (horizontal side)
Answers
Triangle RST = 2/4 = 1/2
Triangle XYZ = 3/6 = 1/2
If a movie ticket cost $5 in 1994, and the CPI for 1994 was .5, what is the price of the movie ticket, adjusted for inflation?
Answers
Adjusted price = Nominal price x (CPI in the base year / CPI in the current year)
The base year is usually set to 100 for CPI calculations, so we need to multiply the CPI by 100:
Adjusted price = $5 x (50 / 100) = $2.50
Therefore, the price of the movie ticket, adjusted for inflation, would be $2.50 in today's dollars.
The price of the movie ticket, adjusted for inflation, is $10.
Explanation:To calculate the price of the movie ticket, adjusted for inflation, you need to use the CPI (Consumer Price Index) for the year 1994. The CPI for 1994 was 0.5. The formula to adjust for inflation is:
Adjusted Price = Original Price / CPI
In this case, the original price is $5 and the CPI is 0.5. So, the adjusted price is:
Adjusted Price = $5 / 0.5 = $10
Therefore, the price of the movie ticket, adjusted for inflation, is $10.
Learn more about Inflation here:https://brainly.com/question/34016204
#SPJ11
A right triangle table top has legs that
measure 3.5 feet. What is the perimeter
of the table top?
Answers
Answer:
i
Step-by-step explanation:
Answer:
12 feet
Step-by-step explanation:
use the pythagorean theorem to figure out what the hypotenuse is
3.5^2+3.5^2=x^2
12.25+12.25=x^2
25=x^2
x=5
now that you know the hypotenuse, you can find the perimeter by adding up all the sides
3.5+3.5+5=12
Find the maximum value of s = xy + yz + xz where x+y+z=9.
Answers
From the constraint, we have
\(x+y+z=9 \implies z = 9-x-y\)
so that \(s\) depends only on \(x,y\).
\(s = g(x,y) = xy + y(9-x-y) + x(9-x-y) = 9y - y^2 + 9x - x^2 - xy\)
Find the critical points of \(g\).
\(\dfrac{\partial g}{\partial x} = 9 - 2x - y = 0 \implies 2x + y = 9\)
\(\dfrac{\partial g}{\partial y} = 9 - 2y - x = 0\)
Using the given constraint again, we have the condition
\(x+y+z = 2x+y \implies x=z\)
so that
\(x = 9 - x - y \implies y = 9 - 2x\)
and \(s\) depends only on \(x\).
\(s = h(x) = 9(9-2x) - (9-2x)^2 + 9x - x^2 - x(9-2x) = 18x - 3x^2\)
Find the critical points of \(h\).
\(\dfrac{dh}{dx} = 18 - 6x = 0 \implies x=3\)
It follows that \(y = 9-2\cdot3 = 3\) and \(z=3\), so the only critical point of \(s\) is at (3, 3, 3).
Differentiate \(h\) again and check the sign of the second derivative at the critical point.
\(\dfrac{d^2h}{dx^2} = -6 < 0\)
for all \(x\), which indicates a maximum.
We find that
\(\max\left\{xy+yz+xz \mid x+y+z=9\right\} = \boxed{27} \text{ at } (x,y,z) = (3,3,3)\)
The second derivative at the critical point exists
\($\frac{d^{2} h}{d x^{2}}=-6 < 0\) for all x, which suggests a maximum.
How to find the maximum value?Given, the constraint, we have
x + y + z = 9
⇒ z = 9 - x - y
Let s depend only on x, y.
s = g(x, y)
= xy + y(9 - x - y) + x(9 - x - y)
= 9y - y² + 9x - x² - xy
To estimate the critical points of g.
\($&\frac{\partial g}{\partial x}\) = 9 - 2x - y = 0
\($&\frac{\partial g}{\partial y}\) = 9 - 2y - x = 0
Utilizing the given constraint again,
x + y + z = 2x + y
⇒ x = z
x = 9 - x - y
⇒ y = 9 - 2x, and s depends only on x.
s = h(x) = 9(9 - 2x) - (9 - 2x)² + 9x - x² - x(9 - 2x) = 18x - 3x²
To estimate the critical points of h.
\($\frac{d h}{d x}=18-6 x=0\)
⇒ x = 3
It pursues that y = 9 - 2 \(*\) 3 = 3 and z = 3, so the only critical point of s exists at (3, 3, 3).
Differentiate h again and review the sign of the second derivative at the critical point.
\($\frac{d^{2} h}{d x^{2}}=-6 < 0\)
for all x, which suggests a maximum.
To learn more about constraint refer to:
https://brainly.com/question/24279865
#SPJ9
Write the subtraction expression as an equivalent addition expression and then evaluate it. 0−(−13)
Answers
Answer: 0+13, 13
Step-by-step explanation:0 minus negative 13 = 0 plus 13 = 13
Answer: 0 + 13
Step-by-step explanation:
This is what the problem means.
Whenever you try to subtract a negative number, it's like adding a positive number. So instead of 0-(-13), it would be 0 + 13.
There are no equal signs because it's an expression.
Please help me out, the question is in the image attached.
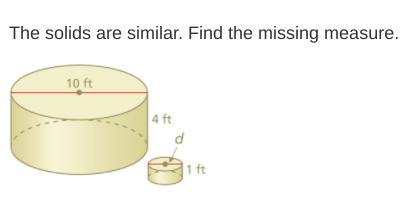
Answers
9514 1404 393
Answer:
d = 2.5 ft
Step-by-step explanation:
Similar figures have proportional linear measures.
diameter/height = d/1 = 10/4
d = 5/2 = 2.5 . . . . feet
Kiana wants to cover and area of her backyard with concrete patio stones in the shape of a right triangle each stone cost 0.42$ and covers 29.26 squares inches .Each square grid represents 1 square foot if R(1,1) E(7,9) and D(I5,3) what is the minimum number of stones Kiana should by to cover a right triangular area in her backyard show work below.Steps:1 what is the length of ER round your answer to the nearest tenth2. What is the length of ED leave your answer to the nearest tenth 3 what is the area of the triangle 4 what is the minimum number of stones required 5 what will the cost to the nearest dollar
Answers
The length of a segment with endpoints in (x1, y1) and (x2, y2) is calculated as:
\(\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}\)Then, the distance from E(7,9) to R(1,1) is:
\(\sqrt[]{(1-7)^2+(1-9)^2}=\sqrt[]{(-6)^2+(-8)^2}=\sqrt[]{100}=10\)At the same way, the distance from E(7,9) to D(15,3) is:
\(\sqrt[]{(15-7)^2+(3-9)^2}=\sqrt[]{8^2+(-6)^2}=\sqrt[]{100}=10\)Therefore ER has a length of 10 ft and ED has a length of 10 ft, So the area of the triangle is calculated as:
\(\text{Area}=\frac{ER\cdot ED}{2}=\frac{10\cdot10}{2}=50ft^2\)Because ER and ED are the base and the height of the right triangle
Now, we need to transform 50 square feet into square inches as:
\(50ft^2=50ft^2\cdot\frac{144in^2}{1ft^2}=7200in^2\)Now, the minimum number of stones required is calculated as:
\(\frac{7200in^2}{29.26in^2}=246.069\approx247\)Because every stone cover 29.26 square inches
Finally, the total cost of the stones is:
247 * $0.42 = $103.74
Because every stone has a cost of $0.42
Answers: 1. 10 ft
2. 10 ft
3. 50 ft^2 = 7200 in^2
4. 247
5. $103.74
Please help asap
The sales tax rate is 10%. If Carla buys a handbag priced at $90, how much tax will she
pay?
Answers
Answer: $9
Step-by-step explanation:
10 percent of 9 or 90 broken into 10 parts is 9 also 90 divided by 10 is 9
In the figure, AABC~ ADEF. If AP and DQ are altitudes, AP= 6, DQ = 10, and DE = 12, what is AB?
AB=
B
E
D
(Express your answer as a decimal.)
Answers
Answer:
If AP and DQ are altitudes, AP= 6, DQ = 10, and DE = 12, then AB = 8.
Step-by-step explanation:
(11/18-4/9)+1/6 pemdas fraction
Answers
Answer:
1/3
Step-by-step explanation:
11/18 - 4/9 + 1/6
= 1/6 + 1/6
= 1/3
The value of the fraction is 1/3.
What is PEMDAS Rule?PEMDAS rule is the same as BODMAS rule.
PEMDAS is the abbreviation for Parenthesis, Exponents, Multiplication, Division, Addition and Subtraction.
Given fraction is : (11/18 - 4/9) + 1/6
We have a parenthesis (brackets) in the given expression. First solve the operations inside the bracket.
And multiply the fraction 4/9 with 2 on both numerator and denominator.
(11/18 - 4/9) + 1/6 = (11/18 - 8/18) + 1/6
= 3/18 + 1/6
There is only an operation of addition left.
Multiplying both numerator and denominator of 1/6 with 3,
(11/18 - 4/9) + 1/6 = 3/18 + 3/18
= 6/18
= 1/3
Hence the value of the fractional expression given is 1/3.
Learn more about PEMDAS here :
https://brainly.com/question/29172059
#SPJ2
What is the value of y?

Answers
Answer:
C: 88
Step-by-step explanation:
There is a triangle that contains y, 53°, and 39°. So by this, you know that y + 53 + 39 = 180 (sum of triangle angles).
y = 180 - 53 - 39
y = 88°
Hope this helps! :)
An architect creates a blueprint using a scale of 1 inch = 3.5 ft. If the actual
length of a patio is 21 feet, how long will the patio's length appear in the
blueprint?
O 6 inches
O 7 inches
O 17.5 inches
O 73.5 inches
Answers
6 inches will be the length of the patio.
According to the scale, 1 inch on the plan corresponds to 3.5 feet in real life.
We must convert the patio's real length of 21 feet to inches using the scale in order to determine how long it would look on the blueprint:
3.5 feet to one inch
21 feet in x inches
If we cross-multiply, we obtain:
1 inch/3.5 feet * 21 feet
= x inches
= 6 inches.
As a result, the length of the patio will be indicated on the blueprint as 6 inches.
Learn more about scale here:
https://brainly.com/question/30468792
#SPJ1
Hi! Can someone help, please with a cherry on top?

Answers
Answer:
b bbb bbhdixbxidndidjd
Convert 506 minutes to hours and minutes.
Answers
Answer:
8 hours and 26 minutes
Step-by-step explanation:
To convert 506 minutes to hours and minutes, we can use the fact that there are 60 minutes in one hour.
First, we can divide 506 by 60 to find the number of hours:
506 ÷ 60 = 8 with a remainder of 26
This means that 506 minutes is equal to 8 hours and 26 minutes.
Therefore, the conversion of 506 minutes to hours and minutes is:
8 hours and 26 minutes
For each part, write the equation that represents the line in slope-intercept form (y = mx + b) and standard form (ax + by = c where a, b, and c are integers and a is not negative).

Answers
Answer:
The equation of a line is typically written as y=mx+b where m is the slope and b is the y-intercept
Step-by-step explanation:
Answer:
Step-by-step explanation:
slope-intercept equation for graph a: y = -x + 1
standard-form equation for graph a: x + y = 1
:::::
Slope of line through (0,-2) and (3,4) = (4-(-2))/(3-0) = 2
Slope-intercept equation for graph b: y = 2x-2
Standard form: 2x-y = 2
What is the standard form of y-7=-2(x+1)
Answers
it is math for evaluating functions please help

Answers
The domain of the given function is; (0, 2)
The range of the given function is; (-2, 6)
What is the range and domain of the given function?We want to evaluate the function f(x) = 4x - 2 for x = 0, 1 and 2.
Step 1;
f(0) = 4(0) - 2
f(1) = 4(1) - 2
f(2) = 4(2) - 2
Step 2;
f(0) = 0 - 2 = -2
f(1) = 4 - 2 = 2
f(2) = 8 - 2 = 6
The domain is the set of all possible input values which is (0, 2)
The range is the set of all possible output values which is (-2, 6)
Read more about range and domain at; https://brainly.com/question/2264373
#SPJ1