Use the contingency table to the right to determine the probability of events. a. What is the probability of event A? b. What is the probability of event A'? c. What is the probability of event A and B? d. What is the probability of event A or B? A A B 90 30 В' 60 70
Answers
The probability of event A' is 0.417
The probability of event A and B is 0.208
The probability of event A or B is 0.875
What is the probability of event A'?The contigency table is given as
B B'
A 50 90
A' 70 30
So, we have
P(A') = (70 + 30)/(50 + 90 + 70 + 30)
Evaluate
P(A') = 0.417
What is the probability of event A and B?From the table, we have
A and B = 50
So, we have
P(A and B) = (50)/(50 + 90 + 70 + 30)
Evaluate
P(A and B) = 0.208
What is the probability of event A or B?Here, we have
A or B = 50 + 90 + 50 + 70 - 50
A or B = 210
So, we have
P(A or B) = (210)/(50 + 90 + 70 + 30)
Evaluate
P(A or B) = 0.875
Read more about probability at
https://brainly.com/question/31649379
#SPJ4
Related Questions
A city planning commission recently voted to restrict the size of home remodels by limiting the floor area to lot area ratio to maximum of 0.60 to 1. Under these guidelines,
A) what would be the maximum allowable size of a remodel on an 11,400 sq ft lot?
B) what size lot would be required in order to create a 5040 sq ft remodel?
Answers
Answer:
Step-by-step explanation:
From the given information:
The ratio of the limiting floor area to lot area is 0.60 to 1
i.e.
= 0.60 : 1
For instance, let's take that the remodel size as p sq.ft on 1140 sq.ft
Then, the ratio = \(\dfrac{p}{11400}\)
The proportion of these equations is as follows:
\(\dfrac{p}{11400} = \dfrac{0.60}{1}\)
\(p \times 1 = 11400 \times 0.60\)
\(p = 11400 \times \dfrac{60}{100}\)
\(p =\dfrac{ 11400 \times 60}{100}\)
\(p =\dfrac{ 114 \times 100 \times 60}{100}\)
\(p = 114 \times 60\)
p = 6840 sq ft
Thus, the maximum allowable size of a remodeled house is 6840 sq.ft
b.
Recall that, the size of the home remodeled by limiting floor to lot area is
0.60:1
Then the proportion equation form is as follows:
\(\dfrac{0.60}{1}= \dfrac{5040}{x}\)
By cross multiplying
\(0.60 \times x = 5040 \times 1\)
\(x = \dfrac{5040 \times 1}{0.60 }\)
\(x = \dfrac{5040 \times 100}{60 }\)
\(x = \dfrac{84 \times 60 \times 100}{60 }\)
\(x =84 \times 100\)
x = 8400 sq.ft
Hence, the size of lot area is 8,400 sq.ft
4x + 7 = 6x + 4. what is this answer step by step?
Answers
\(4x+7=6x+4\\\\\implies 6x -4x = 7-4\\\\\implies 2x = 3\\\\\implies x =\dfrac 32\)
Answer:
x= 3/2
Step-by-step explanation:
4x+7=6x+4
Step 1: Subtract 6x from both sides.
4x+7−6x=6x+4−6x
−2x+7=4
Step 2: Subtract 7 from both sides.
−2x+7−7=4−7
−2x=−3
Step 3: Divide both sides by -2.
-2x=-3
-2 -2
=
3/2
The sum of the squares of the lengths of the legs of an isosceles triangle is equal to the square of the length of the hypotenuse
Answers
Answer:
Below.
Step-by-step explanation:
False for all isosceles triangles except:
This is only true for a 45-45-90 triangle.
Please hurry I will mark you brainliest
What is the equation of the line through the point (2, 3) with slope -2?
Answers
Answer:
y = -2x+7
Step-by-step explanation:
The slope intercept form of a line is
y = mx+b where m is the slope and b is the y intercept
y = -2x+b
Using the point
3 = -2(2)+b
3 = -4+b
3+4 = b
7=b
y = -2x+7
the half-life of radium-226 is 1600 years. suppose we have a 27-mg sample. (a) how much of the sample will remain after 4500 years? (round your answer to one decimal place.) mg (b) after how many years will only 15 mg of the sample remain? (round your answer to one decimal place.) yr
Answers
(a) After 4500 years, the sample will remain 3.9 mg.
(b) The sample will remain 15 mg after 1369 years.
The result is obtained by using the exponential decay equation.
What is the exponential decay equation?The exponential decay equation can be used to calculate radioactive decay for the activity, the nuclei, and also the mass. The exponential decay equation for the mass is
\(m = m_{o} e^{-\lambda t}\)
Where
m = the initial massm₀ = the remaining massλ = decay constant (0.693/T½)T½ = half-lifet = decay timeThe half-life of radium-226 is 1600 years and the mass of a sample is 27 mg.
(a) What is the remaining mass after 4500 years?
(b) What is the decay time if the remaining mass is 15 mg?
First, let's calculate the decay constant.
λ = 0.693/T½
λ = 0.693/1600
λ = 0,000433
After 4500 years, the remaining mass is
\(m = m_{o} e^{-\lambda t}\)
\(m = 27 e^{-0.000433 \times 4500}\)
m = 27 × 0.142
m = 3.8 mg
If the remaining mass is 15 mg, the decay time is
\(m = m_{o} e^{-\lambda t}\)
\(15 = 27 e^{-0.000433 t}\)
\(ln \frac{15}{27} = ln (e^{-0.000433 t})\)
\(ln \frac{15}{27} = -0.000433 t\)
-0.588 = - 0.000433t
t = 1357.9 years
Hence,
(a) After 4500 years, the sample will remain 3.9 mg.
(b) The sample will remain 15 mg after 1369 years.
Learn more about radioactive decay here:
brainly.com/question/9796067
#SPJ4
Real world linear equation
I just don’t know how to plug it in all the numbers are already there

Answers
Answer: 3 toys
Step-by-step explanation:
Equation: 60-5t=45
Solving: 5t=60-45
5t=15
t=3
A baseball player hits a home run over the left-field fence, which is 104 m from home plate. The ball is hit at a point 1.12m directly above home plate, with an initial velocity directed 32.5° above the horizontal. By what distance does the baseball clear the 3.00 m high fence, if it passes over it 3.10 s after being hit?
Answers
The baseball clears the 3.00 m high fence by a distance of 42.3 m. This can be calculated using the equations of projectile motion. The initial velocity of the baseball is 31.4 m/s, and it is launched at an angle of 32.5° above the horizontal. The time it takes the baseball to reach the fence is 3.10 s.
The horizontal distance traveled by the baseball in this time is 104 m. The vertical distance traveled by the baseball in this time is 3.10 m. Therefore, the baseball clears the fence by a distance of 104 m - 3.10 m - 3.00 m = 42.3 m.
The equations of projectile motion can be used to calculate the horizontal and vertical displacements of a projectile. The horizontal displacement of a projectile is given by the equation x = v0x * t, where v0x is the initial horizontal velocity of the projectile, and t is the time of flight. The vertical displacement of a projectile is given by the equation y = v0y * t - 1/2 * g * t^2, where v0y is the initial vertical velocity of the projectile, g is the acceleration due to gravity, and t is the time of flight.
In this case, the initial horizontal velocity of the baseball is v0x = v0 * cos(32.5°) = 31.4 m/s. The initial vertical velocity of the baseball is v0y = v0 * sin(32.5°) = 17.5 m/s. The time of flight of the baseball is t = 3.10 s.
The horizontal displacement of the baseball is x = v0x * t = 31.4 m/s * 3.10 s = 104 m. The vertical displacement of the baseball is y = v0y * t - 1/2 * g * t^2 = 17.5 m/s * 3.10 s - 1/2 * 9.8 m/s^2 * 3.10 s^2 = 3.10 m.
Therefore, the baseball clears the 3.00 m high fence by a distance of 104 m - 3.10 m - 3.00 m = 42.3 m.
To learn more about equation click here : brainly.com/question/29657983
#SPJ11
Determine dw/dt for the following equations.
w = z - sen(xy), x = t, y = ln t,z = eᵗ⁻¹
Answers
The expression for dw/dt is \(e^(^t^-^1^)\)- (ln t + 1)cos(t ln t).
How to find dw/dt?To find dw/dt, we need to use the chain rule of differentiation and differentiate each term with respect to t.
First, we can substitute the given expressions for x, y, and z into the expression for w:
w = z - sin(xy) = \(e^(^t^-^1^)\) - sin(t ln t)
Now we can differentiate w with respect to t using the chain rule:
dw/dt = d/dt(\(e^(^t^-^1^)\)) - d/dt(sin(t ln t))
To find d/dt(\(e^(^t^-^1^)\)), we can use the chain rule:
d/dt(\(e^(^t^-^1^)\)) = d/dt(\(e^u\)) where u = t-1
= d/dt(u) * d/du(\(e^u\)) = 1 *\(e^(^t^-^1^)\) = \(e^(^t^-^1^)\)
To find d/dt(sin(t ln t)), we can also use the chain rule:
d/dt(sin(t ln t)) = d/dt(sin(u)) where u = t ln t
= d/dt(u) * d/du(sin(u)) = (ln t + 1) * cos(t ln t)
Putting it all together, we have:
dw/dt = \(e^(^t^-^1^)\) - (ln t + 1)cos(t ln t)
Therefore, the expression for dw/dt is \(e^(^t^-^1^)\) - (ln t + 1)cos(t ln t).
Learn more about derivative
brainly.com/question/30365299
#SPJ11
a cube and a sphere both have volume 512 cubic units. which solid has a greater surface area? explain your reasoning.
Answers
If the cube and sphere both have volume as 512 cubic units, then the solid that has a greater surface area is Cube.
we first find the side length of the cube and the radius of the sphere.
The volume of the cube is 512 cubic units,
We have,
⇒ side³ = 512,
⇒ side = 8
So, the side length of the cube is 8 units.
Volume of sphere is also 512 cubic units,
We have,
⇒ (4/3)πr³ = 512,
On Simplifying,
We get,
⇒ r = 4.96 units.
So, radius of sphere is = 4.96 units.
Next we can find the surface area of each solid.
The surface-area of cube is = 6×(side)²,
⇒ 6(side²) = 6(8²) = 384 square units,
The surface area of the sphere is = 4πr²,
⇒ 4π(r²) = 4π(4.96²) ≈ 309 square units.
Therefore, the Cube has a greater surface area than the sphere.
Learn more about Surface Area here
https://brainly.com/question/21600799
#SPJ4
9. Which unit of measure would be appropriate for the volume of a cube with sides of 2 meters.
Answers
Answer:
The unit of measure appropriate is cubic metre or cubic meter (m³)
Step-by-step Explanation:
we know that
The volume of a cube is equal to
V = b^3
where b is the length side of the cube
In this problem we have
b = 2m
substitute in the formula of volume
V = 2^3
V = 8 m^3
therefore
The unit of measure appropriate is cubic metre (m³)
Bag A contains 10 marbles of which 2 are red and 8 are black. Bag B contains 12 marbles of which 4 are red and 8 are black. A ball is drawn at random from each bag.
a) Draw a probability tree diagram to show all the outcomes the experiment.
Answers
Answer: Ok, so the tree would start with the ten marbles going to 1 of the reds, 1 of the black , and get till you used up all the black, then do 2/10 and 8/10 to 12 and repeat the 1 part step, and then do 4/12 and 8/12 and add it all up and place the probability out of 22.
Step-by-step explanation:
Let a=(−3,5,−9) and b=(9,−5,1) be vectors.
(A) Find the scalar projection of b onto a.
Scalar Projection:
(B) Decompose the vector b into a component parallel to a and a component orthogonal to a.
Parallel component: ( , , )
Orthogonal Component: ( , , )
Answers
a. The scalar projection of b onto a is -6.50
b. the vector b into a component parallel to a and a component orthogonal to a. Parallel component: (-1.67, 2.77, -5.24) and Orthogonal Component [9, -5, 1]
(A) The scalar projection of b onto a is given by:
proj_a(b) = (b . a) / ||a||
where "·" denotes the dot product and "|| ||" denotes the norm (magnitude) of a.
So, we have:
b . a = (-3)(9) + (5)(-5) + (-9)(1) = -78
||a|| = √[(-3)^2 + 5^2 + (-9)^2] = √[115]
Therefore:
proj_a(b) = (-78) / √[115] ≈ -6.50
(B) To find the component of b parallel to a, we can use the scalar projection we just found and multiply it by the unit vector in the direction of a. The unit vector in the direction of a is given by:
u_a = a / ||a||
So, we have:
comp_parallel = proj_a(b) * u_a
= (-6.50) * [(-3)/sqrt[115], 5/√[115], (-9)/sqrt[115]]
≈ (-1.67, 2.77, -5.24)
To find the component of b orthogonal to a, we can subtract the parallel component from b:
comp_orthogonal = b - comp_parallel
= [9, -5, 1] - (-1.67, 2.77, -5.24)
≈ (10.67, -7.77, 6.24)
Learn more about Vectors here
brainly.com/question/17157663
#SPJ11
Please help!!
At first, there were 930 women and men at a funfair altogether. After 4/5
the women and 1/2
of the men had left, a total of 360 men and women
remained at the funfair. How many women were there at the funfair at first?
Answers
What trigonometric ratio is 6/10?

Answers
Answer:
tanC
Step-by-step explanation:
tanC = \(\frac{opposite}{adjacent}\) = \(\frac{AB}{BC}\) = \(\frac{6}{10}\)
Given are the following data for year 1: Profit after taxes = $5 million; Depreciation = $2 million; Investment in fixed assets = $4 million; Investment net working capital = $1 million. Calculate the free cash flow (FCF) for year 1:
Group of answer choices
$7 million.
$3 million.
$11 million.
$2 million.
Answers
The free cash flow (FCF) for year 1 can be calculated by subtracting the investment in fixed assets and the investment in net working capital from the profit after taxes and adding back the depreciation. In this case, the free cash flow for year 1 is $2 million
Free cash flow (FCF) is a measure of the cash generated by a company after accounting for its expenses and investments in fixed assets and working capital. It represents the amount of cash available to the company for distribution to its shareholders, reinvestment in the business, or debt reduction.
In this case, the given data states that the profit after taxes is $5 million, the depreciation is $2 million, the investment in fixed assets is $4 million, and the investment in net working capital is $1 million.
The free cash flow (FCF) for year 1 can be calculated as follows:
FCF = Profit after taxes + Depreciation - Investment in fixed assets - Investment in net working capital
FCF = $5 million + $2 million - $4 million - $1 million
FCF = $2 million
Therefore, the free cash flow for year 1 is $2 million. This means that after accounting for investments and expenses, the company has $2 million of cash available for other purposes such as expansion, dividends, or debt repayment.
Learn more about free cash flow here:
brainly.com/question/28591750
#SPJ11
Find x:
(Round the answer to the nearest tenth if there is a decimal)
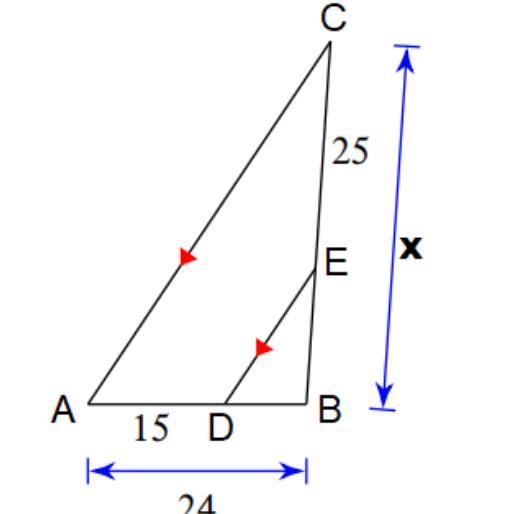
Answers
Answer:Angle x is congruent with the interior angle opposite side 8 (alternate interior angles)
Use tangent:
tan x = 8/15
x = arctan (8/15)
x = 28.1° (rounded)
Step-by-step explanation:
Perform the calculation and report your results to the correct number of significant figures. (10.52)(0.6721)
(19.09−15.347)
Answers
The results of the calculations are approximately 7.07 and 3.74, respectively, to the correct number of significant figures.
Performing the calculation:
(10.52)(0.6721) = 7.0671992
Rounding to the correct number of significant figures, we have:
(10.52)(0.6721) ≈ 7.07
Next, let's calculate (19.09 - 15.347):
(19.09 - 15.347) = 3.743
Rounding to the correct number of significant figures, we have:
(19.09 - 15.347) ≈ 3.74
Therefore, the results of the calculations are approximately 7.07 and 3.74, respectively, to the correct number of significant figures.
Learn more about significant figures here
https://brainly.com/question/30169
#SPJ11
One number is six times another number and their difference is thirty. Find the number
Answers
One number is six times another number and their difference is thirty. The smaller number is 6 and the larger number is 36.
Let x be the smaller number and y be the larger number.
According to the problem, y = 6x and y - x = 30. We can substitute the first equation into the second equation to get: 6x - x = 30
Simplifying, we get: 5x = 30
Dividing both sides by 5, we get: x = 6
Now that we know the value of x, we can substitute it into the first equation to find y: y = 6x = 6(6) = 36
Therefore, the smaller number is 6 and the larger number is 36.
Visit here to learn more about Equation:
brainly.com/question/29174899
#SPJ11
25x+5y=15
what would be the answer
Answers
Answer:
3-y/3
The slope is -2/5
Step-by-step explanation:

LAST ONE PLS HELP PLS ASAP PLS PLS HELP ASAP THANKS ILL GIVE BRAINLKEST PLS THANKS PLS

Answers
Answer:
1/5
Step-by-step explanation:
Total Frequency is 14+21+70 = 105
Sewing has frequency of 21
21/105 = 0.2 = 1/5
How long will it take l to catch up to c lauren can run 24 feet in 3 seconds clara can run 20 feet in 5 seconds clara has a 40 foot head start l will catch c in how many seconds after running how many feet
Answers
Answer:
They both will meet each other when they both have been running for 10 seconds
Lauren will run \(x=80\ \text{ft}\) and Clara will run \(40\ \text{ft}\)
Step-by-step explanation:
Velocity of Lauren
\(v_l=\dfrac{24}{3}\\\Rightarrow v_l=8\ \text{ft/s}\)
Velocity of Clara
\(v_c=\dfrac{20}{5}\\\Rightarrow v_c=4\ \text{ft/s}\)
Let distance traveled by Lauren be \(x\)
As Clara has a 40 feet head start distance she will travel is \(x-40\)
\(\text{Time}=\dfrac{\text{Distance}}{\text{Speed}}\)
The time that will have passed when they both will meet will be the same for both of them so
\(\dfrac{x-40}{4}=\dfrac{x}{8}\\\Rightarrow 8x-320=4x\\\Rightarrow 8x-4x=320\\\Rightarrow 4x=320\\\Rightarrow x=\dfrac{320}{4}\\\Rightarrow x=80\ \text{ft}\)
Time they will meet is \(\dfrac{80-40}{4}=\dfrac{80}{8}=10\ \text{s}\).
So, Lauren will run \(x=80\ \text{ft}\) and Clara will run \(x-40=80-40=40\ \text{ft}\).
Find the slope of the line.
y = 3/4x + 207
Answers
Remeber y = mx + c
You are playing cards. A standard deck is made up of cards from 4 suits (clubs, hearts, diamonds, and spades).What is the fewest number of cards that you need to draw so that you are certain that you have at least two cards of the same suit?235768
Answers
Given:
A standard deck is made up of cards from 4 suit clubs, hearts, diamonds, and spades.
Required:
Find the fewest number of cards that you need to draw so that you are certain that you have at least two cards of the same suit.
Explanation:
The total number of cards = 52
The number of cards with the same suit = 13
The probability of an event is given by the formula:
\(P=\frac{Number\text{ of possible outcomes}}{Total\text{ outcomes}}\)The probability of drawing two cards with the same suit is:
\(\begin{gathered} P=4\times\frac{13}{52}\times\frac{12}{51} \\ =\frac{4}{17} \end{gathered}\)Final Answer:
The probability of
What is ""statistical conclusion validity""? what was the main threat to statistical conclusion validity discussed in class?
Answers
Statistical conclusion validity is the extent to which inferences and conclusions drawn from statistical data are valid.
The main threat to statistical conclusion validity discussed in class is the potential for spurious correlations. This is when two variables appear to be related when in fact they are not.
Statistical conclusion validity is a measure of how valid the conclusions drawn from statistical data are. This is important because it allows us to draw valid inferences from the data. The main threat to statistical conclusion validity discussed in class is the potential for spurious correlations. This is when two variables appear to be related when in fact they are not. For example, a study may show that there is a correlation between ice cream sales and crime rate, when in fact it is merely a coincidence that both variables increase during the summer months. By controlling for other variables and using appropriate statistical tests, it is possible to identify and avoid spurious correlations.
Learn more about statistic here
https://brainly.com/question/14128303
#SPJ4
A particle moves on xy plane according to equations: x(t)=2t^3−3t;y(t)=t^2 +4 (Take g=10 m/s^2. Please mark the closest answer as correct answer ) Find the angle between acceleration and velocity vectors at t=1 a) 46,6°(b) 13.5°(c) 65,90 (d) 24.2^0
Answers
The angle between the acceleration and velocity vectors at t=1 is 46.6°. Hence the answer is (a) 46.6°.
To obtain the angle between the acceleration and velocity vectors at t=1, we need to differentiate the position equations to obtain the velocity and acceleration equations.
We have:
x(t) = 2t³ - 3t
y(t) = t² + 4
To calculate the velocity, we take the derivatives of x(t) and y(t) with respect to time (t):
\(\[ v_x(t) = \frac{d}{dt} \left(2t^3 - 3t\right) = 6t^2 - 3 \]\)
\(\[v_y(t) = \frac{{d}}{{dt}} \left(t^2 + 4\right) = 2t\]\)
So the velocity vector at any time t is: \(\[ v(t) = (v_x(t), v_y(t)) = (6t^2 - 3, 2t) \]\)
To calculate the acceleration, we differentiate the velocity equations:
\(\[a_x(t) = \frac{{d}}{{dt}} \left[6t^2 - 3\right] = 12t\]\)
\(\[a_y(t) = \frac{{d}}{{dt}} \left[2t\right] = 2\]\)
So the acceleration vector at any time t is: \(\[a(t) = (a_x(t), a_y(t)) = (12t, 2)\]\)
Now, we can calculate the acceleration and velocity vectors at t=1:
v(1) = (6(1)² - 3, 2(1)) = (3, 2)
a(1) = (12(1), 2) = (12, 2)
To obtain the angle between two vectors, we can use the dot product and the formula:
\(\[\theta = \arccos\left(\frac{{\mathbf{a} \cdot \mathbf{v}}}{{\|\mathbf{a}\| \cdot \|\mathbf{v}\|}}\right)\]\)
Let's calculate the angle:
\(\(|a| = \sqrt{{(12)^2 + 2^2}} = \sqrt{{144 + 4}} = \sqrt{{148}} \approx 12.166\)\\\(|v| = \sqrt{{3^2 + 2^2}} = \sqrt{{9 + 4}} = \sqrt{{13}} \approx 3.606\)\)
(a⋅v) = (12)(3) + (2)(2) = 36 + 4 = 40
\(\\\[\theta = \arccos\left[\frac{40}{12.166 \times 3.606}\right]\]\)
θ ≈ arccos(1.091)
Using a calculator, we obtain that the angle is approximately 46.6°.
Therefore, the closest answer is (a) 46.6°.
To know more about angle between two vectors refer here:
https://brainly.com/question/33440545#
#SPJ11
What is the length of the line?
A. 9
B. 8
C. squared 45
D. squared 27

Answers
one side is 3 units long, we’ll call it “a”.
the other side is 6 units long, “b”.
using a^2 +b^2=c^2
we can get 3^2+ 6^2 =c^2
9+36=c^2
45=c^2
square root of 45=c
the answer is C!
Answer:
C) \(\sf \sqrt{45}\)
Step-by-step explanation:
Pythagorean theorem:
AB = 6 units
BC = 3 units
AC is hypotenuse and AB is the base and BC is the altitude.
Hypotenuse² = base² + altitude²
AC² = AB² + BC²
\(\sf = 6^2 + 3^2\\\\ = 36 + 9\\\\ = 45\)
\(\sf AC= \sqrt{45}\)

what is the probability that each player has a hand con- taining an ace when the 52 cards of a standard deck are dealt to four players
Answers
The probability that each player has a 5-card hand an ace when the 52 cards is 5/13.
Given is 52 cards of a standard deck, we need to find the probability of picking an ace,
so,
There are 4 aces in the 52-card deck so the probability of dealing an ace is 4/52 = 1/13.
In a 5-card hand, each card is equally likely to be an ace with probability 1/13. So together, the expected number of aces in a 5-card hand is 5 * 1/13 = 5/13.
Hence the probability that each player has a 5-card hand an ace when the 52 cards is 5/13.
Learn more about probability click;
https://brainly.com/question/32117953
#SPJ1
solve this t/3 = 4/9
Answers
Sally's soccer team played 25 games and won 17 of them. What percent did the team win
Answers
Answer:
68%
Step-by-step explanation:
Answer:
Sally's soccer team won 68% of the games they played.
the slope of a steep upward-sloping line will be a
Answers
Main Answer: The slope of a steep upward-sloping line will be a positive.
Supporting Question and Answer:
How is the slope of a line calculated?
The slope of a line is calculated by dividing the change in the y-coordinate (vertical change) between any two points on the line by the change in the x-coordinate(horizontal change)between the same two points.This is represented by the formula:
slope= \(\frac{(y_2-y_1)}{(x_2-x_1)}\) ,where \((x_1,y_1)\) and \((x_2,y_2)\) are two points on the line.
Body of the Solution:In mathematics, the slope of a line is defined as the ratio of the change in the y-coordinate to the change in the x-coordinate between any two points on the line. A positive slope indicates that the line is increasing in the y-direction as the x-coordinate increases.
A steep upward-sloping line means that the line is increasing rapidly in the y-direction as the x-coordinate increases, and therefore the slope of the line will be a large positive number. Conversely, a steep downward-sloping line will have a large negative slope, indicating that the line is decreasing rapidly in the y-direction as the x-coordinate increases.
Therefore, the slope of a steep upward-sloping line will be a positive.
Final Answer:The slope of a steep upward-sloping line will be a positive.
To learn more about the slope of a line from the given link
https://brainly.com/question/16949303
#SPJ4