Vocabulary
Choose the best term from the box to complete each definition.
1. The number of square units that a figure covers is its
2. The
of a triangle is the length of the perpendicular
line segment from a vertex to the opposite side.
of a solid figure is the number of cubic units needed
3. The
to fill it.
4. Any line segment that connects the center of a circle to a point on the
circle is called a
area
base
diameter
height
radius
volume
Answers
The number of square units that a figure covers is its area.
The height of a triangle is the length of the perpendicular line segment from a vertex to the opposite side.
The volume of a solid figure is the number of cubic units needed to fill it.
Any line segment that connects the center of a circle to a point on the circle is called a radius.
The area of a figure refers to the number of square units that the figure covers.
It is a measure of the surface enclosed by the figure.
In the context of a triangle, the height refers to the length of the perpendicular line segment drawn from a vertex of the triangle to the opposite side or the line containing the opposite side.
The volume of a solid figure measures the amount of space occupied by the figure in three dimensions.
The radius of a circle is any line segment that connects the center of the circle to a point on the circle's circumference.
To learn more on Circles click:
https://brainly.com/question/11833983
#SPJ1
Related Questions
What is the slope of the line passing through the given points 4,2 and -2,1
Answers
Answer:
Alright, here is the formula.
m = (y2 -- y1) / (x2 -- x1)
So, now we have to take the points and replace them with the variables.
m = (1 - 2) / (-2 - 4)
Great! So now, we have to solve.
1 - 2 = -1
-2 - 4 = -6
So now, it would be:
-1/6
That is the slope! Hope this helps! :)
In this problem, you will investigate segments of circles. A segment of a circle is the region bounded by an arc and a chord.
b. Tabular Calculate and record in a table ten values of A for x -values ranging from 10 to 90 if r is 12 inches. Round to the nearest tenth.
Answers
Here is a table showing ten values of the segment area (A) for x-values ranging from 10 to 90, assuming the radius (r) is 12 inches. The values are rounded to the nearest tenth:
| x-value | Segment Area (A) |
|--------- |-----------------|
| 10 | 0.7 |
| 20 | 2.8 |
| 30 | 6.3 |
| 40 | 11.2 |
| 50 | 17.5 |
| 60 | 25.1 |
| 70 | 34.0 |
| 80 | 44.1 |
| 90 | 55.4 |
To calculate the segment area (A) of a circle for different x-values, we need to use the formula for the area of a segment: A = (1/2) * r^2 * (θ - sin(θ)), where r is the radius and θ is the central angle in radians. In this case, the radius is given as 12 inches. We can calculate the central angle θ using the relationship between x and θ, where θ = 2 * arccos((r - x) / r). By substituting the given radius and x-values into the formula, we can calculate the corresponding segment areas (A) rounded to the nearest tenth. This table provides the segment areas for x-values ranging from 10 to 90.
Learn more about circle here: brainly.com/question/12930236
#SPJ11
Help is appreicated! (10 points!)

Answers
Answer:
5
Step-by-step explanation:
5
ou have three submissions for each question except the multiple choice questions 4. [-15 Points ] Find the volume of the largest rectangular box in the first octant with three faces in the coordinate planes and one vertex in the plane x+y+z=3.
Answers
The volume of the largest rectangular box in the first octant with three faces in the coordinate planes and one vertex in the plane x + y + z = 3 is 27.
We can use the following steps to solve the given problem:
Step 1: Consider the given plane equation x + y + z = 3.
Step 2: Now, find the intercepts of the plane on the axes, as follows:Putting x = 0 and y = 0 in the equation x + y + z = 3, we get z = 3.So, the z-intercept is 3.Putting x = 0 and z = 0 in the equation x + y + z = 3, we get y = 3.So, the y-intercept is 3.Putting y = 0 and z = 0 in the equation x + y + z = 3, we get x = 3.So, the x-intercept is 3.Therefore, the intercepts of the plane x + y + z = 3 on the three axes are 3, 3, and 3.
Step 3: Let the rectangular box be of dimensions l, b, and h, respectively, and one of its vertices be (0, 0, 0).So, the other three vertices of the box will be (l, 0, 0), (0, b, 0), and (0, 0, h).Also, the coordinates of the vertex of the rectangular box on the plane x + y + z = 3 will be (3, 0, 0), (0, 3, 0), and (0, 0, 3).Hence, l = 3, b = 3, and h = 3.Substituting these values in the formula for the volume of a rectangular box, we get:V = l × b × h= 3 × 3 × 3= 27Therefore, the volume of the largest rectangular box in the first octant with three faces in the coordinate planes and one vertex in the plane x + y + z = 3 is 27.
To know more about coordinate planes :
https://brainly.com/question/28471473
#SPJ11
5+4+5+123456= ??
what is it and something to make your day. I psi = photoshopped it

Answers
Answer:
Step-by-step explanation:
12,359 lolll
Answer:
123470
easy question dude plz mark me as brainliest
what is the measure of angle 4? Pls i need help

Answers
Answer:
254
Step-by-step explanation:
the angle is 254
Find the volume of the solid lying under the circular paraboloid z = x2 + y2 and above the rectangle R = (-4,4] x [-6,6). 1. 2496 2. 1664 3. 1248 4. 960 5. 640
Answers
According to the question we have the correct answer is option 2, with a volume of 1664 cubic units.
The volume of the solid lying under the circular paraboloid z = x^2 + y^2 and above the rectangle R = (-4, 4] x [-6, 6] can be found using a double integral. First, set up the integral with respect to x and y over the given rectangular region:
Volume = ∬(x^2 + y^2) dA
To evaluate this integral, we will use the limits of integration for x from -4 to 4, and for y from -6 to 6:
Volume = ∫(from -4 to 4) ∫(from -6 to 6) (x^2 + y^2) dy dx
Now, integrate with respect to y:
Volume = ∫(from -4 to 4) [(y^3)/3 + y*(x^2)](from -6 to 6) dx
Evaluate the integral at the limits of integration for y:
Volume = ∫(from -4 to 4) [72 + 12x^2] dx
Next, integrate with respect to x:
Volume = [(4x^3)/3 + 4x*(72)](from -4 to 4)
Evaluate the integral at the limits of integration for x:
Volume = 1664
Therefore, the correct answer is option 2, with a volume of 1664 cubic units.
To know more about Volume visit :
https://brainly.com/question/28058531
#SPJ11
Select the correct answer. It takes greg and nikki a total of 40 minutes to paint a room if they work together. If greg works alone, he takes 18 minutes longer to paint he room than nikki takes if she works alone. When x represents the number of minutes it takes nikki to paint the room working alone, the situation is represented by this equation: which value is a solution of the rational equation that must be discarded because of the context? a. X = 0 b. X = -10 c. X = -18 d. X = -72.
Answers
Therefore, (b) x = -10 is the result that is a solution of the rational equation that must be ignored due to the context.
What is quadratic equation?Any equation in algebra that can be written in standard form as where x stands for an unknown value and a, b, and c stand for known values is said to be a quadratic equation. In general, it is assumed that a > 0; equations with a = 0 are regarded as degenerate since they become linear or even simpler. ax2 + bx + c = 0 is a quadratic equation, which is a second-order polynomial equation in a single variable. a 0. It has at least one solution since it is a second-order polynomial equation, which is guaranteed by the algebraic basic theorem. The answer could be simple or complicated.
Here,
1/x+1/(x+18)=1/40
x+18+x/x(x+18)=1/40
2x+18/x²+18x=1/40
40(2x+18)=x²+18x
80x+720=x²+18x
x²-62x-720=0
On solving the quadratic equation,
x=-10,72
So, the value that is a solution of the rational equation that must be discarded because of the context is (b) x = -10.
To know more about quadratic equation,
https://brainly.com/question/18943325
#SPJ4
Need help with this
“Use the law of Cosines to find the missing side length. Set up and SHOW YOUR WORK”
1: 38km
2:48km
3:41km
4:46km

Answers
Answer:
law of cosines states c^2=a^2+b^2-2abc
b^2=26^2+24^2-2(26×24)cos 134°
b^2=676+576-1248cos134°
cos134= -0.6946
b^2=1252-12(-0.6946)
12×(-0.6946)= -8.3352
b^2=1252-(-8.3352)
b^2=1252+8.3352
b^2=1260.33
b=√1260.33
b=35.50
Norma is buying a home with a $180,000 mortgage using a 5.5 percent, 30-year loan. How much of the first month's payment will go to principal
Answers
In the first month's payment for a $180,000 mortgage with a 5.5 percent, 30-year loan, a portion will go towards the principal. The exact amount can be determined using an amortization schedule.
To calculate how much of the first month's payment goes towards the principal, we can follow these steps:
Step 1: Determine the monthly interest rate: Divide the annual interest rate by 12 to obtain the monthly interest rate. In this case, 5.5 percent divided by 12 equals 0.004583 (approx).
Step 2: Calculate the monthly payment: Use a loan payment formula or a mortgage calculator to determine the monthly payment amount. For a $180,000 mortgage with a 30-year loan term and a 5.5 percent interest rate, the monthly payment would be approximately $1,019.32 (approx).
Step 3: Create an amortization schedule: An amortization schedule shows the breakdown of each monthly payment, indicating the amount allocated to interest and principal. Using the loan details, create an amortization schedule or use an online tool to generate one.
Step 4: Locate the first month on the schedule: Find the first month's entry on the amortization schedule to determine the amount allocated to principal. This amount will vary depending on the specific terms of the loan. Locate the principal portion of the payment, which represents the reduction of the loan balance.
By following these steps and referencing the amortization schedule, you can determine the exact amount of the first month's payment that goes towards the principal of the $180,000 mortgage.
Learn more about monthly interest rate here:
https://brainly.com/question/17293620
#SPJ11
If the _ of a parallelogram are perpendicular and a diagonal _opposite angles then the parallelogram is a _.
Answers
Simplify the expression. -5/8(-3/8-1/4)
Answers
Answer:
25/64
Step-by-step explanation:
To get this answer, first you need to use the distributive property:
(-3/8)(-5/8) - (1/4)(-5/8)
Next, multiply:
15/64 - (-5/32)
Change the negative signs into a positive sign:
15/64 + 5/32
Multiply 5/32 by 2 on both top and bottom:
15/64 + (5)(2)/(32)(2)
You will then get:
15/64 + 10/64
Now, add the numerators. You will get:
25/64
This is your answer. I hope it helped!
Please tell me what the Point Slope Slope Intercept Standard is for these graphs


Answers
Answer:
1st graph:
Slope-intercept is y = -7/2x + 3
Point Slope is y + 4 = -7/2(x - 2)
Standard is 7x + 2y = 6
2nd graph:
Slope-intercept is y = 1/2x - 4
Point Slope is y + 2 = 1/2(x - 4)
Standard is x - 2y = 8
3rd graph:
Slope-intercept is y = 3x - 3
Point Slope is y - 3 = 3(x - 2)
Standard is 3x - y = 3
4th graph:
Slope-intercept is y = -2/7x - 4
Point Slope is y + 2 = -2/7(x + 7)
Standard is 2x + 7y = - 28
Step-by-step explanation:
Point Slope formula⤵⤵⤵:
\(y - y _{1} = m(x - x _{1})\)
Slope-intercept formula⤵⤵⤵:
\(y = mx + b\)
Standard formula⤵⤵⤵:
\(Ax + By = C\)
Sorry this took a while, I was doing other stuff for school. I also had to relearn point slope for this, so it took me some time to figure it out. Hope this helps though :)
Which list shows the numbers in order from greatest to least?
A 4.232, 4.2, 4.142, 4.1
B 4.1, 4.142, 4.2, 4.232
C 4.232, 4.142, 4.2, 4.1
D 4.2, 4.232, 4.142, 4.1
Answers
Answer:
ignoring the decimal. The order from greatest to least is 2, 4, 5, 6, and 8
Solve for x.
144°
18 degrees
30 degrees
48 degrees
120 degrees
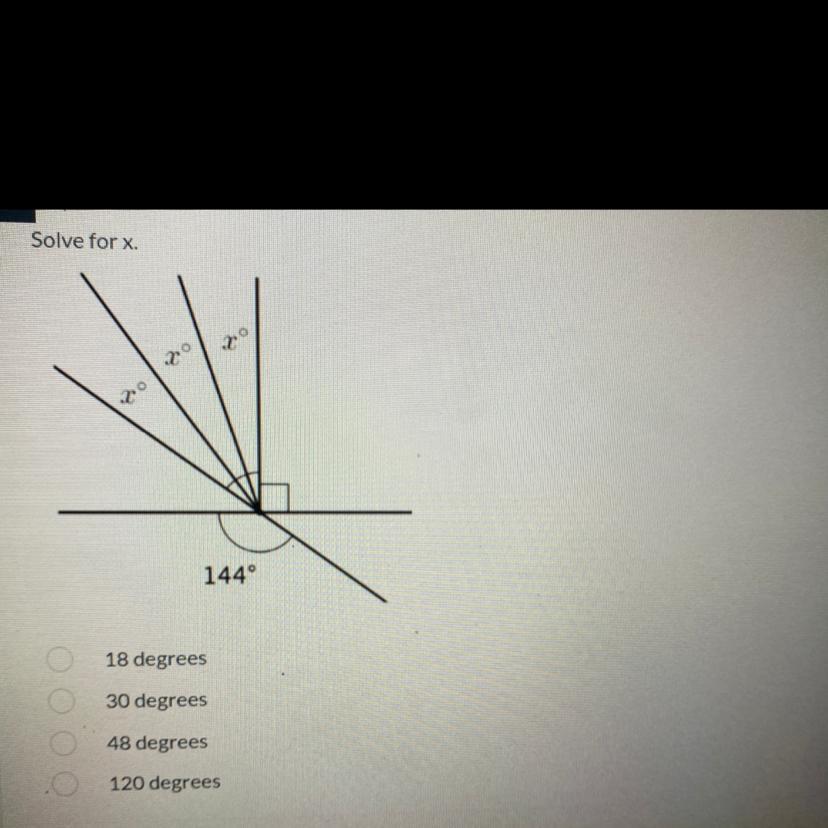
Answers
Answer:
x = 18 °Step-by-step explanation:
you have a rotation angle of 360 °, take out the known values (360 ° -90 ° -144 ° = 126), 144 ° is part of a flat angle of 180 °, from 180 ° remove 144 and you have 36 °, they are opposite angles therefore the same. therefore 360 - 144 - 90 - 36 - 36 = 54.
54 is 3x, so x = 18 ° (54 : 3 = 18)
Problem 2 A local girls soccer team decides to sell chocolate bars to raise some money for new uniforms. The girls are to receive 10% of all the sales they make. Once the bars arrive the girls see that they have to sell each bar for $2.50. They think this price is too high. Are the girls being altruistic or is there something else going on? (Assume the girls face a downward sloping demand curve).
Answers
The girls' reluctance to sell the chocolate bars at $2.50 per bar may not be purely altruistic but instead driven by their understanding of market demand and the potential impact of pricing on sales volume.
The girls' perception that the selling price of $2.50 per chocolate bar is too high may not necessarily indicate altruism but rather a response to market demand. When faced with a downward sloping demand curve, higher prices can lead to lower sales volume.
The girls' concern may be rooted in their understanding that a higher price could potentially deter potential buyers from purchasing the chocolate bars, resulting in lower overall sales and potentially lower earnings for themselves.
By considering the demand curve, the girls are likely taking into account the price elasticity of demand. Elastic demand implies that a change in price will have a relatively larger impact on the quantity demanded. If the girls perceive the demand for chocolate bars to be elastic, they might believe that a lower price would attract more customers and lead to increased sales volume.
Their concerns could also be motivated by their desire to achieve a balance between maximizing their sales and ensuring a reasonable profit margin. They might be aware that setting the price too high could lead to reduced demand and lower overall revenue, thereby limiting their earnings.
Learn more about volume here:
https://brainly.com/question/28058531
#SPJ11
HELP!!! WILL MARK BRAINIEST!!
1) midpoint of R(4,1) and (-1,6)
2) find the coordinate of the midpoint of the segment with the given endpoints; -3 and 8
3) find the midpoint; (-9,3) and (-3,4)
4) find the coordinates of the other endpoint of the segment given its midpoint and one endpoint, apply the midpoint formula and solve the two equations for x and y; midpoint (-9,-7), endpoint (-1,-12)
5) find the coordinates of the other endpoint of the segment given its midpoint and one endpoint, apply the midpoint formula and solve the two equations for x and y; midpoint (-11,-10) endpoint (-14,-13)
Answers
Answer:
1) ( \(-\frac{5}{2}\), \(\frac{5}{2}\))
2) 5
3) ( 2, \(\frac{1}{2}\))
4) (17, 2)
5) (8, 7)
Step-by-step explanation:
No. 1
You can use the midpoint formula: \(\frac{ChangeInX}{2} ,\frac{ChangeInY}{2}\)
So, the Change In X is: -1 - 4 = -5
And the Change in Y is: 6 - 1 = 5
Once you divide both of the changes by 2, you get
X: \(-\frac{5}{2}\)
Y: \(\frac{5}{2}\)
So the midpoint is: ( \(-\frac{5}{2}\), \(\frac{5}{2}\))
_________________________________________________________
No. 2
You can just find the middle of the two numbers. You could honestly just count it on your fingers if you wanted.
8 - 3 = 5
__________________________________________________________
No. 3
You can use the midpoint formula: \(\frac{ChangeInX}{2} ,\frac{ChangeInY}{2}\)
So, the Change In X is: -3 - (-9) = 6
And the Change in Y is: 4 - 3 = 1
Once you divide both of the changes by 2, you get
X: 2
Y: \(\frac{1}{2}\)
So the midpoint is: ( 2, \(\frac{1}{2}\))
__________________________________________________________
No. 4
You can use the midpoint formula: \(\frac{ChangeInX}{2} ,\frac{ChangeInY}{2}\)
So, the Change in X is: -1 - X
And the Change in Y is: -12 - Y
Once you divide both of the changes by 2, you get
X: \(\frac{-1-X}{2} = -9\)
-1 - X = -18
-X = -17
X = 17
Y: \(\frac{-12-Y}{2} = -7\)
-12 - Y = -14
-Y = -2
Y = 2
So the endpoint is: (17, 2)
__________________________________________________________
No. 5
You can use the midpoint formula: \(\frac{ChangeInX}{2} ,\frac{ChangeInY}{2}\)
So, the Change in X is: -14 - X
And the Change in Y is: -13 - Y
Once you divide both of the changes by 2, you get
X: \(\frac{-14-X}{2}=-11\)
-14 - X = -22
-X = -8
X = 8
Y: \(\frac{-13-Y}{2} =-10\)
-13 - Y = -20
-Y = -7
Y = 7
So the endpoint is: (8, 7)
In the equation 4 x 4 = 16, 4 is a
Answers
Answer:
Is a natural Number
Step-by-step explanation:
Answer:
Is a Factor
Step-by-step explanation:
Suppose you sample one value from a uniform distribution with a = 0 and b= 10. a. What is the probability that the value will be between 7 and 9? b. What is the probability that the value will be between 1 and 4? c. What is the mean? d. What is the standard deviation? a. The probability that the value will be between 7 and 9 is (Type an integer or a decimal.) b. The probability that the value will be between 1 and 4 is (Type an integer or a decimal.) c. The mean of the given uniform distribution is u (Type an integer or a decimal.) d. The standard deviation of the given uniform distribution is a (Round to four decimal places as needed.)
Answers
a) The probability that the value will be between 7 and 9 is 0.2. b) The probability that the value will be between 1 and 4 is 0.3. c) The mean of the uniform distribution is 5. d) The standard deviation of the given uniform distribution is approximately 2.8868.
To compute this problem, we'll use the properties of a uniform distribution.
a) The probability that the value will be between 7 and 9 can be calculated by finding the proportion of the interval [7, 9] relative to the total interval [0, 10]. Since the distribution is uniform, the probability is equal to the width of the interval [7, 9] divided by the width of the total interval [0, 10]:
Probability = (9 - 7) / (10 - 0) = 2 / 10 = 0.2
Therefore, the probability that the value will be between 7 and 9 is 0.2.
b) Similarly, the probability that the value will be between 1 and 4 is:
Probability = (4 - 1) / (10 - 0) = 3 / 10 = 0.3
Therefore, the probability that the value will be between 1 and 4 is 0.3.
c) The mean (u) of a uniform distribution can be calculated as the average of the minimum value (a) and the maximum value (b):
Mean (u) = (a + b) / 2 = (0 + 10) / 2 = 10 / 2 = 5
Therefore, the mean of the given uniform distribution is 5.
d) The standard deviation (σ) of a uniform distribution can be calculated using the following formula:
Standard deviation (σ) = (b - a) / √12
Standard deviation (σ) = (10 - 0) / √12 = 10 / √12 ≈ 2.8868 (rounded to four decimal places)
Therefore, the standard deviation of the uniform distribution is approximately 2.8868.
To know more about uniform distribution refer here:
https://brainly.com/question/30639872#
#SPJ11
Help me out with this question!! 50 points

Answers
C
The mistake the arrangers made is in the second inequality. They considered the number of caps to be bought should be at least 5 times greater than the number of blouses, not the other way around. The correct inequality should be C
The correct answer is D) The first inequality should be s + h ≤ 1800.
The organizers made an error in the first inequality. The given inequality 10s + 8h ≤ 1800 represents the total cost of buying shirts (10s) and hats (8h) should be less than or equal to $1800. However, this does not take into account the fact that the organizers want to buy at least 5 times as many shirts as hats, as indicated by the second inequality h ≥ 5s.
The correct way to represent this constraint is by using the equation s + h ≤ 1800, which ensures that the total number of shirts and hats purchased does not exceed $1800 in cost. This is because the organizers want to make sure that the total cost of shirts and hats combined does not exceed the budget of $1800.
what are differences or similarities between everyday logic and mathematical logic?
Answers
The main difference between everyday logic and mathematical logic is that everyday logic is based on general observations and opinions, while mathematical logic is based on precise statements and facts.
Differences:
- Everyday logic is based on common sense and intuition, while mathematical logic is based on strict rules and formulas.
- Everyday logic is often used to make decisions or solve problems in daily life, while mathematical logic is used to solve complex mathematical problems.
- Everyday logic can be subjective and influenced by personal beliefs or experiences, while mathematical logic is objective and follows a set of universally accepted principles.
Similarities:
- Both everyday logic and mathematical logic use reasoning to draw conclusions.
- Both everyday logic and mathematical logic rely on evidence and facts to support their conclusions.
- Both everyday logic and mathematical logic can be used to solve problems and make decisions.
In conclusion, while everyday logic and mathematical logic have some similarities in terms of their use of reasoning and evidence, they differ in their approach and application. Everyday logic is based on common sense and intuition, while mathematical logic is based on strict rules and formulas.
Know more about mathematical logic here:
https://brainly.com/question/28052598
#SPJ11
What is the value of the expression r + 1,988 if r = 2,976?
Answers
Answer:
r=988
Step-by-step explanation:
r=988
Answer:
4,964
Step-by-step explanation:
if r= 2,975 and since you have to add r+1,988 the you add 2,975+1,988 that equals:4,964.
If the mean of a normal distribution is 20 and its standard deviation is 3, between which values would 99.5 percent of the data observations be expected to fall?
Answers
99.5% of the data observations should fall between 11.579 and 28.421 according to expectations for the given normal distribution.
What is a normal distribution?
A continuous probability distribution for just a real-valued random variable in statistics is known as a normal distribution or Gaussian distribution.
According to the question, if the lower limit is a and the upper limit is b, then 99.5 percent of values fall between a and b.
part of values below a certain threshold, a= (1-0.995)/2 = 0.0025
Mean,m =20
Standard deviation,s = 3
Z = (X – m) / s
P(x<Z): 0.0025
P(x<Z) = 0.0025 can be determined for Z score.
according to the usual table, Z = -2.807
X = Zs+m
(-2.807 * 3) +20= 11.579
Lower limit = 11.579
Part of values that are less than b is equal to 0.995 + 0.0025 = 0.9975.
P(x<Z): 0.9975
Z score for which P(x<Z) = 0.9975 can be found
from the normal table as, Z = 2.807
X = Zs+m
(2.807 * 3) +20= 28.421
Upper limit = 28.421
99.5% of the data observations should fall between 11.579 and 28.421 according to expectations for the given normal distribution.
To learn more about normal distribution visit:
https://brainly.com/question/4079902
#SPJ1
A corporation earned a profit of $ 2.5 × 1 0 4 $2.5×10 4 for 200 days in a row. What was the corporation’s total profit during this time period? Express your answer in scientific notation.
Answers
Answer: hopefully the image helps
Step-by-step explanation:

Assuming that all years have 365 days and all birthdays occur with equal probability, how large must n be so that in any randomly chosen group of n people, the probability that two or more have the same birthday is at least 1/2?
Answers
it is seen that if the number of people in the group is n = 23, the probability that at least two people will have the same birthday is at least 1/2.
Let P(A) be the probability that in a randomly selected group of n people, at least two people have the same birthday.
If we assume that the year has 365 days, then the number of ways to select n people with different birthdays is n x (n-1) x (n-2) x ... x (n-364).
the probability of selecting n people with different birthdays is P(A') = n(n - 1)(n - 2)...(n - 364)/365nThen, the probability that at least two people in a group of n have the same birthday is given by P(A) = 1 - P(A').
We need to find the smallest value of n such that P(A) ≥ 1/2.Let's solve for this.Let us find n such that P(A) ≥ 1/2.
By using the complement rule, 1-P(A') = P(A).Then:1 - n(n - 1)(n - 2)...(n - 364)/365n ≥ 1/2n(n - 1)(n - 2)...(n - 364)/365n ≤ 1/2(2)n(n - 1)(n - 2)...(n - 364) ≤ 365n/2Now, take the natural logarithm of both sides and simplify as follows:ln[n(n - 1)(n - 2)...(n - 364)] ≤ ln[365n/2]nln(n) - ln[(n - 1)!] - ln[(n - 2)!] - ... - ln[2!] - ln[1!] ≤ ln[365n/2]
Therefore, we need at least 23 people in the group for the probability of two or more people having the same birthday to be at least 1/2.
This is because n = 23 is the smallest number for which the inequality holds, and therefore, it is the smallest number of people required to ensure that the probability of two or more people having the same birthday is at least 1/2.
To know more about number visit:
brainly.com/question/3589540
#SPJ11
Given: 4ABC, and BP is parallel to AC.
Prove: m21 + m22 + m23 = 180
Answers
Mathematical proofs are used to prove or disprove mathematical statements.
Mathematical theoremsThe theorems to use are:
The sum of angles on a straight line is 180 degreesAlternate angles are congruentThe proofFrom the question, we have: \(\triangle ABC\)
This means that, ABC is a triangle
Also, we have:
BP || AC
This means that lines BP and AC are parallel
So, the following angles are congruent by alternate angle theorem
\(\angle 5 \cong \angle 3\).\(\angle 4 \cong \angle 2\)The angles on a straight line add up to 180 degrees.
So, we have:
\(\angle 4 + \angle 1 + \angle 5 = 180\)
By substitution, the above equation becomes
\(\angle 2 + \angle 1 + \angle 3 = 180\)
Rewrite the equation as:
\(\angle 1 + \angle 2 + \angle 3 = 180\)
Hence, the statement that \(\angle 1 + \angle 2 + \angle 3 = 180\) has been proved
Read more about mathematical proofs at:
https://brainly.com/question/25296908
5.
a) A builder planned to build houses. Each
house will be built on
of an acre. How
much land would be needed for houses?
Show your work.
Divide
b) The builder began with 10 acres of land.
After houses were built, how much land
was left unused?
(No links No files help asap)
Answers
Answer:
For 7 houses you will need 5.83 acres of land and the builder will have 4.16 acres of land unused
Step-by-step explanation:
please help me I'll give brainliest

Answers
Answer: The last choice is correct \(\frac{9}{\sin\left(60\right)}\)
Step-by-step explanation: The information given in the diagram: AB is the hypotenuse of a right triangle, and the side opposite the 60° angle is 9 feet. you can use sine = 0pposite/Hypotenuse
You can find the sine of 60° which is the value of the ratio of the opposite side to the (unknown) hypotenuse. sin 60° = 0.866
You can set up the equation on a scientific calculator as \(\frac{9}{\sin\left(60\right)}\) but to see the logic use the value 0.866 = 9/h
reorganize to solve for h: divide both sides by 0.866 and multiply both by h to get
h = 9/0.866 solving that you get the length of AB
h = 10.393, which, rounded, is a logical length for the brace on the gate:
10.4 feet
A factory has a machine that packs product into boxes. The number of boxes it can pack in a
certain amount of time is shown on this table.
Based on the table,which statement is true?
A.the machine can pack 50 boxes in 99 minutes
B.the machine can pack 45 boxes in 88 minutes
C.the machine can pack 40 boxes in 66 minutes
D. The machine can pack 35 boxes In 77 minutes

Answers
Answer:
99
Step-by-step explanation:
let me know if im wrong
Calls for a particular center occur at an average rate of 30 per hour. Find the probability that there are at least two calls in a given minute, correct to 2 decimal places.
Answers
SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Get the probability of calls within a minute
\(\begin{gathered} 30\text{ calls = 1 hour} \\ 30\text{ calls = 60 minutes} \\ \text{Converting to calls per minute will be:} \\ \frac{30}{60}=0.5 \end{gathered}\)STEP 2: Write the formula for getting the probability that there are at least two calls in a given minute.
\(At\text{ least 2=}P(X\ge2)=1-(P(X=0)+P(X=1))\)STEP 3: Write the formula for P(X=r)
\(P(X=r)=\frac{e^{-np}\times(np)^r}{r!}\)STEP 4: Find P(X=0)
\(\begin{gathered} P(X=r)=\frac{e^{-np}\times(np)^r}{r!} \\ P(X=0)=\frac{e^{-0.5}\times(0.5)^0}{0!}=e^{-0.5}=0.6065 \end{gathered}\)STEP 5: Find P(X=1)
\(\begin{gathered} P(X=r)=\frac{e^{-np}\times(np)^r}{r!} \\ P(X=1)=\frac{e^{-0.5}\times(0.5)^1}{1!}=0.3033 \end{gathered}\)STEP 6: Find P(X>=2)
\(\begin{gathered} P(X\ge2)=1-(0.6065+0.3033) \\ P(X\ge2)=1-0.9098=0.0902 \end{gathered}\)Hence, the probability that there are at least two calls in a given minute is 0.0902