Answers
Answer:
woah this is cool! thanks! :)))
Step-by-step explanation:
Related Questions
Find a differential equation whose general solution is. y = C1e5t + C2e−6t. (Use yp for y' and ypp for y''.) Expert Answer. Who are the experts?
Answers
The differential equation corresponding to the given general solution y = C1e5t + C2e−6t is dependent on the specific values of b and c, which are yet to be determined.
The experts referred to in the question are typically professionals with expertise and knowledge in a specific field. In this case, the expert answer is expected to provide a differential equation whose general solution is given as y = C1e5t + C2e−6t.
To find the differential equation corresponding to the given general solution, we can differentiate the solution multiple times and then solve for the unknown coefficients. Let's proceed step by step:
Given general solution: y = C1e5t + C2e−6t
First, we differentiate y with respect to t:
y' = C1(5e5t) + C2(-6e−6t) = 5C1e5t - 6C2e−6t
Now, we differentiate y' with respect to t to find y'':
y'' = (d/dt)(5C1e5t) - (d/dt)(6C2e−6t) = 25C1e5t + 36C2e−6t
We now have the second derivative of y, which is y'':
y'' = 25C1e5t + 36C2e−6t
To find the corresponding differential equation, we equate y'' to an expression involving y and its derivatives. Let's assume the differential equation is of the form:
ay'' + by' + cy = 0
Substituting the values of y'' and y into the differential equation, we get:
25C1e5t + 36C2e−6t + b(5C1e5t - 6C2e−6t) + c(C1e5t + C2e−6t) = 0
Simplifying this equation, we obtain:
(25C1 + 5bC1 + cC1)e5t + (36C2 - 6bC2 + cC2)e−6t = 0
Since this equation must hold for all values of t, the coefficients of the exponential terms must be zero. Therefore, we have the following system of equations:
25C1 + 5bC1 + cC1 = 0 (1)
36C2 - 6bC2 + cC2 = 0 (2)
To determine the values of b and c, we need additional information or constraints. Without specific constraints, we cannot uniquely determine the values of b and c.
Therefore, the differential equation corresponding to the given general solution y = C1e5t + C2e−6t is dependent on the specific values of b and c, which are yet to be determined. The experts in the field, such as mathematicians or scientists specializing in differential equations, can provide further insights and techniques to solve differential equations based on specific constraints or boundary conditions.
Learn more about differential equation here
https://brainly.com/question/28099315
#SPJ11
Qd=95−4P
Qs=5+P
a. What is Qd if P=5 ? b. What is P if Qs=20 ? β=9 c. If Qd=Qs, solve for P.
Answers
P = 90 is the solution for the given equation.
Given: Qd=95−4
PQs=5+P
To find Qd if P=5:
Put P = 5 in the equation
Qd=95−4P
Qd = 95 - 4 x 5
Qd = 75
So, Qd = 75.
To find P if Qs = 20:
Put Qs = 20 in the equation
Qs = 5 + PP
= Qs - 5P
= 20 - 5P
= 15
So, P = 15.
To solve Qd=Qs, substitute Qd and Qs with their respective values.
Qd = Qs
95 - 4P = 5 + P
Subtract P from both sides.
95 - 4P - P = 5
Add 4P to both sides.
95 - P = 5
Subtract 95 from both sides.
- P = - 90
Divide both sides by - 1.
P = 90
Thus, P = 90 is the solution for the given equation.
To know more about substitute visit
https://brainly.com/question/29383142
#SPJ11
answerrrrrr plssss ill giveee brainliesttttt

Answers
\(m\angle E=\sin \dfrac{\sqrt{10}}{2\sqrt5}=\sin \dfrac{\sqrt2}{2}=45^{\circ}\)
A geologist gathered data about the total shoreline and maximum depth of several area lakes and organized the data into this table.
Total Shoreline (miles) 22 17 10 23 12 35 7
Maximum Depth (feet) 101 85 59 113 64 158 33
She then used a graphing tool to display the data in a scatter plot, with x representing the total miles of shoreline and y representing the maximum depth. She also used the graphing tool to find the equation of the line of best fit:
y = 4.26x + 10.908.
Based on the line of best fit, what is the approximate maximum depth of a lake that has 31 miles of shoreline?
Answers
Based on the line of best fit, the approximate maximum depth of a lake that has 31 miles of shoreline is; 142.968 ft
How to interpret a Line of best fit?The line of best fit is defined as a straight line which is drawn to pass through a set of plotted data points to give the best and most approximate relationship that exists between such data points.
Now, we are given a table of values that shows the total shoreline in miles which will be represented on the x-axis and then the maximum depth of several area lakes which will be represented on the y-axis.
However, when the geologist found the graph, she arrived at an equation of best fit as;
y = 4.26x + 10.908.
Thus, for 31 miles of shoreline, the approximate maximum depth is;
Approximate maximum depth = 4.26(31) + 10.908.
Approximate maximum depth = 142.968 ft
Read more about Line of best fit at; https://brainly.com/question/1441182
#SPJ1
Answer:
143 feet
Step-by-step explanation:
its technically 142 and change but edmentum rounds up
What value of x will make a0nm similar to ASRQ by the SAS similarity theorem?.
Answers
The value of x is 25 will make ΔONM similar to ΔSRQ by the SAS similarity theorem.
Given:
∠ONM is similar to ∠SRQ
From the figure
NM = 10
SR = 20
NO = 8
QR = x
SAS Similarity Theorem:
if two sides in one triangle are proportional to two sides in another triangle and the included angle in both are congruent, then the two triangles are similar.
Both the triangles are similar by SAS if
NO/NM = SR/QR
Now substitute the values
8/10 = 20/x
cross multiplication
8x = 200
dividing both sides by 8
x = 25
Learn more about the triangle here:
https://brainly.com/question/2773823
#SPJ4

The extent to which conclusions developed from data collected from a sample can be extended to the population is known as
Answers
The extent to which conclusions developed from data collected from a sample can be extended to the population is known as generalizability.
Generalizability is defined as the ability to extend the findings of a research study conducted on a sample to the population as a whole. The extent to which the research findings can be applied to other individuals, groups, or settings is determined by generalizability. The more representative the sample is of the population, the more generalizable the results will be to the population. However, if the sample is not representative of the population, the results may not be generalizable to the population as a whole. Therefore, it is important to ensure that the sample is representative of the population and that the study is conducted in a manner that minimizes bias and maximizes the validity of the results.
Learn more about generalizability:
brainly.com/question/30438587
#SPJ11
Pls help me calculate the total area of compound shapes?!?!?

Answers
Answer:
Left: 42ft^2
Right: 21ft^2
Step-by-step explanation:
Its the same question as last time.
Left: (3*10) + (2*6) = 42
Right: (3*5) + (2*3) = 21
The graph of h(x)=|x-10|+6 is shown on whitch interval is the graph increasing

Answers
what is 4547.14 in standard form
Answers
Answer:
4.54714 × 103
Step-by-step explanation:
A Square garden is 25m long
find its perimeter
Answers
If a triangle has lengths of 3ft and 54ft, what are all the possible lengths for the third side?
51ft
53ft
55ft
57ft
58ft
Answers
Answer:
53, 55
Step-by-step explanation:
by the triangular inequality theorem, in a triangle.. sum of two sides is always greater than the third side.
3+54=57 ... exclude 57 and 58
3+51=54 ... exclude 51
A supermarket gives a special
offer to cus-
tomers who purchase at least a pack of
vests and a pack of T-shirts. The offer is
restricted to a total of 7 of these items.
a) Write down three inequalities which
must be satisfied.
(b) Draw the graphs of the above condi-
tions and shade the region that satis-
fies them.
(c) If the supermarket makes a gain of N5
on each vest and N8 on each T-shirt,
find the maximum gain made by the
supermarket.
Answers
A) the three inequalities that must be satisfied are:
The number of vests, represented by x, must be a non-negative integer: x ≥ 0.The number of T-shirts, represented by y, must also be a non-negative integer: y ≥ 0.The total number of vests and T-shirts must not exceed 7: x + y ≤ 7.B) Graph shaded and satisfying all conditions is attached.
What is an inequality?An inequality in mathematics is a relationship that makes a non-equal comparison between two integers or other mathematical expressions.
It is most commonly used to compare the sizes of two numbers on a number line.
Learn more about Inequality:
https://brainly.com/question/29773201
#SPJ1

let f and g be the functions defined by f(x)=e^x and g(x)=x^4
Answers
The derivatives of f(x) and g(x) are f'(x) = e^x and g'(x) = 4x^3. The functions f(x) = e^x and g(x) = x^4 are given. We can find the values of f and g at specific points and calculate their derivatives to gain further insight into their behavior.
For f(x) = e^x, the function represents exponential growth. The value of f(x) increases rapidly as x increases. For example, when x = 0, f(0) = e^0 = 1. As x increases, the value of f(x) grows exponentially. The derivative of f(x) is f'(x) = e^x, which means the rate of change of f(x) at any point is equal to its current value.
For g(x) = x^4, the function represents a power function with even exponent. The value of g(x) increases as x increases, but at a slower rate compared to f(x). For example, when x = 0, g(0) = 0^4 = 0. As x increases, the value of g(x) increases, but not as rapidly as f(x). The derivative of g(x) is g'(x) = 4x^3, which means the rate of change of g(x) at any point is given by 4 times the cube of x.
In summary, f(x) = e^x represents exponential growth, where the value increases rapidly as x increases. g(x) = x^4 represents a power function, where the value increases but at a slower rate compared to f(x). The derivatives of f(x) and g(x) are f'(x) = e^x and g'(x) = 4x^3, respectively, providing information about their rates of change at any given point.
Learn more about derivation here:
https://brainly.com/question/27986273
#SPJ11
b) y and z are whole numbers.
y < 70
Z <= 60
Work out the largest possible value of y + z
Answers
The largest possible value of y+z will be "129".
The given whole numbers are:
\(y<70\)\(z \leq 60\)According to the question, the exact whole numbers will be:
The maximum possible value,
→ \(y = 69\)
The maximum possible value,
→ \(z = 60\)
hence,
The largest possible value will be:
= \(y+z\)
By substituting the values, we get
= \(69+60\)
= \(129\)
Thus the above solution is correct.
Learn more:
https://brainly.com/question/16763451
what is 47.7273 rounded
Answers
Answer: 48
Step-by-step explanation:
The 7 in the 10s place is higher than 4 so it brings the digit to the left one higher turning 47 to 48
2. How many bits are needed to represent decimal values ranging from 0 to 12,500?
Answers
To represent decimal values ranging from 0 to 12,500, we need 14 bits.
To determine the number of bits needed to represent decimal values ranging from 0 to 12,500, we need to find the smallest number of bits that can represent the largest value in this range, which is 12,500.
The binary representation of a decimal number requires log base 2 of the decimal number of bits. In this case, we can calculate log base 2 of 12,500 to find the minimum number of bits needed.
log2(12,500) ≈ 13.60
Since we can't have a fraction of a bit, we round up to the nearest whole number. Therefore, we need at least 14 bits to represent values ranging from 0 to 12,500.
Using 14 bits, we can represent decimal values from 0 to (2^14 - 1), which is 0 to 16,383. This range covers the values 0 to 12,500, fulfilling the requirement.
Learn more about whole number
brainly.com/question/29766862
#SPJ11
I got this question wrong. My teacher said something about altitude, but I have not a clue how to do it
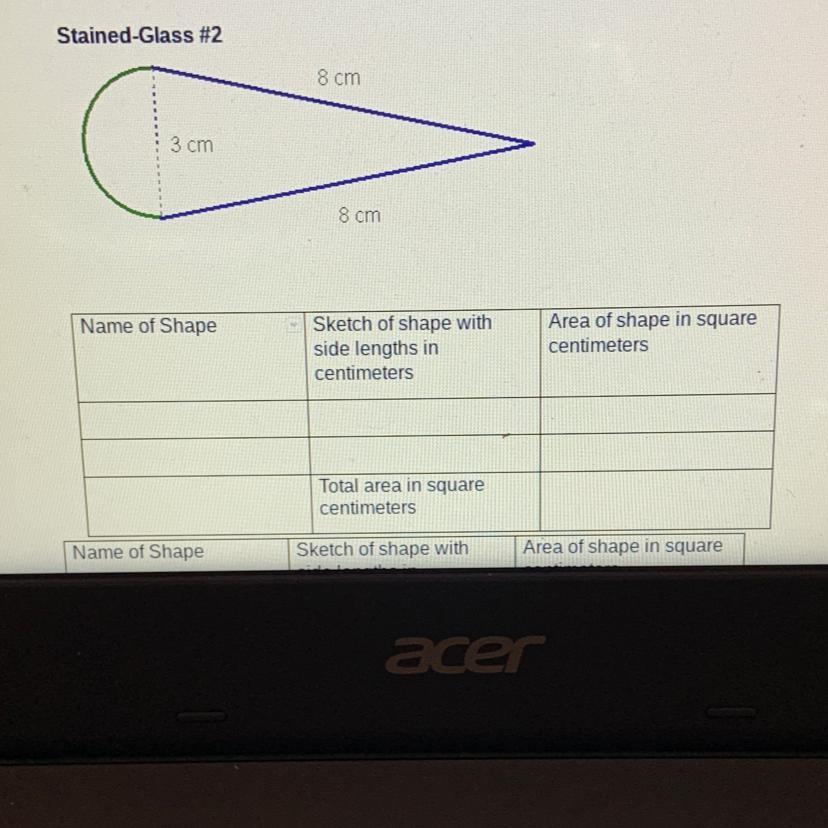
Answers
Answer:
cone shape and cm 3
area of shape
Step-by-step explanation:
3 cm ×8 cm
24
please follow me all friends who are watching me who made answer
What is the probability of NOT drawing a face card from a standard deck of 52 cards.
8 over 13
3 over 13
10 over 13
1 half
Answers
The probability of NOT drawing a face card from a standard deck of 52 cards is 10 over 13.
First determine the total number of face cards and non-face cards in a standard deck of 52 cards. In a standard deck, there are 12 face cards (3 face cards per suit: Jack, Queen, and King, and 4 suits: Hearts, Diamonds, Clubs, and Spades). This means there are 52 - 12 = 40 non-face cards.
Now, we'll calculate the probability of NOT drawing a face card:
Probability = (Number of favorable outcomes) / (Total number of outcomes)
Probability of NOT drawing a face card = (Number of non-face cards) / (Total number of cards)
Probability = 40 / 52
Simplify the fraction by dividing the numerator and denominator by their greatest common divisor (4):
Probability = (40/4) / (52/4)
Probability = 10 / 13
So, the probability of NOT drawing a face card from a standard deck of 52 cards is 10/13. Your answer: 10 over 13.
Learn more about standard deck here: brainly.com/question/31494408
#SPJ11
which measure of variation is affected most by a few extreme scores? which measure of variation is affected most by a few extreme scores? standard deviation mode range median mean
Answers
Standard deviation and median are less affected by extreme scores, while mode is not affected at all since it represents the most frequently occurring value.
The measure of variation affected most by a few extreme scores is the range, as it considers only the difference between the highest and lowest values in a dataset. However, the mean can also be influenced by extreme scores, causing it to deviate from the central tendency. Standard deviation and median are less affected by extreme scores, while the mode is not affected at all since it represents the most frequently occurring value.
learn more about Standard deviation
https://brainly.com/question/23907081
#SPJ11
The measure of variation affected most by a few extreme scores is the range. The range is the difference between the
highest and lowest values in a data set. Extreme scores significantly increase the range, making it a sensitive measure
of variation.
The measure of variation that is affected most by a few extreme scores is the standard deviation.
The reason for this is that the standard deviation is calculated by taking the square root of the sum of squared
deviations from the mean, and the squared deviations from the mean are particularly sensitive to extreme scores.
On the other hand, the mode, range, median, and mean are less affected by a few extreme scores.
The mode is simply the most frequently occurring value in a dataset and is not affected by extreme scores.
The range is the difference between the highest and lowest values in a dataset and can be affected by extreme scores, but only to a limited extent.
The median is the middle value in a dataset, and it is also not affected by extreme scores unless they are extreme
enough to change the position of the middle value.
The mean is the average value in a dataset, and while it can be influenced by extreme scores, its effect is typically less
pronounced than on the standard deviation.
for such more question on range
https://brainly.com/question/2264373
#SPJ11
Mrs. Trout can bake 5 dozen
cookies in 70 minutes. How
many dozen can she bake in
112 minutes?
Answers
Answer:
She can bake 8 dozen cookies in 112 minutes.
Step-by-step explanation:
70/5 =14
112/14= 8
Simplify this numerical expression. (-12)(-13)
Answers
Answer:
156
Step-by-step explanation:
mulitply them, multiplying 2 negative numbers make a positive one. -12 x -13 = 156
Tell whether the following statements are always true, sometimes true or always false./p>
a. If a positive is subtracted from a negative integer, the difference is a negative integer.
b. If a positive integer is subtracted from a positive integer, the difference is a positive integer.
Answers
Each statement about integer is:
"If positive is subtracted from a negative integer, the difference is negative integer" can be sometimes true because when a positive integer is subtracted from a negative integer, the difference can be a negative integer or a positive integer."If a positive integer is subtracted from a negative integer, the difference can be a negative integer or a positive integer" is sometimes true because when a positive integer is subtracted from a negative integer, the difference can be a negative integer or a positive integer.Statement A: If positive is subtracted from a negative integer, the difference is negative integer.
This statement is sometimes true.
If a positive integer is subtracted from a negative integer, the difference can be a negative integer or a positive integer. For example, if -5 is subtracted from -3, the difference is -8, which is a negative integer. However, if -3 is subtracted from -5, the difference is 2, which is a positive integer. The difference sign depends on which value is the bigger one.
Statement B: If a positive integer is subtracted from a positive integer, the difference is a positive integer.
This statement is sometimes true.
If a positive integer is subtracted from a positive integer, the difference can be a positive integer or a negative integer. For example, if 3 is subtracted from 5, the difference is 2, which is a positive integer. However, if 5 is subtracted from 3, the difference is -2, which is a negative integer.
Learn more about Integer here: brainly.com/question/11486291
#SPJ11
There are five children in a room, ages five, six, eight, nine, and twelve. If two children, ages four and twelve, enter the room, what will happen to the mean and standard deviation of ages
Answers
In summary, when the two new children (ages four and twelve) are added to the existing group, the mean age increases from 8 to 8, and the standard deviation changes from its original value to approximately 3.74.
To determine the effect of adding two children (ages four and twelve) to the existing group of five children (ages five, six, eight, nine, and twelve) on the mean and standard deviation of ages, we need to calculate the new values.
Let's calculate the mean first:
Calculate the sum of the ages of the initial five children:
5 + 6 + 8 + 9 + 12 = 40
Add the ages of the two new children:
40 + 4 + 12 = 56
Calculate the new mean by dividing the sum by the total number of children (5 initial + 2 new):
56 / 7 = 8
Therefore, the new mean age is 8.
Now let's calculate the standard deviation:
Calculate the squared difference between each age and the mean for the initial five children:
\((5 - 8)^2 + (6 - 8)^2 + (8 - 8)^2 + (9 - 8)^2 + (12 - 8)^2 = 54\)
Calculate the squared difference between each new age and the new mean:
\((4 - 8)^2 + (12 - 8)^2 = 80\)
Calculate the sum of the squared differences for the initial five children and the new children:
54 + 80 = 134
Divide the sum of squared differences by the total number of children (5 initial + 2 new) and take the square root:
√(134 / 7) ≈ 3.74
Therefore, the new standard deviation is approximately 3.74.
To know more about mean,
https://brainly.com/question/15744601
#SPJ11
Please help brainiest will be the award!

Answers
I think it's how the shading goes all the way to x=5.
The area of triangle PQR is 100 cm?.
25 cm
Q
o
16 cm
R
Calculate the missing angle, 0.

Answers
Answer:
30
Step-by-step explanation:
area of triangle =1/2×sino×25×16
100=200sino
100/200=sino
sino=1/2
sino=sin30
o=30°
Perform the following operation:
h(n) = 4n + 5
g(n) = 3n +4
Find (h - g)(n)
Answers
Answer:
n+1
Step-by-step explanation:
h(n) = 4n + 5
g(n) = 3n +4
(h - g)(n) = 4n + 5 - (3n +4 )
distribute the minus sign
= 4n +5 - 3n -4
Combine like terms
= 4n -3n +5-4
= n +1
1. What is the Least Common Multiple of 2 and 8?
Answers
Answer:
the least common multiple is 8
Need Help!
A line has a slope of 4 and goes through the point (5,−2). What is the equation of this line in Standard Form?
−4x+y=18
4x+y=−18
−4x+y=−18
−4x+y=−22
Answers
Answer:
-4x+y=-22
Step-by-step explanation:
-4x +y= -22 is the equation of this line in Standard Form .
What is in slope-intercept form?
Y = mx + b, which defines a line, is an equation's slope-intercept form.When a line is graphed, its slope, m, and its point of intersection with the y-axis, b, also known as the y-intercept, are shown.To find answers for x, y, m, and b, utilize slope intercept form.m = 4
the point = (5, -2)
the equation of this line
y - y₁ = m ( x - x₁)
y - ( -2 ) = 4 ( x - 5 )
y + 2 = 4( x - 5 )
y + 2 = 4x - 20
y = 4x - 20 - 2
y = 4x - 22
-4x +y= -22
Learn more about slope-intercept form
brainly.com/question/9682526
#SPJ2
15. Describe the three general steps
for producing a recombinant DNA (rDNA) vector, state how rDNA can
be introduced into cells, and discuss the clinical applications of
rDNA.
Answers
Producing rDNA involves isolating and cleaving DNA, inserting fragments into a vector, and transforming host cells. rDNA can be introduced via transformation, transfection, or viral vectors. Clinical applications include protein production, gene therapy, vaccines, and diagnostics.
Producing a recombinant DNA (rDNA) vector involves several general steps. Here are the three main steps involved in the process:
Isolation and Cleavage of DNA:
The first step is to isolate the desired DNA fragments from the source organism. This can be done using various techniques such as PCR (Polymerase Chain Reaction) or restriction enzyme digestion. Restriction enzymes are enzymes that cut DNA at specific recognition sites. By using the appropriate restriction enzymes, the desired DNA fragment and a vector DNA can be cut at specific sites. The vector is usually a plasmid, which is a small circular DNA molecule.
Insertion of DNA Fragments into the Vector:
Once the DNA fragments and vector have been cut, they are mixed together and joined through a process called ligation. DNA ligase is used to catalyze the formation of covalent bonds between the ends of the DNA fragments and the vector. This creates a recombinant DNA molecule containing the desired DNA fragment within the vector. The recombinant DNA molecule is then introduced into host cells for replication.
Transformation of Host Cells:
The recombinant DNA molecules need to be introduced into host cells to produce multiple copies of the recombinant DNA. This is typically done using a process called transformation. Host cells, such as bacteria or yeast, are treated in a way that makes them more receptive to taking up the recombinant DNA. Methods for transformation include heat shock, electroporation, or using chemical agents. Once the host cells have taken up the recombinant DNA, they can be grown in culture to produce large quantities of the desired DNA fragment.
Introduction of rDNA into Cells:
Recombinant DNA can be introduced into cells using various methods, depending on the type of cells being targeted. Some common techniques include:
Transformation: As mentioned earlier, host cells, such as bacteria or yeast, can be treated to make them receptive to taking up the recombinant DNA. This can be achieved by exposing the cells to heat shock, electroporation, or using chemical agents.
Transfection: This method is used for introducing rDNA into eukaryotic cells, including animal cells. It involves the use of techniques such as calcium phosphate precipitation, liposome-mediated transfection, or electroporation.
Viral Vectors: Certain viruses, such as retroviruses, adenoviruses, or lentiviruses, can be modified to carry the recombinant DNA. These viral vectors can then infect target cells and deliver the rDNA into the host genome.
Clinical Applications of rDNA:
Recombinant DNA technology has revolutionized biomedical research and has led to numerous clinical applications. Some important applications include:
Production of Therapeutic Proteins: rDNA technology allows for the production of large quantities of therapeutic proteins, such as insulin, growth factors, clotting factors, and monoclonal antibodies. These proteins can be used to treat various diseases, including diabetes, cancer, and genetic disorders.
Gene Therapy: rDNA vectors can be used to deliver functional copies of genes into target cells to correct genetic defects. This holds promise for the treatment of inherited diseases caused by single gene mutations, such as cystic fibrosis and muscular dystrophy.
Vaccine Development: Recombinant DNA technology has been instrumental in the development of vaccines. By expressing specific antigens from pathogens, recombinant vaccines can be created to stimulate an immune response without causing disease.
Diagnostic Tools: Recombinant DNA techniques are used to produce specific DNA or RNA probes for diagnostic purposes. These probes can detect the presence of specific genes or mutations associated with diseases, aiding in early detection and personalized medicine.
for such more question on isolating
https://brainly.com/question/27746495
#SPJ8
Who has the best conclusion?A.Joe said the average grade was a 75.B.Collin said almost 15% made between a 91 and a 100.C.Paulina said most of the class made between a 71 and a 80.D.Quannah said that most of the students understood the concepts that were not tested.
Answers
Based on the given grade distribution, Paulina's conclusion (C) that most of the class made between a 71 and an 80 is the best conclusion among the options provided.
What is the average?
This is the arithmetic mean and is calculated by adding a group of numbers and then dividing by the count of those numbers. For example, the average of 2, 3, 3, 5, 7, and 10 is 30 divided by 6, which is 5.
To determine who has the best conclusion among Joe, Collin, Paulina, and Quannah, let's evaluate each statement in relation to the given grade distribution:
A. Joe said the average grade was a 75.
Since we have the grade distribution, we can calculate the average grade to verify Joe's statement. However, the distribution alone is not sufficient to determine the average grade. We would need additional information such as the exact values within each grade range. Therefore, we cannot determine if Joe's conclusion is the best based solely on the given information.
B. Collin said almost 15% made between a 91 and a 100.
Based on the given grade distribution, we can calculate the percentage of students who fall within the range of 91-100. In this case, it is 10 students out of a total of 35 students. So, the percentage is approximately 28.6%, not close to 15%. Therefore, Collin's conclusion is not accurate based on the given information.
C. Paulina said most of the class made between a 71 and an 80.
Considering the grade distribution, the largest number of students (12) falls within the range of 71-80. Thus, Paulina's conclusion aligns with the data and can be considered the best conclusion based on the given information.
D. Quannah said that most of the students understood the concepts that were not tested.
The given grade distribution does not provide information about the understanding of concepts. It solely represents the distribution of grades. Therefore, Quannah's conclusion cannot be determined based on the given information.
hence, Based on the given grade distribution, Paulina's conclusion (C) that most of the class made between a 71 and an 80 is the best conclusion among the options provided.
To learn more about the average visit:
https://brainly.com/question/20118982
#SPJ4
