Weatherman Glenn Burns predicts there to be 4.25 inches of rain on Saturday. On Saturday, it actually rains 6.5 inches. How much percent error was Glenn Burns from being accurate?
Answers
Answer:
the prediction was about 35% too low
Step-by-step explanation:
We generally define percent error as the difference between a measurement and an actual value, as a fraction of the actual value. Here, the actual value is 6.5 inches, so we can compute the error to be ...
(4.25 -6.5)/6.5 × 100% = -34.6%
Burns' prediction was about 35% too low.
Related Questions
In a park for 6 people the ticket cost $39. How many dollar does it cost for 9 people
Answers
$ 58.50
Step-by-step explanation:
because 39 Divided by 6 is 6.5 and 6.5 × 9 it's 58 50
$58.50
•EXPLANATION•
The first thing you have to do is divide 39 by 6 to see how much it would cost for 1 person. For 1 person it cost $6.50 then you multiply by 9 because you are trying to figure out how much it cost for 9 people not 1. You will get $58.50.
Charlotte spent $26 at the hair salon. She wants to leave a 12% tip. About how much money should she leave?
Answers
Charlotte spent $26 at the hair salon. She wants to leave a 12% tip. About how much money should she leave?
Remember that
12%=12/100=0.12
Multiply $26 by 0.12 to obtain the tip
so
estimate
0.12-------> 0.10
$26 -----> $30
0.10*30=$3.00
the estimated answer is $3.00Answer: £3.12
Step-by-step explanation: 2% is 0.52
10% is £2.60, adding 0.52 would then equal £3.12
help me pls i hope u have a good day
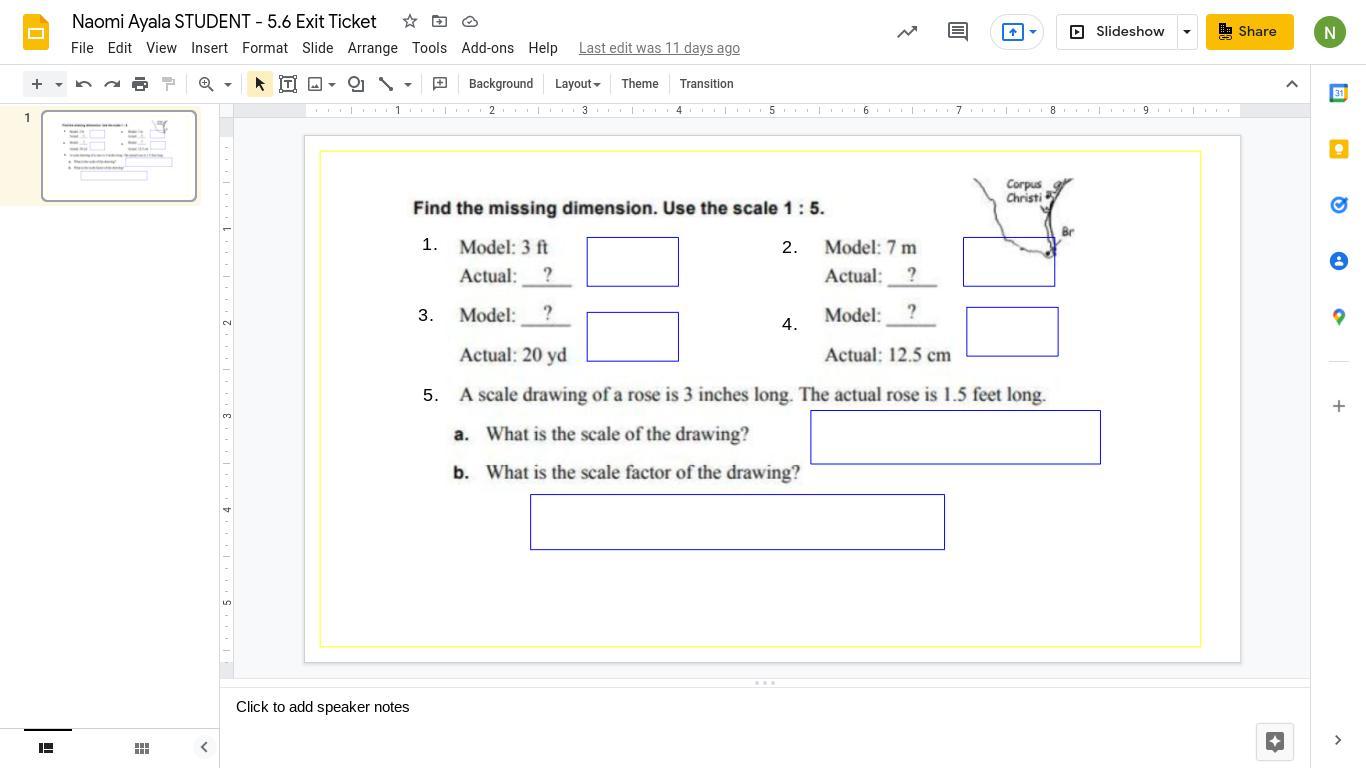
Answers
Answer:
You just multiply by 5. the 1st one will be 15.
1:15
2:35
3:100
4:2.5
5a:1 to 6 or 1:6
5b: I have no idea what this one is sorry.
what is the slope of the line in the graph?

Answers
Answer:
-1 and 1
Step-by-step explanation:
Both numbers touch the line of -1 and 1 on the slope diagram.
x=1
Step-by-step explanation:
ratio of 1 to 1. rise one run one rise over run equals 1
Find the nth term of this number sequence 2, 4, 6, 8, ...
Answers
\(\qquad\qquad\huge\underline{{\sf Answer}}\)
The given sequence is in Arithmetic progression, and we have to find its nth term ~
So, let's get it solved ~
First term of the sequence is :
a = 2Common difference is :
d = 6 - 4 = 4 - 2 = 2Now, if we have to write the 2nd Term with respect to first one, we can write :
2nd Term = a + (2 - 1)d = a + d = 2 + 2 = 4similarly ~
3rd Term = a + (3 - 1)d = a + 2d = 2 + 4 = 64th Term = a + (4 - 1)d = a + 3d = 2 + 6 = 8Therefore, I similar pattern ~
\( \qquad \sf \dashrightarrow \: nth \: term = a + (n - 1)d\)
\( \qquad \sf \dashrightarrow \: nth \: term = 2 + (n - 1)2\)
\( \qquad \sf \dashrightarrow \: nth \: term = 2(1 + (n - 1))\)
\( \qquad \sf \dashrightarrow \: nth \: term = 2(1 + n - 1)\)
\( \qquad \sf \dashrightarrow \: nth \: term = 2 n \)
Feel free to ask your doubts, if you have any ~
Answer:
2nStep-by-step explanation:
from the number sequence above, each term except the first is generated by adding 2 to the term immediately preceding it.
the nth term of the sequence is usually designated Tn, and it's usually a function of n
from the number sequence
T1= 2
T2 = 2+2= 4
T3= 4+2= 6
T4= 6+2= 8
therefore, Tn= 2+2×(n-1)
= 2+2n-2
=2-2+2n= 2n
therefore, the nth term of the number sequence= 2nA company buys machinery for $500000 and pays it off by 20 equal six-monthly instalments, the first payment being made six months after the loan is taken out. If the interest rate is 12%pa, compounded monthly, how much will each instalment be?
Answers
Each installment will be approximately $15,280.55.
To calculate the equal six-monthly installment, we can use the formula for the present value of an annuity.
Principal amount (P) = $500,000
Interest rate (r) = 12% per annum = 12/100 = 0.12 (compounded monthly)
Number of periods (n) = 20 (since there are 20 equal six-monthly installments)
The formula for the present value of an annuity is:
\(P = A * (1 - (1 + r)^(-n)) / r\)
Where:
P = Principal amount
A = Equal installment amount
r = Interest rate per period
n = Number of periods
Substituting the given values into the formula, we have:
$500,000 = \(A * (1 - (1 + 0.12/12)^(-20)) / (0.12/12)\)
Simplifying the equation:
$500,000 = A * (1 - (1.01)^(-20)) / (0.01)
$500,000 = A * (1 - 0.6726) / 0.01
$500,000 = A * 0.3274 / 0.01
$500,000 = A * 32.74
Dividing both sides by 32.74:
A = $500,000 / 32.74
A ≈ $15,280.55
Therefore, each installment will be approximately $15,280.55.
Learn more about Principal amount here:
https://brainly.com/question/30163719
#SPJ11
2. The admission fee at a small fair is $1.50 for children and $4 for adults.
On a certain day, 220 people enter the fair and $505 is collected. How
many children attended the fair that day?
Answers
Answer:
26 children
Step-by-step explanation:
Step 1 Create a system of equations
Firstly, we know that it cost $1.50 for children and $4 for adults and we know that 505$ is the total amount collected
So if x = number of children and y = number of adults
Then 1.50x + 4x = 505
We also know that 220 total people entered which consists of adults and children.
Again, if x = number of children and y = number of adults
Then we can say that x + y = 220
So we now have the two equations
1.50x + 4y = 505 and x + y = 220
Step 2 Solve the equation
There are many methods you can use to solve this equation however I'd recommend the substitution method as we can easily solve for x or y in the equation x + y = 220 and isolate one of the variables, we can then easily substitute that into the other equation.
Isolating y
x + y = 220
==> subtract x from both sides
y = 220 - x
We now substitute y into the other equation and solve for x(# of children)
1.5x + 4y = 505
==> plug in y = 220 - x
1.5x + 4(220 - x) = 505
==> distribute 4
1.5x + 440 - 4x = 505
==> combine like terms
-2.5x + 440 = 505
==> subtract 440 from both sides
-2.5x = -65
==> divide both sides by -2.5
x = 26
So 26 children attended the fair that day.
Consider a motor driven by an external torque r(t) dw(t) }+bw(t)= T(t). dt Given the harmonic input torque given by T(t) = To cos(wft), the particular solution is given by w(t) = Acos(WFt + o). How many seconds does the peak response lag behind the input peak? The answer should be positive. Let J = 3 kg-m^2, b = 58 kg-m^2-S, To = 154 N-m, and w= 16 rad/s. Do not include units, and use three significant figures.
Answers
There will be 0.0451 seconds the peak response lag behind the input peak
The peak response of the system occurs at the same frequency as the input torque, which is given as w_f = 16 rad/s.
The amplitude of the steady-state response can be found using the given equation:
A = T_o / sqrt((Jw² - b²)² + (bw)²)
Substituting the given values, we get:
A = 154 / sqrt((3*(16)² - 58²)² + (58*16)²) ≈ 0.574
The phase angle between the input and output can be found using the equation:
tan(o) = bw / (Jw² - b²)
Substituting the given values, we get:
tan(o) = (5816) / (3(16)² - 58²) ≈ 0.908
Therefore, the phase lag between the input and output is given by:
o = arctan(0.908) ≈ 0.725 radians
To find the time lag, we divide the phase lag by the angular frequency:
t_lag = o / w_f ≈ 0.0451 seconds
Therefore, the peak response lags behind the input peak by approximately 0.0451 seconds.
Learn more about momentum: brainly.com/question/13767949
#SPJ11
A Norman window has the shape of a rectangle surmounted by a semicircle. (Thus the diameter of the semicircle is equal to the width of the rectangle. See the figure below If the perimeter of the window is 24 ft, find the value of x so that the greatest possible amount of light is admitted
Answers
The perimeter equation is:
2x + x + (1/2)πx = 24 ft.
Simplifying the equation, we have:
(5/2)πx + 3x = 24 ft.
To find the value of x, we solve the equation:
(5/2)πx + 3x = 24 ft.
This equation can be solved numerically or algebraically to find the value of x.
The perimeter of a Norman window can be calculated by adding the lengths of all its sides. In this case, the perimeter is given as 24 ft.
Let's break down the components of the Norman window:
- The rectangular part has two equal sides and two equal widths. Let's call the width of the rectangle "x" ft.
- The semicircle on top has a diameter equal to the width of the rectangle, which is also "x" ft.
To find the perimeter, we need to consider the lengths of all sides of the rectangle and the semicircle.
The perimeter consists of:
- Two equal sides of the rectangle, each with a length of "x" ft. So, the total length for both sides of the rectangle is 2x ft.
- The width of the rectangle, which is also "x" ft.
- The curved part of the semicircle, which is half the circumference of a circle with a diameter of "x" ft. The formula for the circumference of a circle is C = πd, where C is the circumference and d is the diameter. So, the circumference of the semicircle is (1/2)πx ft.
To summarize, the perimeter equation is:
2x + x + (1/2)πx = 24 ft.
Simplifying the equation, we have:
(5/2)πx + 3x = 24 ft.
To find the value of x, we solve the equation:
(5/2)πx + 3x = 24 ft.
This equation can be solved numerically or algebraically to find the value of x.
Learn more about Equation here,https://brainly.com/question/29174899
#SPJ11
Abigal found that she can drive 140 miles in 3 hours, including rest stops, on intersate highway. How long would it take her to drive the interstates from cleveland, ohio, to washington dc which is 350 miles?
Answers
Answer:
7.5 hours
Step-by-step explanation:
distance = rate * time (d=rt)
First we find her average rate, or speed:
140 miles = 3 hours * rr = \(\frac{140 miles}{3 hours}\) = 46.6666 miles/hourNow we take that rate and use our second distance to find the time:
d = rt
t = d/r = 350 miles / 46.6666 miles/hour = 7.5 hours
the number of homes sold by a realtor during a month has the following probability distribution: number sold probability 0 0.20 1 0.40 2 0.40 what is the probability that the realtor sells no more than one house during a month?
Answers
The probability that the retailer sells no more than one house in a month is 0.60.
Probability is simply how likely something is to happen. Whenever we're unsure about the outcome of an event, we can talk about the probabilities of certain outcomes and how likely they are to happen. The analysis of events governed by probability is called statistics.
The given is a probability distribution. The probability density function or PDF of the probability is defined for the random variable x, where x ranges from 0 less than or equal to x less than or equal to 2 ie the range of x is from 0 to 2 with 0 and 2 inclusive.
x : 0 1 2
p(x): 0.20 0.40 0.40
The probability that the retailer sells no more than one house in a month is given by
P(x less than or equal to one) = P(0) + P(1)
=0.20 + 0.40 = 0.60.
Learn more about probability at
https://brainly.com/question/11234923?referrer=searchResults
#SPJ4
An automatic filling machine is used to fill 2-litre bottles of cola. The machine’s output is known to be approximately Normal with a mean of 2.0 litres and a standard deviation of 0.01 litres. Output is monitored using means of samples of 5 observations.
Determine the upper and lower control limits that will include roughly 95.5 percent of the sample means.
If the means for 6 samples are 2.005, 2.001, 1.998, 2.002, 1.995 and 1.999, is the process in control?
Answers
The upper control limit (UCL) is approximately 2.0018 litres, and the lower control limit (LCL) is approximately 1.9982 litres, which would include roughly 95.5 percent of the sample means.
Now let's check if the process is in control using the given sample means:
To determine the upper and lower control limits for the sample means, we can use the formula:
Upper Control Limit (UCL) = Mean + (Z * Standard Deviation / sqrt(n))
Lower Control Limit (LCL) = Mean - (Z * Standard Deviation / sqrt(n))
In this case, we want to include roughly 95.5 percent of the sample means, which corresponds to a two-sided confidence level of 0.955. To find the appropriate Z-value for this confidence level, we can refer to the standard normal distribution table or use a calculator.
For a two-sided confidence level of 0.955, the Z-value is approximately 1.96.
Given:
Mean = 2.0 litres
Standard Deviation = 0.01 litres
Sample size (n) = 5
Using the formula, we can calculate the upper and lower control limits:
UCL = 2.0 + (1.96 * 0.01 / sqrt(5))
LCL = 2.0 - (1.96 * 0.01 / sqrt(5))
Calculating the values:
UCL ≈ 2.0018 litres
LCL ≈ 1.9982 litres
Therefore, the upper control limit (UCL) is approximately 2.0018 litres, and the lower control limit (LCL) is approximately 1.9982 litres, which would include roughly 95.5 percent of the sample means.
Now let's check if the process is in control using the given sample means:
Mean of the sample means = (2.005 + 2.001 + 1.998 + 2.002 + 1.995 + 1.999) / 6 ≈ 1.9997
Since the mean of the sample means falls within the control limits (between UCL and LCL), we can conclude that the process is in control.
Learn more about means from
https://brainly.com/question/1136789
#SPJ11
Draw a diagram of the archway modeled by the equation y = x^2 + 5x + 24. Fine and label the y-intercept and the x-intercepts on the sketch. Then find and label the width of the archway at its base and the height of the archway at its highest point, assuming the base of the archway is along the x-axis

Answers
Answer:
1) Please find the attached drawing of the archway created with MS Excel
2) The y-intercept is (0, 24)
The x-intercepts are (-3, 0), and (8, 0)
3) The width of the archway at its base is 11
The height of the archway at its highest point = 30.25
Step-by-step explanation:
1) Please find the attached drawing of the archway created with MS Excel
2) The y-intercept is (0, 24)
The x-intercepts are (-3, 0), and (8, 0)
3) The width of the archway at its base is 11
The height of the archway at its highest point = 30.25
Step-by-step explanation:
The given function representing the archway is y = -x² + 5·x + 24
1) Please find attached the required drawing of the archway created with MS Excel
2) The y-intercept is given by the point where x = 0
Therefore, we have, the y-value at the y-intercept = -0² + 5×0 + 24 = 24
The y-intercept = (0, 24)
The x-intercept is given by the point where y = 0
Therefore, the x-values at the x-intercept are found using the following equation;
0 = -x² + 5·x + 24
x² - 5·x - 24 = 0
By inspection, we have;
x² - 8·x + 3·x - 24 = 0
x·(x - 8) + 3·(x - 8) = 0
∴ (x + 3) × (x - 8) = 0
Either (x + 3) = 0, and x = -3, or (x - 8) = 0, and x = 8
Therefore, the x-intercepts are (-3, 0), and (8, 0)
3) The width of the archway at its base = The distance between the x-values at the two x-intercepts
∴ The width of the archway at its base = 8 - (-3) = 11
The highest point of the arch is given by the vertex of the parabola, y = a·x² + b·x + c, which has the x-value of the vertex = -b/(2·a)
∴ The x-value of the vertex of the given parabola, y = -x² + 5·x + 24, is x = -5/(2×(-1)) = 2.5
Therefore;
The y-value of the vertex, is y = -(2.5)² + 5×2.5 + 24 = 30.25 = The height of the archway at its highest point
∴ The height of the archway at its highest point = 30.25

The vertex of the parabola is at (-2.5, 17.75). And the y-intercept of the parabola is at (0, 24).
What is the equation of the parabola?Let the point (h, k) be the vertex of the parabola and a be the leading coefficient.
Then the equation of the parabola will be given as,
y = a(x - h)² + k
The equation of the parabola is given as,
y = x² + 5x + 24
Convert the equation into a vertex form, then we have
y = x² + 5x + 25/4 - 25/4 + 24
y = (x + 5/2)² + 71/4
y = (x + 2.5)² + 17.75
The vertex of the parabola is at (-2.5, 17.75). The y-intercept of the parabola is given as,
y = (0)² + 5(0) + 24
y = 24
The y-intercept of the parabola is at (0, 24).
More about the equation of the parabola link is given below.
https://brainly.com/question/20333425
#SPJ2

how to find the maximum height of a quadratic equation
Answers
the maximum height of a quadratic equation can be find Use the formula: x = -b / (2a) then Substitute the value of x back into the quadratic equation to find the corresponding maximum height.
To find the maximum height of a quadratic equation, you need to determine the vertex of the parabolic curve. The vertex represents the highest or lowest point of the quadratic function, depending on whether it opens upward or downward.
A quadratic equation is generally written in the form of y = ax² + bx + c, where "a," "b," and "c" are coefficients.
The x-coordinate of the vertex can be found using the formula: x = -b / (2a). This formula gives you the line of symmetry of the parabola.
Once you have the x-coordinate of the vertex, substitute it back into the original equation to find the corresponding y-coordinate.
The resulting y-coordinate represents the maximum height (if the parabola opens downward) or the minimum height (if the parabola opens upward) of the quadratic equation.
Here's an example:
Consider the quadratic equation y = 2x² - 4x + 3.
1. Identify the coefficients:
a = 2
b = -4
c = 3
2. Find the x-coordinate of the vertex:
x = -(-4) / (2 * 2) = 4 / 4 = 1
3. Substitute x = 1 back into the equation to find the y-coordinate:
y = 2(1)² - 4(1) + 3 = 2 - 4 + 3 = 1
Therefore, the maximum height of the quadratic equation y = 2x² - 4x + 3 is 1.
Learn more about quadratic equation here
https://brainly.com/question/30098550
#SPJ4
The maximum height of a quadratic equation can be found by determining the vertex of the parabolic shape represented by the equation. The x-coordinate of the vertex can be found using the formula x = -b / (2a), and the corresponding y-coordinate represents the maximum height.
To find the maximum height of a quadratic equation, we need to determine the vertex of the parabolic shape represented by the equation. The vertex is the point where the parabola reaches its highest or lowest point.
The general form of a quadratic equation is ax^2 + bx + c, where a, b, and c are constants. To find the x-coordinate of the vertex, we can use the formula x = -b / (2a).
Once we have the x-coordinate, we can substitute it back into the equation to find the corresponding y-coordinate, which represents the maximum or minimum height of the quadratic equation.
Let's take an example to illustrate this process:
Suppose we have the quadratic equation y = 2x^2 + 3x + 1. To find the maximum height, we first need to find the x-coordinate of the vertex.
Using the formula x = -b / (2a), we can substitute the values from our equation: x = -(3) / (2 * 2) = -3/4.
Now, we substitute this x-coordinate back into the equation to find the y-coordinate: y = 2(-3/4)^2 + 3(-3/4) + 1 = 2(9/16) - 9/4 + 1 = 9/8 - 9/4 + 1 = 9/8 - 18/8 + 8/8 = -1/8.
Therefore, the maximum height of the quadratic equation y = 2x^2 + 3x + 1 is -1/8.
Learn more:About maximum height here:
https://brainly.com/question/29081143
#SPJ11
Tell whether the relation is a function. Explain your reasoning.
{(-1, 7), (9, 4), (3, -2), (5, 3), (9, 1)}
Answers
If 5x+2=52, then what does x equal?
Answers
Answer:
x=10
Step-by-step explanation:
If we subtract 2 from 52 we get 50 and ten mutiplys into 50.
What is the weight of a 24 square foot 2 inch thick aluminum plate with a unit weight of 15 lbs?
Answers
Weight of a 24 square foot, 2 inch thick aluminum plate will be: 720 lbs.
What is unitary method?A single unit's value can be determined from the values of multiple units, and multiple units' values can be determined from the values of single units using the unitary method.
Given:
Weight of 1 square foot, 1 inch thick plate = 15 lbs.To find: weight of a 24 square foot, 2 inch thick aluminum plate
Finding:
By unitary method, we get:
Weight of 1 square foot aluminum plate = 15 lbs.
Weight of 24 square foot aluminum plate = 15(24) lbs = 360 lbs.
Again, by unitary method, we get:
Weight of 1 square foot, 1 inch thick aluminum plate = 15 lbs.
Weight of 24 square foot, 1 inch thick aluminum plate = 15(24) lbs = 360 lbs.
Weight of 24 square foot, 2 inch thick aluminum plate = 360(2) lbs = 720 lbs.
Hence, Weight of 24 square foot, 2 inch thick aluminum plate = 720 lbs.
To learn more about unitary method, refer to the link: https://brainly.com/question/24587372
#SPJ4
why is part B 80 degrees?

Answers
Answer:
see below
Step-by-step explanation:
Angle B is 100 degrees because vertical angles are equal
<B and angle X are same side interior angles and since AD and EH are parallel lines same side interior angles are complementary
B + X = 180
100 +x = 180
x = 180-100
x = 80
if five arithmetic means are inserted between -9 and 9, what is the third mean?
Answers
Answer:
???????????????????????
Anya’s team won 4 games out of every 9 games this season. If the team played 45 games, how many games did they win?
Answers
Answer:20
Step-by-step explanation:4:9
9x5=45
4x5=20
20:45
What is the range of the relation in the table below?

Answers
The range of the relation is {0, 2, 4}
How to determine the range?The range of the relation are the y values
From the table, we have:
y values = 0, 2, 4, 2, 0
Remove the repetition
y values = 0, 2, 4
Hence, the range of the relation is {0, 2, 4}
Read more about range at:
https://brainly.com/question/10197594
#SPJ1
(8x-4)+(17x-23)+(3x+17)=180
Answers
Answer:
b
Step-by-step explanation:
b
A rectangular pyramid has a height of 10 meters. If the sides of the base measure 3 meters and 5 meters, what is the volume of the pyramid
Answers
Answer:
the volume is 50
Step-by-step explanation:
The volume of a pyramid is found by using the formula V = lwh/3
If you multiply 3 5 and 10 you get 150
Dividing 150 by 3 gives you 50
Find missing angles
X=???

Answers
A simple random sample of 36 cans of regular Coke has a mean volume of 12.19 ounces. Assume that the standard deviation of all cans of regular Coke is 0.11 ounces. Use a 0.01 significance level to test the claim that cans of regular Coke have volumes with a mean of 12 ounces, as stated on the label.
a) State the hypotheses.
b) State the test statistic.
c) State the p-value.
d) State your decision.
e) State your conclusion.
Answers
(a) The Null-Hypotheses is H₀ : μ = 12, Alternate-Hypotheses is Hₐ : μ ≠ 12.
(b) The "test-statistic" is 10.36,
(c) The "p-value" is 0.0001,
(d) We make a decision to reject the "Null-Hypothesis",
(e) We conclude that the cans of "regular-Coke" have volumes with mean different from 12 ounces.
Part (a) : The "Null-Hypothesis" is that the mean volume of cans of regular Coke is 12 ounces, as stated on the label. The alternative-hypothesis is that the mean volume is different from 12 ounces.
So, H₀ : μ = 12
Hₐ : μ ≠ 12.
Part (b) : The "test-statistic" for a one-sample t-test is calculated as:
t = (x' - μ)/(s / √n),
where "s" = sample standard-deviation, μ = population mean, x' = sample mean, and n = sample size,
In this case, x' = 12.19, μ = 12, s = 0.11, and n = 36.
So, t = (12.19 - 12)/(0.11/√36) = 10.36,
Part (c) : We know that for "significance-level" of 0.01. The p-value is 0.0001.
Part (d) : Since the p-value is less than the significance-level of 0.01, we reject the null hypothesis.
Part (e) : Based on the results of the hypothesis test, we can conclude that there is sufficient evidence to suggest that cans of regular-Coke have volumes with a mean different from 12 ounces.
Learn more about Hypotheses here
https://brainly.com/question/24224582
#SPJ4
(0,2) times one half
Answers
Answer:
1
Step-by-step explanation:
2+0=2 so 2 times 1/2 is 1
Discuss whether it is possible that any devices are produced if the production cost is R0,00
Answers
It is safe to say that it is nearly impossible for devices to be produced at zero production costs.
How did we arrive at this assertion?It is highly unlikely that any devices will be produced if the production cost is R0,00 (assuming R refers to South African Rand). There are various factors involved in the production of devices, including the cost of materials and labor, research and development, marketing, and distribution costs.
Even if we disregard the cost of materials and labor, there are still other production expenses that cannot be escaped, like facility costs, machinery, and intellectual property rights. Furthermore, marketing and distribution costs add considerable expenses.
Therefore, it is safe to say that it is nearly impossible for devices to be produced at zero production costs. Even if a device could somehow be developed without incurring any initial costs, other costs incurred during the device's production, such as power costs, facility rent, and salaries, would have to be covered. Therefore the reality is that there is always a cost involved in producing any device, and that cost must be factored in for any real-world production.
learn more about cost of production: https://brainly.com/question/29886282
#SPJ1
Find the midpoint of the line segment from (4,5) to (-4,4)
Answers
9514 1404 393
Answer:
(0, 4.5)
Step-by-step explanation:
The coordinates of the midpoint of a line segment are the average of the coordinates of the end points.
((4, 5) +(-4, 4))/2 = (4-4, 5+4)/2 = (0, 9)/2 = (0, 4.5)\
The midpoint is (0, 4.5).

Question 10 of 10
Which system of inequalities is graphed below? See picture

Answers
Find the slope of the line between the following points:
(27, 11) and (11, 3)
Record your answer in simplest form.
Answers
Answer:
slope = \(\frac{1}{2}\)
Step-by-step explanation:
Calculate the slope m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (27, 11) and (x₂, y₂ ) = (11, 3)
m = \(\frac{3-11}{11-27}\) = \(\frac{-8}{-16}\) = \(\frac{1}{2}\)