What are the coordinates of the point on the directed line segment from (-10, 4) to (-5, -6) that partitions the segment into a ratio of 1 to 4?
Answers
Answer:
answer
Step-by-step explanation:
(-9,2)
Related Questions
What are three consecutive multiples of 3 if 2/3
of the sum of the first
two numbers is 1 greater than the third number?
Answers
The three consecutive multiples of 3 are 15, 18 and 21
To solve this problem
First, let's determine three successive multiples of 3:
The subsequent two would be "x+3" and "x+6" if we call the initial number "x".
Since we are aware that the third number (x+6) is one more than the first two numbers (x + x+3), we can write the following equation:
2/3(x + x+3) = (x+6) + 1
Simplifying this equation, we get:
2/3(2x+3) = x+7
Multiplying both sides by 3, we get:
2(2x+3) = 3(x+7)
Expanding and simplifying, we get:
4x + 6 = 3x + 21
Subtracting 3x and 6 from both sides, we get:
x = 15
Therefore, the three consecutive multiples of 3 are 15, 18 and 21
Learn more about consecutive multiples here : brainly.com/question/22081489
#SPJ1
Use the Distributive Property and mental math to find the product.
5(88) =
Answers
Answer:
440
Step-by-step explanation:
I learned with parenthesis if its like this 4(7)
It usually means to multiply
soo
88 times 5
=440
soo
88
Image below! PLEASE HELP! THIS IS DUE!
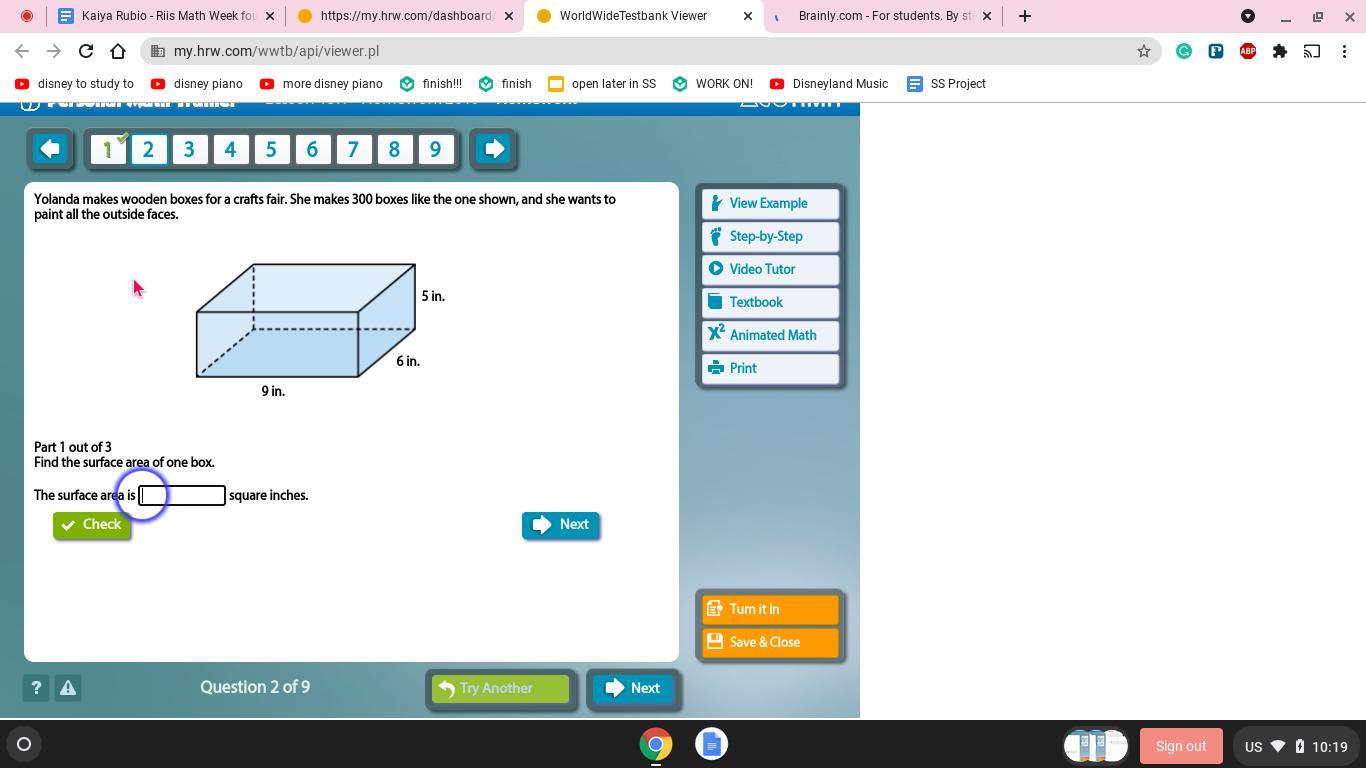
Answers
Answer:
270 if not simplified and
1/1 if simlifies
Step-by-step explanation:
Five added to the sum of -7 and 4
Answers
Answer:
2
Step-by-step explanation:
Five added to the sum of -7 and 4, the phrase "sum of -7 and 4" indicates that we need to add 4 to -7. Do as so :
-7 + 4 = -3
Now we have the portion of "Five added to the [sum]", which shows to add five to the result. :
-3 + 5
= 2
Answer:
the answer is
Step-by-step explanation:
5+4
9-7
2
Hope you like answer
A spinner is divided into 4 sections. The spinner is spun 100 times.
The probability distribution shows the results.
What is P(1≤x≤3)?
Enter your answer, as a decimal, in the box.

Answers
The probability expressed as P(1 ≤ x ≤3) using probability distribution is; 0.90
How to find the spinner probability?We are given that;
Sections in which spinner is divided = 4 sections
Number of times spinner is spun = 100 times
From the probability distribution, we see that;
P(1) = 0.33
P(2) = 0.15
P(3) = 0.42
P(4) = 0.10
Thus;
P(1 ≤ x ≤3) = P(1) + P(2) + P(3)
= 0.33 + 0.15 + 0.42
= 0.9
Read more about Spinner probability at; https://brainly.com/question/3765462
#SPJ1
(PLEASE ANSWER ASAP)

Answers
Answer:
alternate interior angles are congruent
What is 17 percent of 425 please show step by step. I’m really struggling
Answers
Answer:
72.25
Step-by-step explanation:
17% of 425
=17\100 ×425
=7225/100
=72.25
Answer:
72.25
Step-by-step explanation:
Lets say you are trying to find p percent (p%) of a number n. To do this, you would divide the percent (p) by 100 and multiply it by the number (n). In other words:
\(n*\frac{p}{100}\)
We can use this to find 17 percent of 425. 17 would be our percent and 425 would be our number.
\(425*\frac{17}{100}=425*0.17=72.25\)
So 17 percent of 425 would be 72.25.
I hope you find my answer and explanation to be helpful. Happy studying. :)
...........................................................

Answers
Answer:
Top is A bottom is B. ........
Find the original slope of (-6,-1) and (0,3)
Answers
Answer:
slope (m) = 2/3
Step-by-step explanation:
slope = change in x /change in y
Also, slope is y2 - y1 / x2 -x1. That is what I apply for this activity, hence:
slope = 3 - (-1) / 0 - (-6)
= 3 + 1 / 0 + 6
= 4 / 6
= 2/3
∴ slope(m) = 2/3
Identify the graph of y= -2^x+3

Answers
(-3,6] to inequality
Answers
Answer:
-3 < x ≤ 6
Step-by-step explanation:
Left side is exclusive, right side is inclusive, hence the < and ≤, respectively.
The graph below shows the solutions to which inequality?
A. x^2-3x+3 ≥0
B. x² + 3x-3 <0
C. x²-3x+3<0
D. x² + 3x-3>0
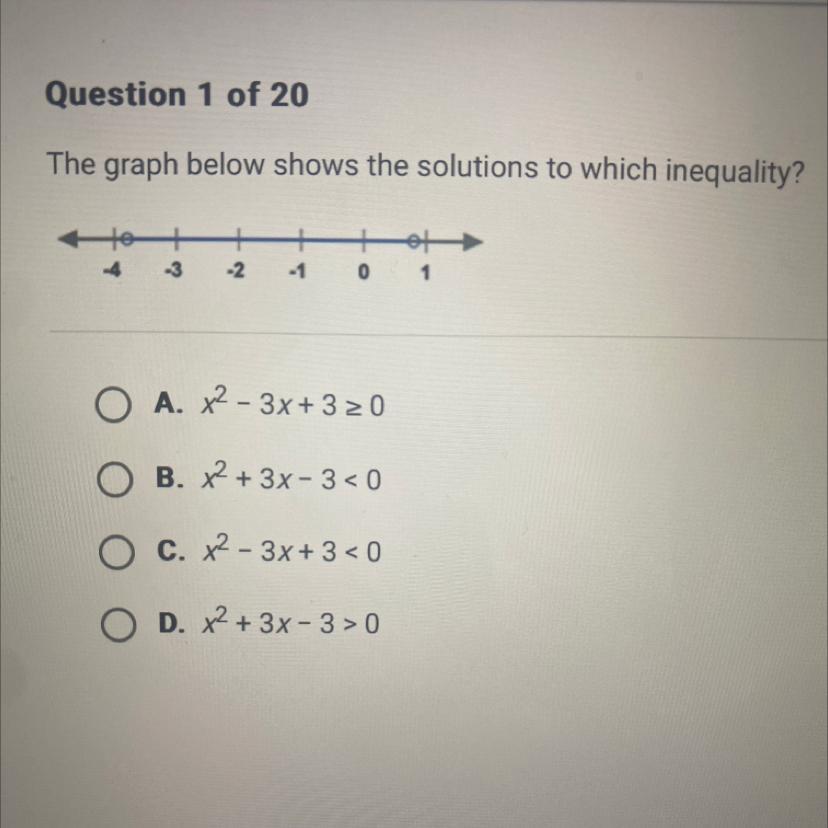
Answers
The inequality expression that corresponds to the solution of the inequality graph is x² + 3x - 3 < 0.
option B.
What is the solution of the inequality?The inequality expression that corresponds to the solution of the inequality graph is determined by simplifying the equations as follows;
The solution of the graph,
x > -4 and x < 1
The first equation with "≥" is ruled out because the graph doesn't have a thick dot.
Let's simplify the second expression;
x² + 3x - 3 < 0
solve using quadratic formula;
x > -3.79 or x < 0.79
The third expression is ruled out since its solution will be complex.
For the last expression;
x² + 3x - 3 > 0
x < -3.79 or x > 0.79
Thus, the correct inequality expression is x² + 3x - 3 < 0.
Learn more about inequality expression here: https://brainly.com/question/25275758
#SPJ1
which equation represents the slope intercept form of the line when the y intercept is (0,-6) and the slope is -5
Answers
The values into the slope-intercept form, we have y = -5x - 6
The slope-intercept form of a linear equation is given by:
y = mx + b
where 'm' represents the slope of the line, and 'b' represents the y-intercept.
In this case, the y-intercept is (0, -6), which means that the line crosses the y-axis at the point (0, -6).
The slope is given as -5.
Therefore, substituting the values into the slope-intercept form, we have:
y = -5x - 6
This equation represents the line with a y-intercept of (0, -6) and a slope of -5.
for such more question on slope-intercept form
https://brainly.com/question/11990185
#SPJ8
need help urgently, don’t think the answers i have are right and i don’t know how to do it!!!

Answers
Answer:
See attached graphy-intercepts = \(\dfrac{3}{2}\)Roots: x = - 3Vertical asymptote: x = -2
Horizontal asymptote y = 1End behavior
\(\mathrm{as}\:x\to \:+\infty \:,\:y\to \:1,\:\:\mathrm{and\:as}\:x\to \:-\infty \:,\:y\to \:1\)
Table:
x y-4 1/2 - 3 0-1 20 3/21 4/32 5/43 6/5Note that the function is undefined at x = -2
Step-by-step explanation:
Given function is
\(f(x) = \dfrac{\left(x^2-9\right)}{\left(x^2-x-6\right)}\)
Part 1
Graph attached
y-intercepts can be found by finding f(0) ie the value of f(x) at x = 0
\(f(0) = \dfrac{\left(0^2-9\right)}{\left(0^2-0-6\right)} = \dfrac{-9}{-6} = \dfrac{3}{2}\)
Roots of a function can be found by setting f(x) = 0 and solving for x
Setting f(x) = 0
==> \(\dfrac{x^2-9}{x^2-x-6} = 0\\\\\)
We can factor the numerator as follows:
x² - 9 = (x + 3) (x -3) since (a + b)(a-b) = a² - b²
Denominator can be factored as follows
x² - x - 6 = (x-3)(x+2)
So
\(f(x) = \dfrac{(x + 3)(x-3)}{(x-3)(x+2)}\\\\\)
The (x-3) term cancels leaving
\(f(x) = \dfrac{x+3}{x+2}\)
Setting this equal to 0 gives
\(\dfrac{x+3}{x+2} = 0\)
This is 0 when x + 3 = 0 or x = -3
So there is only one root and that is x = -3
Asymptotes
The vertical asymptote occurs when at a value of x when the denominator becomes 0
The given function has been factored as
\(f(x) = \dfrac{x + 3}{x + 2}\)
The denominator becomes 0 at x = -2
Vertical asymptote is x = - 2
To find the horizontal asymptote use the fact that when the degrees of the numerator and denominator are equal, the horizontal asymptote is given by
\(y=\dfrac{\mathrm{numerator's\:leading\:coefficient}}{\mathrm{denominator's\:leading\:coefficient}}\)
The degree of the numerator x + 3 is 1 and the degree of the denominator x + 2 is also 1
So the horizontal asymptote is y = 1/1 = 1
y = 1 is the horizontal asymptote
End behavior is the behavior of the function as x → ±∞
This is determined by examining the leading term of the function and determining what its behavior is as x → ±∞
In the function
\(f(x) = \dfrac{x + 3}{x + 2}\)
which is the factored form of the originally given function
the domain of x = all real numbers with the exception of -2 since at x = -2, the function is undefined
The end behavior can be determined by finding the limit of f(x) as x tends to infinity
\(\lim _{x\to \infty \:}\left(\dfrac{x+3}{x+2}\right)\\\\\dfrac{x+3}{x+2} \text{ can be transformed by dividing by x both numerator and denomiator :}\\\\\\=\dfrac{\dfrac{x}{x}+\dfrac{3}{x}}{\dfrac{x}{x}+\dfrac{2}{x}}\\\\\\=\dfrac{1+\frac{3}{x}}{1+\dfrac{2}{x}}\)
\(\lim _{x\to \infty \:}\left(\dfrac{x+3}{x+2}\right) \\\\\\\\=\lim _{x\to \infty \:}\left(\dfrac{1+\dfrac{3}{x}}{1+\dfrac{2}{x}}\right)\\\\\\\\=\dfrac{\lim _{x\to \infty \:}\left(1+\dfrac{3}{x}\right)}{\lim _{x\to \infty \:}\left(1+\dfrac{2}{x}\right)}\)
\(\lim _{x\to \infty \:}\left(1+\dfrac{3}{x}\right) = 1\\\\\lim _{x\to \infty \:}\left(1+\dfrac{2}{x}\right) = 1\)
\(\lim _{x\to \:-\infty \:}\left(\dfrac{x+3}{x+2}\right) = 1\)
End behavior
\(\mathrm{as}\:x\to \:+\infty \:,\:y\to \:1,\:\:\mathrm{and\:as}\:x\to \:-\infty \:,\:y\to \:1\)
Table:
x y
-4 1/2
- 3 0
-1 2
0 3/2
1 4/3
2 5/4
3 6/5
Note that the function is undefined at x = -2

Equation A is equal to (C + D) x (C + D). Equation B is equal to 2 x (C + D). If C and D were numbers that were greater than zero, which equation would give you a bigger value ? Equation A or Equation B ? Give an example for C and D that supports your answer. PLEASE HELP TIMED EXAM!!!!!
Answers
According to the question an example of C = 3 and D = 2 supports the answer that Equation A gives a bigger value than Equation B.
What is equation?Two equations are considered to be comparable when their roots and solutions line up. To create an equivalent equation, the identical quantity, symbol, or expression has to be added to or removed from both of the equation's two sides. We can also create a similar equation by dividing or multiplying each component of an equation with a nonzero value.
given,
To determine which equation would give a bigger value, we can compare the expressions obtained by expanding Equation A and simplifying Equation B.
Expanding Equation A, we get:
A = (C + D) x (C + D) = C² + 2CD + D²
Simplifying Equation B, we get:
B = 2 x (C + D) = 2C + 2D
To compare the values of A and B, let's choose some values for C and D that are greater than zero. Let's choose C = 3 and D = 2.
Plugging these values into Equation A, we get:
A = 3² + 2(3)(2) + 2² = 9 + 12 + 4 = 25
Plugging these values into Equation B, we get:
B = 2(3 + 2) = 2(5) = 10
Since A is greater than B for the values of C = 3 and D = 2, we can conclude that Equation A gives a bigger value than Equation B for positive values of C and D.
Therefore, an example of C = 3 and D = 2 supports the answer that Equation A gives a bigger value than Equation B.
To know more about equation visit:
brainly.com/question/2972832
#SPJ1
the three cards below form a number pattern. The first two cards have been turned over to show their numbers
2 4 ?
What number could be on 3rd card and what rule have you used to find this number
Answers
Answer:
Most likely answers are either 6 or 8.
Step-by-step explanation:
The sequence could be of all even numbers, so 2, 4, 6, 8, etc.
Or of all powers of 2, starting at 2, so 2, 4, 8, 16, etc.
Since there are an infinite number of sequences that fit the pattern, you just have to choose the most likely.
Answer:
hey mate here is ur answer:---------------------------------------------------Most likely answer either 6or 8The sequence could be all even number so, 2,4,6,8 etc.... or of all powers of 2,starting at 2,so,2,4,8,16etc.......since there are an infinity numbers of sequences that still the pattern, you just have to choose most likely.I hope this helps u have a nice day ❤✌☘geometric series $b 1 b 2 b 3 \cdots b {10}$ has a sum of $180$. assuming that the common ratio of that series is $\dfrac{7}{4}$, find the sum of the series $b 2 b 4 b 6 b 8 b {10}.$
Answers
The sum of the series b 2 b 4 b 6 b 8 b {10} is \($\dfrac{180}{3}$\) since it is a geometric series with a common ratio of \($\dfrac{7}{4}$\).
Since the given series \($b 1 b 2 b 3 \cdots b {10}$\) has a sum of 180, it can be deduced that the series is a geometric series with a common ratio of\($\dfrac{7}{4}$\). This means that the ratio of any two consecutive terms in the series is a constant, \($\dfrac{7}{4}$\). Therefore, the sum of the series b 2 b 4 b 6 b 8 b {10} can be calculated as follows:
\($S = b2 + b4 + b6 + b8 + b_{10}$\)
\($= b2\left(\dfrac{7}{4}\right)^0 + b2\left(\dfrac{7}{4}\right)^2 + b2\left(\dfrac{7}{4}\right)^4 + b2\left(\dfrac{7}{4}\right)^6 + b2\left(\dfrac{7}{4}\right)^8$\)
\($= b2 \left[1 + \left(\dfrac{7}{4}\right)^2 + \left(\dfrac{7}{4}\right)^4 + \left(\dfrac{7}{4}\right)^6 + \left(\dfrac{7}{4}\right)^8\right]$\)
\($= b2 \left[\dfrac{1-\left(\dfrac{7}{4}\right)^{10}}{1-\left(\dfrac{7}{4}\right)^2}\right]$\)
\($= b2 \left[\dfrac{1-\left(\dfrac{7}{4}\right)^{10}}{\dfrac{3}{4}}\right]$\)
\($= \dfrac{4b2}{3} \left[1-\left(\dfrac{7}{4}\right)^{10}\right]$\)
Since the sum of the series\($b 1 b 2 b 3 \cdots b {10}$\) is 180, we can substitute $b2$ with \($\dfrac{180}{3}$\)nd calculate the sum of the series $b 2 b 4 b 6 b 8 b {10}$:
\($S = \dfrac{4\left(\dfrac{180}{3}\right)}{3} \left[1-\left(\dfrac{7}{4}\right)^{10}\right]$\)
\($= \dfrac{180}{3} \left[1-\left(\dfrac{7}{4}\right)^{10}\right]$\)
Therefore, the sum of the series \($b 2 b 4 b 6 b 8 b {10}$ is $\dfrac{180}{3}$\).
Learn more about ratio here
https://brainly.com/question/13419413
#SPJ4
in your brains you want a ___ between excitary and inhibitroy signals
Answers
In brains, we want a balance between excitatory and inhibitory signals to maintain proper neural functioning.
Since, We know that;
In brains, we want a balance between excitatory and inhibitory signals to maintain proper neural functioning.
This balance is important because too much excitatory signaling can cause overstimulation and potential harm, while too much inhibitory signaling can lead to neural suppression and lack of responsiveness.
Hence, The proper balance between the two types of signals is necessary for healthy neuronal activity, and maintaining that balance is a key aspect of neural health.
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1
A community would like to add a brick paver border around their swimming pool. They created the following image to represent the pool with the border. A large rectangle with a length of 48 feet and a width of 28 feet. Inside of it is another rectangle with a length of 32 feet and a width of 12 feet. Part A: Find the total area of the brick paver border that surrounds the 12 ft by 32 ft pool. Show your work. (2 points) Part B: If brick pavers cost $8 per square foot, what is the total cost of the brick pavers needed for this project? Explain. (2 points)
Answers
Part A: The total area of the brick paver border is \(960\) square feet.
Part B: The total cost of the brick pavers needed for this project is $\(7,680\).
Part A: To find the total area of the brick paver border, we need to subtract the area of the pool from the area of the larger rectangle. The area of the pool is \(32\) feet multiplied by 12 feet, which is equal to \(384\)square feet.
The area of the larger rectangle is \(48\) feet multiplied by \(28\) feet, which is equal to \(1,344\) square feet. Therefore, the area of the brick paver border is \(1,344\) square feet minus \(384\) square feet, which equals \(960\) square feet.
Part B: If brick pavers cost $\(8\)per square foot, we can calculate the total cost by multiplying the cost per square foot by the total area of the brick paver border. The total area of the brick paver border is \(960\) square feet, and the cost per square foot is $\(8\).
Therefore, the total cost of the brick pavers needed for this project is $\(8\)multiplied by \(960\) square feet, which equals $\(7,680\).
Note: The calculations provided assume that the border consists of a single layer of brick pavers.
For more such questions on area:
https://brainly.com/question/2607596
#SPJ8
you're valuing horn of plenty mining, inc.'s, stock in order to compare its value to its market price. you believe that the company will pay total dividends of $1.45 in 2015 and $1.56 in 2016. you also believe the company's stock price will be $35.80 at the end of 2016. if the appropriate discount rate is 12 percent, what's the value of horn of plenty mining's stock? a. $39.22 b. $38.31 c. $36.87 d. $37.43
Answers
Step 1: Calculate the present value of each dividend payment.
PV(2015) = $1.45 / (1 + 0.12)^1 = $1.29
PV(2016) = $1.56 / (1 + 0.12)^2 = $1.22
Step 2: Calculate the present value of the expected stock price at the end of 2016.
PV(2016 stock price) = $35.80 / (1 + 0.12)^2 = $28.33
Step 3: Add up the present values of the dividend payments and stock price to get the total stock value.
Stock value = PV(2015) + PV(2016) + PV(2016 stock price) = $1.29 + $1.22 + $28.33 = $30.84
Therefore, the value of Horn of Plenty Mining's stock is $30.84, which means that the correct option is e) None of the above.
NEED HELP ASAP The equation of line a is: -x + 4y = 32
How do theses equations compare to line a?
y=1/4x + 1
-4x+y=-8
4x+y=-3

Answers
y = 1/4x + 1 is parallel to line a
-4x + y = -8 is neither parallel nor perpendicular to line a
4x + y = -3 is perpendicular to line a
Parallel and Perpendicular linesFrom the question, we are to determine how the given equations compare to line a.
From the given information,
Line a is -x + 4y = 32
First, we will determine the slope of line a
To do this, we will compare the equation to the slope-intercept form of a line
The slope-intercept form of a line is
y = mx + b
Where m is the slope
and b is the y-intercept
Writing -x + 4y = 32 in the slope-intercept form
-x + 4y = 32
4y = x + 32
Divide through by
y = 1/4 x + 8
By comparison, the slope of line a is 1/4
NOTE: If two lines are parallel, their slopes will be equal
and
If two lines are perpendicular, their slopes will be the negative reciprocal of each other
Now, we will determine the slopes of each of the lines
For y = 1/4x + 1
By comparing with the slope-intercept form of a line, y = mx + b
The slope of the line is 1/4
Thus, the line is parallel to line a
For -4x+y=-8
Rewrite in the slope-intercept form of a line
-4x + y = -8
y = 4x - 8
By comparing with the slope-intercept form of a line, y = mx + b
The slope of the line is 4
4 is not equal to 1/4 and 4 is not the negative reciprocal of 1/4.
Thus, the line is neither parallel nor perpendicular to line a.
For 4x+y=-3
Rewrite in the slope-intercept form of a line
4x + y = -3
y = -4x - 3
By comparing with the slope-intercept of a line, y = mx + b
The slope of the line is -4
-4 is the negative reciprocal of 1/4.
Thus, the line is perpendicular to line a.
Learn more on Parallel and Perpendicular lines here: https://brainly.com/question/7396586
#SPJ1
During second period, Janet completed a grammar worksheet. She got 14 questions correct and 42 questions incorrect.
Part A: What percentage did Janet get correct
_________%
Part B: What percentage did Janet get incorrect?
A: 50%
B: 65%
C: 75%
D: 80%

Answers
Answer:
A=33.33
Step-by-step explanation:
Answer: Part A) 25%
Part B) 75%
Step-by-step explanation: Hope this helps.
A crime is committed by one of two suspects, A and B. Initially, there is equal evidence against both of the suspects. After further investigation, it is determined that the guilty party has a blood type found in only 10% of the population at large. Suspect A does have this blood type; the blood type of Suspect B is unknown.
Define the following 3 events A, M and C.
A: "A is guilty" (Thus ° denotes "B is guilty')
M: "A’s blood type matches that of the guilty party"
C: "B's blood type matches that of the guilty party"
A. The police reported that suspect A is not a relative of suspect B. Is it reasonable to set P( MA)=P(C|A)=10%? Why?
B. Assume that P(MAC)=P(C|A)=10%. Given the information from the further investigation of the crime scene, what is the probability that A is the guilty party?
C. Assume that P( MA)=P(C/A)=10%. Given the information from the further investigation of the crime scene, what is the probability that B’s blood type matches that of the guilty party?
Answers
Answer:
a) MA conditional with C can be interpreted as A which is known and C which is unknown match
b) 10/11
c) 2/11
Step-by-step explanation:
A={A is the guilty party}
\(M_A\) = {A blood type matches that of the guilty party}
C = {B is the guilty party}
\(M_C\) = {B blood type matches that of the guilty party}
a) The chance is 10% because MA conditional with C can be interpreted as A which is known and C which is unknown match
b) the probability that A is the guilty party is given by \(P(A/M_A)\). Using bayes theorem:
\(P(A/M_A)=\frac{P(M_A/A)P(A)}{P(M_A/A)P(A)+P(M_C/C)P(C)} =\frac{1*1/2}{(1*1/2)+(1/10*1/2)} =\frac{10}{11}\)
c) the probability that B’s blood type matches that of the guilty party is given as \(P(M_C/M_A)\). Using LOTS Therefore:
\(P(M_C/M_A)=P(M_C/M_A,A)P(A/M_A)+P(M_C/M_A,A)P(C/M_A)=\frac{1}{10}*\frac{10}{11} +1*\frac{1}{11} =\frac{2}{11}\)
A sequence is defined by the function A(n) =8+ (n -1)(-4).
Which term, n, would result in A(n) = -172?
A) 44
B) 46
C)692
D)700
Answers
Answer:
B. 46.
Step-by-step explanation:
First we set up the equation A(n)=-172 and substitute the given equation for A(n), giving us -172=8+(n-1)(-4). Simplifying, we get -180=(-4n+12), or -4n=-192, or n=48. However, n represents the number of terms in the sequence, and since the sequence starts with n=1, we need to subtract 1 from our answer to get the term number corresponding to A(n)=-172. Therefore, the answer is B) 46.
If x = 8 units, y = 5 units, and h = 3 units, then what is the area of the parallelogram shown above?
Answers
Answer:
Area of Parallelogram Using Diagonals ; Using Base and Height, A = b × h ; Using Trigonometry, A = ab sin (x) ; Using Diagonals, A = ½ × d1 × d2 .....
Using Diagonals: A = ½ × d1 × d2 sin (y)
Using Base and Height: A = b × h
Using Trigonometry: A = ab sin (x)
In the Gaussian integral, how does the left side of this equation equal the right side? An answer would be really appreciated, thank you.

Answers
the left side of this equation equal the right side through the process of completing the square that establishes the equality between the left side and the right side of the Gaussian integral equation.
How do we calculate?
using completing the square method:
Starting with the left side of the equation:
∫\(e^(^-^x^2)\) dx
\(e^(^-^x^2) = (e^(^-x^2/2))^2\)
∫\((e^(^-^x^2/2))^2 dx\)
let u = √(x²/2) = x = √(2u²).
dx = √2u du.
∫ \((e^(^x^2/2))^2 dx\)
= ∫ \((e^(^-2u^2)\)) (√2u du)
The integral of \(e^(-2u^2)\)= √(π/2).
∫ \((e^(-x^2/2))^2\) dx
= ∫ (√2u du) \((e^(-2u^2))\\\)
= √(π/2) ∫ (√2u du)
We substitute back u = √(x²/2), we obtain:
∫ \((e^(-x^2/2))^2\)dx
= √(π/2) (√(x²/2))²
= √(π/2) (x²/2)
= (√π/2) x²
A comparison with the right side of the equation shows that they are are equal.
Learn more about Gaussian integral equation at:
https://brainly.com/question/33550421
#SPJ1
1. (x - 2) + (3x + 8)
Answers
Answer:
4x+6
Step-by-step explanation:
(x-2) + (3x + 8)
combine like terms
4x + 6
Hope this helps!!!
Answer:
4x+6
Step-by-step explanation:
she sells 6adult tickets and 5 children tickets on the first day totaling $112.50 and on the second day she sells 8adult tickets and 4 childrens tickets totaling $130. write an equation for each day and use the elimination method
Answers
Answer:
Cost of adult ticket = $12.5
Cost of child ticket = $7.5
Step-by-step explanation:
Given:
Cost of 6 adult ticket and 5 child ticket = $112.5
Cost of 8 adult ticket and 4 child ticket = $130
Find:
Equation and solution
Computation:
Assume;
Cost of adult ticket = a
Cost of child ticket = b
So,
6a + 5b = 112.5....eq1
8a + 4b = 130 ......eq2
Eq2 x 1.25
10a + 5b = 162.5 .....eq3
eq3 - eq1
4a = 50
Cost of adult ticket = $12.5
8a + 4b = 130
8(12.5) + 4b = 130
Cost of child ticket = $7.5
GREATEST COMMON FACTORFactor the expression completely.40+25x
Answers
we have the expression
40+25x
Remember that
40=(2)(2)(2)(5)
25=(5)(5)
so
GCF=5
therefore
40+25x=5(8+5x)
the answer is
5(8+5x)GCF=5how would you know if a polynomial is prime?