What are the coordinates of the y-intercept of the line whose
equation is 10x + 7y= 5?

Since, Alice ate 5 cookies and 2 carrots for a total of 590 calories; bob ate 3 cookies and 4 carrots for a total of 410 calories. Therefore, In a cookie there are 110 calories.

A calorie is a unit of energy that food and drink provide. we can usually find out how many calories are listed in foods, and wearables like the best fitness trackers let you monitor how many calories you're burning in different activities. Certain foods, such as processed foods, tend to be high in calories. Other foods, such as fresh fruits and vegetables, tend to be low in calories. there is not. Calories are needed to give you enough energy to move, keep warm, grow, work, think, and play. Our circulation and digestion also need to work well with the energy we get from calories.

Let x = calories in cookies.

     y = calories in carrots.

Now, according to the question:

     5x + 2y = 590                   --------------------------------------- (1)

     3x + 4y = 410                    -------------------------------------- (2)

Multiplying equation(1) by 3 and equation(2) by 5:

         15x + 6y = 1770                       ---------------------------(3)

         15x + 20y = 2050                   ---------------------------(4)

Solving we get:

    y = 280/14

or, y = 20 units.

Putting the value of y = 20 in equation (2)

    3x + 4y = 410

⇒  3x + 4 × 20 = 410

⇒ 3x = 410 - 80

⇒ x = 330/3

⇒ x = 110 Units

Therefore, the calories of cookies is 110 units .

Learn more about Calories:

https://brainly.com/question/17078881

#SPJ4

Using the triangle inequality theorem, the largest possible whole-number length for the third side is 4.

The third side of a triangle must be shorter than the sum of the other two sides and longer than the difference between the other two sides.

So, for a triangle with sides of length 1, 4, and x (where x is the length of the third side), we have:

1 + 4 > x

4 + x > 1

1 + x > 4

Simplifying these inequalities, we get:

5 > x

x > 3

x > -3 (this inequality is always true)

The largest possible whole-number length for the third side is 4, since it is the largest integer that satisfies the above inequalities.

Learn more about the triangle inequality theorem on:

https://brainly.com/question/309896

#SPJ1

Answer:

hsvxnosh jwydtko isgrekon dtdorny

For the algorithm that requires f(n) bit operations with the given function f(n),  Thus, the largest n for which one can solve within a day using an algorithm that requires f(n) bit operations with the given function f(n) are:Part \(A: n ≈ 3,166Part B: n ≈ 96Part C: n ≈ 11\)

Hence, the number of bit operations in a day will be\((24 * 60 * 60 * (10^11)) / (10^-11) = 8.64 × 10^21.For f(n) = 1000n^2\),

the number of bit operations is \(f(n) = 1000n^2.If we set f(n) equal to 8.64 × 10^21,\)

we can solve for n:\(8.64 × 10^21 = 1000n^2n^2 = 8.64 × 10^18n ≈ √(8.64 × 10^18 / 1000)n ≈ 3,166\)Part B:For the algorithm that requires f(n) bit operations with the given function f(n), the largest n can be solved within a day is 96 using the given function \(f(n) = 2^n\), where each bit operation is carried out in 10-12 seconds.

Hence, the number of bit operations in a day will be \((24 * 60 * 60 * (10^4)) / (10^-4) = 8.64 × 10^10.\)

For\(f(n) = 22n,\)

the number of bit operations is\(f(n) = 22n.\)

If we set f(n) equal to \(8.64 × 10^10\), we can solve for n:\(8.64 × 10^10 = 22nn ≈ log2(8.64 × 10^10) / log2(2^2)n ≈ 11\)

To know more about function visit:

https://brainly.com/question/30721594

#SPJ11

Answer:

Exact Area = 24pi square cm

Approximate Area = 75.36 square cm  (when using pi = 3.14)

Note: "square cm" can be abbreviated to "cm^2" without quotes.

=============================================================

Explanation:

Let's find the area of the full circle with radius r = 12

A = pi*r^2

A = pi*12^2

A = 144pi  

This is the exact area of the full circle in terms of pi. To get the approximate area, you would replace pi with something like 3.14 (though you could use more decimal digits in pi to get a more accurate area).

We found the area of the full circle, but we only want a pie slice of it. Each slice is 60 degrees, out of 360 total. So that means we want 60/360 = 1/6 of the full area.

In other words, there are 6 slices because 360/60 = 6, which means we'll divide the area we got by 6

(144pi)/6 = (144/6)pi = 24pi

The exact area of the pie slice is 24pi square cm

If you used the approximation pi = 3.14, then that leads to an approximate answer of 24*pi = 24*3.14 = 75.36 square cm

The diver collected water samples at every 3 meters, starting from 5 meters below the water surface, up to a final depth of 35 meters.

We can find the number of samples collected by dividing the total depth range by the distance between each sample and then adding 1 to include the first sample.

The total depth range is:

35 m - 5 m = 30 m

The distance between each sample is 3 m, so the number of samples is:

(30 m) / (3 m/sample) + 1 = 10 + 1 = 11

Therefore, the diver collected a total of 11 water samples.

Answer:

the answer would be c=81x^28-n I hope it helps!

Answer:

c=81x^28-n

Step-by-step explanation:

\(c=81x^{28-n}\)

The correct answer is C. dV = πr^2 0h dr. This is because the formula for the volume of a right circular cylinder is V = πr^2h. To estimate the change in volume, we take the derivative with respect to r:dV/dr = 2πrh

To estimate the change in volume when the radius changes from r0 to r0 dr, we multiply both sides by dr:

dV = 2πrh0 dr

Since the height does not change, we can substitute h0 for h:

dV = 2πr0h0 dr

Finally, we can use the formula for the volume of a cylinder to substitute πr^2 for h0:

dV = πr^2 0h dr

Therefore, the correct answer is C.

The differential formula that estimates the change in the volume (dV) of a right circular cylinder when the radius changes from r0 to r0 + dr and the height does not change is:

dV = 2πr0h dr

So, the correct answer is B. dV = 2πr0h dr.

Visit here to learn more about Volume of a Cylinder:

brainly.com/question/27033747

#SPJ11

Answer:

  24.1 billion

Step-by-step explanation:

One way to write the logistic function is ...

  P(t) = AB/(A +(B-A)e^(-kt))

where A is initial value (P(0)), and B is the carrying capacity (P(∞)). We are told to use relative population growth in the 1990s as the value for k.

In billions, we have ...

  A = 5.3

  B = 100

  k = 0.02/5.3 ≈ 0.003774 . . . . . relative growth rate at 20 M per year

  t = 2450 -1990 = 460

  \(P(t)=\dfrac{530}{5.3+94.7e^{-0.003774t}}\\\\P(460)=\dfrac{530}{5.3+94.7e^{-1.73604}}\approx \boxed{24.1\quad\text{billion}}\)

Hey there! I'm happy to help!

We start out with 3.

3

Our mom gives us 10.

3+10=13

Our dad gives us 30.

13+30=43

Our aunt and uncle give us 100.

43+100=143

And we have another 7.

143+7=150

Therefore, we have $150 now.

Have a wonderful day! :D

Part a:  10z > 25,670; infinite integer.

Part b: Range =  2550 to 2649.

Part a:  10z > 25,670

Divide the inequality on both sides by 10.

z >  2,567

Thus, there are infinite number which are greater than 2567.

Part b:  z rounded to the nearest hundred is 2,600.

Range =  2550 to 2649.

To know more about the integer, here

https://brainly.com/question/17383603

#SPJ4

Answer:

B

Step-by-step explanation:

A(-3 , 3) -> A'(-9 , 9)

B(3 , 3) -> B'(9 , 9)

C(3 , 0) -> C'(9 , 0)

A'B'C' is a dilation of ABC about the origin with factor of 3

ΔA'B'C' ~ ΔABC: all the corresponding angles are the same measurement

In the given problem, we are given a parallelogram ABCD with the conditions that ∠GEC is congruent to ∠HFA and AE is congruent to FC. We need to prove that triangle GEC is congruent to triangle HFA.

To prove that triangle GEC is congruent to triangle HFA, we can use the Side-Angle-Side (SAS) congruence criterion.

Given that AE ≅ FC and ∠GEC ≅ ∠HFA, we have two sides and the included angle that are congruent.

Now, since ABCD is a parallelogram, opposite sides are parallel and congruent. Therefore, AD ≅ BC and AB ≅ DC.

By using the corresponding parts of congruent triangles, we can conclude that EG ≅ HF (opposite sides of a parallelogram) and EC ≅ FA (opposite sides of a parallelogram).

Now, we have all three sides of triangle GEC congruent to the corresponding sides of triangle HFA, satisfying the SAS congruence criterion.

Therefore, by the SAS congruence criterion, we can conclude that triangle GEC is congruent to triangle HFA.

Learn more about parallelogram here:

https://brainly.com/question/32033686

#SPJ11

Answer:

Step-by-step explanation:

y=−3x+12

when x=0 then y=12 , the y intercept is (0,12)

when y=0 then -3x+12=0, -3x=-12, x=12/3=4

x intercept =(4,0)

The x and y intercepts of the line are (4, 0) and (0, 12).

In Maths, an intercept is a point on the y-axis, through which the slope of the line passes. It is the y-coordinate of a point where a straight line or a curve intersects the y-axis. This is represented when we write the equation for a line, y = mx+c, where m is slope and c is the y-intercept.

To find the x-intercept, substitute in 0 for y and solve for x. To find the y-intercept, substitute in 0 for x and solve for y.

When y=0, we get

x=4

So, x-intercept is (4, 0)

When x=0, we get

y=12

So, y-intercept is (0, 12)

Therefore, the x and y intercepts of the line are (4, 0) and (0, 12).

To learn more about the y-intercept visit:

brainly.com/question/14180189.

#SPJ2

Answer:

ML = √[¼ (EC)²]

Step-by-step explanation:

ML² = ½(QR)²

QR² = ½(EC)²

so, ML² = ¼ (EC)²

=> ML = √[¼ (EC)²]

The equation of the line ML is given by \(ML = \frac{AC}{2\sqrt{2} }\)   .

Thus, the equation of the line ML is given by \(ML = \frac{AC}{2\sqrt{2} }\)   .

Learn more about parallelogram here:
https://brainly.com/question/970600

#SPJ2

Answer:

Answer is D) 42x − 24

Step-by-step explanation:

Opening the expression given in question

6(7x − 4)

6 will be multiplied by both items present inside parenthesis.

it can be written as

={(6 * 7x) - (6*4)}

=42x-24

Hope that clears the question.

The expected value to the nearest dollar is 4895.

Probability refers to a possibility that deals with the occurrence of random events.

The probability of all the events occurring need to be 1.

Given that Amount of Claim $0 $2000 $4000 $6000 $8000 $10000

Probability 0.70 0.15 0.08 0.05 0.01 0.01

Therefore, Expected value E(x) = Σx * p(x)

E(x) = - 5(0.999999) + 4899999995(0.000001)

E(x) = - 4.999995 + 4899.999995

E(x) = 4895

Hence, expected value is 4895

Learn more about probability here;

https://brainly.com/question/9326835

#SPJ1

Answer:

259.5

Step-by-step explanation:

8.1*12=97.2
Area of trapiezium = 1/2(b+a)h
(2.8+8.1)=10.9
10.9*3/2=16.35
16.35*2=32.7
2.8*12=33.6
33.6+32.7+97.2=163.5
4*12*2=96
163.5+96=259.5

The first monthly charge has about $78.78 allotted in the direction of reducing the principal.

The total buy charge of the house is $96,400 and the Spinoses made a 25% down payment, because of this they paid $96,400 x 0.25 = $24,100 in advance.

Therefore, the final quantity that they financed is $96,400 - $24,100 = $72,300.

They financed this amount at 5.50% for 30 years, which gives us the following method for calculating the monthly payment (P):

P = (r * PV) / (1 - (1 + r)^(-n))

in which:

Substituting the values, we get:

P = (0.00458 * 72,300) / (1 - (1 + 0.00458)^(-360))

P ≈ $410.66

We recognise that the monthly payment is $410.66 and we will calculate the interest portion of the primary monthly price as follows:

interest = balance * monthly interest price

interest = $72,300 * (5.50% / 12) ≈ $331.88

To calculate the amount of the primary monthly charge this is used to lessen the fundamental, we subtract the interest component from the total monthly payment:

$410.66 - $331.88 ≈ $78.78

Thus, the first monthly charge has about $78.78 allotted in the direction of reducing the principal.

Learn more about Present value formula:-

https://brainly.com/question/20813161

#SPJ4

The amount of interest for the year was 3,770 cents, and the regular price of the electric drill that Pamela bought before the discount was 21,927 cents

Interest = P x R x T.

Where:

P = Principal amount (the beginning balance).

R = Interest rate

T = Number of time periods

In this case, we are given that;

Principal amount (P) = $580

Interest rate (R) = 6,5 %

Time = 1 year

Hence, The amount of the interest = 6,5% of $580

                                                     = 0.065 × $580

                                                     = $37.7

1 dollar = 100 cents

Hence, $37.7 = 37.7 × 100 cents equal to 3,770 cents

P = (1 – d) x

Where,

P = Price after discount

D = discount rate

X = regular price

In this case, we are given that:

P = $32.89

D = 85% = 0,85

Hence, the regular price:

P = (1 – D) x

32.89 = (1 – 0.85) X

32.89 = 0.15X

X = 32.89/0.15

X= 219.27

1 dollar = 100 cents

Hence, $219.27 = 219.27 × 100 cents equal to 21,927 cents

To learn more about interest, click here:

https://brainly.com/question/15089941

#SPJ4

The minimum value and median are used in the five-number summary.

A box and whisker plot displays a "box" with its left edge at Q₁, right edge at Q₃, "center" at Q₂ (the median), and "whiskers" at the maximum and minimum.

Given:

A five-number summary.

That means minimum value, lower quartile (Q1), median value (Q2), upper quartile (Q3), and maximum value.

From the given choices:

The minimum value and median are the required measures.

Therefore, the minimum value and median are the required measures.

To learn more about the box-and-whisker plot ;

https://brainly.com/question/2742784

#SPJ1

Taylor series is \(f(x) = ln2 + \sum_{n=1)^{\infty}(-1)^{n-1} \frac{(n-1)!}{n!(9)^{n}(x9)^{2} }\)

To find the Taylor series for f(x) = ln(x) centering at 9, we need to observe the pattern for the first four derivatives of f(x). From there, we can create a general equation for f(n). Starting with f(x), we have

f(x) = ln(x)

\(f^{1}(x)= \frac{1}{x} \\f^{2}(x)= -\frac{1}{x^{2} }\\f^{3}(x)= -\frac{2}{x^{3} }\\f^{4}(x)= \frac{-6}{x^{4} }\)

.

.

.

Since we need to have it centered at 9, we must take the value of f(9), and so on.

f(9) = ln(9)

\(f^{1}(9)= \frac{1}{9} \\f^{2}(9)= -\frac{1}{9^{2} }\\f^{3}(x)= -\frac{1(2)}{9^{3} }\\f^{4}(x)= \frac{-1(2)(3)}{9^{4} }\)

.

.

.

Following the pattern, we can see that for \(f^{n}(x)\),

\(f^{n}(x)=(-1)^{n-1}\frac{1.2.3.4.5...........(n-1)}{9^{n} } \\f^{n}(x)=(-1)^{n-1}\frac{(n-1)!}{9^{n}}\)

This applies for n ≥ 1, Expressing f(x) in summation, we have

\(\sum_{n=0}^{\infinite} \frac{f^{n}(9) }{n!} (x-9)^{2}\)

Combining ln2 with the rest of series, we have

\(f(x) = ln2 + \sum_{n=1)^{\infty}(-1)^{n-1} \frac{(n-1)!}{n!(9)^{n}(x9)^{2} }\)

Taylor series is \(f(x) = ln2 + \sum_{n=1)^{\infty}(-1)^{n-1} \frac{(n-1)!}{n!(9)^{n}(x9)^{2} }\)

Find out more information about taylor series here

brainly.com/question/13057266

#SPJ4

Answer:

r1/r2 = 2ω2/ω1

Step-by-step explanation:

The velocity of each pulley is expressed as v = ωr where;

v is the linear velocity of the pulley

ω is the angular velocity of the pulley

r is the radius of the pulley.

For the two pulleys, the velocity I'd both pulleys are the same.

v1 = v2

v1 is the linear velocity of first pulley

v2 is the linear velocity of the second pulley.

v1 = ω1r1

v2 = 2ω2(r2)

r1 and r2 is the radius of pulley 1 and pulley 2 respectively.

Since v1 = v2

ω1r1 = 2ω2(r2)

Divide both sides by r2

ω1r1/r2 = 2ω2(r2)/r2

ω1r1/r2 = 2ω2

Divide both sides by ω1

ω1r1/r2/ω1= 2ω2/ω1

r1/r2 = 2ω2/ω1

The Solution using two methods are 323, .291, the correct option is B`.

Probability of an event is a measurement of how likely an event can occur as an outcome of a random experiment.

Probability ranges from 0 to 1, both inclusive. Events whose probability is closer to 0 are rarer to occur than those whose probabilities are closer to 1 (relatively).

When converted to percentage, we just need to multiply its decimal representation by 100. In percentage form, the probability ranges from 0% to 100%.

Given;

Frank is a champion fish charmer who can charm fish with .62 probability of success

He attempts to charm 100 fish, what's the probability he'll charm

between 60 and 80 inclusive

Now, probability out of 100

=62

This is between 60 and 80

So, 323

Therefore, the probability will be 323 and .291

Learn more about interpretation of probability here:

https://brainly.com/question/23024246

#SPJ1

Answer:

\(height = \frac{24}{2} = 12 \: cm \\ adjacent = \frac{32}{2} = 16 \: cm\)

We get a triangle of height 12 cm and adjacent 16 cm

\(side = \sqrt{ {12}^{2} + {16}^{2} } \\ = \sqrt{400} \\ = 20 \: cm\)

Answer:

side=√(24/2)²+(32/2)²

=√12²+16²

=√400

= 20

Answer:

sorry i can't clear

The horizontal asymptote of function f(x) is y=6.5, which is a straight line, which means that even if time is infinite, the pH of the mouth will not rise above 6.5, which is the normal pH of the mouth.

A function's horizontal asymptote is a horizontal line with which the function's graph appears to coincide but does not actually coincide. The horizontal asymptote is used to determine the behavior of the function.

When either lim x f(x) = k or lim x - f(x) = k, the horizontal asymptote of a function y = f(x) is a line y = k. . It is commonly abbreviated as HA. In this case, k is a real number that the function approaches when x is extremely large or extremely small.However, the maximum number of asymptotes that a function can have is 2.

Given,

\(f(x)=\frac{6.5x^2-89.4x+3734}{x^2+576}\)

The horizontal asymptote of the function f(x) can be determined by

\(y=\lim_{x \to \infty} f(x)\\\\=\lim_{x \to \infty}\frac{6.5x^2-89.4x+3734}{x^2+576}\\\\=\lim_{x \to \infty}\frac{x^2(6.5-\frac{89.4}{x}+\frac{3734}{x^2})}{x^2(1+\frac{576}{x^2})}\\\\=\lim_{x \to \infty}\frac{(6.5-\frac{89.4}{x}+\frac{3734}{x^2})}{(1+\frac{576}{x^2})}\\\\=\frac{(6.5-\frac{89.4}{ \infty}+\frac{3734}{ \infty})}{(1+\frac{576}{ \infty})}\\\\=\frac{6.5-0+0}{1+0}\\\\=\frac{6.5}{1}=6.5\)

Thus, the horizontal asymptote of function f(x) is y=6.5 which is straight line which means even the time reaches infinity the pH of mouth will not increase more than 6.5, which is the normal pH of mouth.

To learn more about horizontal asymptote refer here

https://brainly.com/question/4084552

#SPJ4

Your question is incomplete, here is the complete question.

The function \(f(x)=\frac{6.5x^2-89.4x+3734}{x^2+576}\) models the pH level f(x) of a mouth x minutes after eating food containing sugar. The graph of this function is shown.

What is the equation is the horizontal asymptote associated with is function? Describe what this means in terms of mouth's pH level over time.

Answer:

31

Step-by-step explanation:

Square both sides of the equation to get

x+5 = 36

x = 31

1. An event that is likely to happen, but not certain, for the number Kenisha calls is that it is a prime number. While there are several prime numbers between 1 and 75, it is not guaranteed that the number she calls will be prime. However, given the range of numbers, the probability of calling a prime number is relatively high.

2. An event that is unlikely to happen, but not impossible, for the number Kenisha calls is that it is a perfect square. Perfect squares are numbers that can be expressed as the square of an integer. In the range of 1 to 75, there are only a few perfect squares, so the chances of calling one as the bingo number are relatively low, but not impossible.

3. An event that is certain to happen for the number Kenisha calls is that it will be an integer. Since the game is played with whole numbers from 1 to 75, the number called will always be an integer, as it represents a specific whole number in the given range.

\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)

♥️ \(\large{\textcolor{red}{\underline{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)

The solution is given below.

1. An event that is likely to happen, but not certain, for the number Kenisha calls is that it will be an odd number. Since there are 75 numbers in total and half of them are odd, there is a higher probability that the number called will be odd.

2. An event that is unlikely to happen, but not impossible, for the number Kenisha calls is that it will be a perfect square. There are only a few perfect square numbers between 1 and 75, so the chances of calling a perfect square number are lower compared to other numbers.

3. An event that is certain to happen for the number Kenisha calls is that it will be a number between 1 and 75. Since the numbers in the game range from 1 to 75, any number called by Kenisha will definitely fall within this range.

To learn more on probability click:

brainly.com/question/11234923

#SPJ1

Answer:

Graph in pic

Step-by-step explanation:

Graph the parabola using the direction, vertex, focus, and axis of symmetry. Direction: Opens Up

Vertex:  ( 2 , − 7 ) ( 2 , - 7 ) Focus:  ( 2 , \(-\frac{55}{8}\))

Axis of Symmetry:  x = 2

Directrix:  y =  \(-\frac{57}{8}\)

(Hope this helps can i pls have brainlist (crown)☺️)

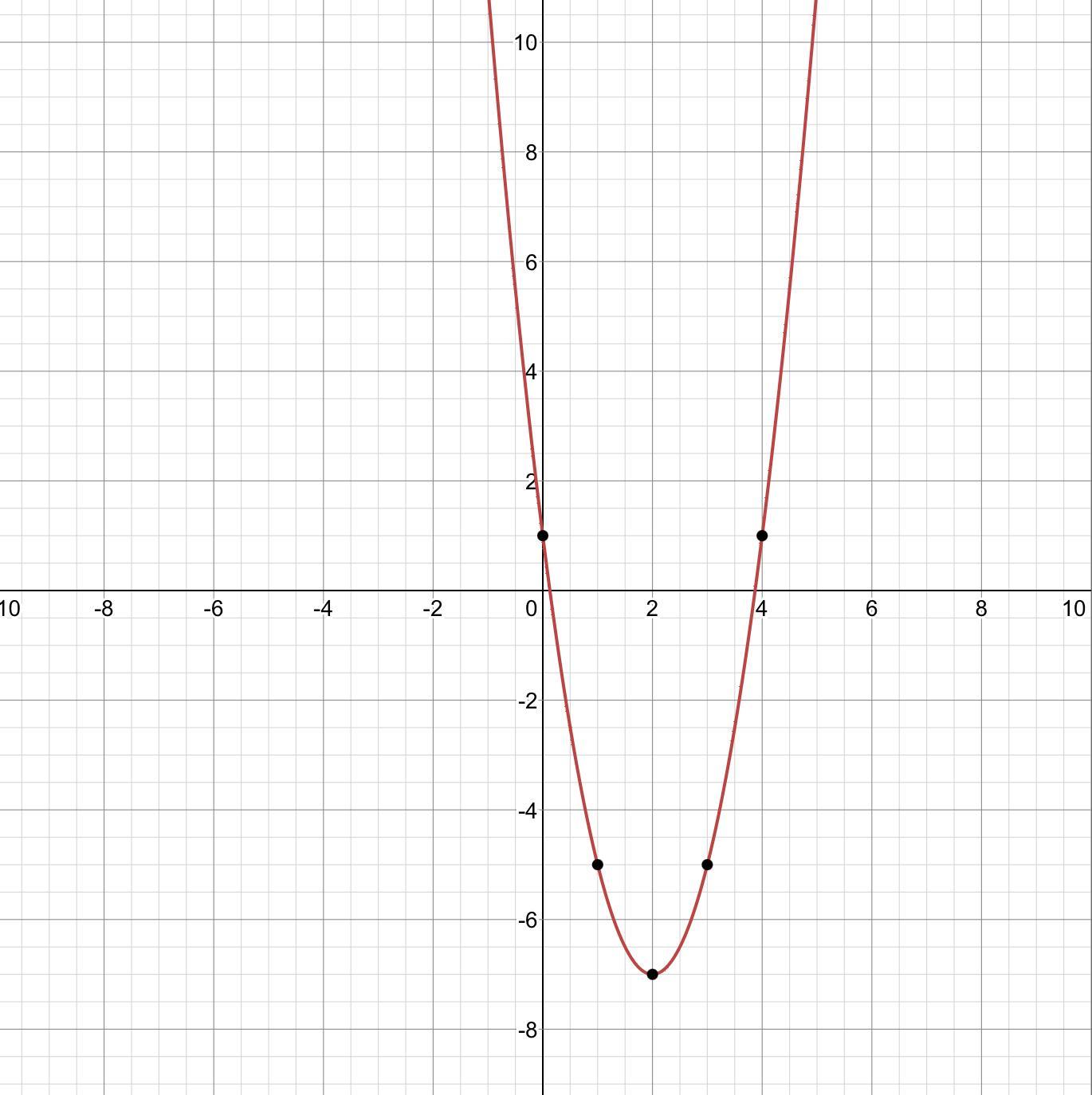
Answer:

(2, --7).

step by step explanation

f(x) =2x^2 -8x+1

We have to put the equation into vertex form by completing the square.

f(x)=2[x-2)^2-7/2]

f(x)=2(x-2*^2-7

The vertex is at

(2,-7)

Check using the graph:

graph{2x^2-8x+1 [-10, 10, -7.76, 2.24]

mark me brainly !!!