what are the numbers for pie I need to know
Answers
Answer:
Pi is exactly \(3.1415926535897932384626433832795\)
Pi is often used in mathematical expressions, calculating measurements, and finding circumference as well as volume.
Related Questions
need help in this and show work

Answers
After answering the given query, we can state that The Pythagorean formula can also be used to determine the cone's cut-off end's diameter: d = (r2 - y2)/2 = (7.2 - 0.6)/2 = 14.27 inches (approximately)
what is a cone?An item with a level base and a smooth, tapering tip or vertex is referred to as a cone in three dimensions. A cone is formed by joining a succession of line segments, half-lines, or lines that link every point on the base in a plane without vertices. A cone is a three-dimensional construction with a smooth shift from a flat, usually circular base to the vertex or peak, which acts as the base's center's axis. An apparent three-dimensional geometric form with a vertically smoothed curved surface is called a cone.
x/h equals (r + y)/r
(r - (h - x - 3)) = (r - (h - x - 3)) = x/h/r
x = r - y = r - (h - x - 3)
x = (2r - h + 3)/2
V = (1/3)πr^2h
2,034.72 = (1/3)πr^2h
2,034.72 = (1/3)πr^2(h - x - 3)
2,034.72 = (1/3)πr^2(h - ((2r - h + 3)/2) - 3)
After simplifying and finding "r," we arrive at:
7.2 centimeters is r.
The height of the removed portion can now be determined using the calculation for "x":
Inches are equal to x = (2r - h + 3)/2 = (2(7.2) - 24 + 3)/2 = 0.6
The Pythagorean formula can also be used to determine the cone's cut-off end's diameter:
d = (r2 - y2)/2 = (7.2 - 0.6)/2 = 14.27 inches (approximately)
To know more about cone visit:
https://brainly.com/question/16394302
#SPJ1
Find the total surface area of this prism where the cross section is an isosceles triangle.
Answers
To get the total surface area: 120 + 260 + 240 = 620 cm^2
What is triangle?In Euclidean geometry, any three points that are not collinear produce a singular triangle and a singular plane (i.e. a two-dimensional Euclidean space). In other words, every triangle is contained in a plane, and there is only one plane that contains that triangle.
All triangles are contained in a single plane if all geometry is on the Euclidean plane, but in higher-dimensional Euclidean spaces, this is no longer the case.
The definition of the terminology used to classify triangles can be found on the first page of Euclid's Elements, which dates back more than two thousand years. In modern classification, names are either directly transliterated from Euclid's Greek or translated from Latin.
According to our question-
(24 × 5) ÷ 2
120 ÷ 2 = 60 cm^2
Since there are two triangles:
60 × 2 = 120 cm^2
Dimensions of two similar rectangles:
The two short lines, which indicate that this is an isosceles triangle, show that they are identical. Both of their sides are the same.
A = L × W
Substitute
10 × 13 = 130
Considering there are two:
130 × 2 = 260 cm^2
Dimensions of the rectangle at bottom:
- Don't overlook the rectangle that forms the base of this shape.
A = L × W
Substitute
24 × 10 = 240 cm^2
To determine the overall surface area, add all of these together:
120 + 260 + 240 = 620 cm^2
Hence, To get the total surface area: 120 + 260 + 240 = 620 cm^2
learn more about triangle click here:
brainly.com/question/1058720
#SPJ4
If teens have about 80h a month of leisure time, how much time would they spend each activity a month?
Answers
Answer:
depends on how many actives there are and maybe on if they preferred one over another it would get more time
Step-by-step explanation:
the ratio 18:24 in its simpilist form
Answers
Answer:
3:4
Step-by-step explanation:
18:24 —> 9:12–> 3:4
hope this helps :)
172 students went on a field trip. seven buses were filled and 25 students traveled in cars. how many students were in each bus? i need an equation with the steps
Answers
The number of students in each bus is 21
Given data
Total number of students on the trip = 172
25 students traveled in cars
7 buses were filled
let the number students on each bus be x
number of students on the bus is gotten by
172 - 25 = 147
so 147 students travelled by bus and the total number of buses is 7.
to get the number of students in each bus we solve as follows
147 / 7 = 21
Hence each bus contains 21 students.
Read more on word problems here: https://brainly.com/question/21405634
#SPJ1
At what depth is there only 1% of surface sunlight

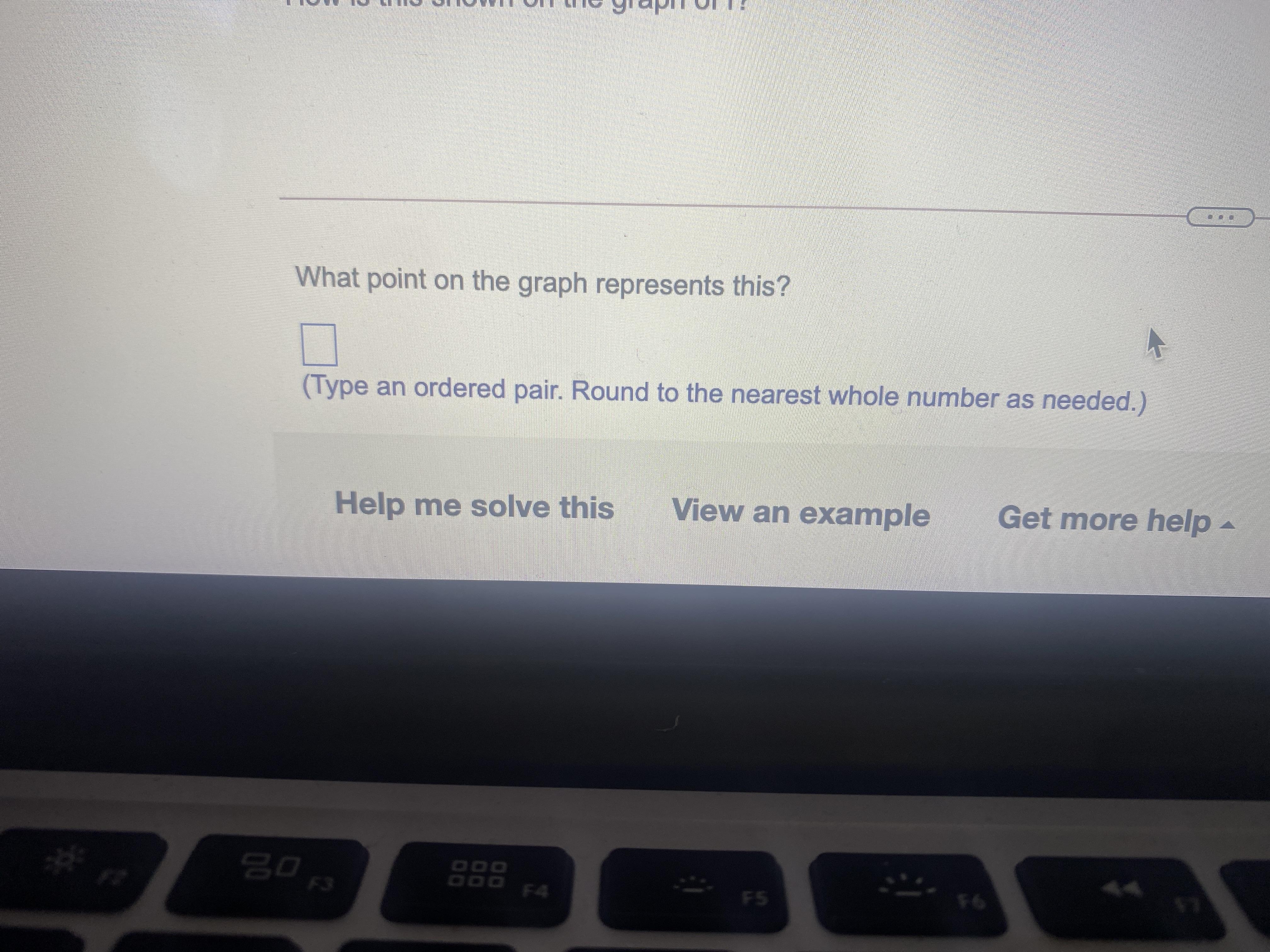
Answers
ANSWER
• 60 feet
,• The point is ,(60, 1)
EXPLANATION
As said, x is depth in feet, and f(x) represents the percentage of surface sunlight that reaches a depth of x feet. We have to find the value of x for which f(x) = 1,
\(1=16(0.955)^x\)Divide both sides by 16,
\(\frac{1}{16}=0.955^x\)Take logarithm to both sides to apply the rule of the logarithm of power on the right side,
\(\log (1/16)=x\log (0.955)\)Divide both sides by log(0.955),
\(x=\frac{\log (\frac{1}{16})}{\log (0.955)}\approx60ft\)In the graph this is,

Question 3(Multiple Choice Worth 2 points)
(Laws of Exponents with Whole Number Exponents MC)
Evaluate
0₁1
16
01
16
32
Question 1 (Answered)

Answers
The answer to the indices is 1/16. Option C
What is an indices?You should understand that in mathematics and computer programming, index notation is used to specify the elements of an array of numbers. The formalism of how indices are used varies according to the subject, depending on whether one is writing a formal mathematical paper for publication, or when one is writing a computer program
The given question is
[(1/4)⁷ ÷ (1/4)⁶]⁷
⇒[ 1/16384 ÷ 1/4096]²
Simplifying this to have
1/16384 * 4096/1
This implies 4096/16384
⇒ 0.25
Converting this to a fraction we divide by 100 to have
0.25/100 = 25/100
Dividing by 25 to have [1/4]²
Therefore the answer is 1/16
Learn more about indices on https://brainly.com/question/30544294
#SPJ1
Identify each system as linear-quadratic or quadratic-quadratic. Then solve.
y=x-1
x²+y²=25
Answers
The solutions to the given system are (4, 3) and (-3, -4).
The given system is,
y = x-1
x²+y² =25
The first equation,
y = x - 1, is a linear-quadratic system.
Substituting y = x - 1 into the second equation, we get:
x² + (x - 1)² = 25
Simplifying this equation, we get:
2x² - 2x - 24 = 0
Dividing by 2, we get:
x² - x - 12 = 0
Factoring this equation, we get:
(x - 4)(x + 3) = 0
So the solutions for x are x = 4 and x = -3.
Substituting these values back into the first equation, we get:
When x = 4, y = 3. When x = -3, y = -4.
Therefore, the solutions to the system are (4, 3) and (-3, -4).
Learn more about system of equations at:
brainly.com/question/14323743
#SPJ4
Mr. Lopez wrote the equation 32 g + 8 g minus 10 g = 150 on the board. Four students explained how to solve for g.
Alyssa: “I added 32 and 8 to get 40, subtracted 10 to get 30, and then subtracted 30 from 150 to find the value of g, which is 120.”
Rahul: “I added 32, 8, and 10 to get 50, and then I subtracted 150 to find the value of g, which is –100.”
Toni: “I subtracted 18 from 32 to get 14, which I then divided into 150 to find the value of g, which is 10 and StartFraction 5 Over 7 EndFraction.”
Wilhem: “I added 32 and 8 to get 40, subtracted 10 to get 30, and then divided both sides by 30 to find the value of g, which is 5.”
Which student’s work is correct?
A. Alyssa
B. Rahul
C. Toni
D. Wilhem
Answers
Answer:
D Wilhem
Step-by-step explanation:
When solving a algebraic equation You follow these steps: group like factors(adding the 32g+8g-10g=30g) then you divide the numbers.(30g=150, 30/30=0 and the 150/30=5) So(g=5)
Answer:
D: Wilhem
Step-by-step explanation:

Please help due today

Answers
3(5)=15
3(2)=6
15+6=21
Answer:
see attached file
Step-by-step explanation:

Select 3 ratios that are = to 11:1
Answers
Hope this helps
you have 0.200 mol of a compound in a 0.720 M solution, what is the volume (in L) of the solution? Question 3 1 pts What is the molarity of a solution that has 1.75 mol of sucrose in a total of 3.25 L of solution? Question 4 1 pts What is the molarity of a solution with 43.7 g of glucose (molar mass: 180.16 g/mol) dissolved in water to a total volume of 450.0 mL?
Answers
For the first question, with 0.200 mol of a compound in a 0.720 M solution, the volume of the solution is approximately 0.278 L. For the second and third questions, the molarities are approximately 0.538 M.
Question 3:
To find the volume (in liters) of a 0.720 M solution containing 0.200 mol of a compound, you can use the formula:
Molarity (M) = moles (mol) / volume (L)
0.720 M = 0.200 mol / volume (L)
Rearranging the formula, we get:
volume (L) = moles (mol) / Molarity (M)
volume (L) = 0.200 mol / 0.720 M
volume (L) ≈ 0.278 L
Therefore, the volume of the solution is approximately 0.278 L.
Question 4:
To find the molarity of a solution with 1.75 mol of sucrose in a total volume of 3.25 L, we can use the formula:
Molarity (M) = moles (mol) / volume (L)
Molarity (M) = 1.75 mol / 3.25 L
Molarity (M) ≈ 0.538 M
Therefore, the molarity of the solution is approximately 0.538 M.
For the third question, the molarity of the solution can be found using the formula:
Molarity (M) = moles (mol) / volume (L)
First, we need to convert the mass of glucose from grams to moles:
moles of glucose = mass of glucose (g) / molar mass of glucose (g/mol)
moles of glucose = 43.7 g / 180.16 g/mol
moles of glucose ≈ 0.242 mol
Now, we can find the molarity of the solution:
Molarity (M) = 0.242 mol / 0.450 L
Molarity (M) ≈ 0.538 M
Therefore, the molarity of the solution is approximately 0.538 M.
To learn more about molarity visit:
https://brainly.com/question/30404105
#SPJ11
4.5k>18 Graph the solution of the inequality.

Answers
Graph the solution of the inequality 4.5k>18 is equal to k > 4 ( see image), by using the inequality equation.
Based on the given conditions,
4.5k>18
What is an Inequality :In mathematics, a relationship between two expressions or values that are not equal to each other is called 'inequality.
The graph of an inequality in two variables is the set of points that represents all solutions to the inequality. A linear inequality divides the coordinate plane into two halves by a boundary line where one half represents the solutions of the inequality.
An inequality compares two values, showing if one is less than, greater than, or simply not equal to another value.
a ≠ b says that a is not equal to b
a < b says that a is less than b
a > b says that a is greater than b
(those two are known as strict inequality)
a ≤ b means that a is less than or equal to b
a ≥ b means that a is greater than or equal to b.
To solve given graph,
We can write,
4.5k>18
4.5k - 18 > 0
4.5k > 18
k > 18/4.5
We can get the division,
k > 4 (We can see image)
Therefore,
4.5k>18 Graph the solution of the inequality is k > 4 ( see image ), by using inequality equation.
To learn more about information visit Inequality :
brainly.com/question/14301369
#SPJ1

identify the slope and y intercept of the function y = - 8x + 1
Answers
Answer:
Slope: -8
Y intercept: (0,1)
Step-by-step explanation:
^^^^
Answer:
\(\star\mathtt{Ans.\:\#1:\:Slope:-8}\)
\(\star\mathtt{Ans.\:\#2:\:y\:intercept:\:1}\)
Step-by-step explanation:
Hi student, let me help you out.
................................................................................................................
First note that the equation we are working with is in slope intercept form. Do you remember the slope intercept form equation? It's \(\mathtt{y=mx+b}\).
In the slope intercept form equation, "m" denotes "slope" and "b" denotes "y intercept".
Looking back at our equation, let's work out the slope & y intercept.
Let's put these two equations together:
\(\mathtt{y=mx+b}\)
\(\mathtt{y=-8x+1}\)
See what I mean? The y intercept of this equation is 1 and the slope is -8.
Hope this helped you out! Ask in comments if any queries arise.
Best wishes from "reflect"!
\(\star\bigstar\underline{\overline{\overline{\underline{\textsf{Reach far. Aim high. Dream big.}}}}}\bigstar\star\)
\(\underline{\rule{300}{6}}\)
very briefly, explain if the value in the dominator of the one sample and independent sample t-test is different? if so, what is the difference and why do we use it?
Answers
The t- test test's sizes for samples 1 and 2 are n1 and n2, respectively.
What can you infer from a sample t-test?
The one-sample t-test is a statistical hypothesis test used to determine whether the population mean of an unknown sample is different from a given value.The t-test, also known as the t-statistic or t-distribution, is a popular statistical technique for analyzing differences between the means (averages) of two groups or between the means of one group and a standard value.df for one sample t-test is n-1
where n is sample size
df for independent sample t-test is n1+n2-2
where n1 and n2 are respective sample sizes for sample 1 and sample 2 .
Learn more about t-test
brainly.com/question/15870238
#SPJ4
Ravi has an ant problem at his house, so he asked pest control to come spray to get rid of the ants. The pesticide that the pest control company uses kills ants at a rate of 35.6% per hour. Before spraying, the pest control company determines that Ravi has about 25,000 ants. Write an equation to model the number of ants, A, Ravi will still have after h hours. ________=________*(________)^________ QUESTION 11 How many ants does Ravi still have after 3 hours? Round to the nearest ant. ________ants QUESTION 12 How long will it take until all of Ravi's ants are gone? ________hours
Answers
The equation to model the number of ants, A, Ravi will still have after h hours is: A = 25,000 * (1 - 0.356)^h. This equation represents the initial number of ants, 25,000, multiplied by the decay factor, (1 - 0.356), raised to the power of h, the number of hours that have passed.
To find out how many ants Ravi still has after 3 hours, we can plug in h = 3 into the equation: A = 25,000 * (1 - 0.356)^3 = 25,000 * 0.644^3 = 10,563.91. Round to the nearest ant, Ravi still has 10,564 ants after 3 hours.
To find out how long it will take until all of Ravi's ants are gone, we can set A = 0 and solve for h: 0 = 25,000 * (1 - 0.356)^h. Taking the natural log of both sides and rearranging gives us: ln(0/25,000) = h * ln(1 - 0.356), or h = ln(0/25,000)/ln(1 - 0.356). However, since the natural log of 0 is undefined, we cannot find an exact value for h. This means that it will take an infinitely long time for all of Ravi's ants to be gone.
Learn more about ants
brainly.com/question/30939387
#SPJ11
when cedric walked into a party, two-thirds of those invited had already arrived. six more people arrived just after cedric, bringing the number at the party to of those invited. what was the total number of invited guests?
Answers
When Cedric walked into a party, two-thirds of those invited had already arrived. Six more people arrived just after Cedric, bringing the number at the party to of those invited. The total number of invited guests is 18 by Linear equations
What was the total number of invited guests?
There are different methods of solving the problem, and we will use the following steps to get the solution of the problem: Let the total number of invited guests be x.Let's solve the problem with a step-by-step explanation.
Step 1: At the time Cedric arrived, two-thirds of the guests were already present.Let the number of guests present at the party when Cedric arrived be A. Therefore, A = (2/3)x
Step 2: Six more people arrived after Cedric got there. Therefore, the total number of guests after the six people arrived is A + 6.
Step 3: The total number of guests present was also x, which is the total number of guests invited. Therefore A + 6 = x.
Step 4: Substitute A = (2/3)x from Step 1 into A + 6 = x from Step 3 to obtain: (2/3)x + 6 = xStep 5: To solve for x, we will get rid of the fraction by multiplying every term by 3x.
Then we will simplify. 3x * (2/3)x + 3x * 6 = 3x * x Simplifying further 2x + 18 = 3x Subtracting 2x from both sides of the equation 18 = x.
For more questions on Linear equations
https://brainly.com/question/26310043
#SPJ11
evaluate the exponent expression for a = –2 and b = 3. question 15 options: a) –9∕8 b) –2∕5 c) –6 d) 3
Answers
The correct option is A) 9∕8, evaluating the exponent expression with a = -2 and b = 3, we find that the value is -8.
We are given the expression a^b, where a = -2 and b = 3. Substituting these values into the expression, we have (-2)^3.
To evaluate this expression, we raise -2 to the power of 3. When we raise a negative number to an odd power, the result will be a negative number.
So, (-2)^3 will yield a negative value.
Calculating (-2)^3, we multiply -2 by itself three times: (-2) × (-2) × (-2). This equals -8.
Therefore, the correct option is A) 9∕8 and the value of the exponent expression (-2)^3 is -8.
To know more about exponent expression refer here:
https://brainly.com/question/9794911#
#SPJ11
Consider the LP below. The BFS ("corners") are (0,0) (0,4) (1,4) (3,2) (3,0). The optimal solution is at x_{1} = 3 and x_{2} = 2
max z = 2x_{1} + x_{2}
s.t.
matrix x 1 +x 2 &<= 0 \\ x 1 &<=3\\ x 2 &<4 matrix
x_{1}, x_{2} >= 0
(a). What is the range of c_{1} the objective coefficient of x_{1} (currently 2) for which this BFS remains optimal:
(b). What is the range of b_{2} the right hand side of the second constraint (currently 3) for which this BFS remains optimal:
(c). What is the dual price of the second constraint?
Answers
(a) The range of c₁ (the objective coefficient of x₁) for which this BFS remains optimal is c₁ ≤ 2.
(b) The range of b₂ (the right-hand side of the second constraint) for which this BFS remains optimal is 3 ≤ b₂ < 4.
(c) The dual price of the second constraint is 0.
(a) The optimality condition for a linear programming problem requires that the objective coefficient of a non-basic variable (here, x₁) should not increase beyond the dual price of the corresponding constraint. In this case, the dual price of the second constraint is 0, indicating that increasing the coefficient of x₁ will not affect the optimality of the basic feasible solution. Therefore, the range of c₁ for which the BFS remains optimal is c₁ ≤ 2.
(b) The range of b₂ for which the BFS remains optimal is determined by the allowable range of the corresponding dual variable. In this case, the dual price of the second constraint is 0, implying that the dual variable associated with that constraint can vary within any range. As long as 3 ≤ b₂ < 4, the dual variable remains within its allowable range, and thus, the BFS remains optimal.
(c) The dual price of a constraint represents the rate of change in the objective function value per unit change in the right-hand side of the constraint, while keeping all other variables fixed. In this case, the dual price of the second constraint is 0, indicating that the objective function value does not change with variations in the right-hand side of that constraint.
Learn more about coefficient
brainly.com/question/1594145
#SPJ11
The football team has played 12 games so far this season they have won 8 games, what percent of their games has the team lost?
plz help I need to know how to set it up
Answers
Answer: They won 80% and lost 20%.
Step-by-step explanation:
which terms can be combined in the polynomial

Answers
Step-by-step explanation:
6x^2, and 9x^2 can both be combined
Which data set COULD NOT be represented by the box plot shown? A) {9, 8, 9, 6, 12, 10, 1 B) {14, 8, 12, 10, 9, 12, 4} C) {4, 9, 8, 11, 10, 12, 14} D) {4, 8, 8, 11, 10, 12, 14}

Answers
Answer:A
Step-by-step explanation:
Do the integral from (-2,2) of the function by Trapezoidal Rule
in Matlab.
1/((25+x^2))^3/2
Answers
Here's how you can use the Trapezoidal Rule to approximate the integral of the function \(f(x) = \frac{1}{{(25+x^2)}^{\frac{3}{2}}}\) from -2 to 2 in MATLAB:
```matlab
a = -2; % Lower limit
b = 2; % Upper limit
n = 1000; % Number of subintervals (increase for higher accuracy)
h = (b - a) / n; % Step size
x = a:h:b; % Generate evenly spaced x values
y = 1 ./ (25 + x.^2).^1.5; % Evaluate the function at x
approximation = h * (sum(y) - (y(1) + y(end)) / 2); % Trapezoidal Rule approximation
fprintf('Approximation: %.6f\n', approximation);
```
1. We define the lower limit `a` as -2, the upper limit `b` as 2, and the number of subintervals `n` as 1000 (you can adjust `n` for higher accuracy).
2. We calculate the step size `h` by dividing the range (`b - a`) by the number of subintervals (`n`).
3. We generate an array `x` of evenly spaced values from `a` to `b` using the step size `h`.
4. We evaluate the function `f(x)` at each point in `x` and store the results in the array `y`.
5. Finally, we use the Trapezoidal Rule formula to approximate the integral by summing the values in `y` and adjusting for the endpoints, multiplying by the step size `h`.
The Trapezoidal Rule approximation for the integral of the function \(f(x) = \frac{1}{{(25+x^2)}^{\frac{3}{2}}}\) from -2 to 2 is the value calculated using the MATLAB code above.
To know more about Trapezoidal Rule follow the link:
https://brainly.com/question/28592530
#SPJ11
Tickets to the local carnival cost $5.50 for adults and $3.00 for children under the age of 12. A group of 8 people bought tickets to the carnival for $36.50. Write a system of equations to represent this scenario. How many adult tickets were sold? Just type in the ONE number answer.
Answers
Answer:
5 adult tickets
Step-by-step explanation:
Let x be adult tickets and y be tickets for children under the age of 12.
We know the group of 8 people spent a total of 36.50 dollars, so we can create the following system of equations:
$5.5x + $3y = $36.5
x + y = 8
Now we can graph this system to help us answer the question.
-> See attached
-> The point at which the lines intersect answers our question. It means these values satisfy both equations.
The equations, when graphed, intersect at point (5, 3). In the beginning I said that x is adult tickets, so 5 adult tickets were sold.

Five adults were in the group of 8.
Step-by-step explanation:\(Let\ x=#\ adult\ tickets\) \(5.5x+3(-x+8)=36.5\)
\(y=#\ child\ tickets\) \(5.5\times-3x+24=36.5\)
\(2.5x=12.5\)
\(x+y=8\rightarrowy=-x+8\) \(\nearrow\) \(x=5\)
\(5.5x+3y=36.5\)
\(5+y=8\)
\(y=3\)
I hope this helps you
:)
a small radio transmitter broadcasts in a 20 mile radius. if you drive along a straight line from a city 27 miles north of the transmitter to a second city 24 miles east of the transmitter, during how much of the drive will you pick up a signal from the transmitter?
Answers
To solve the given problem first we need to find the equation for line then we have to find the intersection point on circle.
You will pick up a signal from the transmitter in 29% of the drive.
Given:
The radius is 53 mile.
The origin point of transmitter is .
Calculate the slope of line with point and .
Substitute the value.
Write the general equation of line.
Now we got the equation of line,
Write the transmitter reach the area enclosed by the next circle.
Substitute the value of .
Further solving we get the point and .Please refer the attached figure.Apply the Pythagoras theorem to find the total distance.Apply the Pythagoras theorem to find distance when the signal is picked up.Calculate the percentage of distance covered.Thus, You will pick up a signal from the transmitter in 29% of the drive.
Learn more about what equation of line is here:
brainly.com/question/21511618
#SPJ4
The sum of the measures of the angles of a triangle is 180 m

Answers
The sum of the measures of the angle of a triangle is 180 degrees.
Sum of angles in a triangleThe given triangle is a type of triangle and the type of triangle a scalene triangle.
For a scalene triangle, the measure of the three sides are unequal and the sum of the interior angle of a triangle is 180 degrees.
Hence the measure of the angles <A, <B and <C are all less than 90 degrees since they are all acute angles.
We can therefore conclude that:
m<A + m<B + m<C = 180 degrees
Learn more on triangle sum theorem here: https://brainly.com/question/30870203
#SPJ1
The half-life of a certain radioactive substance is 45 days. There are 6.2 grams present initially. On what day
will there be less than 1 gram remaining? Day
Answers
Answer:
There will be less than 1 gram of the radioactive substance remaining by the elapsing of 118 days
Step-by-step explanation:
The given parameters are;
The half life of the radioactive substance = 45 days
The mass of the substance initially present = 6.2 grams
The expression for evaluating the half life is given as follows;
\(N(t) = N_0 \left (\dfrac{1}{2} \right )^{\dfrac{t}{t_{1/2}}\)
Where;
N(t) = The amount of the substance left after a given time period = 1 gram
N₀ = The initial amount of the radioactive substance = 6.2 grams
\(t_{1/2}\) = The half life of the radioactive substance = 45 days
Substituting the values gives;
\(1 = 6.2 \left (\dfrac{1}{2} \right )^{\dfrac{t}{45}\)
\(\dfrac{1}{6.2} = \left (\dfrac{1}{2} \right )^{\dfrac{t}{45}\)
\(ln\left (\dfrac{1}{6.2} \right ) = {\dfrac{t}{45} \times ln \left (\dfrac{1}{2} \right )\)
\(t = 45 \times \dfrac{ln\left (\dfrac{1}{6.2} \right ) }{ln \left (\dfrac{1}{2} \right )} \approx 118.45 \ days\)
The time that it takes for the mass of the radioactive substance to remain 1 g ≈ 118.45 days
Therefore, there will be less than 1 gram of the radioactive substance remaining by the elapsing of 118 days.
Find the change in profit P for the given marginal. Assume that the number of units x increases by 5 from the specified value of x. (Round your answer to two decimal places.) Marginal Number of Units, x dP dx = 12.1 60 − 3 x x = 121
Answers
The change in profit (ΔP) when the number of units (Δx) increases by 5, based on the given marginal profit function, is -18331.50
To find the change in profit (ΔP) when the number of units (Δx) increases by 5.
we need to evaluate the marginal profit function and multiply it by Δx.
The marginal profit function is given by dP/dx = 12.1(60 - 3x).
We are given the value of x as 121, so we can substitute it into the marginal profit function to find the marginal profit at that point.
dP/dx = 12.1(60 - 3(121))
= 12.1(60 - 363)
= 12.1(-303)
= -3666.3
Now, we can calculate the change in profit (ΔP) by multiplying the marginal profit by Δx, which is 5 in this case.
ΔP = dP/dx×Δx
= -3666.3 × 5
= -18331.5
To learn more on Change in Profit click:
https://brainly.com/question/31420071
#SPJ4
Find a sinusoidal function with the following four attributes: (1) amplitude is 10, (2) period is 5, (3) midline is y = 31, and (4) ƒ(3) = 41. f(x) = =
Answers
The sinusoidal function that satisfies the given attributes is f(x) = 10 * sin(2π/5 * x - π/5) + 31.
To find a sinusoidal function with the given attributes, we can use the general form of a sinusoidal function:
f(x) = A * sin(Bx + C) + D
where A represents the amplitude, B represents the frequency (related to the period), C represents the phase shift, and D represents the vertical shift.
Amplitude: The given amplitude is 10. So, A = 10.
Period: The given period is 5. The formula for period is P = 2π/B, where P is the period and B is the coefficient of x in the argument of sin. By rearranging the equation, we have B = 2π/P = 2π/5.
Midline: The given midline is y = 31, which represents the vertical shift. So, D = 31.
f(3) = 41: We are given that the function evaluated at x = 3 is 41. Substituting these values into the general form, we have:
41 = 10 * sin(2π/5 * 3 + C) + 31
10 * sin(2π/5 * 3 + C) = 41 - 31
10 * sin(2π/5 * 3 + C) = 10
sin(2π/5 * 3 + C) = 1
To solve for C, we need to find the angle whose sine value is 1. This angle is π/2. So, 2π/5 * 3 + C = π/2.
2π/5 * 3 = π/2 - C
6π/5 = π/2 - C
C = π/2 - 6π/5
Now we have all the values to construct the sinusoidal function:
f(x) = 10 * sin(2π/5 * x + (π/2 - 6π/5)) + 31
Simplifying further:
f(x) = 10 * sin(2π/5 * x - 2π/10) + 31
f(x) = 10 * sin(2π/5 * x - π/5) + 31
Therefore, the sinusoidal function that satisfies the given attributes is f(x) = 10 * sin(2π/5 * x - π/5) + 31.
Learn more about sinusoidal function here
https://brainly.com/question/29529184
#SPJ11
One Baseball Weigh 14.2 g how many grams would 100 baseballs weigh
Answers
Answer:
1,420 grams per 100 baseballs
Step-by-step explanation:
Set up an equation:
Variable x = grams per 100 baseballs
1/14.2 = 100/x
Cross multiply
1 × x = 14.2 × 100
1x = 1420
x = 1420