What are the solutions to the trigonometric equation on the
interval [0,2π)?
2cos2x=cosx
Select all correct solutions.
0
π6
π3
π2
2π3
5π6
π
Answers
All the solutions to the trigonometric equation on the interval [0,2π) are,
⇒ x = π/2 , 3π/2, π/3, 5π/3
We have,
The trigonometry equation is,
2 cos²x = cos x
We can simplify it,
⇒ 2 cos²x = cos x
⇒ 2 cos²x - cos x = 0
⇒ cos x (2 cos x - 1) = 0
This gives,
⇒ cos x = 0
⇒ x = π/2 , 3π/2
⇒ 2 cos x - 1 = 0
⇒ cos x = 1/2
⇒ x = π/3, 5π/3
Therefore, All the solutions to the trigonometric equation on the interval [0,2π) are,
⇒ x = π/2 , 3π/2, π/3, 5π/3
Learn more about trigonometric ratios at:
brainly.com/question/1836193
#SPJ12
Related Questions
1.
A jar contains n nickels and d dimes worth a total of $30. Which equation models this
information?
A. 0.05n +0.10 = 30
B. 5n + 10d = 30
C. 0.50 +0.10 = 30
D. n + d = 30
Answers
The required equation model is n + d = 30 which represents a jar containing n nickels and d dimes worth a total of $30. which is the correct answer would be an option (D).
What is a numerical expression?A numerical expression is algebraic information stated in the form of numbers and variables that are unknown. Information can is used to generate numerical expressions.
We have been given that a jar contains n nickels and d dimes worth a total of $30.
To determine the equation model that represents the given information.
As per the given information, the algebraic form is:
quantity of nickels + quantity of dimes = total worth
n + d = 30
Thus, the required equation model is n + d = 30 which represents a jar containing n nickels and d dimes worth a total of $30.
Hence, the correct answer would be option (D).
To learn more about numerical expression click here :
https://brainly.com/question/6037813
#SPJ6
y2-y1m =X2-X1Find the slope of the line that passesthrough these two points.Simplify completely.(1,5)(4.6)[2]
![y2-y1m =X2-X1Find the slope of the line that passesthrough these two points.Simplify completely.(1,5)(4.6)[2]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/FStwJlkqHgjw5mVGKMe8iKpcH2agB8Ts.jpeg)
Answers
Okay, here we have this:
Considering the provided points and information, we are going to calculate the requested slope, so we obtain the following:
m=(y2-y1)/(x2-x1)
m=(6-5)/(4-1)
m=1/3
Finally we obtain that the slope of the line is 1/3.
please help meeeeeeee

Answers
1. A committee of 3 men and 4 women is to be formed from 5 men and 6 women. If a particular woman is not to be included, how many different committees are possible
Answers
Step-by-step explanation:
Taking the men first: there are 5 ways to form a 4-man committee out of 5 men.
Taking the women now: There are 20 ways to form a 3-woman committee out of 6 women.
Each of the 5 possible male groups can be combined with any of the 20 possible female groups.
So: 100.
evaluate tan(sin^-1)(7/9)
Answers
SOLUTION
Given the question, the following are the steps to solve the problem
Step 1: Write out the question
\(\tan (\sin ^{-1})(\frac{7}{9})\)Step 2: Solve the expression in the first bracket
\(\begin{gathered} \tan (\sin ^{-1})(\frac{7}{9}) \\ (\sin ^{-1})(\frac{7}{9})=51.05755873 \end{gathered}\)Step 3: Calculate the tangent of the result in step 2
\(\begin{gathered} \tan (\sin ^{-1})(\frac{7}{9}) \\ =\tan (51.05755873) \\ =1.237436867 \\ \approx1.2374 \end{gathered}\)Hence, the result from the evaluation of tan(sin^-1)(7/9) is approximately 1.2374
Find the value of x.

Answers
Answer:
x = 12
Step-by-step explanation:
The sum of the exterior angles of a convex polygon is 360°.
(5x +4)° +(4x +9)° +(9x -6)° +(4x +1)° +(7x +4)° = 360°
29x +12 = 360 . . . . . divide by °, collect terms
29x = 348 . . . . . . . subtract 12
x = 12 . . . . . . . . . divide by 29
Answer:
x=11.58
Step-by-step explanation:
The sum of an exterior angle of a polygon is 360°,
9x-6+4x+9+5x+4+7x+4+4x+1=360°
29x+24=360
29x=360-24
29x=336
x=336/29
x= 11.586
x=11.58
Hope it helps! :)
Select the correct answer. malik is baking pumpkin bread and banana bread for friends and family. his pumpkin bread recipe calls for 4 eggs and cups of flour, and his banana bread recipe calls for 1 egg and cups of flour. malik has 14 eggs, 16 cups of flour, and plenty of other ingredients to make multiple loaves. what is one combination of breads malik can bake without getting more ingredients? a. 3 loaves of pumpkin bread and 3 loaves of banana bread b. 1 loaf of pumpkin bread and 9 loaves of banana bread c. 2 loaves of pumpkin bread and 6 loaves of banana bread d. 5 loaves of pumpkin bread and 1 loaf of banana bread
Answers
The correct answer is
2 loaves of pumpkin bread and 6 loaves of banana bread. Option C.
How to find a possible combination of bread?For the solution for the Pumpkin bread:
4 eggs
3 1/2 cups of flour
Banana bread:
1 egg
1 (0.5) cups of flour
Available ingredients:
14 eggs
16 cups of flour
Assume 2 loaves of pumpkin bread and 6 loaves of banana bread
For the solution for the Pumpkin bread:
PB=4 eggs* 2
PB= 8 eggs
PB=3 *0.5 * 2
PB = 7 cups of flour
For the solution of the Banana bread:
BB =1 *6
BB= 6 eggs
For cups
BB= 1 (0.5) * 6
BB= 9 cups of flour
In conclusion, The solution of the Total used ingredients
I=8 + 6
I= 14 eggs
For cups
IC=7 + 9
IC= 16 cups of flour
Read more about ingredients:
https://brainly.com/question/26532763
#SPJ1
Answer:
C 2 loaves of Pb and 6 loaves of BB
Step-by-step explanation:
For the linear regression y = ẞ1 + ẞ2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 +681 +382 + 18ẞ1ẞ2
Derive the partial derivatives of SSE with respect to B1 and B2 and solve the optimal values of these parameters.
a. B₁ = B1
b. B₂ =
Answers
The optimal values of these parameters are:
a. β₁ = 0
b. β₂ = 0
The linear regression y = β1 + β2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 + 681 + 382 + 18β1β2
Derive the partial derivatives of SSE with respect to β1 and β2 and solve the optimal values of these parameters.
Given that SSE = 382 + 681 + 382 + 18β1β2 ∂SSE/∂β1 = 0 ∂SSE/∂β2 = 0
Now, we need to find the partial derivative of SSE with respect to β1.
∂SSE/∂β1 = 0 + 0 + 0 + 18β2 ⇒ 18β2 = 0 ⇒ β2 = 0
Therefore, we obtain the optimal value of β2 as 0.
Now, we need to find the partial derivative of SSE with respect to β2. ∂SSE/∂β2 = 0 + 0 + 0 + 18β1 ⇒ 18β1 = 0 ⇒ β1 = 0
Therefore, we obtain the optimal value of β1 as 0. Hence, the partial derivative of SSE with respect to β1 is 18β2 and the partial derivative of SSE with respect to β2 is 18β1.
Thus, the optimal values of β1 and β2 are 0 and 0, respectively.
Therefore, the answers are: a. β₁ = 0 b. β₂ = 0
Learn more about regression analysis at
https://brainly.com/question/31691955
#SPJ11
Given that f(x)=x-5 g(x)=5x and h(x)=-f(x+1)-3g(x-1), then what is the value of h(3)?
please show step by step answer.
Answers
Answer:
Step-by-step explanation:
f(x) = x - 5 and g(x) = 5x
- f(x + 1) = - ( x + 1 - 5 ) = 4 - x
- 3g(x - 1 ) = - 3 [ 5 (x - 1)] = 15 - 15x
h(x) = 4 - x + 15 - 15x = 19 - 16x
h(3) = 19 - 16(3) = - 29
Find the area of the region which is inside the polar curve r=5sin(θ) but outside r=4. Round your answer to four decimal places
Answers
The area of the region which is inside the polar curve r = 5 sinθ but outside r = 4 will be 3.75 square units.
What is an area bounded by the curve?When the two curves intersect then they bound the region is known as the area bounded by the curve.
The area of the region which is inside the polar curve r = 5 sinθ but outside r = 4 will be
Then the intersection point will be given as
\(\rm 5 \sin \theta = 4\\\\\theta = 0.927 , 2.214\)
Then by the integration, we have
\(\rightarrow \dfrac{1}{2} \times \int _{0.927}^{2.214}[ (5 \sin \theta)^2 - 4^2] d\theta \\\\\\\rightarrow \dfrac{1}{2} \times \int _{0.927}^{2.214} [25\sin ^2 \theta - 16] d\theta \\\\\\\rightarrow \dfrac{1}{2} \times \int _{0.927}^{2.214} [ \dfrac{25}{2}(1 - \cos 2\theta ) - 16] d\theta \\\)
\(\rightarrow \dfrac{1}{2} [\dfrac{25 \theta }{5} - \dfrac{25 \cos 2\theta }{2} - 16\theta]_{0.927}^{2.214} \\\\\\\rightarrow \dfrac{1}{2} [\dfrac{25(2.214 - 0.927) }{5} - \dfrac{25 (\cos 2\times 2.214 - \cos 2\times 0.927) }{2} - 16(2.214 - 0.927]\\\)
On solving, we have
\(\rightarrow \dfrac{1}{2} \times 7.499\\\\\rightarrow 3.75\)
Thus, the area of the region is 3.75 square units.
More about the area bounded by the curve link is given below.
https://brainly.com/question/24563834
#SPJ4
Every student at a music college learns the flute, the violin, or both the flute and the violin. of the students who learn the flute also learn the violin. 3 times as many students learn the violin as learn the flute. x students learn both the flute and the violin. Find an expression, in terms of x, for the total number of students at the college. Flute X Violin
Answers
The total number of students in the college is expressed as: 5x
How to solve Algebra Word Problems?The parameters given are:
1/2 of the students who learn the flute also learn the violin.
3 times as many students learn the violin as learn the flute.
x students learn both the flute and the violin
Thus, the total who learn the flute = 2x
Number who learn only flute = x
Since 3 times as many students learn the violin as learn the flute. Then, 3x students only learn the violin.
Thus, total number of students at the college is:
x + x + 3x = 5x
Read more about Algebra Word Problems at: https://brainly.com/question/4344214
#SPJ1
Complete question is:
Every student at a music college learns the flute, the violin, or both the flute and the violin. 1/2 of the students who learn the flute also learn the violin. 3 times as many students learn the violin as learn the flute. x students learn both the flute and the violin. Find an expression, in terms of x, for the total number of students at the college. Flute X Violin
Graph 4x + y = 3 help

Answers
A graph of the linear equation y = -4x + 3 in slope-intercept form is shown in the image attached below.
What is a graph?In Mathematics, a graph can be defined as a type of chart that is typically used for the graphical representation of data points or ordered pairs on both the horizontal and vertical lines of a cartesian coordinate, which are the x-axis and y-axis respectively.
First of all, we would rewrite the linear function in slope-intercept form by making y the subject of formula as follows;
4x + y = 3
y = -4x + 3
Next, we would use an online graphing calculator to plot the given linear function as shown in the graph attached below.
In conclusion, the slope of this linear function is equal to -4 and it does not represent a proportional relationship.
Read more on a graph here: brainly.com/question/4546414
#SPJ1

-5+v=4 please help me I beg of you
Answers
Answer:
v = 9
Step-by-step explanation:
-5 + v = 4
+5 +5
-------------------
v = 9
To check just plug 9 in for v.
-5 + 9 = 4
PLEASSSE help will give brainliest

Answers
Answer:
c
Step-by-step explanation:
you divide each side by four to get a=2.5 b=2.5 and c=3
Answer:
The answer is C.
Step-by-step explanation:
If this does not help you im sorry!
Have a good day!
What equation is log10 equal to?
a) (b + 4r = 7)
b) ( p- (7q + 1/2 r)
c) (x / y^2 √z)
Help me! Do not do incorrect answering.
This is super urgent!
Answers
Answer: C
The equation (b + 4r = 7) is a missing number equation, not representing log10. The equation (p- (7q + 1/2 r) would be correct, if the 7q were a 2q. The answer to the question would have to be C, (x / y^2 √z).
Hope this helps you!
May I please receive help?
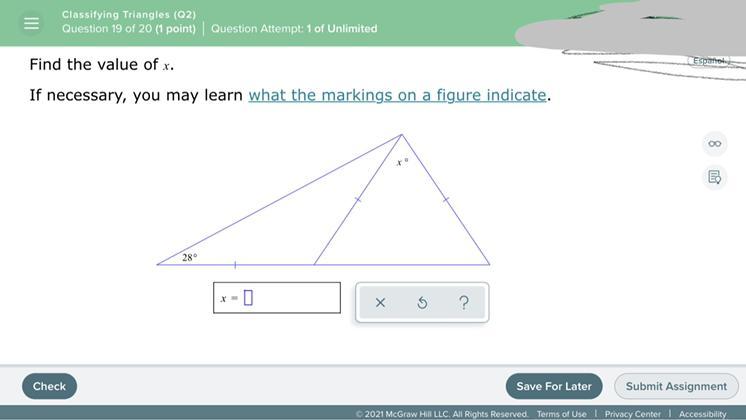
Answers
Answer:
68
Step-by-step explanation:
Hey your so polite and it’s appreciated! First mark other side of angle (right) as 28. 180-56 = 124. Since other side is smaller don’t make it equal. So it has to be higher than 61. So it’s 68! hope this helps !
Which ordered pair? (Picture Included)

Answers
Answer:
(1,9)
Step-by-step explanation:
For a function, each x value has only one y value. 2, 3, and 4 are already used up.
(1,9)
Answer:
(1, 9)
Step-by-step explanation:
(1, 9) is the only possible answer,because the others have the same domain above the question, so they can't be a function
_____ compare one quantity to 100.
A. Factors
B. Variables
C. Percents
D. Interest rates
Answers
Answer:
c
Step-by-step explanation:
PLEASE HELP ASSP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
r = 8.2
Step-by-step explanation:
5r – 10 = –51
5r = –41
r = 8.2
An indoor water park has two giant buckets that slowly fill with 1000 gallons of water before dumping it on the people below. One bucket dumps water every 18 minutes. The other bucket dumps water every 16 minutes. It is currently 2:45 P.M. And both buckets dumped water 15 minutes ago. Find the next two times that both buckets dump water at the same time.
Answers
Answer:
The next two times both buckets dump water at the same time are 4:54 P.M and 7:18 P.M.
Step-by-step explanation:
From the question, one bucket dumps water every 18 minutes, say bucket A;
and the other bucket dumps water every 16 minutes, say bucket B.
Also, It is currently 2:45 P.M. and both buckets dumped water 15 minutes ago,
that is, both buckets dumped water at 2:30 P.M.
For bucket A, the next times it will dump water will be:
2:48 P.M, 3:06 P.M, 3:24 P.M, 3:42 P.M, 4:00 P.M, 4:18 P.M, 4:36 P.M, 4:54 P.M, 5:12 P.M, 5:30 P.M, 5:48 P.M, 6:06 P.M, 6:24 P.M, 6:42 P.M, 7:00 P.M, 7:18 P.M, 7:36 P.M, 7:54 P.M, 8:12 P.M, 8:30 P.M etc.
For bucket B, the next times it will dump water will be:
2:46 P.M, 3:02 P.M, 3:18 P.M, 3:34 P.M, 3:50 P.M, 4:06 P.M, 4:22 P.M, 4:38 P.M, 4:54 P.M, 5:10 P.M, 5:26 P.M, 5:42 P.M, 5:58 P.M, 6:14 P.M, 6:30 P.M, 6:46 P.M, 7:02 P.M, 7:18 P.M, 7:34 P.M, 7:50 P.M etc.
From above, we observe that the next two times both buckets dump water at the same time are 4:54 P.M and 7:18 P.M.
Hence, the next two times both buckets dump water at the same time are 4:54 P.M and 7:18 P.M.
plsss help with image below

Answers
An equation for the boiling point of this liquid is y = -0.0015x + 215.55. Also, the boiling point of this liquid at 2500 ft is equal to 211.8°F.
How to write an equation for the boiling point of this liquid?In order to write an equation for the boiling point of this liquid, we would have to first calculate its slope because the relationship between altitude and the boiling point of this liquid is linear (direct proportion or proportional relationship).
Mathematically, the slope of any linear equation can be calculated by using this formula;
Slope, m = (Change in y-axis, Δy)/(Change in x-axis, Δx)
Slope, m = (y₂ - y₁)/(x₂ - x₁)
From the information provided about the altitudes and boiling points of this liquid, we have the following parameters:
Point (x, y) = (8500, 202.8)
Point (x, y) = (4200, 206.7)
Substituting the given points into the formula, we have;
Slope, m = (209.25 - 202.8)/(4200 - 8500)
Slope, m = 6.45/-4300
Slope, m = -0.0015
At point (8500, 202.8), the equation of this line is given by:
y - y₁ = m(x - x₁)
Where:
m represents the slope.x and y are the data points.y - 202.8 = -0.0015(x - 8500)
y - 202.8 = -0.0015x + 12.75
y = -0.0015x + 12.75 + 202.8
y = -0.0015x + 215.55
Now, we can calculate the boiling point of this liquid at 2500 ft:
y = -0.0015(2500) + 215.55
y = -3.75 + 215.55
y = 211.8°F.
Read more on slope here: https://brainly.com/question/6843937
#SPJ1
Complete Question:
The relationship between altitude and the boiling point of a liquid is linear. At an altitude of 8500 ft, the liquid boils at 202.8°F. At an altitude of 4200 ft, the liquid boils at 209.25°F. Write an equation giving the boiling point b of the liquid, in degrees Fahrenheit, in terms of altitude a, in feet. What is the boiling point of the liquid at 2500 ft?
-Find the indicated sum.7x3 + 7x²+ 184x34x24x2
Answers
Solution
For this case we can do the following
7x^3 + 7x^2 +18
4x^3 -4x^2 - 4x - 2
_________________
11x^3 +3x^2 -4x +1
write two linear expressions that have a difference of x + 1
Answers
Linear expressions are expressions in which the highest power of the variable is 1.
Linear expressions 3x - 2 and 2x - 3 have a difference of 3x - 2
The given parameter is:
\(\mathbf{difference = x + 1}\)
Let one of the linear expressions be 2x - 3, and the other expression be y.
So, the difference would become
\(\mathbf{y -(2x -3) = x + 1}\)
Open bracket
\(\mathbf{y -2x +3 = x + 1}\)
Collect like terms
\(\mathbf{y = 2x + x + 1 - 3}\)
Evaluate like terms
\(\mathbf{y = 3x - 2}\)
Hence, 3x - 2 and 2x - 3 have a difference of 3x - 2
Read more about linear expressions at:
https://brainly.com/question/7510157
Which equation matches this table?
X 1 2 3 7 8
Y 6 12 18 42 48
A. y = x ÷ 6
B. y, = , x, - 6
C. y = 6x
D. y, = , x, + 6

Answers
Answer:
y=6x
Step-by-step explanation:
if u times x by 6 you get the y number underneath
for example:
x=1
y=6
so 1×6=6
x=2
y=12
so 2×6=12
.Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width.
4x+y^2=12, x=y
Then find the area S of the region.
S=?
Answers
The area of the region enclosed by the curves is (3√3 - 13)/3.
To sketch the region enclosed by the given curves 4x+y^2=12, and x=y, we can begin by graphing the curves.
First, let's graph the curve 4x+y^2=12 by rewriting it in terms of y:
\(y^2 = 12 - 4x\)
This is a parabola that opens to the right and is centered at (3,0), with a width of 2√3.
Next, let's graph the line x=y, which passes through the origin at a 45-degree angle.
The region enclosed by the curves is the shaded region in the figure below:
To find the area of this region, we need to integrate with respect to x or y. Since the curves intersect at x=3, it's convenient to use vertical strips and integrate with respect to x.
The height of each strip is given by the difference between the y-coordinates of the parabola and the line at the corresponding x-value, which is:
y = √(12 - 4x) - x
The width of each strip is dx.
Thus, the area of the region is given by the integral:
S = ∫[0,3] (√(12 - 4x) - x) dx
We can simplify this integral by using the substitution u = 12 - 4x, du/dx = -4:
S = ∫[0,3] (√u - 3 + u/4) (-du/4)
S = ∫[0,12] (√u - 3 + u/4) (-du/4) (by extending the limits of integration)
S = [\(-u^{(3/2)/6} - 3u/4 + u^{2/32\)]_[0,12]
S = (3√3 - 13)/3
For more such questions on curves visit:
https://brainly.com/question/30452445
#SPJ11
Lines l and m intersect so that the measure of ∠1 is 50°. What is the measure of ∠2?
Answers
Answer:
Step-by-step explanation:
Without an illustration, I can’t know the position of ∠2 to ∠1.
If the angles are adjacent then ∠2 = 180° - ∠1 = 130°.
Otherwise, ∠2 = ∠1 = 50°
Question 4: Optimization (25 points) Find the maximum and minimum of the following functions over the indicated interval: f(x)=−2x−1 over [−3,5]f(x)=x3−4x+10 over [−10,10]f(x)=xx2+1 over [1,4] Question 1: Inverse Functions ( 25 points) Find the inverse function of the following functions: - y=7x+4 - y=x−2x+1 - y=ex+5 - y=x3+2 Question 2: Concave/Convex Functions (25 points) Are the following functions convex or concave? Why?: - f(x)=x2−2x+2 - f(x)=5x31 - f(x)=3x3+2x+1 Question 3: Derivative of Functions ( 25 points) Differentiate the following functions with respect to x : - f(x)=6x5−2x15 - f(x)=x−23x−5 - f(x)=x5x+1 - f(x)=(x2+x+1)5ln(x+1)
Answers
The maximum value is 5 and the minimum value is -11.The maximum value is approximately 13.84 and the minimum value is -1040. The maximum value is approximately 0.8 and the minimum value is -0.333.
1. For f(x) = -2x - 1 over [-3, 5]:
- Take the derivative of f(x) with respect to x: f'(x) = -2.
- Set f'(x) equal to zero and solve for x: -2 = 0. There are no solutions, so there are no critical points.
- Since the interval is finite, we evaluate f(x) at the endpoints:
- f(-3) = -2(-3) - 1 = 5.
- f(5) = -2(5) - 1 = -11.
- Therefore, the maximum value is 5 and the minimum value is -11.
2. For f(x) = x³ - 4x + 10 over [-10, 10]:
- Take the derivative of f(x) with respect to x: f'(x) = 3x² - 4.
- Set f'(x) equal to zero and solve for x: 3x² - 4 = 0.
- x = 2/√3 or x = -2/√3.
- Since the interval is finite, we evaluate f(x) at the endpoints and critical points:
- f(-10) = -10³ - 4(-10) + 10 = -1040.
- f(-2/√3) ≈ 8.16.
- f(2/√3) ≈ 13.84.
- f(10) = 10³ - 4(10) + 10 = 960.
- Therefore, the maximum value is approximately 13.84 and the minimum value is -1040.
3. For f(x) = x/(x^2 + 1) over [1, 4]:
- Take the derivative of f(x) with respect to x: f'(x) = (x² + 1 - 2x²) / (x² + 1)².
- Set f'(x) equal to zero and solve for x: (x²+ 1 - 2x²) / (x² + 1)² = 0.
- x² + 1 - 2x² = 0.
- -x² + 1 = 0.
- x² = 1.
- x = ±1.
- Since the interval is finite, we evaluate f(x) at the endpoints and critical points:
- f(1) = 1 / (1² + 1) ≈ 0.333.
- f(-1) = -1 / (1² + 1) ≈ -0.333.
- f(4) = 4 / (4² + 1) ≈ 0.8.
- Therefore, the maximum value is approximately 0.8 and the minimum value is -0.333.
Learn more about value from the following link:
https://brainly.com/question/11546044
#SPJ11
Rachana has a set of ten mugs the set up is made of 3 different mugs
Answers
If Rachana randomly selects two mugs from the set, the probability that she gets two different mugs is 0.1556 or 15.56%.
To solve this problem, we can use the concept of combinations. Since there are 10 mugs in the set, there are 10 choose 2 = 45 ways to select two mugs without considering order.
Out of these 45 ways, we need to count the number of ways Rachana can select two different mugs. Since there are 3 different types of mugs, Rachana can choose any one of the three types for the first mug. There are 10 mugs in the set, out of which 3 belong to the chosen type. Therefore, the probability of choosing a mug of the chosen type is 3/10.
For the second mug, Rachana can choose from the remaining 9 mugs. Since she needs to choose a different type of mug, she can choose any one of the 2 remaining types. There are 7 mugs left from the other 2 types. Therefore, the probability of choosing a mug of a different type is (7/9) * 2/3 = 14/27.
Therefore, the probability of selecting two different mugs is the product of the probabilities of selecting a mug of the chosen type and a mug of a different type. This is given by (3/10) * (14/27) = 7/45, which is approximately 0.1556 or 15.56%.
To learn more about probability click on,
https://brainly.com/question/25905476
#SPJ4
Complete question is:
Rachana has a set of ten mugs the set up is made of 3 different mugs. If Rachana randomly selects two mugs from the set, what is the probability that she gets two different mugs?
792m rounded to 2 significant figures
Answers
Answer:
790 with a dash over the 9
Step-by-step explanation:
Martina is putting money into a savings account. She starts with s350 in the
savings account, and each week she adds $30.
Let s represent the total amount of money in the savings account (in
dollars), and let w represent the number of weeks Martina has been adding
money. Write an equation relating s to w. Then use this equation to find the
total amount of money in the savings account after 17 weeks.
Answers
===================================================
Explanation:
w = number of weekss = amount of money in savingsShe starts off with $350 in savings. Then she adds on another $30 per week. After w of those weeks, she adds a total of 30w dollars. The w is just a placeholder for a number. For example, if w = 5, then 30*w = 30*5 = 150 dollars is added on top of the $350 already there.
Overall, the expression 30w+350 represents how much is in her savings after w weeks. Therefore, the equation Martina wants would be
s = 30w+350
----------------------
For the second part, we'll plug w = 17 into that equation to find s
s = 30w+350
s = 30*17+350
s = 510+350
s = 860
Martina has $860 in her account after 17 weeks.