what are your answers to parts (a) through (c) if the standard deviation is thousand miles? if the standard deviation is thousand miles, the proportion of trucks that can be expected to travel between and thousand miles in a year is enter your response here
Answers
a. Proportion: 0.3944 b. Percentage: 5.81% c. At least 90%: 65 thousand miles d. Proportion (SD=9k): 0.4525 Percentage (SD=9k): 3.36% At least 90% (SD=9k): 62 thousand miles
a. First, let's calculate the z-scores:
For 35 thousand miles:
z = (x - μ) / σ = (35 - 50) / 12 = -1.25
For 50 thousand miles:
z = (x - μ) / σ = (50 - 50) / 12 = 0
Next, we can use a standard normal distribution table or a calculator to find the area under the curve between these z-scores. The area represents the proportion of trucks that can be expected to fall within this range.
Using a standard normal distribution table or a calculator, we find that the area to the left of z = -1.25 is 0.1056, and the area to the left of z = 0 is 0.5000.
Therefore, the proportion of trucks that can be expected to travel between 35 and 50 thousand miles in a year is:
Proportion = 0.5000 - 0.1056 = 0.3944 (rounded to four decimal places)
b.For less than 30 thousand miles:
z = (x - μ) / σ = (30 - 50) / 12 = -1.67
For more than 65 thousand miles:
z = (x - μ) / σ = (65 - 50) / 12 = 1.25
Again, using a standard normal distribution table or a calculator, we find that the area to the left of z = -1.67 is 0.0475, and the area to the left of z = 1.25 is 0.8944.
To find the percentage of trucks falling into either of these events, we can subtract the sum of these two areas from 1 and multiply by 100:
Percentage = (1 - (0.0475 + 0.8944)) * 100 = 5.81%
Therefore, the percentage of trucks that can be expected to travel either less than 30 or more than 65 thousand miles in a year is 5.81%.
c. To find the number of miles that will be traveled by at least 90% of the trucks, we need to find the z-score corresponding to the 90th percentile and then convert it back to the original mileage using the formula:
z = (x - μ) / σ
For a standard normal distribution, the z-score is approximately 1.28.
Plugging this value into the formula, we can solve for x:
1.28 = (x - 50) / 12
Rearranging the equation, we have:
12 * 1.28 = x - 50
x = 15.36 + 50 = 65.36
Therefore, at least 90% of the trucks will travel at most 65.36 thousand miles in a year. Rounded to the nearest mile, this becomes 65 thousand miles.
d. Let's re-calculate the answers to parts (a) through (c) using a standard deviation of
9 thousand miles.
For part (a):
z1 = (35 - 50) / 9 = -1.67
z2 = (50 - 50) / 9 = 0
Using the standard normal distribution table or a calculator, the area t the left of z = -1.67 is 0.0475, and the area to the left of z = 0 is 0.5000.
Proportion = 0.5000 - 0.0475 = 0.4525 (rounded to four decimal places)
For part (b):
z3 = (30 - 50) / 9 = -2.22
z4 = (65 - 50) / 9 = 1.67
Using the standard normal distribution table or a calculator, the area to the left of z = -2.22 is 0.0139, and the area to the left of z = 1.67 is 0.9525.
Percentage = (1 - (0.0139 + 0.9525)) * 100 = 3.36% (rounded to two decimal places)
For part (c):
z5 = 1.28
Solving for x:
1.28 = (x - 50) / 9
x = 11.52 + 50 = 61.52
Therefore, at least 90% of the trucks will travel at most 61.52 thousand miles in a year. Rounded to the nearest mile, this becomes 62 thousand miles.
Learn more about percentage here: https://brainly.com/question/12948737
#SPJ11
The complete question is:
A trucking company determined that the distance traveled per truck per year is normally distributed with a mean of 50 thousand miles and a standard deviation of 12 thousand miles. Complete parts (a) through (d) below. a. What proportion of trucks can be expected to travel between 35 and 50 thousand miles in a year? The proportion of trucks that can be expected to travel between 35 and 50 thousand miles in a year is b. What percentage of trucks can be expected to travel either less than 30 or more than 65 thousand miles in a year? The percentage of trucks that can be expected to travel either less than 30 or more than 65 thousand miles in a year is % c. How many miles will be traveled by at least 90% of the trucks? The number of miles that will be traveled by at least 90% of the trucks is miles, d. What are your answers to parts (a) through (c) if the standard deviation is 9 thousand miles? If the standard deviation is 9 thousand miles, the proportion of trucks that can be expected to travel between 35 and 50 thousand miles in a year is If the standard deviation is 9 thousand miles, the percentage of trucks that can be expected to travel either less than 30 or more than 65 thousand miles in a year is If the standard deviation is 9 thousand miles, the number of miles that will be traveled by at least 90% of the trucks is miles
Related Questions
Solve the inequality.
x+7≥18
Answers
Answer:
x is greater than or equal to 11.
Step-by-step explanation:
x+7≥18
7-7= 0 18-7=11
Bring down the x and the inequality to get...
x≥11
The solution to the inequality x + 7 ≥ 18 solved by isolating the value of x in the expression is x ≥ 11
Given the inequality :
x + 7 ≥ 18Subtract 7 from both sides
x + 7 - 7 ≥ 18 - 7
x ≥ 11
Therefore, te solution to the inequality is x ≥ 11
Learn more : https://brainly.com/question/14429071
O points
Find the measure of each angle indicated *
840

Answers
Answer:
168
Step-by-step explanation:
you take 84 and multipy it by to to get the answer.
345.5 - 131.75 (explain how to get that answer)
Answers
Answer: 213.75
Step-by-step explanation:
Add a zero to the hundredths place of 345.5 making it 345.50, then subtract as you would normally.
7. Suppose that in the backup web-server problem that we discussed in class, the main server is more reliable than the backup server-the probability that the main server fails is 1% while the probability that the backup server fails is 5%. As in class, assume that the two servers fail independently.
With this modification, find the chance that:
a) Both servers fail.
b) Exactly one of the servers fails.
c) At least one of the servers fails.
d) Do you think the assumption that the two servers fail independently is realistic?
What would make it more realistic? What would make it less realistic?
Answers
a) The chance that both servers fail is 0.05% (or 0.0005). b) The chance that exactly one of the servers fails is 5.9%. c) The chance that at least one of the servers fails is 5.95%. d) The assumption that the two servers fail independently may not be entirely realistic in all scenarios.
To find the probabilities in this scenario, we can use the probabilities of the main server and backup server failing, assuming they fail independently.
Let's denote:
P(M) = Probability of the main server failing = 0.01 (1%)
P(B) = Probability of the backup server failing = 0.05 (5%)
a) To find the chance that both servers fail, we need to calculate the probability of the intersection (AND) of the events:
P(both servers fail) = P(M) * P(B) = 0.01 * 0.05 = 0.0005 (0.05%)
b) To find the chance that exactly one of the servers fails, we can calculate the probability of the union (OR) of the mutually exclusive events:
P(exactly one server fails) = P(M) * (1 - P(B)) + (1 - P(M)) * P(B)
= 0.01 * (1 - 0.05) + (1 - 0.01) * 0.05
= 0.01 * 0.95 + 0.99 * 0.05
= 0.0095 + 0.0495
= 0.059 (5.9%)
c) To find the chance that at least one of the servers fails, we can calculate the probability of the complement (NOT) of both servers being operational:
P(at least one server fails) = 1 - P(both servers work)
= 1 - (1 - P(M)) * (1 - P(B))
= 1 - (1 - 0.01) * (1 - 0.05)
= 1 - 0.99 * 0.95
= 1 - 0.9405
= 0.0595 (5.95%)
d) The assumption that the two servers fail independently might not be entirely realistic in all scenarios. Factors such as shared infrastructure, common vulnerabilities, or external factors can introduce dependencies between the failure probabilities of the servers. If there are dependencies or shared factors that could cause correlated failures, the assumption of independence becomes less realistic.
To know more about chance,
https://brainly.com/question/26650929
#SPJ11
in anova testing, if the ratio of the between-treatment variability to within-treatment variability is significantly greater than one, then we
Answers
In ANOVA (Analysis of Variance) testing, if the ratio of the between-treatment variability to within-treatment variability, known as the F-statistic, is significantly greater than one, then we can conclude that there is a significant difference between the means of the treatment groups.
ANOVA is a statistical test used to compare the means of three or more groups to determine if there are significant differences among them. It partitions the total variability in the data into two components: the variability between the treatment groups and the variability within the treatment groups. The F-statistic is calculated by dividing the between-group variability by the within-group variability.
If the F-statistic is significantly greater than one, it indicates that the between-group variability is larger compared to the within-group variability. This suggests that the means of the treatment groups are different, and there is evidence of a significant effect of the treatment on the dependent variable.
To learn more about F-statistic click here : brainly.com/question/31577270
#SPJ11
i will give brianlist

Answers
Answer:
Hello! :) have a good day!
(10x+6)4 = 40x +24
HELP ME PLZZ I NEED HELP WITH THIS !!
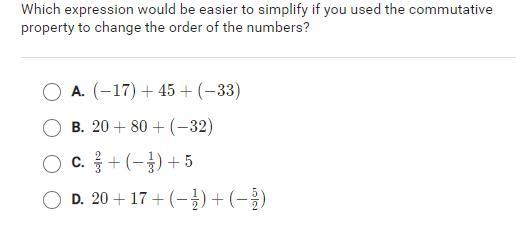
Answers
Answer:
i think its letter B.
I hope I help you
Answer:
I think it is A but i might be wrong.
Step-by-step explanation:
I feel this is a matter of opinion.
PLEASE HELP MEEEEEEEEEEEEEEEEEEEEEEEEEEE!!!!!!!!!!!! WILL GIVE BRAINLIEST IF RIGHT! 2 PPPL HAVE TO ANSWER FIRST

Answers
Answer: J
Step-by-step explanation:
\(log_2 24 - log_2 3 = log_2 (24/3) = log_2 8 = 3\)
So \(log_5 x = 3 -> x=125\)
help me with this question please

Answers
Answer:
N+1
Step-by-step explanation:
It begins with = 2
then n+1=3
then n+2=4 and so on it is n+1
State the equation of a line parallel to x = 3 going through the point (-10,3).
Answers
Answer:x=-10
Step-by-step explanation: We need to find the slope of the line to find equation.
slope of line x=3 is infinity.
equation of line parallel to x=3 will have same slope.
point given=(-10,3)
equation of line: (y-y1)=slope(x-x1)
= (y-3)=∞(x+10)
= (y-3)/∞=x+10
=0=x+10
=x=-10
How much sales tax will be changed at Store B
Answers
Answer:
8
Step-by-step explanation:8
A group of students is timed while sprinting 100 meters. Each student’s speed can be found by dividing 100 m by their time. Is each statement true or false?
Speed is a function of time.
Time is a function of distance.
Speed is a function of number of students racing.
Time is a function of speed.
Answers
B.Time is a function of distance. is the answer ot the question
A group of students is timed while sprinting 100 meters. Each student’s speed can be found by dividing 100 m by their time. Is each statement true or false?
Speed is a function of time.
Time is a function of distance.
Speed is a function of number of students racing.
Time is a function of speed.
Multiply: a^−4(a^2)(a^−5)

Answers
Answer:
a^(-7)
Step-by-step explanation:
To multiply these terms, we can add the exponents of the same base, then simplify if possible.
a^−4(a^2)(a^−5) = a^( -4+2-5 ) = a^(-7)
Therefore,
a^−4(a^2)(a^−5) = a^(-7)
a^−4(a^2)(a^−5) = a^(-4+2-5) = a^(-7)
Therefore, the simplified expression is a^(-7).
Option B
Solve the problem. A small private college is interested in determining the percentage of its students who live off campus and drive to class. Specifically, it was desired to determine if less than 20% of their current students live off campus and drive to class. The college decided to take a random sample of 108 of their current students to use in the analysis. In the sample size of n - 108 large enough to use this inferential procedure? O Yes, since 230 O Yes, since the central limit there works whenever proportions are used O Yes since both and are greater than or equal to 15
O No A random sample of n = 300 measurements is drawn from a population with probability of success 26. Find the 95% confidence interval for p
a) 0.26 (1-0.26) 0.26 +1.96 300 b) 0.26 +2.63 0.26 (1 -0.26) 300 c) 0.26 + 300 0.26 (1-0.26) 1.96
d) 0.26.95 0.26. (1-0.26) 300
Answers
The 95% confidence interval for p is 0.26 ± 2.63 * sqrt((0.26 * (1 - 0.26)) / 300). The correct answer is option b.
For the first problem:
The question asks whether a sample size of n = 108 is large enough to use an inferential procedure. The correct answer is: O Yes, since both n and np (where p is the proportion of interest) are greater than or equal to 15.
To determine if a sample size is large enough to use an inferential procedure for proportions, both the sample size (n) and the product of the sample size and the proportion of interest (np) should be greater than or equal to 15. In this case, n = 108, and since the proportion is not provided, we cannot verify whether np is greater than or equal to 15. Therefore, we cannot determine if the sample size is large enough based on the information given.
For the second problem:
To find the 95% confidence interval for p (proportion), we can use the formula:
p ± z * sqrt((p * (1 - p)) / n)
p = 0.26 (probability of success)
n = 300 (sample size)
z = 1.96 (z-value for a 95% confidence level)
Using the formula, the 95% confidence interval for p is:
0.26 ± 1.96 * sqrt((0.26 * (1 - 0.26)) / 300)
Therefore, the correct answer is option b.
To know more about confidence interval refer to-
https://brainly.com/question/32278466
#SPJ11
4. Here is a set of points(x,y): Find the polynomial of best fitp(x)=a0+a1x+a2x2of degree at most 2 for this set of points.
Answers
The polynomial of best fit for this set of points is p(x) = a0 + a1x + a2x^2, where a0, a1, and a2 are the coefficients that minimize the sum of the squared differences between the actual y-values and the predicted y-values of the polynomial.
The polynomial of best fit for a set of points is the polynomial that most closely fits the points. In order to find the polynomial of best fit, we need to use the method of least squares. This involves finding the coefficients a0, a1, and a2 that minimize the sum of the squared differences between the actual y-values and the predicted y-values of the polynomial.
1. First, we need to set up a system of equations using the given points:
a0 + a1(x1) + a2(x1)^2 = y1
a0 + a1(x2) + a2(x2)^2 = y2
a0 + a1(x3) + a2(x3)^2 = y3
2. Next, we need to solve this system of equations for a0, a1, and a2. This can be done using matrix operations or by using substitution and elimination.
3. Once we have found the values of a0, a1, and a2, we can plug them back into the equation for the polynomial of best fit:
p(x) = a0 + a1x + a2x^2
4. Finally, we can use this polynomial to make predictions for other x-values and compare them to the actual y-values to see how well the polynomial fits the data.
So, the polynomial of best fit for this set of points is p(x) = a0 + a1x + a2x^2, where a0, a1, and a2 are the coefficients that minimize the sum of the squared differences between the actual y-values and the predicted y-values of the polynomial.
Learn more about points
brainly.com/question/30891638
#SPJ11
6.
Which of the following equations describes the graph?
A. y= -2x^2 - 4
B. y= 2x^2 + 4
C. y= -2x^2 + 4
D. y= 2x^2 - 4

Answers
Answer:
C. y= -2x^2 + 4
Step-by-step explanation:
Graph the parabola using the direction, vertex, focus, and axis of symmetry.
Direction: Opens Down
Vertex:
(
0
,
−
4
)
Focus:
(
0
,
−
33
8
)
Axis of Symmetry:
x
=
0
Directrix:
y
=
−
31
8
x
y
−
2
−
12
−
1
−
6
0
−
4
1
−
6
2
−
12
________________
Graph the parabola using the direction, vertex, focus, and axis of symmetry.
Direction: Opens Up
Vertex:
(
0
,
4
)
Focus:
(
0
,
33
8
)
Axis of Symmetry:
x
=
0
Directrix:
y
=
31
8
x
y
−
2
12
−
1
6
0
4
1
6
2
12
______________
Graph the parabola using the direction, vertex, focus, and axis of symmetry.
Direction: Opens Down
Vertex:
(
0
,
4
)
Focus:
(
0
,
31
8
)
Axis of Symmetry:
x
=
0
Directrix:
y
=
33
8
x
y
−
2
−
4
−
1
2
0
4
1
2
2
−
4
_______________
Graph the parabola using the direction, vertex, focus, and axis of symmetry.
Direction: Opens Up
Vertex:
(
0
,
−
4
)
Focus:
(
0
,
−
31
8
)
Axis of Symmetry:
x
=
0
Directrix:
y
=
−
33
8
x
y
−
2
4
−
1
−
2
0
−
4
1
−
2
2
4




A rectangle is shown. The length of the rectangle is labeled 6 inches. The width of the rectangle is labeled 9 inches.
What are the dimensions of the poster at one-third its current size?
1. 2 in by 3 in
2. 3 in by 3 in
3. 18 in by 27 in
4. 12 in by 18 in
Answers
Answer:
1, 2 in by 3 in.
Step-by-step explanation:
It's asking the dimensions of the poster after it's one-third of the size. So you divide the dimensions by 3. So 6/3=2 and 9/3=3. Hopefully this is right and helps you out.
juliet rented a car for one day from a company that charges $80 per day plus $0.15 per mile driven. if she was charged a total of $98 for the rental and mileage, for how many miles of driving w
Answers
Juliet was charged $18 for driving 120 miles.
Given,
The rent of car per day = $80
The charge for per miles driven = $0.15
Juliet was charged a total of $98 for the rental and mileage.
We have to find the total miles of driving;
Here,
Charge for miles driven = Total charge - Rent of car for a day
Charge for miles driven = 98 - 80
Charge for miles driven = $18
Now,
Total miles driven = Charge for miles driven / Charge for one mile
Total miles driven = 18/0.15
Total miles driven = 120
That is,
Juliet was charged $18 for 120 miles of driving.
Learn more about charge for driving here;
https://brainly.com/question/13250700
#SPJ4
A volleyball camp chargers $150 per camper for 10 campers. When a team brings 15 campers, the rate is reduced to $125 per camper. What is the rate of change in cost per camper ?
Answers
Answer: $6.67
Step-by-step explanation:
A volleyball camp chargers $150 per camper for 10 campers. The cost for each camper will be:
= $150/10
= $15
When a team brings 15 campers, the rate is reduced to $125 per camper. The cost for each camper will be:
= $125/15
= $8.33
The rate of change in cost per camper will be:
= $15 - $8.33
= $6.67
mr. way must sell stocks from 3 of the 6 companies whose stocks he owns so that he can send his children to college. if he chooses the companies at random, what is the probability that the 3 companies will be the 3 with the best future earnings? (enter your probability as a fraction.)
Answers
The probability that the 3 companies will be the 3 with the best future earnings is 5/100 .
There are a total of 20 possible combinations of 3 companies that Mr. Way can sell stocks from. However, we are only interested in the probability of him selecting the 3 companies with the best future earnings. Since we do not know the actual future earnings of each company, we can assume that all 6 companies have an equal chance of being in the top 3.
Therefore, the probability of Mr. Way selecting the 3 companies with the best future earnings is the same as the probability of selecting any specific set of 3 companies out of the 6.
The number of ways to select 3 companies out of 6 is given by the combination formula, which is:
6! / (3! x 3!) = 20
Therefore, the probability of Mr. Way selecting the 3 companies with the best future earnings is 1/20. So, the answer is:
Probability = 1/20
This can also be written as a fraction, which is probability = 0.05 or 5/100
Learn more about probability here,
https://brainly.com/question/27990267
#SPJ11
Read the following sentences from the passage: "When LeBron James jumps, he pushes down on the surface of the court. This is the 'action' that Newton mentions in his Third Law."
Based on this information, LeBron James jumping is an example of which part of Newton's Third Law?
A. both the action and the equal and opposite reaction
B. the equal and opposite reaction of an action
C. the action which causes an equal and opposite reaction
D. neither the action nor the equal and opposite reaction
Answers
The action that results in an equivalent and opposite reaction is C, making it the right response.
Based on the information provided in the passage, LeBron James jumping is an example of the action that Newton mentions in his Third Law. The Third Law states that for every action, there is an equal and opposite reaction. When LeBron James jumps, he exerts a force (action) on the surface of the court, pushing it down. According to Newton's Third Law, the surface of the court will exert an equal and opposite force (reaction) on LeBron James, pushing him upwards.
Therefore, the correct answer is C: the action which causes an equal and opposite reaction.
To learn more about Newton's Third Law refer to:
brainly.com/question/29768600
#SPJ4
2x - y = -1
4x - 2y = 6
Graphing
Answers
Answer: No Solution.
Step-by-step explanation:
To solve the system of equations 2x - y = -1 and 4x - 2y = 6 graphically, we can plot the two lines represented by each equation on the same coordinate plane and find the point of intersection, if it exists.
To graph the line 2x - y = -1, we can rearrange it into slope-intercept form:
y = 2x + 1
This equation represents a line with slope 2 and y-intercept 1. We can plot this line by starting at the y-intercept (0, 1) and moving up 2 units and right 1 unit to find another point on the line. Connecting these two points gives us the graph of the line (Look at the first screenshot).
To graph the line 4x - 2y = 6, we can rearrange it into slope-intercept form:
y = 2x - 3
This equation represents a line with slope 2 and y-intercept -3. We can plot this line by starting at the y-intercept (0, -3) and moving up 2 units and right 1 unit to find another point on the line. Connecting these two points gives us the graph of the line (Look at the second screenshot).
We can see from the graphs that the two lines are parallel and do not intersect. Therefore, there is no point of intersection and no solution to the system of equations.


Whitney,Andrew,and Lena all have summer jobs.Whitney earns 312 in 26 hours of work.Andrew earns 451 in 41 hours of work.Lena earns 10 per hour.Who earns the most money per hour
Answers
According to the given data we have the following:
Whitney earns 312 in 26 hours of work
Andrew earns 451 in 41 hours of work
Lena earns 10 per hour
In order to calculate who earns the most money per hour we would have to calculate the rate of money per hour of Whitney and Andrew and the compare it with Lena.
So, money per hour of whtiney=312/26
money per hour of whtiney=12 per hour
money per hour of Andrew=451/41
money per hour of Andrew=11 per hour
Therefore, Whitney is the person that earns most money per hour.
5000 people visit a website. 95% stay more than 2 minutes how many people visiting the website stay for more than 2 minutes
Answers
Answer:
4750
Step-by-step explanation:
Take 95, move the decimal. 0.95
then multiply 5000 by 0.95
What is the value of x for number 4

Answers
Answer:
4
Step-by-step explanation:
A participant took 5. 2 hours to complete a marathon. How many minutes did the participant take to complete the marathon? use 1 hour = 60 minutes.
Answers
312 minutes the participant took to complete the marathon
Unit conversion is a process with multiple steps that involves multiplication or division by a numerical factor or, particularly a conversion factor. The process may also require selection of the correct number of significant digits, and rounding.
According to the question,
The time taken by participant to complete a marathon in hours = 5.2 hours
1 hour contains 60 minutes
so, to change hours into minutes , we have to multiple hours into 60
Time taken by participant to complete a marathon in minutes = 5.2 × 60
=> 312 minutes
To know more about Unit conversion here
https://brainly.com/question/12709593
#SPJ4
Define the nonprobability sampling methods and give examples of each.
Answers
Sampling is the use of a subset of the population to represent the whole population or to inform about processes that are meaningful beyond the particular cases, individuals or sites studied.
In non-probability sampling, the sample is selected based on non-random criteria, and not every member of the population has a chance of being included. Common non-probability sampling methods include convenience sampling, voluntary response sampling, purposive sampling, snowball sampling, and quota sampling.
Can someone help solve the problems 2-4

Answers
Answer:
1234567891011121314151617181920
Step-by-step explanation:
you just count
Is the sequence an= 4 + 2n arithmetic?

Answers
Answer:
Sorry am not answer that because am desperate for points so am just going to get some points
11. Give two examples of each type of number: real, natural, integers, rational and irrational.
Answers
Answer:
real:√2, 3,-1, 1/2 etc
natural: 1,2,3,4,5,6.....(0 is not included)
integers:. .............-4,-3,-2,-1,0,1,2,3,4........ etc
rational: nos. which are in p/q form
:1/2,3/4,4/9 etc
irrational: nos. which cannot be written in p/q form
: √2,√3... etc
irrational: √2, √3, √5, √11, √21, π(Pi)