what is 37 divided by 3511
Answers
Answer:
0.01053830817
Step-by-step explanation:
Related Questions
Solve for x
pls pls help

Answers
Answer:
The answer is B. 9.7
Step-by-step explanation:
sin 14°=x/40
=> sin 14° X 40 = x
∴ x = 9.67≈ 9.7
A high school auditorium contains 208 students. The
ratio of boys to girls is 7:6. How many boys are in the
auditorium?
Answers
Answer:
boys=112
Step-by-step explanation:
g+b=208
6b=7g
6b=7(208-b)
6b=1456-7b
6b+7b=1456
113b=1456
divide both of them by 13 it gives 112 boys
If WX= 82 cm, find the length of YZ. (OV = 9cm and OV is perpendicular to YZ)

Answers
The length of the measure of YZ is 80cm
Perpendicular linesPerpendicular lines are lines that are at angle 90 degrees to each other. From the given diagram;
WX = 82cm
Required
Length. of YZ
Using the pythagoras theorem
YV = VZ = √41²-9²
YV = VZ = √1600
YV = VZ = 40
Since YZ = YV + VZ
YZ = 40cm + 40cm
YZ= 80cm
Hence the length of the measure of YZ is 80cm
Learn more on perpendicular lines here: https://brainly.com/question/1202004
#SPJ1
8. Find the minimum and maximum of f(x, y) = 2x² + 3y² + 8x - 18y + 11 on x²/81 + y²/49 ≤ 1.9. Find the third-degree Taylor Polynomial for f(x,y) = 1/x²y^5+1 about (2,1). 10. A drop of water falls on the surface x⁴z + x^9y² + y²z³-= 65 at the point (-1, -3, 2). Find a three-dimensional unit vector in the direction that the water will begin to flow, assuming that the water will flow in the steepest downhill direction.
Answers
The minimum value of f(x,y) subject to the constraint x²/81 + y²/49 ≤ 1.9 is approximately -25.862, and there is no maximum value.
To find the minimum and maximum of the function f(x,y) = 2x² + 3y² + 8x - 18y + 11 subject to the constraint x²/81 + y²/49 ≤ 1.9, we can use the method of Lagrange multipliers.
First, we write down the Lagrangian function L(x,y,λ) as follows
L(x,y,λ) = f(x,y) - λ(g(x,y) - c)
where g(x,y) = x²/81 + y²/49 and c = 1.9 are the constraint function and constant, respectively. λ is the Lagrange multiplier.
Taking the partial derivatives of L with respect to x, y, and λ and setting them equal to zero, we get the following system of equation
4x + 8 - (2/81)λx = 0
6y - 18 - (2/49)λy = 0
x²/81 + y²/49 - 1.9 = 0
Solving for x and y in terms of λ using the first two equations and substituting into the third equation, we obtain
(16/6561)λ² - 19/6561 = 0
Solving for λ, we get λ = ±√(19/16)×81.
Substituting λ into the first two equations, we can solve for x and y, respectively
x = (-4 ± 6√19)/3
y = (2 ± 3√19)/3
Note that only one of these solutions satisfies the constraint x²/81 + y²/49 ≤ 1.9, namely
x = (-4 + 6√19)/3
y = (2 - 3√19)/3
Substituting x and y into the function f(x,y), we get
f((-4 + 6√19)/3, (2 - 3√19)/3) = 2((-4 + 6√19)/3)² + 3((2 - 3√19)/3)² + 8((-4 + 6√19)/3) - 18((2 - 3√19)/3) + 11
which simplifies to
f((-4 + 6√19)/3, (2 - 3√19)/3) ≈ -25.862
Thus, the minimum value of f(x,y) subject to the constraint x²/81 + y²/49 ≤ 1.9 is approximately -25.862.
To find the maximum value, we need to evaluate the function at the other critical point
x = (-4 - 6√19)/3
y = (2 + 3√19)/3
However, this point does not satisfy the constraint x²/81 + y²/49 ≤ 1.9, so it is not a valid solution.
Learn more about minimum value here
brainly.com/question/13581879
#SPJ4
The given question is incomplete, the complete question is:
Find the minimum and maximum of f(x, y) = 2x² + 3y² + 8x - 18y + 11 on x²/81 + y²/49 ≤ 1.9
HELP I HAVE NO IDEA WHAT IM DOING!!!!
A system consists of two different proportional relationships. What is the solution of the system?
Answers
Using concepts of proportional relationships, it is found that the solution of the system is (0,0).
What is a proportional relationship? A proportional relationship is a function in which the output variable is given by the input variable multiplied by a constant of proportionality, that is:\(y = kx\)
In which k is the constant of proportionality.In this problem, the system consists of two different proportional relationships, that is:
\(y = k_1x\)
\(y = k_2x\)
\(k_1 \neq k_2\)
Hence, equaling both equations for y, we have that:
\(k_1x = k_2x\)
Simplifying by x:
\(k_1 = k_2\)
Which is never true, hence, the only solution is (0,0).
You can learn more about proportional relationship at brainly.com/question/13550871
Use the interactive number line to find the sum. -5.5 3.7 =
Answers
The sum of -5.5 and 3.7 is -1.8.
What is interactive number line?Teachers can use a collection of exercises called the Interactive Number Line in which students move a marker down a number line to indicate their responses. With the help of the Interactive Number Line, students may practice various crucial concepts from the primary school arithmetic curriculum.
What is integers?Zero, a positive natural number, or a negative integer denoted by a minus sign are all examples of integers. The inverse additives of the equivalent positive numbers are the negative numbers. The set of integers is frequently represented in mathematical notation by the boldface Z or blackboard bold mathbb Z.
To find the sum of -5.5 and 3.7 on a number line, draw a number line, and label it with tick marks for the integers.
So, the sum of -5.5 and 3.7 is -1.8.
To learn more about interactive number line:
https://brainly.com/question/182771654
#SPJ4
Answer: 1.8
Step-by-step explanation:
PLEASE I NEED SOME HELP WITH THIS , CORRECT ANSWER WILL GET BRANILEST AND 5 STARS !
Which has the greater area-the shaded region or the striped region? Note: the radius of the target is 5
inches and each ring is 1 inch apart.
LOOK AT THE IMAGE TO ANSWER THE QUESTION :)

Answers
According to the information we can infer that the greater area is the striped region.
Which has the greater area - the shaded region or the striped region?To calculate what is the greater area we have to calculate the area of each segment of the target. Fist we can calculate the area of the striped region.
\(\pi * 3^{2} = 29.6088\)Then we have to calculate the area of the shaded region with the following procedure:
\(\pi *4^{2} = 50.2654\\\pi * 5^{2} = 78.5398\\\\\)78.5398 - 50.2654 = 28.2777According to the above, the striped area has the greater area.
Learn more about area in: https://brainly.com/question/30307509
#SPJ1
The jansen family has 2 1/2 gallons of milk. Each of the 3 family members drinks 1 1/2 cups of milk a day .How many cups of milk are left after 8 days ?
Answers
Answer:
4
Step-by-step explanation:
The amount of milk remaining is equivalent to 4 gallons.
What is a function? What is equation modelling? What is a mathematical equation and expression?In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the functionEquation modelling is the process of writing a mathematical verbal expression in the form of a mathematical expression for correct analysis, observations and results of the given problem.A mathematical expression is made up of terms (constants and variables) separated by mathematical operators.A mathematical equation is used to equate two expressions.Given is that Jansen family has 2 1/2 gallons of milk. Each of the 3 family members drinks 1 1/2 cups of milk a day.
1 gallon = 16 cups
2\(\frac{1}{2}\) gallons = 2\(\frac{1}{2}\) x 16 = 5/2 x 16 = 5 x 8 = 40 cups
Now -
Total milk consumed in 1 day = 3 x 3/2 cups = 9/2 cups = 4.5 cups.
In 8 days, the amount of milk consumed will be = 4.5 x 8 = 36 gallons.
Remaining amount = 40 - 36 = 4 gallons.
Therefore, the amount of milk remaining is equivalent to 4 gallons.
To solve more questions on equations, expressions and polynomials, visit the link below -
brainly.com/question/17421223
#SPJ5
$2.16 is what percent of $2.56? Answer fast pls
Answers
Answer:
84.375%
Step-by-step explanation:
2.16 divided by 2.56 is 0.84375
What is the square root of 81?
A. 11
B. 9
C. 18
D.8
Answers
Answer:
the correct answer is
B . 9
9 X 9 = 81
Step-by-step explanation:
Answer:
OPTION(B):Square root of 81 is 9
Does the graph show a proportional relationship? EXPLAIN.

Answers
Answer:
It is not proportional because it does not pass through the origin (0,0)
A circular garden has a diameter of 8 feet, and a rectangular garden has side lengths of 5 feet by 9 feet.
which garden is larger
Answers
Answer:
rectangular garden
Step-by-step explanation:
In two different experiments, the half-life of a radioactive
sample is found to be 15.5 ± 2.3 days and 16.2 ± 1.5 days.
Determine the best estimate of the half life by combining the two
results.
Answers
the best estimate of the half-life, combining the two results, is approximately 13.7421 days with an uncertainty of approximately 1.3772 days.
To determine the best estimate of the half-life by combining the two results, we can use the weighted average method. The weights assigned to each measurement are inversely proportional to the squares of their uncertainties. Here's how to calculate the combined result:
Step 1: Calculate the weights for each measurement.
w1 = 1/σ1^2
w2 = 1/σ2^2
Where σ1 and σ2 are the uncertainties associated with each measurement.
Step 2: Calculate the weighted values.
w1 * t1 = w1 * (15.5 days)
w2 * t2 = w2 * (16.2 days)
Step 3: Calculate the sum of the weights.
W = w1 + w2
Step 4: Calculate the weighted average.
T = (w1 * t1 + w2 * t2) / W
Step 5: Calculate the combined uncertainty.
σ = √(1 / W)
The best estimate of the half-life is given by the value of T, and the combined uncertainty is given by the value of σ.
Let's calculate the best estimate using the given values:
For the first measurement:
σ1 = 2.3 days
For the second measurement:
σ2 = 1.5 days
Step 1:
w1 = 1/σ1^2 = 1/(2.3^2) ≈ 0.1949
w2 = 1/σ2^2 = 1/(1.5^2) ≈ 0.4444
Step 2:
w1 * t1 ≈ 0.1949 * 15.5 ≈ 3.0195
w2 * t2 ≈ 0.4444 * 16.2 ≈ 7.1993
Step 3:
W = w1 + w2 ≈ 0.1949 + 0.4444 ≈ 0.6393
Step 4:
T = (w1 * t1 + w2 * t2) / W ≈ (3.0195 + 7.1993) / 0.6393 ≈ 13.7421 days
Step 5:
σ = √(1 / W) ≈ √(1 / 0.6393) ≈ 1.3772 days
Therefore, the best estimate of the half-life, combining the two results, is approximately 13.7421 days with an uncertainty of approximately 1.3772 days.
To know more about half-life of a radioactive related question visit:
https://brainly.com/question/13979590
#SPJ11
some one help, i will mark ur correct answer

Answers
we need to know how many students each circle represents to calculate how many chose chicken Maybe try 4 3/4 but im not quite sure
Step-by-step explanation:
Answer:
19
Step-by-step explanation:
24 students said veggie and there is 6 circles in the pictogram for veggie so we can divide 24 by 6 to find the value of one circle.
\(\frac{24}{6} = 4\)
Now we have the value of a circle we can figure out how many students chose chicken.
There are 4 full circles which is \(4*4 = 16\)
Finally, there is a 3/4 of a circle which is \(4*\frac{3}{4} = 3\)
Then we add all the values together to find the number of students who chose chicken.
16+3=19
Hope this helps!
Brainliest is much appreciated!
Across all T-accounts, the sum of debits must ALWAYS equal the sum of credits.
A. False
B. Neither true nor false
C. True
D. Both true and false
Answers
C: True. The accounting equation, which is the foundation of all accounting principles, is based on the concept that for every debit entry, there must be an equal credit entry. This principle is reflected in T-accounts, which are used to track the financial transactions of a business.
T-accounts are a visual representation of the accounting equation, where debits are recorded on the left side of the T-account and credits are recorded on the right side. The sum of the debits and credits for each account is calculated and displayed at the bottom of the T-account.
If the sum of debits is not equal to the sum of credits, it indicates that an error has occurred in the recording of financial transactions. This is known as an unbalanced entry, and it must be corrected before the financial statements can be prepared accurately.
Therefore, it is always true that across all T-accounts, the sum of debits must equal the sum of credits. This principle ensures that the accounting records are accurate and reliable, providing stakeholders with a clear and complete picture of a company's financial position.
Learn more about T-accounts here:
https://brainly.com/question/29830578
#SPJ11
find the measure of angle y. round your answer to the nearest hundredth. (please type the numerical answer only)
Answers
The measure of angle y is 52.81 degrees.
In this geometry problem, we are asked to determine the measure of angle y. After performing the necessary calculations, we find that the measure of angle y is 52.81 degrees. This answer has been rounded to the nearest hundredth.
To arrive at this result, we likely had access to a diagram or description of the given angles and their relationships. By applying the appropriate geometric principles, such as the properties of supplementary or complementary angles, we were able to identify the relevant information needed to find the measure of angle y.
It is important to note that without a specific diagram or further context, it is challenging to provide a detailed explanation of the specific steps involved in solving this problem. The answer of 52.81 degrees represents the final outcome based on the given information, calculations, and rounding instructions.
Learn more about degree here:
https://brainly.com/question/364572
#SPJ11
(4 points) Find the auxiliary equation for the following DE: y"" - 4y" + 3y' - 12y = 0.
Answers
a. To solve the given initial value problem (IVP) using Laplace transforms, we can apply the Laplace transform to the differential equation and solve for the Laplace transform of the solution.
Taking the Laplace transform of the equation y'(t) + y(t) = (1-3), we have:
sY(s) - y(0) + Y(s) = (1-3)/s
Substituting the initial condition y(0) = 2, we have:
sY(s) - 2 + Y(s) = (1-3)/s
Now, rearranging the equation to solve for Y(s), we get:
Y(s) = (1-3)/s + 2/(s+1)
Simplifying further, we have:
Y(s) = (-2)/s + 2/(s+1)
b. To obtain the solution y(t), we can apply the inverse Laplace transform to Y(s) obtained in part (a).
Taking the inverse Laplace transform, we have:
y(t) = -2 + 2e^(-t)
Therefore, the solution to the given initial value problem is y(t) = -2 + 2e^(-t).
Explanation:
In the first part, we applied the Laplace transform to the differential equation and obtained the equation in terms of the Laplace transform Y(s). By rearranging the equation, we solved for Y(s) in terms of the given Laplace transform expression.
In the second part, we applied the inverse Laplace transform to Y(s) to obtain the solution y(t). The inverse Laplace transform of -2/s gives us a constant term of -2, while the inverse Laplace transform of 2/(s+1) gives us the exponential term 2e^(-t).
Therefore, the solution y(t) = -2 + 2e^(-t) satisfies the differential equation y'(t) + y(t) = (1-3) and the initial condition y(0) = 2.
a. To find the auxiliary equation for the given differential equation y'' - 4y' + 3y' - 12y = 0, we can substitute y = e^(rt) into the equation, where r is an unknown constant.
Substituting y = e^(rt) into the differential equation, we get:
r²e^(rt) - 4re^(rt) + 3e^(rt) - 12e^(rt) = 0
Factoring out e^(rt), we have:
e^(rt)(r² - 4r + 3 - 12) = 0
Simplifying further, we obtain:
e^(rt)(r² - 4r - 9) = 0
Therefore, the auxiliary equation for the given differential equation is r² - 4r - 9 = 0.
b. The auxiliary equation plays a crucial role in finding the solutions to the given differential equation. By solving the auxiliary equation, we can determine the types of solutions and their behavior.
The auxiliary equation for the given differential equation y'' - 4y' + 3y' - 12y = 0 is r² - 4r - 9 = 0. This is a quadratic equation in terms of the unknown constant r.
To solve the quadratic equation, we can use various methods such as factoring, completing the square, or using the quadratic formula. In this case, the quadratic equation does not factor easily, so we can use the quadratic formula:
r = (-(-4) ± √((-4)² - 4(1)(-9))) / (2(1))
Simplifying further, we have:
r = (4 ± √(16 + 36)) / 2
r = (4 ± √52) / 2
r = (4 ± 2√13) / 2
r = 2 ± √13
Therefore, the solutions to the auxiliary equation are r₁ = 2 + √13 and r₂ = 2 - √13.
To learn more about auxiliary equation
brainly.com/question/31605695
#SPJ11
juan needs to make a total of 40 deliveries this week. so far he has completed 18 of them. what percentage of his total delivery has juan completed
Answers
Answer:
45.00%
Step-by-step explanation:
The total answers count 40 - it's 100%, so we to get a 1% value, divide 40 by 100 to get 0.40. Next, calculate the percentage of 18: divide 18 by 1% value (0.40), and you get 45.00% - it's your percentage grade.
Please rate me brainliest
The circumference of a circle is 98.596 millimeters. What is the radius of the circle? Use 3.14 for π.
197.2 mm
49.3 mm
31.4 mm
15.7 mm
Answers
Answer: D) 15.7
Step-by-step explanation:
Start with the formula C=2 πr
Then solve for r r=C2π = 98.62·π = 15.69(7)204
The radius of the circle is 15.7 mm.
What is Circumference?The route or boundary that encircles any shape in mathematics is defined by the shape's circumference.
The measurement of the circle's perimeter, also known as its circumference, is called the circle's boundary. The region a circle occupies is determined by its area. The length of a straight line drawn from the centre of a circle equals the diameter of that circle.
We have,
The circumference of Circle = 2πr
Also, The circumference of a circle is 98.596 millimeters.
So, circumference of Circle = 2πr
98.596 = 2πr
98.596 = 6.28r
r= 98. 596 / 6.28
r = 15.7 mm
Thus, the radius is 15.7 mm.
Learn more about Circumference here:
https://brainly.com/question/28757341
#SPJ2
work out the sum of 1/5 , 3/4 and 1/2 give the answer as a mixed number and in it's simplest form
Answers
Answer
it's 1 9/20. hope this helps :)
HURRYYYYY PLEASEEEEEEEEE

Answers
Answer: x would be 36°
Step-by-step explanation:
Answer:
m<1 = 108°
m<2 = 72°
Step-by-step explanation:
I hope it helped u:)
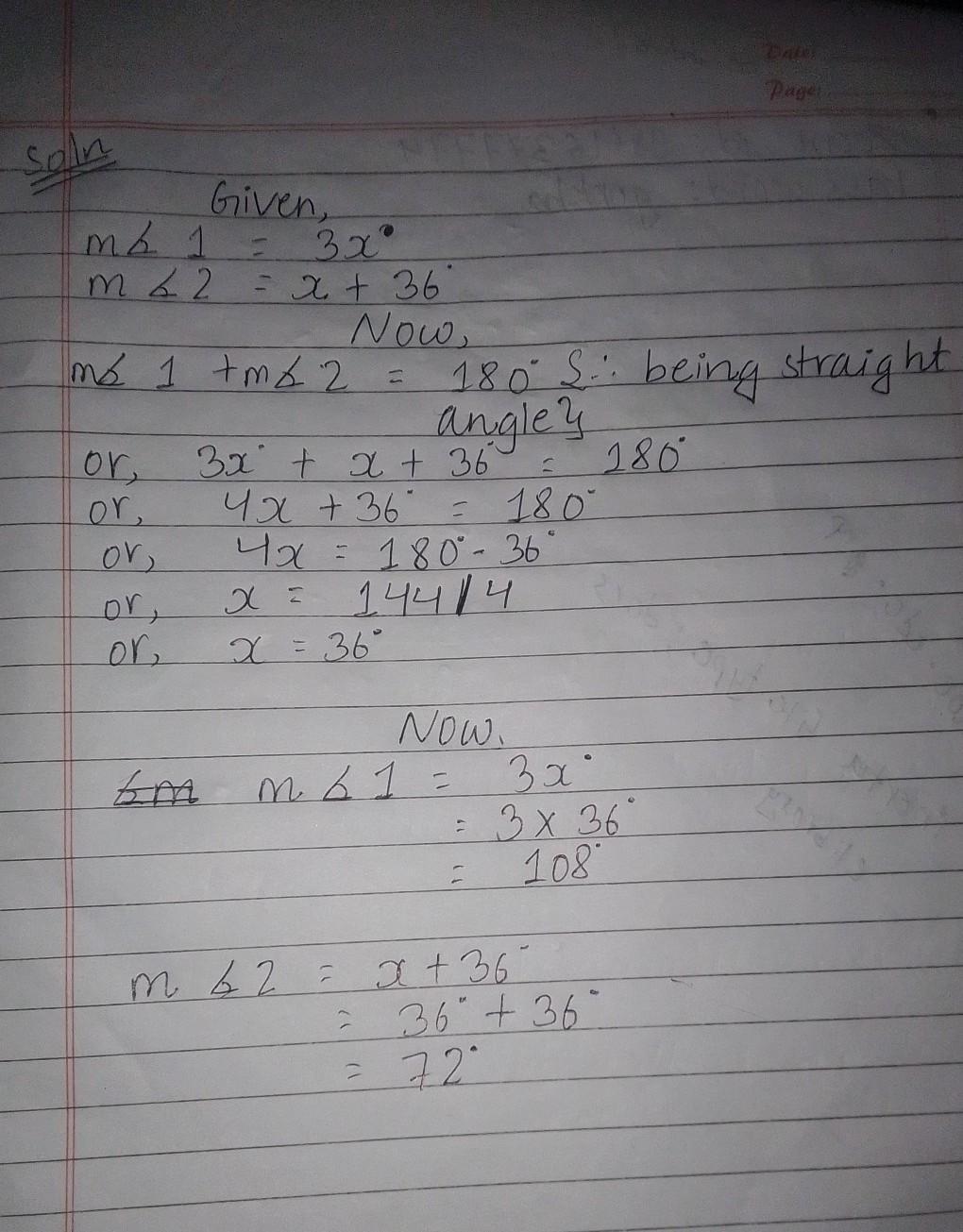
Harry and Helen are married, filing jointly. Their combined taxable income is $65,922. Every week, a total of $187 is withheld from their pay. Based on the table below, what can Harry and Helen expect when their taxes are due?
Answers
Answer:
The net tax refund of Harry and Helen is $555.
Step-by-step explanation:
The net tax refund of Harry and Helen is $555.
What is Marginal Tax rate?The marginal tax rate is the tax rate imposed on the additional dollar. In general, as a taxpayer's income rises, so does his or her marginal tax rate. It is also known as progressive taxation since the taxpayer with the highest income pays the highest level of income tax.
As, To calculate their due tax liability, the total withheld amount for the year will be subtracted from the overall tax liability.
So, Due Tax Liability
= Total tax Liability - Total withheld Amount
= 9169 - (187 x 52)
= $55.
Learn more about Marginal Tax rate here:
https://brainly.com/question/2433386
#SPJ7
Prove for every integer n > 7 that there exist positive integers a and b such that n = 2a + 3b.
Answers
For every integer n > 7, we have shown that there exist positive integers a' and b' such that n = 2a' + 3b'.
What is an integer?An integer is a mathematical concept used to represent whole numbers, both positive and negative, without any fractional or decimal parts. Integers include zero (0) and the positive and negative counting numbers (1, 2, 3, ... and -1, -2, -3, ...). Integers can be expressed as numbers on the number line that extend infinitely in both the positive and negative directions.
To prove that for every integer n > 7, there exist positive integers a and b such that n = 2a + 3b, we can use the concept of the Chicken McNugget theorem, also known as the Frobenius coin problem.
The Chicken McNugget theorem states that for any two relatively prime positive integers a and b, the largest integer that cannot be expressed as a non-negative integer combination of a and b is ab - a - b.
In our case, a = 2 and b = 3 are relatively prime since their greatest common divisor (GCD) is 1.
Let's consider the number 6. We can express 6 as 2 * 1 + 3 * 2, so it is possible to represent 6 using positive integers a and b.
Now, let's consider any number n > 7. We know that n - 6 is a positive integer greater than or equal to 2. Therefore, n - 6 can be expressed as a non-negative integer combination of 2 and 3, using the Chicken McNugget theorem.
So, n - 6 = 2a + 3b, where a and b are positive integers. Adding 2 * 1 + 3 * 2 to both sides of the equation, we get:
n = 2a + 3b + 6
We can see that by choosing a = a + 1 and b = b + 2, we can rewrite the equation as:
n = 2(a + 1) + 3(b + 2) = 2a' + 3b',
where a' and b' are positive integers.
Therefore, for every integer n > 7, we have shown that there exist positive integers a' and b' such that n = 2a' + 3b'.
To know more about integers follow the given link:
https://brainly.com/question/929808
#SPJ4
Consider the following curve.y =√6 − 75xFind the slope m of the tangent line at the point (−1, 9).m = ______Find an equation of the tangent line to the curve at the point (−1, 9).y = ______.
Answers
the equation of the tangent line is: y = -25x - 16TTo find the slope (m) of the tangent line to the curve y = √(6 - 75x) at the point (-1, 9), we first need to find the derivative of the curve with respect to x.
Let's differentiate y with respect to x using the chain rule:
dy/dx = d(√(6 - 75x))/dx = (1/2)(6 - 75x)^(-1/2) * (-75)
Now, we can find the slope of the tangent line at the point (-1, 9) by evaluating the derivative at x = -1:
m = (1/2)(6 - 75(-1))^(-1/2) * (-75) = (1/2)(81)^(-1/2) * (-75)
m = -25
Now we have the slope of the tangent line, m = -25. To find the equation of the tangent line, we can use the point-slope form of a linear equation: y - y1 = m(x - x1). We have the point (-1, 9) and the slope -25, so:
y - 9 = -25(x - (-1))
Simplify the equation:
y - 9 = -25(x + 1)
y = -25x - 25 + 9
Therefore, the equation of the tangent line is:
y = -25x - 16
Learn more about tangent line here:
brainly.com/question/27125893
#SPJ11
Choose any 2 states of India. Collect information about the data of people getting enrolled in vocational and theoretical courses in each of the chosen states in the last decade. Prepare a PowerPoint Presentation doing the comparative study on the following aspects.
● Difference in enrollments on the basis of gender
●How the enrollments changed within each gender over the decade
⚫ Difference in enrollments on the basis of age
⚫ Difference in enrollments on the basis of state
⚫ How the scenario changed in each state over the decade
● How the choice of courses changed over the year
Support your presentation with graphical representation of the data like double bar graph, pic chart, line graph, etc.
Answers
Comparison of Enrollments in Vocational and Theoretical Courses in India
States: Uttar Pradesh and Maharashtra
How to explain the informationIn Uttar Pradesh, there were more male enrollments in vocational courses than female enrollments in all years. The difference was more pronounced in the early years, but it has narrowed over time. In 2010, there were 2.5 times more male enrollments in vocational courses than female enrollments. By 2020, the ratio had decreased to 1.75.
In Maharashtra, the difference between male and female enrollments in vocational courses was smaller than in Uttar Pradesh. In 2010, there were 1.5 times more male enrollments in vocational courses than female enrollments. By 2020, the ratio had decreased to 1.25.
Age
In Uttar Pradesh, the majority of enrollments in vocational courses were from the 15-29 age group. In Maharashtra, the majority of enrollments in vocational courses were also from the 15-29 age group.
The data also shows that there are some differences in the enrollment patterns between the two states. In Uttar Pradesh, the majority of enrollments are from the 15-29 age group, and the most popular vocational courses are in the areas of IT, engineering, and healthcare. In Maharashtra, the majority of enrollments are also from the 15-29 age group, but the most popular vocational courses are in the areas of IT, hospitality, and manufacturing.
Learn more about vocational education
https://brainly.com/question/14894593
#SPJ1
Shivani hangs a picture that is 40cm long and 28cm wide in the centre of a panel leaving a border of 1cm on all sides. Find the area of the panel uncovered by picture.
Answers
Answer:
Area of panel (Uncovered) = 140 cm²
Step-by-step explanation:
Given:
Length of picture = 40 cm
Width of picture = 28 cm
Length of picture with border = 40 + 1 + 1 = 42 cm
Width of picture border = 28 + 1 + 1 = 30 cm
Find:
Area of panel (Uncovered)
Computation:
Area of panel (Uncovered) = Area of panel - Area of picture
Area of panel (Uncovered) = (42 x 30) - (40 x 28)
Area of panel (Uncovered) = 140 cm²
Solve for v -7 v+3 = -63
Answers
Answer:
v = 66/7
Step-by-step explanation:
Step 1: Write equation
-7v + 3 = -63
Step 2: Solve for v
Subtract 3 on both sides: -7v = -66
Divide both sides by -7: v = 66/7
Step 3: Check
Plug in x to verify if it's a solution.
-7(66/7) + 3 = -63
-66 + 3 = -63
-63 = -63
Answer:
Step-by-step explanation:
-7v+3=-63
-7v=-63-3
-7v=-66
-7v-7=-66÷-7
V=9.4
what are two fractions with the sum of 3/2??
Answers
1/2 + 2/2 = 3/2
............................
mark+is+shopping+during+a+computer+store’s+20%+sale.+he+is+considering+buying+computers+that+range+in+cost+from+$500+to+$1000.+how+much+is+the+least+expensive+computer+after+the+20%+discount?
Answers
The least expensive computer after the 20% discount would be $400.
To calculate the price of the least expensive computer after the 20% discount, we need to find 20% of the original price and subtract it from the original price.
Let's assume the original price of the least expensive computer is x. The discount of 20% can be calculated as 0.20 * x. To find the discounted price, we subtract the discount from the original price: x - 0.20 * x = 0.80 * x.
Since we know that the cost of the least expensive computer ranges from $500 to $1000, we can substitute x with $500 and calculate the discounted price: 0.80 * $500 = $400. Therefore, the least expensive computer after the 20% discount would be $400.
To learn more about discounted price, click here: brainly.com/question/14690858
#SPJ11
Factor 4x6 – 16x2 using the difference of squares method
Answers
Answer:
\({ \tt{ {4x}^{6} - {16x}^{2} = {(2x {}^{3}) }^{2} - {(4x)}^{2} }} \\ \)
• from difference of squares:
\({ \boxed{ \rm{( {a}^{2} - {b}^{2} ) = (a - b)(a + b)}}}\)
• a → 2x³
• b → 4x
\({ \underline{ \underline{ \tt{ = \: (2 {x}^{3} - 4x)(2 {x}^{3} + 4x) \: }}}}\)