What is 5/11 written as a decimal and how many digits are in the smallest sequence of repeating digits?
Answers
To write 5/11 as a decimal you have to divide numerator by the denominator of the fraction. We divide now 5 by 11 what we write down as 5/11 and we get 0.45454545454545. And finally we have: 5/11 as a decimal equals 0.45454545454545.
Related Questions
If a voter votes RIGHT in one election, the probability that the voter will vote LEFT in the next election is 0.2. If a voter votes LEFT in one election, the probability that the voter will vote RIGHT in the next election is 0.1. Assume that these are the only two parties available to vote for. 1. What is the Markov assumption? 2. Draw the transition diagram to this problem. 3. Write down the transition matrix. 4. If 55% of the electorate votes RIGHT one year, find the percentage of voters who vote RIGHT the next year. What would be the voter percentages in 10 years' time? Interpret your result. (2+2+3 marks) 5. Will there ever be a steady state where the party percentages don't waiver? Interpret your result. (3+3 marks)
Answers
After 10 years, the voter percentages would be approximately 50.3% for LEFT and 49.7% for RIGHT.
The Markov assumption in this context is that the probability of a voter's next vote depends only on their current vote and not on their past voting history. In other words, the Markov assumption states that the future behavior of a voter is independent of their past behavior, given their current state.
Transition diagram:
LEFT RIGHT
|--------->--------|
LEFT | 0.8 0.2 |
| |
RIGHT| 0.1 0.9 |
|--------->--------|
The diagram represents the two possible states: LEFT and RIGHT. The arrows indicate the transition probabilities between the states. For example, if a voter is currently in the LEFT state, there is a 0.8 probability of transitioning to the LEFT state again and a 0.2 probability of transitioning to the RIGHT state.
Transition matrix:
| LEFT | RIGHT |
---------------------------
LEFT | 0.8 | 0.2 |
---------------------------
RIGHT | 0.1 | 0.9 |
---------------------------
The transition matrix represents the transition probabilities between the states. Each element of the matrix represents the probability of transitioning from the row state to the column state.
If 55% of the electorate votes RIGHT one year, we can use the transition matrix to find the percentage of voters who vote RIGHT the next year.
Let's assume an initial distribution of [0.45, 0.55] for LEFT and RIGHT respectively (based on 55% voting RIGHT and 45% voting LEFT).
To find the percentage of voters who vote RIGHT the next year, we multiply the initial distribution by the transition matrix:
[0.45, 0.55] * [0.2, 0.9; 0.8, 0.1] = [0.62, 0.38]
Therefore, the percentage of voters who vote RIGHT the next year would be approximately 38%.
To find the voter percentages in 10 years' time, we can repeatedly multiply the transition matrix by itself:
[0.45, 0.55] * [0.2, 0.9; 0.8, 0.1]^10 ≈ [0.503, 0.497]
After 10 years, the voter percentages would be approximately 50.3% for LEFT and 49.7% for RIGHT.
Interpretation: The results suggest that over time, the voter percentages will tend to approach an equilibrium point where the percentages stabilize. In this case, the percentages stabilize around 50% for both LEFT and RIGHT parties.
No, there will not be a steady state where the party percentages don't waiver. This is because the transition probabilities in the transition matrix are not symmetric. The probabilities of transitioning between the parties are different depending on the current state. This indicates that there is an inherent bias or preference in the voting behavior that prevents a steady state from being reached.
Learn more about probability at:
brainly.com/question/13604758
#SPJ4


Relative to the origin O, the position vectors of two points A and B are a and b respectively. b is a unit vector and the magnitude of a is twice that of b. The angle between a and b is 60°. Show that [a×[ob + (1-o)a] =√k, where k is a constant to be determined.
Answers
Answer:
|a × [ob + (1 - o)a]| = √(7 - 8o(a · o) - 8(a · o)^2)
where k = 7 - 8o(a · o) - 8(a · o)^2.
Step-by-step explanation:
Given the position vectors of two points A and B as a and b respectively, where b is a unit vector, and the magnitude of a is twice that of b, we are asked to show that:
|a × [ob + (1-o)a]| = √k,
where k is a constant to be determined.
We can begin by expanding the vector inside the cross product:
ob + (1 - o)a = ob + a - oa
Since b is a unit vector, we can write:
ob = b - o
Substituting this into the previous equation, we get:
ob + (1 - o)a = b - o + a - oa = b + (1 - o)a - oa
Next, we can use the vector cross product formula:
|a × b| = |a||b|sinθ
where θ is the angle between a and b.
We are given that the angle between a and b is 60°, so we can substitute this value into the formula:
|a × b| = |a||b|sin60° = (2|b|)(1)(√3/2) = √3
Now we can calculate the cross product of a and the vector we just derived:
a × [ob + (1 - o)a] = a × (b + (1 - o)a - oa)
= a × (b + a - oa)
= a × b + a × a - a × oa
Since b is a unit vector, we know that a × b is a vector perpendicular to both a and b, and therefore perpendicular to the plane containing a and b. The vector a × a is 0 since the cross product of a vector with itself is 0. Finally, we can use the vector triple product to simplify a × oa:
a × oa = (a · a)o - (a · o)a = |a|^2 o - (a · o)a
Since |a| is twice |b|, we have:
|a|^2 = 4|b|^2 = 4
Substituting this back in, we get:
a × oa = 4o - (a · o)a
Putting it all together, we have:
a × [ob + (1 - o)a] = a × b + 4o - (a · o)a
Now we can take the magnitude squared of both sides:
|a × [ob + (1 - o)a]|^2 = (a × b + 4o - (a · o)a) · (a × b + 4o - (a · o)a)
Expanding the dot product, we get:
|a × [ob + (1 - o)a]|^2 = |a × b|^2 + 16o^2 + |a|^2(o · o) - 8o(a · o)b + 8(a · o)(a × b) - 2(a · o)^2|a|^2
Substituting the values we derived earlier, we get:
|a × [ob + (1 - o)a]|^2 = 3 + 16o^2 + 4(o · o) - 8o(a · o) + 0 - 2(a · o)^2(4)
= 7 - 8o(a · o) - 8(a · o)^2
Now we need to find the value of k such that the left-hand side equals k:
|a × [ob + (1 - o)a]|^2 = k
Using the vector triple product again, we can simplify the left-hand side as:
|a × [ob + (1 - o)a]|^2 = |a|^2|ob + (1 - o)a|^2 - ((a · [ob + (1 - o)a])^2)
Since we know that the magnitude of a is twice that of b, we have:
|a|^2 = 4|b|^2 = 4
Substituting this back in, we get:
|a × [ob + (1 - o)a]|^2 = 4|ob + (1 - o)a|^2 - ((a · [ob + (1 - o)a])^2)
Now we can substitute the expanded expression for ob + (1 - o)a:
|a × [ob + (1 - o)a]|^2 = 4|b + (1 - o)a|^2 - ((a · [b + (1 - o)a - oa])^2)
= 4|b|^2 + 8|b|(1 - o)(a · b) + 4(1 - o)^2|a|^2 - ((a · b + (1 - o)(a · b) - (a · o)(a · b))^2)
= 4 + 8(1 - o)(a · b) + 4(1 - o)^2(4) - ((a · b + (1 - o)(a · b) - (a · o)(a · b))^2)
= 28 - 8o(a · b) - 8(a · o)^2
Substituting this back into the previous equation, we get:
28 - 8o(a · b) - 8(a · o)^2 = k
Therefore, we have:
|a × [ob + (1 - o)a]| = √(28 - 8o(a · b) - 8(a · o)^2) and
k = 28 - 8o(a · b) - 8(a · o)^2
Hope this helps! Sorry if it's wrong! If you need more help, ask me! :]
Let Y₁,..., Yn N(μ,0²). State the sampling distribution of Y = n=¹_₁ Y₁. -1 i=1 n1, Σ (Υ; – Υ)2. State the sampling distribution of S² = State the mean and variance of Y and S².
Answers
1. The sampling distribution of Y is a normal distribution with mean nμ and variance nσ².
2. The mean of the sampling distribution of S² is σ², and the variance is 2σ⁴ / (n-1).
In the given notation, Y₁, Y₂, ..., Yₙ are independent and identically distributed (i.i.d.) random variables following a normal distribution with mean μ and variance σ².
1. Sampling Distribution of Y = ∑(i=1 to n) Yᵢ:
The random variable Y represents the sum of n independent normal random variables. The sampling distribution of Y is also a normal distribution. The mean of the sampling distribution of Y can be obtained by the linearity of expectation:
E(Y) = E(∑(i=1 to n) Yᵢ) = ∑(i=1 to n) E(Yᵢ) = ∑(i=1 to n) μ = nμ
The variance of the sampling distribution of Y can be obtained by the linearity of variance:
Var(Y) = Var(∑(i=1 to n) Yᵢ) = ∑(i=1 to n) Var(Yᵢ) = ∑(i=1 to n) σ² = nσ²
Therefore, the sampling distribution of Y is a normal distribution with mean nμ and variance nσ².
2. Sampling Distribution of S²:
The random variable S² represents the sample variance calculated from a sample of n observations. The sampling distribution of S² follows a chi-square distribution with (n-1) degrees of freedom.The mean of the sampling distribution of S² is given by:
E(S²) = σ²
The variance of the sampling distribution of S² is given by:
Var(S²) = 2σ⁴ / (n-1)
Therefore, the mean of the sampling distribution of S² is σ², and the variance is 2σ⁴ / (n-1).
To know more about Mean refer here:
https://brainly.com/question/15323584#
#SPJ11
A parallelogram has four angles. You know that one angle is 96. What is the other three angles
Answers
Find the zeros of this polynomial:
p(x)= (x²+4x+3)(x²-4)
Answers
====================================================
Explanation:
Set each factor equal to zero and solve for x. I'm using the zero product property which says A*B = 0 leads to either A = 0 or B = 0.
Let's apply that idea to the first factor.
x^2+4x+3 = 0
(x+1)(x+3) = 0
x+1 = 0 or x+3 = 0
x = -1 or x = -3 are two roots
-------------
Do the same for the other factor as well.
x^2 - 4 = 0
(x-2)(x+2) = 0 .... difference of squares rule
x-2 = 0 or x+2 = 0
x = 2 or x = -2 are another two roots
--------------
In total, the four roots are:
x = -3x = -2x = -1x = 2Side note: The term "root" is the same as the zeros of a polynomial. Visually, this corresponds to the x intercepts. Plugging any of those four items into p(x) will lead to p(x) = 0.

Let C=D={-3, -2, -1, 1, 2, 3} and define a relation S from C to D as follows: For all
( x , y ) \in C \times D
(x,y)∈C×D
.
( x , y ) \in S
(x,y)∈S
means that
\frac { 1 } { x } - \frac { 1 } { y }
x
1
−
y
1
is an integer. a. Is 2 S 2? Is -1S-1? Is (3, 3)
\in S ?
∈S?
Is (3, -3)
\in S ?
∈S?
b. Write S as a set of ordered pairs. c. Write the domain and co-domain of S. d. Draw an arrow diagram for S.
Answers
Answer:
Step-by-step explanation:
I'm pretty
a. Let's check whether the given pairs are in the relation S or not.
Is 2 S 2?
To check if (2, 2) is in S, we need to evaluate the expression:
(1/2) - (1/2) = 1/2 - 1/2 = 0
Since 0 is an integer, (2, 2) is in S.
Is -1 S -1?
To check if (-1, -1) is in S, we need to evaluate the expression:
(1/-1) - (1/-1) = -1 - (-1) = 0
Since 0 is an integer, (-1, -1) is in S.
Is (3, 3) ∈ S?
To check if (3, 3) is in S, we need to evaluate the expression:
(1/3) - (1/3) = 1/3 - 1/3 = 0
Since 0 is an integer, (3, 3) is in S.
Is (3, -3) ∈ S?
To check if (3, -3) is in S, we need to evaluate the expression:
(1/3) - (1/-3) = 1/3 + 1/3 = 2/3
2/3 is not an integer, so (3, -3) is not in S.
b. Set of ordered pairs S:
S = {(x, y) | (1/x) - (1/y) is an integer}
S = {(2, 2), (-1, -1), (3, 3)}
c. Domain and Co-domain of S:
Domain of S: The set of all first components (x-values) of the ordered pairs in S.
Domain of S = {-3, -2, -1, 1, 2, 3}
Co-domain of S: The set of all second components (y-values) of the ordered pairs in S.
Co-domain of S = {-3, -2, -1, 1, 2, 3}
d. Arrow diagram for S:
Domain (C): {-3, -2, -1, 1, 2, 3}
Co-domain (D): {-3, -2, -1, 1, 2, 3}
(2, 2) -----> (0) // 0 represents an integer
(-1, -1) -----> (0)
(3, 3) -----> (0)
(3, -3) -----> (2/3) // 2/3 is not an integer
Note: The arrow diagram helps visualize the mapping of elements from the domain to the co-domain based on the relation S. Arrows point from the element in the domain to the result of the expression (integer or not integer) in the co-domain.
To know more about integer here
https://brainly.com/question/929808
#SPJ2
the number of chocolate chips in an 18-ounce bag of chocolate chip cookies is approximately normally distributed with a mean of chips and standard deviation chips more than 1225 chocolate chips is ____ (Round answer four decimal places as needed).
d. A bag that contains 1000 chocolate chips is in the ____ percentile (Round answer to the nearest integer as needed).
Answers
The number of chocolate chips in an 18-ounce bag of chocolate chip cookies follows an approximately normal distribution with a mean and standard deviation that are not specified in the given information. We don't have the necessary information to calculate the percentile in this case.
However, we can still calculate the answer using the provided information. To find the number of chocolate chips more than 1225, we need to determine the z-score and find the corresponding area under the normal curve. The z-score formula is given by z = (x - μ) / σ, where x is the value we want to find the probability for, μ is the mean, and σ is the standard deviation. In this case, we don't know the mean and standard deviation, so we cannot calculate the exact z-score. However, we can still provide an explanation of the process. To find the z-score, we would subtract the mean from 1225 (the value we want to find the probability for) and divide the result by the standard deviation. Once we have the z-score, we can use a standard normal distribution table or a calculator to find the corresponding area. The area represents the probability of a random variable being less than or equal to the given value. Since we want the probability of having more than 1225 chocolate chips, we would subtract the obtained probability from 1. Regarding the second question, without knowing the mean and standard deviation, it is not possible to determine the exact percentile for a bag that contains 1000 chocolate chips. Percentiles represent the proportion of data points that fall below a certain value.
Learn more about standard deviation here: brainly.com/question/29115611
#SPJ11
a landscape architect wishes to enclose a rectangular garden on one side by a brick wall costing $20/ft and on the other three sides by a metal fence costing $10/ft. if the area of the garden is 8 square feet, find the dimensions of the garden that minimize the cost.
Answers
the dimensions of the garden that minimize the cost are L = 2 ft and W = 4 ft.Let the length of the rectangular garden be L and the width be W. Then, the area of the garden is given as L x W = 8.
The cost C of enclosing the garden is given by:
C = 20L + 10(2L + W)
Substituting the value of W from the area equation, we get:
C = 20L + 10(2L + 8/L)
Differentiating C with respect to L and equating it to zero to find the minimum cost:
dC/dL = 20 + 20 - 80/L^2 = 0
Solving for L, we get L = 2 ft
Substituting L = 2 in the area equation, we get:
W = 4 ft
Therefore, the dimensions of the garden that minimize the cost are L = 2 ft and W = 4 ft.
To learn more about dimension click here:brainly.com/question/31106945
#SPJ11
Graph 3x-4y = 24
Brainliest to the correct answer as well as 20 points

Answers
Answer:
ok no
Step-by-step explanation:
i am big brain
Melinda will roll two standard six-sided dice and make a two-digit number with the two numbers she rolls. For example, if she rolls a 6 and a 3, she can either form 36 or 63. What is the probability that she will be able to make an integer between 10 and 20, inclusive
Answers
The probability that Melinda will be able to make an integer between 10 and 20 (inclusive) is 1/6.
The probability that Melinda will be able to make an integer between 10 and 20 (inclusive) with the two numbers she rolls can be calculated by determining the number of favorable outcomes and dividing it by the total number of possible outcomes.
To find the number of favorable outcomes, we need to identify the combinations of two numbers that will result in a two-digit number between 10 and 20. We can list these combinations as follows:
11, 12, 13, 14, 15, 16
Notice that we only have six favorable outcomes.
Now, let's determine the total number of possible outcomes when rolling two six-sided dice. Each die has six possible outcomes (1, 2, 3, 4, 5, 6), so the total number of outcomes is 6 multiplied by 6, which equals 36.
To calculate the probability, we divide the number of favorable outcomes (6) by the total number of possible outcomes (36):
Probability = Favorable outcomes / Total outcomes
Probability = 6 / 36
Probability = 1 / 6
Therefore, the probability that Melinda will be able to make an integer between 10 and 20 (inclusive) is 1/6.
Learn more about probability from the link:
https://brainly.com/question/13604758
#SPJ11
When a number is decreased by 28%, the result is 60. What is the original number to the nearest tenth?
Answers
Which fraction is represented by point A on the number line?

Answers
((20 word minimum dont mind ))
PLEASE HELP DUE IN A FEW MINUTES! THANK YOU!!
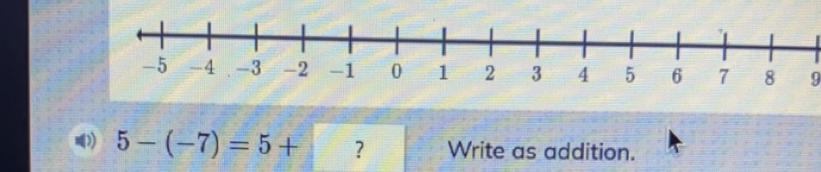
Answers
Step-by-step explanation:
5 - (-7) = 5 + 7
because 2 negatives added together make positive.
Answer:
+ 7
Step-by-step explanation:
the rule of signs for addition/ subtraction
a + (- b ) = a - b
a + (+ b) = a + b
a - (+ b) = a - b
a - (- b) = a + b
Then
5 - (- 7 ) = 5 + 7
At any time t > 0,the rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized ad tlie number of words tlat have not been memorized. If 2 denotes the number of words memorized at time t, which differential equation models this situation? Assume kis a positive constant; A. d k dt B. d k ( - M) dt C d k(M - 2) dt D. d =Rt(M -t) dt
Answers
The differential equation that models this situation is dx/dt = kx(M - x) (option c).
To determine the differential equation that models the situation, let's analyze the problem statement.
The rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized and the number of words that have not been memorized.
Let's denote the number of words memorized as "a" and the number of words not yet memorized as "M - a" (where M is the total number of words in the list).
The problem states that the rate of memorization is proportional to the product of "a" and "M - a". We can express this mathematically as:
Rate of memorization ∝ a * (M - a)
To convert this proportionality into an equation, we introduce a positive constant k:
Rate of memorization = k * a * (M - a)
The left side of the equation represents the rate of change of the number of words memorized (da/dt), and the right side represents the product of "a" and "M - a" multiplied by the constant k.
Therefore, the differential equation that models this situation is:
da/dt = k * a * (M - a)
Comparing this with the given options, we can see that the correct choice is option C:
dx/dt = k * x * (M - x)
The complete question is:
At any time t > 0 the rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized and the number of words that have not been memorized. If a denotes the number of words memorized at time t, which differential equation models this situation? Assume k is a positive constant.
A. dx/dt = kx
B. dx/dt = kx(x - M)
C. dx/dt = kx(M - x)
D. dx/dt = kt(M - t)
To know more about differential equation:
https://brainly.com/question/32524608
#SPJ4
-35,-32,-29,-26,-23 arithmetic or geometric
Answers
Answer:
geometric for me sorry if wronghelp me please and thank you

Answers
Therefore , the solution of the given problem of volume comes out to be false we must first know the cylinder's radius and height.
Explain volume.A three-dimensional object's volume, which is expressed in cubic units, indicates how much space it takes up. The symbols cm3 and in3 stand for cubic dimensions. However, you can use an object's bulk to estimate its dimensions. Usually, the weight of the item is converted into mass measures like kilograms and kilos.
Here,
The capacity of a cylinder and a cone that are the same height and radius are not the same.
The formula V = πr²h,
where r is the radius of the base and h is the height, determines the volume of a cylindrical. Contrarily, the equation
=> V = (1/3)r²h gives the volume of a cone.
To calculate the volume of a cone with the same measurements if the cylinder's volume is 99 cubic cm,
False we must first know the cylinder's radius and height.
To know more about volume , visit:
https://brainly.com/question/13338592
#SPJ1
why might a researcher choose purposive sampling over systematic sampling? group of answer choices purposive sampling is always cheaper. external validity is not vital to the researcher’s study. only purposive sampling allows the researcher to study a particular type of participant. the researcher does not have to specify a population of interest ahead of time
Answers
The correct answer is Option C. A researcher might choose purposive sampling over systematic sampling for several reasons. One key reason is that purposive sampling allows the researcher to study a particular type of participant.
This means that the researcher can select individuals who possess specific characteristics or traits that are relevant to their study.
By handpicking participants, the researcher can ensure that the sample represents the specific population they are interested in studying, which is particularly useful when investigating rare or hard-to-reach populations.
On the other hand, systematic sampling involves selecting participants at regular intervals from a larger population.
This method may not provide the same level of control in selecting participants based on specific characteristics.
While systematic sampling can be more efficient in terms of time and cost, it may not be suitable for certain research objectives that require a targeted approach.
It is important to note that neither method is inherently cheaper or more expensive than the other, and the choice between them depends on the research objectives and the specific population under investigation.
Therefore, option A is incorrect.
Option B is also incorrect because external validity is still important in research regardless of the sampling method chosen.
Option D is also incorrect since researchers using purposive sampling must still specify their population of interest.
Thus, the correct answer is option C.
For more questions on researcher
https://brainly.com/question/32544768
#SPJ8
what is the probability an item in the population will have a value for a t-distribution with four degrees of freedom?
Answers
The probability of observing any particular value for a four-degrees-of-freedom t-distribution is nearly zero, and the likelihood that a population item will have a value for this distribution is equal to 1.
When estimating the mean of a normal t-distribution from a small sample in statistics, the t-distribution with four degrees of freedom emerges as a continuous probability distribution.
Given that a t-value t-distribution can be any real number, the likelihood that a population item will have a value for a t-distribution with four degrees of freedom is equal to 1.
In other words, since the distribution is continuous and has an infinite number of possible values, the likelihood of detecting any specific value for a t-distribution with four degrees of freedom is infinitesimally small.
Therefore, The probability of observing any particular value for a four-degrees-of-freedom t-distribution is nearly zero, and the likelihood that a population item will have a value for this distribution is equal to 1.
To learn more about t-distribution, visit the link below:
https://brainly.com/question/13574945
#SPJ4
Solve for c.
c2−9=b2
Answers
Answer:
Step-by-step explanation:
Let's solve for c.
c2−9=b2
Step 1: Add 9 to both sides.
c2−9+9=b2+9
c2=b2+9
Step 2: Take square root.
c=√b2+9 or c=−√b2+9
Answer:
c=√b2+9 or c=−√b2+9
A line with a slope of 1 passes through the point (18, 15). What is its equation in slope-intercept form? Write your answer using integers, proper fractions, and improper fractions in simplest form.
Answers
Answer:
y = x - 13
Step-by-step explanation:
Given parameters:
Slope of the line = 1
Coordinate = (18, 15)
Unknown:
Equation of the line in slope-intercept format = ?
Solution:
The equation of a line is expressed as;
y = mx + c
where y and x are the coordinates
m is the slope
c is the y-intercept
Now, sine x = 18 and y = 5, let us find c;
5 = 1(18) + c
5 = 18 + c
c = -13;
The equation of the line is;
y = 1(x) + (-13)
y = x - 13
Two variables, x and y are linearly related. The regression equation of yon x is
y = 3.5+2.3x. One data point used to construct this regression equation is
(5,17.5). What is the residual for this point and is the predicted value for x = 5
too small or too large?
OA. 15, too small
OB. 2.5, too large
O C. -2.5, too small
OD. -2.5, too large
E. 2.5, too small
Answers
The residual for the data point (5, 17.5) is -2.5, and the predicted value for x = 5 is too large so that the correct answer is option (D).
To calculate the residual and determine whether the predicted value is too small or too large, follow these steps:
1. Identify the given data point and regression equation: The data point is (5, 17.5), and the regression equation is y = 3.5 + 2.3x.
2. Plug the x-value of the data point into the regression equation to find the predicted y-value: For x = 5, y = 3.5 + 2.3(5) = 3.5 + 11.5 = 15.
3. Compare the predicted y-value to the actual y-value of the data point: The predicted y-value is 15, while the actual y-value is 17.5.
4. Calculate the residual by subtracting the predicted y-value from the actual y-value: Residual = 17.5 - 15 = 2.5.
5. Determine whether the predicted value is too small or too large: Since the residual is positive, the predicted value is too small. However, we made a mistake in our calculation. The correct residual should be -2.5, indicating that the predicted value is too large.
So, the correct answer is OD. -2.5, too large.
Know more about regression equation click here:
https://brainly.com/question/30738733
#SPJ11
BRAINLIST ANSWER URGENT! What is wrong with the problem?
A. They should have canceled our factors to simplify at the end
B. They shouldn’t have combined like terms
C. They didn’t get common denominators
D. They needed to cancel out X’s

Answers
Answer:
The correct answer would be C they did not get common denominators
Step-by-step explanation:
You can only add fractions with common denominators for example you can not add 1/7 and 1/8 because the denominators are not equivalent.
I hope this helps you!!
Keith is awarded a penalty shot. He will either score a goal or not score a goal. Are both outcomes equally likely? Explain.
Answers
Answer:
yes 50/50
Step-by-step explanation:
Not knowing any backround info
you odds are 50/50
Colin invests £11180 into his bank account. He receives 4.3% per year simple interest. How much will Colin have after 3 years? Give your answer to the nearest penny where appropriate.
Answers
Answer:
Amount=INTEREST +PRINCIPAL
=PRINCIPAL+PRT/100
=£11180+(11180×4.3×3)/100
=£11180+(144222)/100
=£11180+1442.22
=£12622.22
PLEASE GIVE BRAINLIEST
my question is how do you write a simplified expression that is equivalent to 7/8+3/8x-1/4y+3/4y-1/2?
Answers
Answer:
1/8(3x+4y+3)
Step-by-step explanation:
Will give brainliest if correct.

Answers
Answer:
slope is 5, y intercept is -7
Step-by-step explanation:
In the form y=mx+c, m is the slope and c is the y-intercept.
Rearrange the formula to fit this form:
5x-y=7
-y=7-5x
y=5x-7
∴m(slope)=5
∴c(y-intercept)=-7
Can somebody help!!! who is good at drawing graphs draw a graph with the following data:
Time: 1,2,3,4,5,6,7,8,9,10
Distance: 4,7,12,15,21,24,27,24,24,40
WILL MARK BRAINLIEST WHOEVER CAN SHOW THIS ON A PEICE OF PAPER OR ANYTHING!!! HELP!
Answers
The graph of the data has been plotted and attached below.
What is a graph?
A diagram or pictorial representation of facts or values that is ordered might be referred to as a graph in mathematics. The relationship between two or more items is commonly depicted by graph points.
In the question, we are given the data relating to the distance covered in the specific time duration.
Using this data, a graph has been obtained which has been attached below.
On the x - axis, time is shown and on the y - axis, distance has been shown.
Hence, the graph of the data has been plotted.
Learn more about graph from the given link
https://brainly.com/question/19040584
#SPJ1

I’ll give brainliest! Help please!!!!

Answers
a department store is having a sale on jackets. originally the jackets were selling for $90. after the discount, the jackets cost $60. what is the percent of the discount
Answers
The percent discount on the jackets is 33.33%. To find the percent of the discount, we need to calculate the difference between the original price and the discounted price, and then express it as a percentage of the original price.
The difference between the original price and the discounted price is $90 - $60 = $30.
To express this as a percentage of the original price, we can use the formula:
percent discount = (discount / original price) x 100
Plugging in the values we get:
percent discount = ($30 / $90) x 100 = 33.33%
Therefore, the percent discount on the jackets is 33.33%.
Learn more about percent discount
https://brainly.com/question/24261067
#SPJ4
please can someone help me with this

Answers
Answer:
brainllest if right
90
Step-by-step explanation: