what is a paired t-test? question 4select one: a. given a single numeric variable, a test for that variable's population mean b. given a single categorical variable, a test for that variable's population mean c. given a two numeric variables, a test for the difference of those variable's population means d. given a two numeric variables measured on the same or very similar units, a test for the mean of the differences between those variables
Answers
d. A paired t-test is a statistical test used to determine if there is a significant difference between the means of two related or paired samples.
It is used when two numeric variables are measured on the same or very similar units and the goal is to test for the mean of the differences between those variables. For example, it could be used to test whether a new drug treatment is significantly more effective than a placebo treatment, by measuring the difference in response between the same individuals receiving the two treatments. The paired t-test is also sometimes called a dependent samples t-test or a matched pairs t-test.
To know more about T-test,
https://brainly.com/question/29443181
#SPJ11
Related Questions
which number produces an irrational answer when added to 3/4
Answers
Answer
pi.
Step-by-step explanation:
If you add pi (3.14) to 3/4, you will get an irrational answer.
Can someone check all my answers? thanks

Answers
Answer:
By the looks of it you got them all, correct!
Your handwriting is quite nice by the way!
Step-by-step explanation:
Have a good day!
Answer:
i don't know the answer but can you help me with a question
Two meshing standard spur gears have 20 degrees of pressure angle (0). Their diametral pitch (pa) is 4. The pinion has 28 teeth (NP) while the gear has 56 teeth (Ng). Determine the nominal center distance C. If the center distance is increased by 0.15 inch, find the new pressure angle Pnew .
Answers
The nominal center distance between the gears is 3.5 inches, and the new pressure angle is approximately 19.82 degrees when the center distance is increased by 0.15 inch.
To determine the nominal center distance between two meshing spur gears, we use the formula \(C = \frac{{NP + NG}}{{2 \cdot P_a}}\), where \(NP\) and \(NG\) represent the number of teeth on the pinion and gear, respectively, and \(P_a\) is the diametral pitch.
In this case, with \(NP = 28\), \(NG = 56\), and \(P_a = 4\), substituting the values into the formula gives \(C = \frac{{28 + 56}}{{2 \cdot 4}} = 3.5\) inches.
If the center distance is increased by 0.15 inch, the new center distance becomes \(C_{\text{new}} = C + 0.15\) inches.
To find the new pressure angle \(P_{\text{new}}\), we use the formula \(P_{\text{new}} = \tan^{-1}\left(\frac{{\tan(P_a) \cdot C_{\text{new}}}}{{C}}\right)\).
Substituting the values, we find \(P_{\text{new}} = \tan^{-1}\left(\frac{{\tan(20^\circ) \cdot 3.65}}{{3.5}}\right) \approx 19.82^\circ\).
Therefore, the nominal center distance \(C\) is 3.5 inches, and the new pressure angle \(P_{\text{new}}\) is approximately 19.82 degrees when the center distance is increased by 0.15 inch.
Learn more about Distance click here :brainly.com/question/26550516
#SPJ11
A cubic polynomial with a critical point at x=2, an inflection point at (1,4), and a leading coefficient of 1
Answers
If a critical point at x=2, an inflection point at (1,4), and a leading coefficient of 1, the final formula for the cubic polynomial is f(x) = x³ - 3x² + 12x - 6.
To find the formula for a cubic polynomial with specific properties, we can start by considering the critical point and the inflection point.
Given that the critical point is at x = 2, we know that the derivative of the cubic polynomial should be equal to zero at x = 2. This means that the slope of the polynomial at x = 2 is zero. Taking the derivative of the cubic polynomial, we have:
f'(x) = 3ax² + 2bx + c.
Setting this equal to zero and substituting x = 2, we get:
3a(2)² + 2b(2) + c = 0.
12a + 4b + c = 0.
Now, let's consider the inflection point at (1,4). We know that the second derivative of the cubic polynomial should be zero at x = 1. Taking the second derivative, we have:
f''(x) = 6ax + 2b.
Setting this equal to zero and substituting x = 1, we get:
6a(1) + 2b = 0.
6a + 2b = 0.
Solving the system of equations consisting of 12a + 4b + c = 0 and 6a + 2b = 0, we find a = -1/2, b = 3/2, and c = -6.
Therefore, the formula for the cubic polynomial is:
f(x) = -1/2x³ + 3/2x² - 6x + d.
The leading coefficient is 1, so we have:
f(x) = x³ - 3x² + 12x + d.
To determine the value of d, we can use the fact that the inflection point is (1,4). Substituting x = 1 and y = 4 into the equation, we get:
4 = 1 - 3 + 12 + d.
4 = 10 + d.
d = -6.
Therefore, the final formula for the cubic polynomial is:
f(x) = x³ - 3x² + 12x - 6.
To learn more about cubic polynomial click on,
https://brainly.com/question/31418151
#SPJ4
Complete question is:
Find the formula for a cubic polynomial, ax³+bx²+cx+d, with a critical point at x=2, an inflection point at (1,4), and a leading coefficient of 1.
Whats 2(3/4n+8+1/4n-12)?
Answers
The result of the simplified form of the given expression; 2(3/4n+8+1/4n-12) is; 2n - 8.
What is the result of the simplification of the given expression?It follows from the task content that the result of the simplified form of the given expression is to be determined.
On this note, since the given expression is;
2 ( 3/4n + 8 + 1/4n - 12 )
Therefore, the given expression can be simplified by solving the parentheses first as follows;
2 ( 3/4n + 1/4n + 8 - 12 )
= 2 ( n - 4 )
= 2n - 8.
Hence, the simplified form of the given expression is; 2n - 8.
Read more on simplification of expressions;
https://brainly.com/question/14027225
#SPJ1
whats 25 times 80 times 96
Answers
Answer: 192,000
Step-by-step explanation:
..
25*80*96=192000
Three friends all live
on the same street that runs west to east. Beth
lives 5 blocks from Ann. Carl lives 2 blocks from
Beth. If the street is represented by a number
line and Ann's house is located at 0, what are the
possible locations for Carl's house? Assume that
each unit on the number line represents 1 block.
Answers
Answer:
Carl lives seven blocks away from Ann
Step-by-step explanation:
You start at Ann's house ( 0 ) 0+5+2=7
Beth is five blocks from Ann ( 5 )
Carl lives two blocks from Beth ( 2 )
Answer:
carl can be at 4 or 2
Step-by-step explanation:
what is the word used to describe a vector that always points toward the center of a circular path?
Answers
"Centripetal is the word used to describe a vector that always points toward the centre of a circular path."
The centripetal acceleration vector is an acceleration in the radial direction that is directed towards the centre of the circular line of motion. It runs perpendicular to the linear motion, or v.
The direction of the velocity shift for a ball travelling around a curve is in the direction of the curve's centre. Centripetal acceleration is the acceleration that is directed towards the centre of a curved or circular route.
Any force that changes the path of motion towards the centre of a circular motion is known as a centripetal force. The portion of the force that produces the centripetal force is the part that is perpendicular to the velocity.
To know more about vectors:
https://brainly.com/question/13590043
#SPJ4
The foot of a ladder is placed 18 feet from a wall. If the top of the ladder
rests 24 feet up on the wall, find the length of the ladder.
26 feet
27 feet
29 feet
O 30 feet
Answers
Answer:
I'm not sure
I think its 30 or 26
Step-by-step explanation:
Answer:
30 feet
Step-by-step explanation:
The ladder laying against the wall will create a right triangle.
The side lengths will be 18 and 24 and you will solve for the hypoteneuse which will be the length of the latter.
You can use the pythagorean theorm so
\(a^{2} +b^{2} =c^{2}\) so you plug in the values
\(18^{2}+24^{2} =c^{2} \\324+576=c^{2} \\900=c^{2} \\\sqrt{900} =\sqrt{c^{2} } \\30=c\)
a. Write in your own words a definition of a complex numbers and Modulusof the complex number. Support your answers with examples. (4 marks) b.Find the modulus of + mi (10 marks) c. Write the complex number 2 = ((2+ m) + 3i)in polar form (13 marks) 100+m
Answers
The complex number can be written in polar form as 2 + ((2+m) + 3i) = √(m² + 6m + 25)∠tan⁻¹(3/(2+m)).
What is complex number?
A complex number is obtained by adding real and imaginary numbers. Complex numbers have the formula a + ib and are usually symbolized by the symbol z. Here the numbers a and real are both. The value "a" is known as the real component and is denoted Re(z), while "b" is known as the imaginary part and is denoted Im(z). Also known as imaginary number, ib. Hero of Alexandria, a Greek mathematician, first used the idea of complex numbers in the first century when he tried to calculate the square root of a negative integer.
a. A complex number is a number that consists of a real part and an imaginary part, where the imaginary part is the real number multiplied by the imaginary unit "i", defined as the square root of -1. The modulus of a complex number is the distance between the starting point and the point representing the complex number on the complex plane. This can be calculated using the Pythagorean theorem. For example, the real part of the complex number z = 3 + 4i is 3 and the imaginary part is 4, and its modulus is √(3²+4²)=5.
b. Let z = a + bi be a complex number, where a and b are real numbers. The modulus of z is defined as |z| = √(a² + b²). Therefore, for the complex number z = 1 + 2i, the modulus is |z| = √(1² + 2²) = √5.
c. To write the complex number 2 = ((2+ m) + 3i) in polar form, we need to find the modulus and argument of the complex number. The modulus is |2 + ((2+m) + 3i)| = |4 + mi + 3i| = √(4² + (m+3)²) = √(m² + 6m + 25). The argument is given by tan⁻¹(Im/Re) = tan⁻¹(3/(2+m)), which gives us the angle that the complex number makes with the positive real axis. Therefore, the complex number can be written in polar form as 2 + ((2+m) + 3i) = √(m² + 6m + 25)∠tan⁻¹(3/(2+m)).
Learn more about complex number, by the following link
https://brainly.com/question/10662770
#SPJ4
What do you have to do to
determine which function increases faster when
looking at a table and a graph of two different
functions PLS SOMEONE HELP
Answers
To determine which function increases faster, we have to find the ratio = \(\frac{\triangle y}{\triangle x}\).
Rate of Change:
A rate of change describes how an output quantity changes relative to the change in the input quantity. The units on a rate of change are “output units per input units.”
The average rate of change between two input values is the total change of the function values (output values) divided by the change in the input values.
\(\frac{\triangle y}{\triangle x} = \frac{f(x_{2})-f(x_{1}) }{x_{2}-x_{1}}\)
How to determine:
Given the value of a function at different points, calculate the average rate of change of a function for the interval between two values \(x_{1}\) and \(x_{2}\).
Calculate the difference \(y_{2}-y_{1} = \triangle y\)Calculate the difference \(x_{2}-x_{1} = \triangle x\)Find the ratio \(\frac{\triangle y}{\triangle x}\)Hence the answer is to determine which function increases faster, we have to find the ratio = \(\frac{\triangle y}{\triangle x}\).
To learn more about functions click here https://brainly.com/question/25638609
#SPJ9
Cho A= [ -4;4] B= ( 1;7] Xác định A B
Answers
To find the intersection of A and B figure who has the bigger lower bounds and smaller upper bounds out of A and B.
The lower bound of A is -4 while the lower bound of B is (but not including) 1. So the lower bound will be (1.
The upper bound of A is 4 while the upper bound of B is 7. So the resulting upper bound will be 4].
Put these together and get (1,4].
Hope this helps :)
What is the value of n?
What is the value of n?

Answers
Answer:
42
Step-by-step explanation:
You get 42 by looking at the denominators 7 and 21. You times by 3 to get from 7 to 21, so you times 14 by 3 to get n, which is 42.
Answer:
42
Step-by-step explanation:
On the bottom 7 was multiplied by 3 so you would do the same to 14.
If x+6>2x+4, which of the following is NOT a possible value for x?
Answers
245
Step-by-step explanation:
b
Answer:56
Step-by-step explanation:
Find the indefinite integral. Check your work by differentiation. ∫6x(9−x)dx ∫6x(9−x)dx=__
Answers
Therefore, the indefinite integral of ∫6x(9−x)dx is \(27x^2 - 2x^3 + C\), where C is a constant.
To find the indefinite integral of ∫6x(9−x)dx, we can expand the expression and then integrate each term separately:
∫6x(9−x)dx = ∫\((54x-6x^2)dx\)
Using the power rule for integration, we have:
∫54xdx =\((54/2)x^2 + C_1\)
\(= 27x^2 + C_1\)
∫\(-6x^2dx = (-6/3)x^3 + C_2 \\= -2x^3 + C_2\)
Combining the results, we have:
∫6x(9−x)dx\(= 27x^2 - 2x^3 + C\)
To check our work, we can differentiate the obtained result:
\(d/dx (27x^2 - 2x^3 + C) = 54x - 6x^2\)
which matches the original integrand 6x(9−x).
To know more about indefinite integral,
https://brainly.com/question/31969670
#SPJ11
Question 7: Luna has consumed 900 calories so far today. She has also burned 500 calories in dance class. She wants to keep her daily calorie total to 1,500 calories per day. How many calories does she have left to consume for the day? Is 1,200 a viable solution to this problem?
No; 1,200 is more than the 500 she burned dancing.
No; 1,200 will cause her to exceed 1,500.
Yes; 1,200 is less than 1,500.
Yes; 1,100 is less than 1,500.
Answers
1,200 is not a viable solution to this problem as B.
No; 1,200 will cause her to exceed 1,500
How to calculate the value?It should be noted that Luna has consumed 900 calories so far today and has also burned 500 calories in dance class.
Therefore, the amount left will be:
= 1500 - (900 - 500)
= 1500 - 400
= 1100
Therefore, 1,200 is not a viable solution to this problem
Learn more about calories on:
brainly.com/question/1178789
#SPJ1
The variable x and y are proportional. Ue the value to find the contant of proportionality. Then write an equation that relate x and y. Write any fraction in implet form. When $y=20$ , $x=12$
Answers
The constant of proportionally with the equation
\($k = \frac{y}{x}$\) with \($y = \frac{5}{3}x$\)
Proportional constant and equationThe constant of proportionality, also known as the coefficient of proportionality, can be found by using the equation:
\($k = \frac{y}{x}$\)
Plugging in the given values of x and y:
\($k = \frac{20}{12}$\)
Which can be simplified to:
\($k = \frac{5}{3}$\)
The equation that relates x and y is:
\($y = kx$\)
Using the equation \($y = kx$\) to find the constant of proportionality, also known as the coefficient of proportionality, and then substituting that value into the equation to relate x and y is one way to solve the problem.
It is the most common way to express a proportionality between two variables and it is the basic form of all proportional relationships.
So, substituting the value of k found earlier:
\($y = \frac{5}{3}x$\)
Learn more about Proportional constant and equation here:
https://brainly.com/question/29126727
#SPJ4
If the variance of a data set is 16, the value of its standard deviation is
a. 4
b. 8
c. 32
d. 256
Answers
The standard deviation is the square root of the variance, so in this case, if the variance of the data set is 16, then the standard deviation would be the square root of 16 which is 4.
The variance is a measure of how spread out the data is from the mean, while the standard deviation tells us how much the data deviates from the mean on average. A larger variance or standard deviation indicates that the data points are more spread out and less consistent, while a smaller variance or standard deviation suggests that the data is more tightly clustered around the mean. Knowing the variance and standard deviation of a data set can be useful for understanding the overall distribution and variability of the data, and can help in making informed decisions or drawing conclusions based on the data.
To know more about standard deviations, visit:
https://brainly.com/question/23907081
#SPJ11
The vector
A
has a magitude of A=12 m and a direction equal to the standard angle, θ
A
=43
0
. What is −
A
? a. Magnitude =9.0 m; Direction = the standard angle 137
∘
. b. Magnitude =12 m; Direction = the standard angle 43
0
. c. Magnitude =−12 m; Direction = the standard angle 223
0
. d. Magnitude =12 m; Direction = the standard angle 223
∘
. e. Magnitude =9.0 m; Direction = the standard angle 223
∘
.
Answers
The vector -A has a magnitude of 12 m and a direction of 223° in standard angle notation.Therefore, the correct answer is: c. Magnitude = -12 m and Direction = 223°.
To find the vector -A, we need to reverse the direction of vector A while keeping its magnitude unchanged. Given that the magnitude of vector A is A = 12 m and its direction is θ_A = 43°, we can reverse the direction by adding 180° to θ_A. Adding 180° to 43° gives us θ_A' = 223°.
So, the vector -A has the same magnitude of 12 m but a direction of 223°. The correct answer is option c: Magnitude = -12 m; Direction = the standard angle 223°.
It's important to note that reversing the direction of a vector changes its sign but not its magnitude. In this case, the magnitude of A remains the same at 12 m, but the negative sign indicates the opposite direction.
Therefore, option a, b, d, and e are incorrect as they either do not have the correct magnitude or do not have the reversed direction. Option c is the only one that satisfies both conditions.
Learn more about magnitude here: https://brainly.com/question/31616548
#SPJ11
6a) find the value of x in the following proportions. a) 3:5=12:x b) 4:3=20:x c) 5:6=x:12 d) 7:2=x:6
Answers
Answer:
A. x = 20
B.x = 15
C. x = 10
D. x = 21
Step-by-step explanation:
In pic they are in order
(Credit: Symbolab)
(Hope this helps can I pls have brainlist (crown)☺️)




LOOKS EASY !! NO FILES/LINK THX
Answers
A washer and dryer cost $1065. The cost of the washer is two times the cost of the dryer. Find the cost of each item.
Answers
Answer:
$250
Step-by-step explanation:
The dryer costs x dollars
The washer costs 3x dollars
3x + x = 1000
4x = 1000
x = 250
The dryer is $250
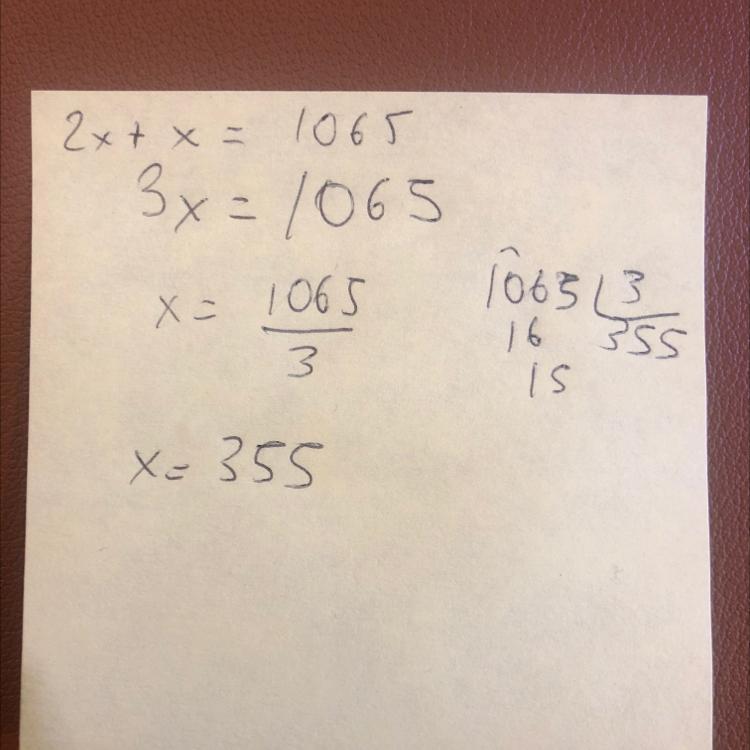
in 2004, a school's population was 1022 . by 2008 the population had grown to 1766 . assume the population is changing linearly. a . how much did the population grow between the year 2004 and 2008? 744 students b . how long did it take for the population to grow from 1022 students to 1766 ? 4 years c . what is the average population growth per year? students per year d . what was the population in the year 2000? students
Answers
The correct answers about school's population and year are - a. 744, b. 4 years, c. 186 and d. 1208.
The population growth between 2004 and 2008 = population in 2008 - population in 2004
Population growth = 1766 - 1022
Population growth = 744
Time taken for population to reach = final population year - initial population year
Time taken = 2008 - 2004
Time taken = 4 years
Average population growth per year = (final - initial year)/(final - initial population)
Average population growth per year = (1766 - 1022)/(2008 - 2004)
Average population growth per year = 744/4
Average population growth per year = 186
(Year 2004 - year 2001) × Average = (Population in year 2004 - population in year 2000)
3 × 186 = 1766 - Population in year 2000
558 = 1766 - Population in year 2000
Population in year 2000 = 1766 - 558
Population in year 2000 = 1208
Thus, the answers are 744, 4 years, 186 and 1208.
Learn more about population-
https://brainly.com/question/130657
#SPJ4
a motorboat moves across a lake at a constant speed. when it begins it from the shore. after 9 minitues it is 14 km from the shore. which function decribes the motorboat distance from the shore?
a. y= 4x + 50
b. y= -4x + 50
c. y= 9x + 50
d. y= -9x + 50
Answers
Answer:
Answer:
The function describes the motorboat's distance from the shore
Step-by-step explanation:
A motorboat moves across a lake as a constant speed. when it begins, it is 50 km from the shore
After 9 minutes, it is 14 km from the shore.
So, rate of change =
Negative sign shows that there is decrease in distance per minute
The rate of change of distance is 4 km / minutes
General equation : y = mx+c
Where m is the slope and c is the constant
Substitute the values in the equation :
y=-4x+50
Where y is the final distance and x is the minutes
So, Option C is true
Hence The function describes the motorboat's distance from the shore
Step-by-step explanation:
A single gram of a certain metallic substance has 0.52 gram of copper and 0.26 gram of zinc. The remaining portion of the substance is nickel. Ben estimated that 0.2 gram of nickel is in 1 gram of the substance. He used this to estimate the amount of nickel in 35 grams of the substance. Find the result of Ben’s estimate strategy. Then find the exact amount of nickel in 35 grams of the substance.
Answers
In one gram of substance 0.22 grams of nickel is present. Then the amount of nickel in the 35 grams of the substance is 7.7 grams.
What are ratio and proportion?A ratio is an ordered couple of numbers a and b, written as a/b where b can not equal 0. A proportion is an equation in which two ratios are set equal to each other.
A single gram of a certain metallic substance has 0.52 grams of copper and 0.26 grams of zinc.
The remaining portion of the substance is nickel.
Let the gram of nickel be x. Then we have
\(\sf x + 0.52 + 0.26 = 1\)
\(\sf x = 0.22\)
0.22 grams of nickel.
Ben estimated that 0.2 gram of nickel is in 1 gram of the substance.
He used this to estimate the amount of nickel in 35 grams of the substance.
Then we have
\(\sf \rightarrow35 \times 0.2 = 7\)
We know that in 1 gram the amount of nickel is 0.22 gram. Then we have
\(\sf \rightarrow 35 \times 0.22 = 7.7\)
The amount of nickel in the 35 grams of the substance is 7.7 grams.
More about the ratio and the proportion link is given below.
brainly.com/question/14335762
Joey is building a frame for a sandbox. The sandbox is going to be a quadrilateral that has the lengths shown. A rectangle is shown. The length of the top and bottom sides are 8 feet, and the length of the left and right sides are 12 feet. A diagonal that is 14 feet long is drawn from the bottom one corner of the rectangle to the other corner of the rectangle. Points X and C are opposite to the diagonal. If the diagonal of the sandbox measures 14 feet, which best describes the shape of the sandbox? a rectangle, because angle C is a right angle a rectangle, because angle C and angle X are congruent a quadrilateral, because angle C and angle X are acute a quadrilateral, because angle C and angle X are obtuse
Answers
Answer:
C) a quadrilateral, because angle C and angle X are acute
Step-by-step explanation:
It is a quadrilateral because angle C and angle X are acute angles and not right angles option third is correct.
What is quadrilateral?It is defined as the four-sided polygon in geometry having four edges and four corners. It has two pairs of congruent sides and one pair of opposite congruent angles.
From the Pythagoras theorem:
\(14^2=12^2+8^2\)
196 ≠ 208
The angles C and X are not right angles since angles C and X are congruent and acute angles.
Thus, it is a quadrilateral because angle C and angle X are acute angles and not right angles option third is correct.
Learn more about the quadrilateral here:
brainly.com/question/6321910
#SPJ2
Need help with this question

Answers
the department of transportation of a city has calculated that on average there are 18 accidents per day. what is the average number of accidents an example of?
Answers
The average number of accidents per day (18 accidents) is an example of a statistical measure of central tendency, specifically the mean. It represents the sum of all the observations (the number of accidents) divided by the total number of observations (the number of days). It is a single value that attempts to describe the entire set of observations.
Mean Of Accidents per DayThe average number of accidents per day can be used to calculate various things. For example, it can be used to:
Estimate the total number of accidents over a certain period of time by multiplying the average number of accidents per day by the number of days in that period.Compare the number of accidents in one city to the number of accidents in another city by comparing their respective averages.Make predictions about future accident rates by assuming that the average number of accidents per day will stay the same.Compare the accident rate of a certain period of time to a previous period of time by calculating the average number of accidents per day for both periods and comparing them.It's important to keep in mind that the mean is just one measure of central tendency, and other measures such as the median or mode may provide a better representation of the data in certain situations.
Learn more about Mean Of Accidents per Day here:
https://brainly.com/question/15286614
#SPJ4
2(x+y)=3(y-1)
If y=5 in the equation above, what is x?
Answers
Answer:
X=1
Step-by-step explanation:
2(X+5)=3(5-1)
2x+10=3*4
2x=12-10
2x=2
X=2÷2
X=1
the covariance and the correlation coefficient between two variables should always have the same sign.True/False
Answers
The covariance and the correlation coefficient between two variables should always have the same sign is False.
The covariance and the correlation coefficient between two variables can have different signs. The covariance is a measure of the direction and strength of the linear relationship between two variables. It can be positive, indicating a positive relationship where both variables move in the same direction, or negative, indicating an inverse relationship where the variables move in opposite directions.
On the other hand, the correlation coefficient is a standardized measure of the linear relationship between two variables, ranging from -1 to 1. It can also be positive or negative, depending on the direction of the relationship, but its magnitude is always between 0 and 1, indicating the strength of the relationship.
To know more about covariance refer here:
https://brainly.com/question/28135424
#SPJ11