What is arcsin(cos3/5)
Giving brainliest please help
Answers
Answer:
(cos(3°) / 5) = 0.201078184 radians
Step-by-step explanation:
Answer:
\(\frac{5\pi-6 }{10} \)
Step-by-step explanation:
We know -pi/2 < x < pi/2
We also know that a = arcsin(b)
so sinx = cos3/5
We will then be left with (5pi-6)/10 in radians, or 55 degrees
Best of luck
Related Questions
what are the dimensions of a rectangular prism with a surface area of 24cm^2
Answers
Answer: 0.0024 m2
Step-by-step explanation:
The 2 at the end was suppost to be little but i could not make it little
Consider an online support group which tackles opioid addiction patients. This is an example of digital health social network (DHSN). Suppose that there are 2 potential influencers and 40 potential patients. Let ni be the number of influencers who decide to join the network. Let na be the number of patients who decide to join the network. Assume that everyone is very conservative and will only join the network if the willingness-to-pay of joining is higher than or equal to his/her time cost. The time cost of joining the network is $20 and $5 for influencers and patients, respectively. Assume the willingness-to-pay functions described below are expressed in dollar value. Influencers (side 1) are content contributors, their willingness-to-pay function (u') of joining the network is: • If n2 = 0, u' = 0. If n2 > 0, u' = 2*n/n. Patients (side 2), who seek help, have the following willingness-to-pay function (u"): If n = 0, up = 0. If n = 1: u' =10, for n2<=10. • uP =10/(0.1*n2), for n2>10. [Too many participants → congestion!)? If n = 2: u' =10, for nz<=20. • u' =10/(0.05*n2), for n2>20. (a) Given the assumptions set above, if the company just starts this platform (i.e., it starts with 0 participants from both sides), how many participants will join on each side? Explain your answers.
Answers
Given the assumptions set above, the number of participants that will join the network on each side is as follows: two influencers and 17 patients.
Explanation :From the given data, the time cost of joining the network is $20 and $5 for influencers and patients, respectively. Influencers (side 1) are content contributors, their willingness-to-pay function (u') of joining the network is:• If n2 = 0, u' = 0. If n2 > 0, u' = 2*n/n. Patients (side 2), who seek help, have the following willingness-to-pay function (u"):If n = 0, up = 0. If n = 1: u' =10, for n2<=10.• uP =10/(0.1*n2), for n2>10.If n = 2: u' =10, for nz<=20.• u' =10/(0.05*n2), for n2>20.By putting n = 0 in u" equation, we get u" = 0 as there are no patients initially. By putting n = 1 in u" equation, we get u" = 10 as n2 = 0.
Since n2 = 0, putting n = 2 in u" equation, we get u" = 10 as well. Therefore, both the influencers will join as they both have u' > 20 and the maximum number of patients who can join the network are 17. This is because when n = 1, u" = 10 and n2 <= 10. For n = 2, the maximum number of patients who can join the network is 17 as per the equation u" = 10/(0.1*n2). Putting n2 = 17 in the equation, we get u" = 5.88 which is less than their time cost of joining the network.
Know more about influencers here:
https://brainly.com/question/14704970
#SPJ11
Which pair of angles are complementary but not adjacent?
O 1 and 25
O 1and 3
O 4 and 1
O 4 and 5
Answers
How to graph y= 3/4x- 1/2
Answers
The answer of the given question on how to graph y=3/4x-1/2 the following steps are given below.
What is y-intercept?The y-intercept is point where graph crosses y-axis. In other words, it is the point where x = 0 and the value of y is some number.
In the equation of a straight line in the form y = mx + b (where m is the slope of the line and b is the y-intercept), the y-intercept is the constant term (b) that appears without any x-variable.
For example, in the equation y = 2x + 3, the y-intercept is 3, since it is the value of y when x is zero. Similarly, in the equation y = -1/2x + 4, the y-intercept is 4, since it is the value of y when x is zero.
The y-intercept is an important property of a straight line, as it helps us to identify the starting point of the line and gives us an idea of the position of the line on the y-axis.
To graph the equation y = (3/4)x - (1/2), we can follow these steps:
Choose a range of x-values to plot. For example, we can choose x-values from -2 to 2.
Substitute each x-value into equation to find corresponding y-value. For example,
when x = -2, we have:
y = (3/4)(-2) - (1/2)
= -3/2
So the first point we can plot is (-2, -3/2).
Repeat step 2 for several more x-values to find additional points. For example, when x = -1, we have:
y = (3/4)(-1) - (1/2)
= -5/4
So we can plot the point (-1, -5/4).
Similarly, when x = 0, we have:
y = (3/4)(0) - (1/2)
= -1/2
So we can plot the point (0, -1/2).
Continuing this process for a few more values of x, we can get more points to plot.
Plot the points on the coordinate plane and connect them with a straight line.
Note that since the coefficient of x is positive (3/4), the line has a positive slope. Additionally, the y-intercept of the line is -1/2. Therefore, we can start by plotting the point (0, -1/2), which is where the line crosses the y-axis.
To know more about Equation visit:
https://brainly.com/question/9312365
#SPJ1
What value of n makes the equation true?
2/3n = -12
n=
Answers
Answer:
-18
Step-by-step explanation:
\(\frac{2}{3}n=-12 \\ \\ \frac{3}{2} \cdot \frac{2}{3}n=\frac{3}{2}(-12) \\ \\ n=-18\)
Find the area. Simplify your answer.
x+1
2x

Answers
Answer:
\(A = x^{2} + x\)
Step-by-step explanation:
Area of a triangle = bh/2
Your base is 2x and the height is x + 1
So, A = (2x)(x + 1)/2
A = \(x^{2} + x\)
Factor the expression
36x + 27 using the GCF.
Answers
Answer:
9(4x+3) :)
Step-by-step explanation:
Answer:
Step-by-step explanation:
the first step in factorising is to look for any common factors.
27
and
36
are both multiples of
3
and
9
.
We use
9
because it is the highest common factor:
Divide
9
out of each term:
27+36x=9(3+4x)
The reverse process would be to use the distributive law to multiply each term in the bracket by
9
.
This will give us the original expression:
9(3+4x)=27+36x
Find the value of ∠R

Answers
Answer:
∠ R = 30°
Step-by-step explanation:
The secant- secant angle R is half the difference of its intercepted arcs, so
∠ R = \(\frac{1}{2}\) (103 - 43)° = \(\frac{1}{2}\) × 60° = 30°
Figure below shows a rotating shaft made of AISI 1095 Normalized steel supported by two bearings with reaction forces R₁ and R₂. Location A and Location Care where bearings are installed and there is a stress reducing groove at location B with 2.5 mm depth. The surface of part AB is ground while the grooved is machined. The shaft is subjected to two bending forces of 5 kN and 10 kN as shown in the figure, and a constant torque T = 300 Nm (not shown in the figure). Check if this shaft can last for infinite-life.
Answers
To determine if the rotating shaft made of AISI 1095 Normalized steel can last for infinite life, we need to analyze the stress levels and fatigue strength of the shaft under the given loading conditions. The shaft is subjected to bending forces and a constant torque.
We need to assess whether the stress levels at critical locations, such as the stress reducing groove, are within the allowable limits and if the fatigue strength of the material is sufficient to withstand the cyclic loading.
To evaluate the infinite life of the shaft, we need to consider the fatigue properties of AISI 1095 Normalized steel. This involves determining the maximum stresses induced in the shaft due to the bending forces and torque. By analyzing the geometry and applying the principles of mechanics, we can calculate the stresses at critical locations.
The stress reducing groove at location B introduces a stress concentration factor, which needs to be taken into account when assessing the stress levels. The depth of the groove and the material properties of AISI 1095 Normalized steel influence the stress concentration factor.
To assess the fatigue strength of the material, we need to compare the maximum stresses with the endurance limit or fatigue strength of AISI 1095 Normalized steel. If the maximum stresses are below the endurance limit, the shaft can be considered to have an infinite life.
By evaluating the stress levels and comparing them with the fatigue strength of AISI 1095 Normalized steel, we can determine if the rotating shaft can withstand the given loading conditions without experiencing fatigue failure. If the stress levels are within the allowable limits and the fatigue strength is sufficient, the shaft can be expected to last for an infinite life.
Learn more about torque here : brainly.com/question/30338175
#SPJ11
A(n) ______________________________ is formed by one side of the triangle and the extension of an adjacent side.
Answers
A triangle is a three-sided polygon that consists of three sides and three angles. An extension of a side of a triangle is a line segment that is drawn from one of the endpoints of the side that extends beyond the side.
If we extend one side of the triangle and draw a line that passes through one of the adjacent vertices, the resulting shape is called a triangle's exterior angle. This exterior angle is formed by one side of the triangle and the extension of an adjacent side.
In other words, an exterior angle of a triangle is an angle that is formed by one side of a triangle and the extension of an adjacent side of the triangle.
To know more about polygon. here
https://brainly.com/question/1592456
#SPJ4
Jacque is using a soup can for a school project and wants to paint it. If the can is 11 cm tall and has a diameter of 9 cm, at least how many square centimeters of paint is needed? Approximate using π = 3.14.
374.45 cm2
139.50 cm2
699.44 cm2
438.03 cm2
Answers
The approximate amount of paint needed = 438.03 cm²
The correct answer is an option (D)
We know that the formula for the surface area of the cylinder is :
A = (2 × π × r × h) + (2 × π × r²)
Here, the diameter of the can is 9 sm
So, the radius of the can would be,
r = d/2
r = 9/2
r = 4.5 cm
And the height of the can is h = 11 cm
Since the can is cylindrical, we use above formula of surface area of the cylinder to find the amount of paint needed.
Using above formula,
A = (2 × π × r × h) + (2 × π × r²)
A = (2 × π × (4.5) × (11)) + (2 × π × (4.5)²)
A = 311.02 + 127.01
A = 438.03 cm²
Therefore, the correct answer is an option (D)
Learn more about the surface area of the cylinder here:
brainly.com/question/31178158
#SPJ1
Force f acts between a pair of charges, q1 and q2, separated by a distance d. for each of the statements, use the drop-down menus to express the new force in terms of f. q1 is halved, q2 is doubled, but the distance between the charges remains d. q1 and q2 are unchanged. the distance between the charges is doubled to 2d. q1 is doubled and q2 is tripled. the distance between the charges remains d.
Answers
The initial force between the two charges is given by:
\(F=k\frac{q_{1} q_{2} }{d^2}\)
where k is Coulomb's constant, q1 and q2 are the two charges, and d is their separation. Let's analyze now the other situations:
1. F
In this case, q1 is halved, q2 is doubled, but the distance between the charges remains d.
So, we have:
q'₁=q₁/2
q'₂=2q₂
d'=d
So, the new force is:
\(F'=k\frac{q'_{1}q'_{2} }{d^2} \\\\F'=k\frac{(\frac{q_{1} }{2})(\frac{q_{2} }{2}) }{d^2} \\\\F'=k\frac{q_{1}q_{2} }{d^2} =F\)
So the force has not changed.
2. F/4
In this case, q1 and q2 are unchanged. The distance between the charges is doubled to 2d.
So, we have:
q'₁=q₁
q'₂=q₂
d'=2d
So, the new force is:
\(\\F'=k\frac{q'_{1} q'_{2} }{d^2} \\\\F'=k\frac{q_{1}q_{2} }{2d^2} \\\\F'=\frac{1}{4} k\frac{q_{1}q_{2} }{d^2} \\\\F'=\frac{F}{4}\)
So the force has decreased by a factor of 4.
3. 6F
In this case, q1 is doubled and q2 is tripled. The distance between the charges remains d.
So, we have:
q'₁=2q₁
q'₂=3q₂
d'=d
So, the new force is:
\(F'=k\frac{q'_{1} q'_{2} }{d^2} \\\\F'=k\frac{2q_{1}3q_{2} }{d^2}\\ \\F'=6k\frac{q_{1}q_{2} }{d^2} =6F\)
So the force has increased by a factor of 6.
To know more about the distance between charges:
https://brainly.com/question/12288272
#SPJ4
Answer:
1. F
2. F/4
3. 6F
HELP ASAP PLEASE! THANKS!
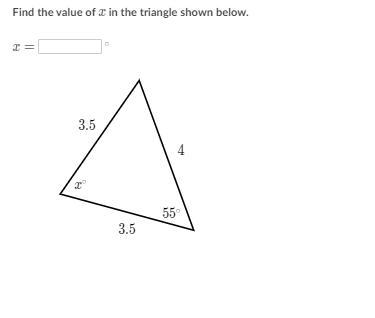
Answers
Answer:
m∠x = 70°
Step-by-step explanation:
Since both 3.5 sides are congruent, then we have an isosceles triangle. That means the other unknown angle measure is also 55°. Since all angles of a triangle add up to 180°,
x + 55(2) = 180
x + 110 = 180
x = 70°
Three identical squares are placed side by side to form a rectangle with a perimeter of 104 inches. What is the area, in square inches, of each square?
Answers
Answer:
13 inches
Step-by-step explanation:
I have done a Little draw because I don't know how i can explain you this exuse me

Ana is going to a craft fair where she'll sell her handmade scarfs. She has six scarf designs, and she's made 15 of each. She's paid $128 for the booth, and each scarf costs $9.80 to make. How much should she charge for each scarf if she wants to break even after selling a third of her scarves?
Answers
Answer:
$33.6667
Step-by-step explanation:
Given the following :
Number of Scarf designs = 6
Number of each made = 15
Total scarfs = (15 * 6) = 90
Cost:
Booth = $128
Production cost per scarf = $9.80
Total production cost = $9.80 * 90 = $882
Total cost = $128 + $882 = $1010
Break even = profit - loss = 0
One third of scarves = 1/3 * 90 = 30
This means he must cover for the total cost of $1010 after selling 30 scarves
Hence price per scarf will be :
$1010 / 30
= $33.6667
A triangle has sides with lengths of 40 yards, 75 yards, and 85 yards. Is it a right triangle?
Answers
Answer:
Yes
Step-by-step explanation:
To check, the squared values of the two smaller lengths must equal the squared value of the biggest length (Pythagorean Theorem)
40² + 75² = 85²
1600 + 5625 = or ≠ 7225
7225 = 7225
It is equivalent so it is correct.
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
Larger values of r^2
imply that the observations are more closely grouped about the:
a. average value of the independent variables.
b. average value of the dependent variable.
c. least-squares line.
d. origin.
e. None of the above answers is correct.
Answers
Larger the value of r² (R²) imply that the observations are more closely grouped about the least squares line (regression line) option C.
The dependent variables on the y-axis and the independent variables on the x-axis are shown as a linear connection by a regression line. By examining the data pattern the variables' effects have created, the correlation is established.
As the (R2) is large therefore, the model is a good fit or bounded close to regression line least squares line (regression line).
In a regression graph, the regression line that is closest to the data points is shown. By changing the value of x in the regression equation, this statistical tool helps study how a dependant variable y behaves when the independent variable x changes.
Learn more about Regression Line:
https://brainly.com/question/17004137
#SPJ4
Complete question:
Larger values of r2 (R2) imply that the observations are more closely grouped about the
Group of answer choices:
average value of the dependent variableoriginleast squares line (regression line)average value of the independent variablesJames started an apple orchard with the trees he already had and then planted 25 more. Now his orchard contains 44 trees. How many trees did James start out with?
Answers
use arc length formula to find the length of the curve y=sqrt(2-x^2) (0 < x < 1)
Check your answer noting the curve is part of a circle.
Answers
The length of the curve y=\(\sqrt{(2-x^2)}\) (0 < x < 1) by using arc length formula is L = 4 - \(4\sqrt{2}\).
To find the length of the curve given by the equation \(y = \sqrt{(2 - x^2)}\) for 0 < x < 1, we can use the arc length formula. The formula for arc length is:
L = ∫[a, b] \(\sqrt{(1 + (dy/dx)^2)}\) dx
where a and b are the limits of integration, and dy/dx represents the derivative of y with respect to x.
First, let's find dy/dx. Differentiating \(y = \sqrt{(2 - x^2) }\)with respect to x, we get:
dy/dx = d/dx \(\sqrt{(2 - x^2)}\)
To differentiate this, we can use the chain rule:
\(dy/dx = (-1/2)(2 - x^2)^{(-1/2)(-2x)}\)
= \(x / \sqrt{(2 - x^2)}\)
Now we can substitute this into the arc length formula:
L = ∫[0, 1] \(\sqrt{(1 + (dy/dx)^2) }\)dx
= ∫[0, 1] \(\sqrt{(1 + (x / \sqrt{(2 - x^2))^2}\)dx
Simplifying the expression inside the square root:
L = ∫[0, 1] \(\sqrt{(1 + x^2 / (2 - x^2))}\) dx
= ∫[0, 1] \(\sqrt{((2 - x^2 + x^2) / (2 - x^2))}\) dx
= ∫[0, 1] \(\sqrt{(2 / (2 - x^2))}\) dx
Now we can evaluate this integral to find the length of the curve.
To evaluate the integral L = ∫[0, 1] \(\sqrt{(1 + x^2 / (2 - x^2))}\) dx, we can simplify the expression inside the square root and then proceed with the integration.
Let's start by simplifying:
L = ∫[0, 1] \(\sqrt{((2 - x^2 + x^2) / (2 - x^2))}\) dx
= ∫[0, 1] \(\sqrt{(2 / (2 - x^2))}\) dx
Now, let's make a substitution to simplify the integrand. We'll substitute u = 2 - x^2, which implies du = -2x dx. We can solve for x in terms of u:
u = \(2 - x^2\)
\(x^2\) = 2 - u
x = \(\sqrt{(2 - u)}\)
Now, we need to find the new limits of integration when x = 0 and x = 1:
When x = 0:
u = 2 - \(0^2\) = 2
When x = 1:
u = 2 - \(1^2\) = 1
The integral in terms of u becomes:
L = ∫[2, 1] √(2/u) du
To simplify this further, we can pull out the constant 2 from the square root:
L = 2∫[2, 1] \(\sqrt{(1/u)}\) du
= 2∫[2, 1] \(u^{(-1/2)}\) du
Now, we can integrate using the power rule:
L = 2[2\(u^{(1/2)}\)]∣[2, 1]
= 2[\(2(1)^{(1/2)} - 2(2)^{(1/2)\)]
= 2[2 - 2\(\sqrt{2}\)]
Finally, we can simplify:
L = 4 - 4\(\sqrt{2}\)
Therefore, the length of the curve y = \(\sqrt{(2 - x^2)}\) for 0 < x < 1 is L = 4 - \(4\sqrt{2}\).
Learn more about Arc Length at
brainly.com/question/31762064
#SPJ4
help!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!


Answers
The distance that Evan has left to hike is 13/30 mile.
How to calculate the distance left?From the information, Eva is hiking a real that has a length of 5/6 miles.
He has also hiked 2/5 miles. Therefore, in this situation, the distance that he has left will gotten by subtracting the fractions.
This will be:.
Distance left = Total distance - Distance hiked
Distance left = 5/6 - 2/5
= 25/30 - 12/30
= 13/30
The distance is 13/30 miles.
Learn more about fractions on:
brainly.com/question/17220365
#SPJ1
Double Points! (i have no clue how to do this)
Find the value of the variables in the figure.

Answers
Answer:
x=12 and y=31
Step-by-step explanation:
First, ( 5x - 7 ) and ( 3x + 17 ) are alternate interior angles, which means they are congruent, or equal:
5x - 7 = 3x + 17
Add 7 to each side:
5x = 3x + 24
Subtract 3x from both sides:
2x = 24
Divide each side by 2:
x = 12
Now we can see that ( 5x - 7 ) and ( 4y + 3 ) are supplementary angles, which means they will add up to 180 degrees:
5x - 7 + 4y + 3 = 180
Substitute 12 in for x to solve for y:
5 ( 12 ) - 7 + 4y + 3 = 180
60 - 7 + 4y + 3 = 180
combine like terms:
( 60 + ( -7 ) + 3 ) + 4y = 180
56 + 4y = 180
Subtract 56 from each side:
4y = 124
Divide each side by 4:
y = 31
12 = -4(-6x - 3)
x=
i made this 19 points please help
Answers
Answer:
0
Step-by-step explanation:
-4 times -6x is 24x and-4 x -3 = 12
isolating 24x on the right side we subtract twelve on the right and on the left to get 24x=0 and 24 divided by zero is 0
Answer:
I think the answer is x=0
Step-by-step explanation:
Khan Academy
layer 1
layer 2
layer 3
surface
layer 4
layer 1 and layer 4
layer 2 and layer 6
layer 3 and layer 5
layer 5
layer 6
surface
Which two layers are approximately the same age?
Answers
Layer 1 and Layer 4 are approximately the same age.
The geological structure of the earth's crust can be analyzed by studying the layers of sedimentary rocks. These layers represent various geological periods in the history of the Earth and provide information on the events that have occurred throughout time.
The Khan Academy is an online platform that offers various courses and lessons on different subjects, including geology. The different layers of the earth's crust are named and classified according to their age, composition, and position in the crust. The layers of the earth's crust are as follows:
Layer 1: The surface layer or the soil. It is the layer that contains the organic matter that supports plant growth.
Layer 2: The subsoil, which is composed of partially decomposed organic matter and clay.
Layer 3: The layer of weathered rock. It is the layer that has been altered by the action of water and wind.
Layer 4: The solid bedrock that is composed of igneous, metamorphic or sedimentary rocks. This layer is considered to be the oldest layer of the earth's crust.
Layer 5: The asthenosphere, which is a semi-solid layer of the upper mantle.
Layer 6: The mantle, which is the thickest layer of the earth's crust. The two layers that are approximately the same age are layer 1 and layer 4. Layer 1, which is the surface layer or the soil, is relatively young and is formed by the accumulation of organic matter.
On the other hand, layer 4 is the solid bedrock that is composed of igneous, metamorphic or sedimentary rocks. This layer is considered to be the oldest layer of the earth's crust.
Therefore, layer 1 and layer 4 are approximately the same age.
For more questions on Layer .
https://brainly.com/question/31298922
#SPJ8
A particle which moves with curvilinear motion has coordinates in millimeters which vary with the time t in seconds according to x= 1.3t
2
−6.6t and y=2.8t
2
−t
3
/4.0. Determine the magnitudes of the velocity v and acceleration a and the angles which these vectors make with the x-axis when t=4.1 s. Answers: When t=4.1 s
v=
a=
mm/s,
mm/s
2
,
θ
x
=
θ
x
=
eTextbook and Media
Answers
To find the magnitudes of the velocity (v) and acceleration (a) and the angles they make with the x-axis at t = 4.1 s, we need to differentiate the given equations for x and y with respect to time (t).
Given:
x = 1.3t^2 - 6.6t
y = 2.8t^2 - (t^3)/4.0
Velocity (v):
The velocity is the rate of change of position with respect to time. It can be calculated by taking the derivatives of x and y with respect to t:
vx = dx/dt = d/dt(1.3t^2 - 6.6t)
vy = dy/dt = d/dt(2.8t^2 - (t^3)/4.0)
Calculate vx and vy by differentiating the expressions:
vx = 2.6t - 6.6
vy = 5.6t - (3t^2)/4.0
At t = 4.1 s, substitute t = 4.1 into vx and vy to find the components of the velocity vector at that time.
Acceleration (a):
The acceleration is the rate of change of velocity with respect to time. We can calculate it by taking the derivatives of vx and vy with respect to t:
ax = d(vx)/dt = d/dt(2.6t - 6.6)
ay = d(vy)/dt = d/dt(5.6t - (3t^2)/4.0)
Calculate ax and ay by differentiating the expressions:
ax = 2.6
ay = 5.6 - (3t)/2.0
Again, substitute t = 4.1 s into ax and ay to find the components of the acceleration vector at that time.
Angles with the x-axis (θx):
To find the angles that the velocity and acceleration vectors make with the x-axis, we can use the inverse tangent function:
θx = arctan(vy / vx)
Calculate θx using the values of vx and vy at t = 4.1 s.
Substitute the values of v, a, and θx into the answers to complete the solution.
To learn more about acceleration : brainly.com/question/2303856
#SPJ11
PQ= RQ and PS= RS a=?

Answers
The measure of angle a is 15 degrees and this can be determined by using the properties of the isosceles triangle.
What are interior angles?In geometry, interior angles are formed in two ways. One is inside a polygon, and the other is when parallel lines cut by a transversal. Angles are categorized into different types based on their measurements.
Given:
The length of the segment PQ is equal to the length of the segment RQ.The length of the segment PS is equal to the length of the segment RS.The following steps can be used in order to determine the measure of angle a:
Step 1 - According to the given data, it can be concluded that triangle PQR and triangle PSR are isosceles triangles.
Step 2 - Apply the sum of interior angle property on triangle PQR.
\(\angle\text{Q}+\angle\text{P}+\angle\text{R}=180\)
\(\angle\text{Q}+2\angle\text{R}=180\)
\(2\angle\text{R}=180-60\)
\(\angle\text{R}=60^\circ\)
Step 3 - Now, apply the sum of interior angle property on triangle PSR.
\(\angle\text{P}+\angle\text{S}+\angle\text{R}=180\)
\(\angle\text{S}+2\angle\text{R}=180\)
\(2\angle\text{R}=180-90\)
\(\angle\text{R}=45^\circ\)
Step 4 - Now, the measure of angle a is calculated as:
\(\angle\text{a}=60-45\)
\(\angle\text{a}=15\)
The measure of angle a is 15 degrees.
For more information on interior angles, refer to the link given below:
https://brainly.com/question/28795639
Natalie needs to compare the number of employees by job title for the last five years. Which of the following charts should Natalie use?
Answers: A. Pie chart
B.Clustered column chart
C.Histogram
D.Scatter chart
Answers
Natalie should use Clustered Column Chart.
What is a Clustered Column Chart?
A clustered column chart is a vertical representation that shows data in groups (columns) that are connected to one another. Each column's data is separated into categories according to an attribute like year, age, sex, or race.For the purpose of comparing various variables, many bars are clustered in the same class in a clustered-column (bar) chart which is a specific kind of column (bar) chart. Hence, (B.) Clustered Column Chart is the correct option.
To learn more about clustered column chart from the given link
https://brainly.com/question/13871272
#SPJ4
What is the slope of a line that is perpendicular to the line shown on the graph?
–4
4
Answers
Answer:
its 4
Step-by-step explanation:
got a 100 on the test
Answer:
D
Step-by-step explanation:
The Summary sheet is designed to display two key averages from the PivotTable on the Summary sheet. Display the Summary sheet. In cell B2, insert the GETPIVOTDATA function that references cell C4 on the PivotTable in the Sold Out sheet. In cell B3, insert the GETPIVOTDATA function that references cell C9 on the PivotTable in the Sold Out sheet
Answers
A pivot table is a table of grouped values that aggregates the individual items of a more extensive table within one or more discrete categories. This summary might include sums, averages, or other statistics, which the pivot table groups together using a chosen aggregation function applied to the grouped values.
To display the two key averages from the pivot table on the Summary sheet, follow these steps:
1. Open the Summary sheet.
2. In cell B2, insert the GETPIVOTDATA function. This function retrieves data from a pivot table based on specified criteria.
3. The function in cell B2 should reference cell C4 on the Pivot Table in the Sold Out sheet. This means the formula in B2 should be: =GETPIVOTDATA(C4, Sold Out'!$A$1).
- The first argument of the function (C4) specifies the value or field you want to retrieve from the pivot table.
- The second argument ('Sold Out) specifies the location of the pivot table. 'Sold Out' refers to the name of the sheet where the Pivot Table is located, and A is the cell reference of the top-left cell of the pivot table.
4. In cell B3, insert another GETPIVOTDATA function. This time, the function should reference cell C9 on the pivot table in the Sold Out sheet. The formula in B3 should be: =GETPIVOTDATA(C9,'Sold Out'!$A$1).
- Similar to the previous step, the first argument (C9) specifies the value or field you want to retrieve from the pivot table.
- The second argument ('Sold Out'!$A$1) again specifies the location of the PivotTable.
By using the GETPIVOTDATA function with the appropriate cell references, you can display the desired averages from Pivot Table on the Summary sheet.
Learn more about pivot table: brainly.com/question/27813971
#SPJ11
What is the measurement for the exterior angle

Answers
First we find \(\angle ACB\)
\(\angle ACB = 180 - (4x - 100) = 180 - 4x + 100 = 280 - 4x\)
Then we find a equation for all the interior angles
\(180 = \angle ACB + \angle BAC + \angle ABC\\= 280 - 4x + x + 20 + x\\300 - 2x\)
We solve for x
\(180 = 300 - 2x\\180 - 300 = -2x\\-120 = -2x\\2x = 120\\x = 60\\\)
Now we find the exterior angle
\(\angle DCB = 4x - 100 = 4 \cdot 60 - 100 = 240 - 100 = 140\)
Simplify these expressions
a) 2a + 5a
Answers
Answer:
\(\mathsf {7a}\)
Step-by-step explanation:
\(\textsf {Here, both terms contain the variable 'a'.}\\\textsf {Hence, they can be added together once the variable}\\\textsf {is taken as a common factor.}\)
\(\implies \mathsf {2a + 5a}\)
\(\implies \mathsf {a(2 + 5)}\)
\(\implies \mathsf {7a}\)
Answer:
7a
Step-by-step explanation:
To solve this you have combine like terms.
That is, you have to simply add those numbers together.
Let us solve now
2a + 5a
= 7a