what is ordered pair
Answers
Answer:
see explanation
Step-by-step explanation:
An ordered pair is a set of coordinates (x, y )
This can be o point on a graph or the solution to a system of equations or values from a table
Answer: It's a point on a graph (y,x)
Step-by-step explanation:
Related Questions
Please Explain:
For each pair of the following functions, fill in the correct asymptotic notation among Θ, o, and ω in statement f(n) ∈ ⊔(g(n)). Provide a brief justification of your answers
f(n) = n^3 (8 + 2 cos 2n) versus g(n) = n^2 + 2n^3 + 3n
Answers
The asymptotic notation relationship between the functions \(f(n) = n^3 (8 + 2 cos 2n)\) and \(g(n) = n^2 + 2n^3 + 3n\) is f(n) ∈ Θ(g(n)). Therefore, the growth rates of f(n) and g(n) are primarily determined by the cubic terms, and they grow at the same rate within a constant factor.
To determine the asymptotic notation relationship between the functions \(f(n) = n^3 (8 + 2 cos 2n)\) and \(g(n) = n^2 + 2n^3 + 3n\), we need to compare their growth rates as n approaches infinity.
Θ (Theta) Notation: f(n) ∈ Θ(g(n)) means that f(n) grows at the same rate as g(n) within a constant factor. In other words, there exists positive constants c1 and c2 such that c1 * g(n) ≤ f(n) ≤ c2 * g(n) for sufficiently large n.
o (Little-o) Notation: f(n) ∈ o(g(n)) means that f(n) grows strictly slower than g(n). In other words, for any positive constant c, there exists a positive constant n0 such that f(n) < c * g(n) for all n > n0.
ω (Omega) Notation: f(n) ∈ ω(g(n)) means that f(n) grows strictly faster than g(n). In other words, for any positive constant c, there exists a positive constant n0 such that f(n) > c * g(n) for all n > n0.
Now let's analyze the given functions:
\(f(n) = n^3 (8 + 2 cos 2n)\\g(n) = n^2 + 2n^3 + 3n\)
Since both functions have the same dominant term, we can say that f(n) ∈ Θ(g(n)) because they grow at the same rate within a constant factor. The other notations, o and ω, are not applicable here because neither function grows strictly faster nor slower than the other.
To know more about growth rate,
https://brainly.com/question/33562447
#SPJ11
3. What is the equation of a line parallel to y = -4x + 6 that passes through the
point (2, -1)? *
Answers
y = -4x + b
Plug in a point
-1 = -4(2) + b
-1 = -8 + b, b = 7
Solution: y = -4x + 7
ITS AN ANGLE QUESTION PLS HELP

Answers
Answer:
The values of \(f\) and \(g\) are, respectively:
\(f = 6\,cm\), \(g = 8\,cm\)
Step-by-step explanation:
The area of the triangle ADE is:
\(A_{ADE} = 60\,cm^{2}-48\,cm^{2}\)
\(A_{ADE} = 12\,cm^{2}\)
The area of the triangle is defined by the following formula:
\(A_{ADE} = \frac{1}{2}\cdot AD\cdot DE\) (1)
If we know that \(A_{ADE} = 12\,cm^{2}\) and \(DE = 4\,cm\), then the length of the line segment \(AD\) is:
\(AD = \frac{2\cdot A_{ADE}}{DE}\)
\(AD = 6\,cm\)
And the area of the rectangle is:
\(A_{ABCD} = AD\cdot CD\) (2)
If we know that \(A_{ABCD} = 48\,cm^{2}\) and \(AD = 6\,cm\), then the length of the line segment \(CD\) is:
\(CD = \frac{A_{ABCD}}{AD}\)
\(CD = 8\,cm\)
Hence, the values of \(f\) and \(g\) are, respectively:
\(f = 6\,cm\), \(g = 8\,cm\)
If C is the unit circle in the complex plane C, and f(2)= 2², show that (2) dz = 0 using two ways: (a) by a direct multivariable integration by writing = +iy and suitably parametrizing C, and (b) using a relevant theorem. 2
Answers
(a) To show that the integral of f(z) dz over the unit circle C is equal to 0, we can parametrize C as z(t) = e^(it), where t ranges from 0 to 2π. Substituting this parametrization into f(z) = z^2, we get f(z(t)) = (e^(it))^2 = e^(2it). Now, dz = i e^(it) dt. Plugging these values into the integral, we have ∫[C] f(z) dz = ∫[0 to 2π] e^(2it) (i e^(it)) dt = i ∫[0 to 2π] e^(3it) dt. Evaluating this integral gives [e^(3it)/3i] from 0 to 2π. Substituting the limits, we get [e^(6πi)/3i - e^(0i)/3i].
Since e^(6πi) = 1, the expression simplifies to 1/3i - 1/3i = 0. Therefore, the integral of f(z) dz over C is indeed 0.
(b) By using the Cauchy's Integral Theorem, we can show that the integral of f(z) dz over C is 0. The theorem states that if f(z) is analytic inside and on a simple closed curve C, then the integral of f(z) dz over C is 0. In this case, f(z) = z^2, which is an entire function (analytic everywhere). Since C is the unit circle, which is a simple closed curve, we can apply the theorem. Thus, the integral of f(z) dz over C is 0.
Both methods, direct multivariable integration and the application of Cauchy's Integral Theorem, confirm that the integral of f(z) dz over the unit circle C is equal to 0.
To learn more about Integral Theorem - brainly.com/question/30992206
#SPJ11
A car dealership has 98 cars on its lot. Fifty-five of the cars are new. Of the new cars, 36 are domestic cars. There are 15 used foreign cars on the lot. Organize this information in a two-way table. Include the marginal frequencies
Answers
Here is a two-way table that summarizes the information:
The marginal frequencies (totals) are shown in the last row and last column. The dealership has a total of 98 cars on its lot, which is the sum of the new and used cars. There are 55 new cars and 15 used cars, which is the sum of the domestic and foreign cars in each category.
To know more about marginal frequencies refer here:
https://brainly.com/question/31189964
#SPJ11

33 +4 = 52 – 10
This equation can be simplified by combining like terms to become 8.2 + 4 = -10.
If "False", explain why
True
False

Answers
Solve these problems and give the answer with the correct number of significant figures: (4.307×10^4)×(6.2×10^−3)= 26.127+3.9+0.0324=
Answers
Let's solve the problems and provide the answers with the correct number of significant figures:
(4.307 × 10^4) × (6.2 × 10^-3)
Multiplying the numbers:
(4.307 × 6.2) × (10^4 × 10^-3) = 26.6974 × 10^1
Since the result is in scientific notation, we multiply the decimal part by the power of 10:
26.6974 × 10^1 = 266.974
To express the answer with the correct number of significant figures, we consider the least number of significant figures in the original values, which is three significant figures in this case.
Therefore, the answer is 267 with three significant figures.
26.127 + 3.9 + 0.0324
Adding the numbers:
26.127 + 3.9 + 0.0324 = 30.0594
To express the answer with the correct number of significant figures, we consider the least number of decimal places in the original values, which is one decimal place in this case.
Therefore, the answer is 30.1 with one decimal place.
To learn more about notation visit;
https://brainly.com/question/29132451
#SPJ11
If $10,000 is invested at an interest rate of 4% per year, compounded semiannually find the value of the investment after the given number of years. (Round your answers to the nearest cent.) (a) 6 years (b) 12 years (c) 18 years
Answers
The value of the investment after a certain number of years can be calculated using the compound interest formula:
A = P(1 + r/n)^(nt),
where A is the final amount, P is the principal amount (initial investment), r is the interest rate, n is the number of times interest is compounded per year, and t is the number of years.
For part (a), after 6 years, the investment would grow to A = $10,000(1 + 0.04/2)^(2*6) = $12,167.88.
For part (b), after 12 years, the investment would grow to A = $10,000(1 + 0.04/2)^(2*12) = $14,851.39.
For part (c), after 18 years, the investment would grow to A = $10,000(1 + 0.04/2)^(2*18) = $18,061.13.
In these calculations, the interest rate of 4% per year is divided by 2 because interest is compounded semiannually. The exponent nt represents the total number of compounding periods over the given number of years. By substituting the values into the formula, we can find the value of the investment after each specified time period.
To learn more about compound interest formula click here: brainly.com/question/30287096
#SPJ11
Is the first side “SW=XW” or “ST=XU”?

Answers
Answer:
SW =XW and ST=XU and UW=TW
Step-by-step explanation:
All are true and correct since the two triangles are congruent
Angle S=X are congruent
Sides UW=WT are congruent
Use the solution method from this example to find a basis for the given subspace. S = span {[1 -1 0 2], [3 -5 4 8], [0 1 -2 -1]} Give the dimension of the basis. v
Answers
Answer:
Step-by-step explanation:
The dimension of the basis is {[1 0 0 2], [-1 1 0 0]}.
To find a basis for the subspace S = span {[1 -1 0 2], [3 -5 4 8], [0 1 -2 -1]}, we can use the same method as in the example. First, we put the vectors in a matrix and row-reduce it:
[1 -1 0 2]
[3 -5 4 8]
[0 1 -2 -1]
R2 - 3R1 -> R2
R3 -> R3 + 2R1
[1 -1 0 2]
[0 -2 4 2]
[0 1 -2 -1]
-1/2R2 -> R2
[1 -1 0 2]
[0 1 -2 -1]
[0 1 -2 -1]
R3 - R2 -> R3
[1 -1 0 2]
[0 1 -2 -1]
[0 0 0 0]
We can see that the last row is all zeros, so we have only two pivots and one free variable. This means that the dimension of the subspace S is 2. To find a basis, we can write the pivots as linear combinations of the original vectors:
[1 -1 0 2] = [1 0 0 2] + [-1 1 0 0]
[0 1 -2 -1] = [0 1 -2 -1]
Therefore, a basis for S is {[1 0 0 2], [-1 1 0 0]}.
Visit here to learn more about subspace:
brainly.com/question/31691975
#SPJ11
A plumber charges $25 for a service call plus $50 per hour of service. Write an equation in slope-intercept form for the cost, C, after h hours of service. What will be the total cost for 8 hours of work?
Answers
Answer:
C(h) = 50h + 25
$425
Step-by-step explanation:
Et the plumber works for h hours.
Cost of one hour = $50
Therefore, cost of h hours = $50h
Total cost = cost of h hours + plumber service call charge
C(h) = 50h + 25 (required equation)
Plug h = 8
C(8) = 50* 8 + 25 = 400 + 25 = $425
Roxy used a calculator to evaluate (18 + 2) × (49 – 34) – 63 ÷ 9 by entering C 18 + 2 * 15 – 7 into a calculator. Which statement is true?
The calculator will show the correct value because 2 should be multiplied by 15 first.
The calculator will show the correct value because 7 should be subtracted from 18 first.
The calculator will show an incorrect value. She should have added 18 and 2 and then entered C 20 * 15 – 7 into the calculator.
The calculator will show an incorrect value. She should have subtracted 7 from 15 and then entered C 18 + 2 * 8 into the calculator.
Answers
\( \large\overbrace{\underbrace{\underline{\boxed{ \sf \: Aиѕωεя ☂}}}}\)
The Correct choice is C
The calculator will show an incorrect value, because she should have added 18 and 2 then entered 20 * 15 - 7 into the calculator.
I hope that explains it since we have to solve what's given in the bracket first.
Which statements are true about the comparisonbetween the two figures? Check all that apply.The scale factor is 2.The scale factor isOThe perimeter of the model is the product of thescale factor and the perimeter of the originalrectangle.The area of the reduced figure is half the area ofthe original figure.The area of the reduced figure istimes thearea of the original figure.Done0000000

Answers
the sacale factor is 1/2 because the sides are cut in half
The perimeter of the model is the product of thescale factor and the perimeter of the original rectangle. Because the origigale perimeter is 6+6+2+2=16 , and if multiply by 1/2 the perimeter is 8, this number is right because 3+3+1+1=8
The area of the reduced figure is 1/4 times the area of the original figure. because the original area is 6x2=12 and multiply by 1/4 is 3, the number is right because 3x1=3
point) We say a definite integral is improper if one is infinite, or if the is infinite.
Answers
A definite integral is said to be improper if one or both of the limits of integration are infinite, or if the integrand function has a vertical asymptote within the interval of integration.
In other words, an improper integral is one that cannot be evaluated using the usual techniques of integration, such as the fundamental theorem of calculus, because it involves infinite limits or a function that is not integrable over the interval.
For example, the definite integral of f(x) = 1/x from 1 to infinity is an improper integral because the upper limit of integration is infinity, which is not a finite number. Similarly, the definite integral of f(x) = ln(x) from 0 to 1 is an improper integral because the lower limit of integration is 0, and the function has a vertical asymptote at x=0.
To evaluate improper integrals, we use limit processes to determine whether the integral converges (has a finite value) or diverges (has an infinite value). If the integral converges, we can find its value by taking the limit of a related integral as one or both of the limits of integration approach infinity or zero.
To learn more about Definite integral :
https://brainly.com/question/30074848
#SPJ4
Given the function f(x) = 4x + 10 and g(x), which function has a greater slope?
x g(x)
2 5
4 7
6 9
f(x) has a greater slope.
g(x) has a greater slope.
The slopes of f(x) and g(x) are the same.
The slope of g(x) is undefined.
Answers
Explanation: when graphing g(x) on a graphing calc, you will see that the slope is 2/2, which is less than a slope of 4.
Hope this helps!!
answer; #13,#14,#15. ((PLEASE HELP ME)). ((due today)).




Answers
The domain and range of f(x) = -24 are given as follows:
Domain: all real values.Range: {-24.}The domain and range of f(x) = 0.5(x + 4)² - 11 are given as follows:
Domain: all real values.Range: f(x) >= -11.The range of y = -2x² + 12x - 13 is given as follows:
y <= 5.
How to obtain the domain and the range of a function?The domain of a function is the set that contains all the input values that can be assumed by the function.
As neither of the functions in this problem have any restriction, the domain is all real values for the two of them.
The range of a function is the set that contains all the output values that can be assumed by the function.
The ranges are given as follows:
Constant function: single constant, hence the {}.Quadratic functions: negative infinity to vertex (concave down) and vertex to positive infinity (concave up).More can be learned about the domain and the range of a function at https://brainly.com/question/30248800
#SPJ1
(a-b) ( a+b) simplify
Answers
Answer:
\(a^2 - b^2\)
Step-by-step explanation:
1. \((a)(a)+(a)(b)+(-b)(a)+(-b)(b)\)
2. \(a^2 + ab - ab - b^2\)
3. \(a^2 - b^2\)
factor the polynomial
x^2y + x
Answers
Answer:
x(xy + 1)
Step-by-step explanation:
The two terms have the common factor x.
x²y + x = x(xy + 1)
What is mAngleDFC?
45°
80°
125°
135°
I want a step by step explanation of why it's 80.

Answers
Answer:
the answer is 80
Step-by-step explanation:
or, angleAFE =angleBFD [V.O.A]
or, 125=45+DFC
or, 125-45=DFC
or, 80 =DFC
Using the concepts of straight angle, ∠DFC = 80°.
What is a straight angle?A straight angle is an angle equal to 180 degrees. It is called straight because it appears as a straight line.
Since AD is a straight line.
∠AFE + ∠EFD = 180°
125° + ∠EFD = 180°
∠EFD = 180° - 125° = 55°
Now, EB is a straight line.
∠EFD + ∠DFC + ∠CFB = 180°
55° + ∠DFC + 45° = 180°
∠DFC = 180° - 100° = 80°
Learn more about straight angle here
https://brainly.com/question/9662298
#SPJ3
you have a fair die, with six faces containing the numbers 1,2,3,4,5,6. are the two events a and b, defined below, mutually exclusive? explain your answer.
Answers
you have a fair die, with six faces containing the numbers 1,2,3,4,5,6. are the two events a and b then A and B are exhaustive.
Given
A= { 1,2,4}
B= { 2,3,4,5,6}
C= { 3,4}
D= { 2,4,5}
Solving (a): The mutually exclusive events
These are events that have no common or mutual elements
Events A to D are not mutually exclusive because each of the events have at least 1 common element with one another.
Solving (b): Exhaustive events.
Two events X and Y are said to be exhaustive if:
S= P(X n Y)
i.e. if the sample space equals the intersection of X and Y
For events A to D, we have:
AnB= { 1,2,3,4,5,6}
and the sample space is:
S= {1,2,3,4,5,6}
By comparison;
A n B= S
Hence, A and B are exhaustive.
learn more about of dice here
https://brainly.com/question/24129793
#SPJ4
To decide whether the slope coefficient indicates a "large" effect of X on Y. you look at the economic importance implied by the slope coefficient value of the intercept size of the slope coefficient regression R^2
Answers
The economic significance suggested by the slope coefficient helps you determine whether the coefficient implies a "big" effect of X on Y.
what is slope ?A line's steepness and direction are determined by the slope of the line. Without actually using a compass, determining a line's slope in a coordinate plane can aid in determining whether the line is parallel, perpendicular, or not. Calculated using the slope of a line formula, the ratio of "vertical change" to "horizontal change" between two different locations on a line is determined. The increase divided by the run, or the ratio of the rise to the run, is known as the line's slope. In the coordinate plane, it describes the slope of the line.
Given
The slope coefficient suggests economic significance.
The economic significance suggested by the slope coefficient helps you determine whether the coefficient implies a "big" effect of X on Y.
To know more about slope visit :-
https://brainly.com/question/3605446
#SPJ4
Solve for x.
8x-132
5x+8
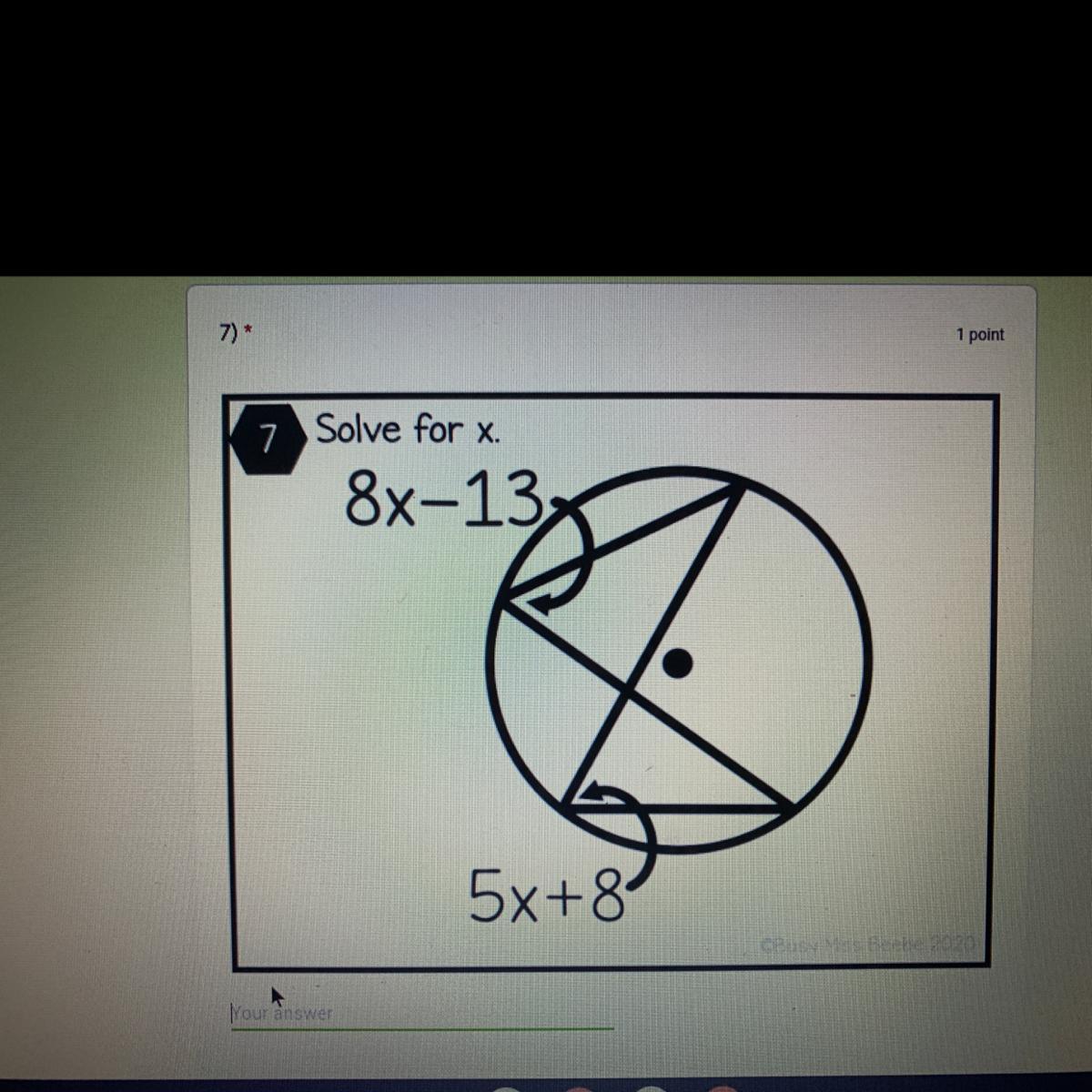
Answers
8x-132=5x+8
+132
8x=5x+140
-5x
3x=140/3
Devon is hired by the city to create a scale mural of a local park. devon is exactly 6 feet tall but in the mural, he is 4.5 feet tall. if the tree in the park is 30 feet tall, how tall should the tree be in the mural?
Answers
The tree should be 22.5 feet tall in the mural.
To determine the height of the tree in the mural, we can set up a proportion based on the scale ratio between Devon's height and the height of the tree.
Let's denote the height of the tree in the mural as 'x'.
According to the given information:
Devon's actual height: 6 feet
Devon's height in the mural: 4.5 feet
Tree's actual height: 30 feet
Setting up the proportion:
(Devon's height in the mural) / (Devon's actual height) = (Tree's height in the mural) / (Tree's actual height)
Substituting the given values:
4.5 feet / 6 feet = x / 30 feet
To solve for 'x', we can cross-multiply:
4.5 feet * 30 feet = 6 feet * x
135 feet = 6x
Divide both sides by 6:
x = 135 feet / 6
Simplifying the division:
x = 22.5 feet
Therefore, in the painting, the tree should stand 22.5 feet tall.
Learn more about proportion on:
https://brainly.com/question/870035
#SPJ11
PLEASE HELP ME ASAP IT IS DUE IN 3 MINUTES :((((((((((
Answers
Please help me with this!! It involves a pie chart and percentages.

Answers
Answer:
65.5%
Explanation:
total number of students = 10+8+3+8 = 29
8+8+3 = 19 = number of students that did not choose football
(19/29)*100 = 65.51724138
rounded to nearest tenth = 65.5%
Answer:
65.5%
Step-by-step explanation:
To find the answer to this question, we have to find the number of people considering both attributes of the question. This is the number of people who do football and the number of people who do any type of sport in general.
The number of people who play any sport:
Wrestling = 8
Lacrosse = 3
Baseball = 8
Football = 10
8 + 3 + 8 + 10 = 29
The number of people who do not play football
29 - 10 = 19
Divide our values
19 ÷ 29 = 0.65517
Convert into percentage
To convert a decimal into a percentage we have to multiply the decimal by 100
0.65517 × 100 = 65.517
65.5 to the nearest tenth
Hope this helps, have a lovely day! :)
7 x 7 ( __ x 7 ) + ( 2 x 7 )
= __ + 14
=
Answers
Answer:
Step-by-step explanation:
1) 5
2) 63
????
What is 3 examples of a rate?
Answers
Answer:
Step-by-step explanation: For example, if a 12 ounce can of corn costs 55 cents the rate is 55 cents for 12 ounces. The first term in ratio is measured in cents the second term in ounces
HELP PLEASE JJFFNFNFNF

Answers
Answer:
A.
17 vs 18, not trueB.
TrueC.
Mean:
(4*5 + 5*3 + 6*2 + 12 + 13*4 + 14*2)/17 = 8.17Median:
6Mean ≠ median, not true
D.
14 - 4 = 109 - 3 = 6, 10 > 6, not trueAnswer:
B
Step-by-step explanation:
Option B is correct because from the data it's visible that all the data are around 6 miles in other words clustered. In Class A half of them are on left and half are on right. Option A is wrong because there are 17 students in class A and 18 students in class B.
Option C is wrong because the mean is 8.2 and the median is 6.
To find mean add up all the miles the students chose and divide by total students (4+4+4+4+4+5+5+5+6+6+12+13+13+13+13+14+14)/17 = 8.2
To find the median line up all the numbers and find the one in middle. It's 6.
Option D is wrong because the range for class A is (14-4)=10
and class B is (9-3)=6. So the range of class A is greater than class B.
To find range maximum value-minimum value
Which inequality is represented by this graph

Answers
Answer:
The answer is C
Step-by-step explanation:
7652 divided by 12.3
Answers
ANSWER
622.113821138 is the answer
Answer:
622.1138
Step-by-step explanation: