What is the answer of 9^2 • 9^3
Answers
Answer:
9^5
Step-by-step explanation:
the number you're multiplying stays the same and you add your powers I believe.
so it's basically 9•1 and the ^2+^3=^5
Answer:
\(\boxed {\tt 9^{5}}\)
Step-by-step explanation:
When multiplying exponents, the base stays the same and the exponents are added.
\(a^x*a^y=a^{x+y}\)
We are given the expression:
\(9^2*9^3\)
The base is 9, and it will stay the same. The exponents, 2 and 3, must be added.
Exponents: 2, 3 Add them: 2+3=5\(9^{2+3}\)
\(9^5\)
The answer to 9²*9³ is 9⁵
Related Questions
How do I do this problem?

Answers
Answer: you would put x and y in their places
and solve it, remember, Ax+By+C=0
but in this case its Dx+Ey+F
Nadie bought 4.3 pounds of hem on Tuesday and 1.7 pounds of ham on Wednesday. She spent a total of $41.94. What was the price of the ham per pound?
Answers
Answer:
$6.99
Step-by-step explanation:
4.3+1.7 pounds is 6 pounds. The price per pound would be $41.94 divided by 6. Therefore, $6.99
calculate the probability the proportion of the 30 americans sampled that agree climate change is an immediate threat to humanity exceeds 35%?
Answers
The probability that the proportion of the 30 Americans sampled that agree climate change is an immediate threat to humanity exceeds 35% is approximately 82.38%.
To calculate the probability that the proportion of Americans who agree that climate change is an immediate threat to humanity exceeds 35%, we need to use the central limit theorem and the normal distribution.
Assuming the sample of 30 Americans is representative of the population, we can calculate the sample proportion as the number of individuals in the sample who agree divided by the total sample size. Let's assume that the sample proportion is p'.
To calculate the probability of the proportion exceeding 35%, we need to find the z-score of the value 0.35 using the formula:
z = (p' - p) / √[p * (1 - p) / n]
where p is the population proportion (which we don't know), and n is the sample size (30 in this case). We can use p' as an estimate of p.
Once we find the z-score, we can use a standard normal distribution table or a calculator to find the probability that the z-score is greater than the value we calculated. This probability is the probability that the proportion of Americans who agree that climate change is an immediate threat to humanity exceeds 35%.
For example, if p' = 0.4, then the z-score is:
z = (0.4 - 0.35) /√ [0.35 * (1 - 0.35) / 30] = 1.03
Using a standard normal distribution table, we can find that the probability of a z-score being greater than 1.03 is approximately 0.8238, or about 82.38%.
To learn more about probability click on,
https://brainly.com/question/29035617
#SPJ4

I need help finding the lateral and surface area of this prism and if the answer is too big it can be rounded to the nearest tenth

Answers
Answer:
Lateral area = 647.1 \(in^{2}\)
Surface area = 1123.9 \(in^{2}\)
Step-by-step explanation:
This is a triangular prism
Shape of base: Triangle
h = Perpendicular height = 9 in
Lateral area of triangular prism:
= (Perimeter of triangle) × h
= (20 in + 25 in + 26.9 in) × (9 in)
Lateral area = 647.1 \(in^{2}\)
Surface Area of triangular prism:
= 2(Area of triangle) + Lateral area
m = perpendicular height of triangle:
Area of triangle = \(\frac{1}{2}\)×(base of triangle)×(m)
m is not provided, therefore area of triangle is calculated using Heron's formula:
Area of triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\)
where s = semi-perimeter of the triangle = \(\frac{a + b + c}{2}\)
= \(\frac{20 + 25 + 26.9}{2}\)
= 35.95 in
∴ Area of triangle = \(\sqrt{35.95(35.95-20)(35.95 - 25)(35.95-26.9)}\)
= \(\sqrt{56822.7543}\) \(in^{2}\)
∴ Surface Area =[\(2(\sqrt{56822.7543}) + 647.10\)] \(in^{2}\)
= 1123.85 \(in^{2}\)
Surface Area = 1123.9 \(in^{2}\) (Rounded to the nearest tenth)
please helpppp!!!!!!!

Answers
EXPLANATION: 15 is equivalent to x as 3 is equivalent to 10. 10 divided by 3 = 3.33. We would multiply 15 by 3.33 to find what x would be. 15 x 3.33 = 50.
A part of exponential function fis graphed on the grid.
5
Which inequality best represents the domain of the part shown?
A x > 1
B y > 1
C X - 2
D Y > -2

Answers
The domain is the x-values used by the graph, so you want to see how your graph lines up with respect to the x-axis.
This graph starts out with an x-value of 2 (although it doesn't really use 2, since it's an open circle) and then continues to the right forever.
The domain is x > –2.

Iggy is practicing for a marathon by running laps on the
track at school. Each lap covers 0.7 kilometers, and he
has already run 19.6 kilometers. How many laps does he
need to run if he wants to complete 91 kilometers?
Answers
Apply Euler's method twice to approximate the solution to the initial value problem on the interval 0,2 first with step size h = 0.25, then with step size h = 0.1. Compare the 1 three-decimal-place 1 with the value of y 2 of the actual solution. values of the two approximations at x = y' = - 3x²y, y(0) = 10, y(x) = 10 e −x³
Answers
The approximations of the solution at x = 1 using Euler's method with step sizes h = 0.25 and h = 0.1 are 9.625 and 9.997, respectively. Neither approximation matches the actual solution y₂ ≈ 5.987, but the approximation with h = 0.1 is closer to the actual value.
To approximate the solution to the initial value problem using Euler's method, we first need to express the problem in the form of a first-order differential equation. The given initial value problem is:
dy/dx = -3x²y, y(0) = 10.
We can rewrite this equation as y' = -3x²y. The actual solution to this problem is given by y(x) = 10e^(-x³).
Now, let's apply Euler's method twice with two different step sizes to approximate the solution on the interval [0, 2].
1. Using step size h = 0.25:
We start at x = 0 with y = 10 (initial condition). The formula for Euler's method is:
yₙ₊₁ = yₙ + h * f(xₙ, yₙ),
where yₙ represents the approximation of y at the nth step, xₙ = nh represents the value of x at the nth step, and f(xₙ, yₙ) represents the value of the derivative at the nth step.
Applying Euler's method with h = 0.25, we get:
x₀ = 0, y₀ = 10.
x₁ = 0 + 0.25 = 0.25,
y₁ = y₀ + 0.25 * f(x₀, y₀) = 10 + 0.25 * (-3 * 0² * 10) = 10.
Now, for the second step:
x₁ = 0.25, y₁ = 10.
x₂ = 0.25 + 0.25 = 0.5,
y₂ = y₁ + 0.25 * f(x₁, y₁) = 10 + 0.25 * (-3 * 0.25² * 10) = 10 - 0.375 = 9.625.
2. Using step size h = 0.1:
Following the same process, we can calculate the approximations:
x₀ = 0, y₀ = 10.
x₁ = 0 + 0.1 = 0.1,
y₁ = y₀ + 0.1 * f(x₀, y₀) = 10 + 0.1 * (-3 * 0² * 10) = 10.
For the second step:
x₁ = 0.1, y₁ = 10.
x₂ = 0.1 + 0.1 = 0.2,
y₂ = y₁ + 0.1 * f(x₁, y₁) = 10 + 0.1 * (-3 * 0.1² * 10) = 10 - 0.003 = 9.997.
Comparing the approximations at x = 1 with the actual solution y₂ = 10e^(-1³) ≈ 5.987, we have:
For h = 0.25: Approximation = 9.625
For h = 0.1: Approximation = 9.997
As we can see, both approximations differ from the actual solution, but the approximation with a smaller step size (h = 0.1) is closer to the actual value.
To know more about Euler's method, refer here:
https://brainly.com/question/30699690#
#SPJ11
A clothing store offers a 50% discount at the end of
each week that an item remains unsold. Patrick
wants to buy a shirt at the store and he says, "I've
got a great idea! I'll wait two weeks, have 100%
off, and get it for free!" Explain to your friend
Patrick why he is incorrect and find the correct
percent of discount on the original price of a shirt.
Answers
Let the original price of the item be X.
In one week, the price is halved and becomes (1/2)X.
In two weeks, the price is halved again and becomes (1/4)X, which is only 75% off.
Please answer this easy math question!! 13 pts!!

Answers
7b-8+6b+7=90
Combine like terms:
13b-1=90
Add 1 to both sides:
13b=91
Divide 13 to both sides:
b=7
Hope this helped!
Answer:
Step-by-step explanation:
The problem shows a 90° angle split by a ray, we know that both angles are equal to 90° because the whole is equal to the sum of its parts therefore adding 6b+7 and 7b-8 gives us 90° which is simplified as
13b°-1°= 90°
add 1 to both sides
13b°-1° + 1° = 90° +1°
13b° = 91°
divide by 13
13b°/13 = 91°/13
b= 7°

Find parametric equations for the line. (Use the parameter t.) The line through the points (0,1/2,1) and (5,1,−6) (x(t),y(t),z(t))= Find the symmetric equations.
2x−2=y−5/5=z+6/−7
5+5x=1+y/2=−6−7z
x−5=2y−2=z+6
x−5/5=2y−2=z+6/−7
x+6/−7=2y−2=z−5/5
Answers
The parametric equations for the line passing through the points (0, 1/2, 1) and (5, 1, -6) are: x(t) = 5t, y(t) = 1/2 + t/2, and z(t) = 1 - 7t. The symmetric equations for the line are: x/5 = (y - 1/2)/5 = (z - 1)/(-7).
The parametric equations for the line passing through the points (0, 1/2, 1) and (5, 1, -6) can be expressed as:
x(t) = 5t
y(t) = 1/2 + t/2
z(t) = 1 - 7t
The symmetric equations for the line can be derived as follows:
(x - 0)/5 = (y - 1/2)/(5 - 0) = (z - 1)/(-6 - 1)
Simplifying, we get:
x/5 = (y - 1/2)/5 = (z - 1)/(-7)
Therefore, the symmetric equations for the line are:
x/5 = (y - 1/2)/5 = (z - 1)/(-7)
To know more about parametric equations refer here:
https://brainly.com/question/29275326#
#SPJ11
simplify this equation 5.9 - 10 + 2.84
Answers
Answer:
8.74 - 10
Step-by-step explanation:
combine like terms
positive 5.9 combined with positive 2.84 equals 8.74
so the answer is 8.74 - 10
Answer:
Step-by-step explanation:
5.9 - 10 +2.84 = -1.26
so first, 5.9 - 10 = -4.1
then -4.1 + 2.84 = -1.26
so -1.26 is your answer.
nominal decisions can be broken into which two distinct categories?
Answers
Answer:
Nominal decisions can be broken into two distinct categories: dichotomous decisions and polychotomous decisions.
i need some help with this problem i don’t really understand it

Answers
Answer:
-34x+29
Step-by-step explanation:
\(7(5-x)-3(9x+2)=7.5-7x-3.9x-3.2=35-7x-27x-6\\=-34x+29\)
find the measure of angle 7

Answers
Answer:
63°
Step-by-step explanation:
Knowing that opposite angles are equivalent, we can easily say that ∠3 is equivalent to 63°. ∠1 and ∠4 are the complements of the given angle and ∠3, so their measures are also the same and are equivalent to 180°-63°=117°.
Since the two horizontal lines are parallel, ∠6 is equivalent to ∠3, so it too is 63°. Its complements, ∠5 and ∠8, are thus equivalent to the complements of ∠1 and ∠4, and thus they are 117°. Lastly, since opposite angles are equivalent, ∠6 is equivalent to ∠7, and so ∠7 is also 63°.
What is the difference from c(2,-1) to d(5,3) a.5 units b.25 units c. 1 unit d.
Answers
====================================================
Explanation:
The two points given are
C = (x1,y1) = (2,-1)
D = (x2,y2) = (5,3)
Use the distance formula
\(d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\\\\d = \sqrt{(2-5)^2 + (-1-3)^2}\\\\d = \sqrt{(-3)^2 + (-4)^2}\\\\d = \sqrt{9 + 16}\\\\d = \sqrt{25}\\\\d = 5\\\\\)
The distance from C to D is 5 units. This is the same as saying segment CD is 5 units long.
If the length of the cushion measures 12 in, the width measures 10 in, and the height measures 3 in, how much fabric does Greg need to cover the cushion? A. 360 sq in B. 186 sq in C. 372 sq in D. 720 sq in
Answers
If the length of the cushion measures 12 in, the width measures 10 in, and the height measures 3 in, 372 sq in. fabric Greg needed to cover the cushion. The correct option is C, 372 sq in.
To determine the amount of fabric needed to cover the cushion, we need to calculate the surface area of the cushion. The surface area of a rectangular cushion is given by the formula: 2lw + 2lh + 2wh, where l is the length, w is the width, and h is the height of the cushion.
Plugging in the given measurements, we get:
2(12 x 10) + 2(12 x 3) + 2(10 x 3) = 240 + 72 + 60 = 372 sq in.
Therefore, Greg needs 372 square inches of fabric to cover the cushion.
Visit here to learn more about measurements:
brainly.com/question/27122947
#SPJ11
Verify the identity:
sin²x - sin x/1- cos²x = sin x - 1/sin x
Answers
Answer:
See below for proof
Step-by-step explanation:
\(\displaystyle \frac{\sin^2x-\sin x}{1-\cos^2x}\\\\=\frac{\sin^2x-\sin x}{\sin^2x}\\\\=\frac{\sin x-1}{\sin x}\)
Thus, the identity is proven. Note that \(\cos^2x+\sin^2x=1\) by the Pythagorean Identity and canceling out \(\sin x\) in the second step gets us our correct answer.
Let x represent any year. Write an inequality in terms of x and 1610
that is true only for values of x that represent years after the year the Mali Empire fell.
Answers
The year of the empire fell = 1610.
We are given x as a variable that represents the year after the given year 1610.
We need to setup an inequality for this situation.
Please note: The year after the year number 1610 will have a number that greater than 1610.
Let us make a statement for inequality to be written.
"The year after the 1610 is greater than 1610".
The year after the 1610 is x and gerater than symbol is >.
So, we can setup an inequality as:
x > 1610 : Read as x is greater than 1610.
The equilateral triangle shown has perimeter 45 cm. How to find its side length?
Answers
Answer:
15 cm
Step-by-step explanation:
An equilateral triangle has all 3 sides equal, so you can say the length of one side is x. Then, the perimeter would be 3x. This means:
3x = 45
divide both sides by 3
x = 15 cm
What is the answer for both?
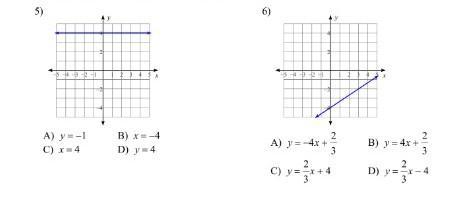
Answers
Answer:
5. D
6. I think D. Because is y=mx+b and b is y the intercept in y. Y= 0-4 and replacing the -4 would remain at the end
What is the equation!!

Answers
Answer:
y = -5x - 2
Step-by-step explanation:
We have to use slope intercept form which is y = mx + b
mx is the slope and b is the y intercept. Let's start with the y intercept. The y intercept on this graph is -2 so lets see what it looks like to far
y = mx - 2
Next, we find the slope which is -5
y = -5x - 2
Answer:
y=-5x+-2
Step-by-step explanation:
Does anyone know this?

Answers
Answer:
obtuse scalene
Step-by-step explanation:
Answer:
Obtuse Scalene
Step-by-step explanation:
all the sides have different numbers
Assume that A + T/G + C equals 0.5 in one strand of DNA. What is the ratio of these bases in the complementary strand?
Answers
The overall ratio of A + T/G + C in the complementary strand is 0.5.
This is because the bases A and T, and G and C, always pair together in DNA. Therefore, if one strand of DNA has a ratio of 0.5 for A + T/G + C, the complementary strand will also have the same ratio.
To further explain, let's look at the individual bases. If A + T = 0.5, this means that the ratio of A to T is 1:1. Similarly, if G + C = 0.5, this means that the ratio of G to C is also 1:1. Since A always pairs with T, and G always pairs with C, the complementary strand will also have a 1:1 ratio for these bases. Therefore, the overall ratio of A + T/G + C in the complementary strand will also be 0.5.
You can learn more about complementary DNA strands at: brainly.com/question/29776082
#SPJ11
Given right triangle ABC with altitude BD drawn to hypotenuse AC. If AD = 25
and DC 25, what is the length of BD?

Answers
Answer:
25
Step-by-step explanation:
The required value of altitude BD is 25 units, which is determined by the geometric theorem.
What is the right triangle?A right triangle is defined as a triangle in which one angle is a right angle or two sides are perpendicular.
As we know that the geometric theorem states that h = √(ab),
where h is the altitude of a right triangle, a and b are the segments formed when the altitude divides the hypotenuse of a right triangle.
We have to determine the value of altitude y
As per the given figure, a = 25, and b = 25
Substitute the values in the formula, and we get
x = √(25 × 25)
x = √625
x = 25
Therefore, the measure of BD = 25.
Learn more about the right triangle here:
brainly.com/question/6322314
#SPJ2
What is 50% of 80? part percent
Answers
Answer:
40
Step-by-step explanation:
10% = 80 ÷ 10 = 8
50% = 8 x 5 = 40
Hope this helps!
Answer:
40
Explanation:
50% = 80 ÷ 2 = 40
Hope this helps!
the probability that a patient recovers from a stomach disease is .8. suppose 20 people are known to have contracted this disease. what is the probabi
Answers
We can use the binomial distribution formula to find the probability of how many people will recover from the stomach disease out of the 20 people who have contracted it.
The probability that a patient recovers from a stomach disease is .8, and we know that 20 people have contracted this disease. To find the probability of how many of these 20 people will recover, we can use the binomial distribution formula.
The binomial distribution formula is P(X=k) = (n choose k) * p^k * (1-p)^(n-k), where X is the number of successes, k is the specific number of successes we want to find, n is the total number of trials, p is the probability of success, and (n choose k) represents the number of combinations of n items taken k at a time.
In this case, we want to find the probability that out of the 20 people with the disease, k of them will recover. We can set n = 20, p = 0.8, and k can range from 0 to 20.
To find the probability that exactly 10 people will recover, we plug in n = 20, p = 0.8, and k = 10 into the formula: P(X=10) = (20 choose 10) * 0.8^10 * (1-0.8)^(20-10) = 0.0687, or approximately 6.87%.
To find the probability that at least 15 people will recover, we need to add up the probabilities of 15, 16, 17, 18, 19, and 20 people recovering. We can use a calculator or a table to find each individual probability and add them up. The total probability is approximately 0.9894, or 98.94%.
Overall, we can use the binomial distribution formula to find the probability of how many people will recover from the stomach disease out of the 20 people who have contracted it.
for more questions on binomial distribution
https://brainly.com/question/24756209
#SPJ11
In working with two variables related by a regression equation, the _________________ in a variable is the amount that it changes when the other variable changes by exactly one unit.
Answers
In working with two variables related by a regression equation, the marginal change in a variable is the amount that it changes when the other variable changes by exactly one unit.
What is the regression equation for two independent variables?The regression equation, Y'i = b₀ + b₁X₁\(_{i}\) + b₂X₂\(_{i}\), in three dimensions, defines a plane. If you computed all possible values of Y for all possible values of X1 and X2, all of the points would fall on a two-dimensional surface.If y is the dependent variable and x is the independent variable in a regression analysis, the relationship is described as the regression of y on x. A simple equation known as the regression equation can be used to represent the relationship.Learn more about regression equation at: brainly.com/question/29582333
#SPJ4
add and subtract function PLS HELP!!!!

Answers
Answer:
The first option:
\(6x^{2} -4x+6\)
Step-by-step explanation:
Trust me I am right.
If you need work please ask!
Have a nice day!
A person can read 24 pages of a book in 1/3 of an hour. What is this person's reading rate in pages per hour?
72
48
12
8
Answers
20 mins - 24 pages
hour (60 mins) - 24x3 = 72