What is the area of a circle with a radius of 6 inches?
9 pi in^2
12 pi in^2
36 pi in^2
81 pi in^ 2
Answers
Answer:
Area of circle = πr² ( Putting π = 22/7) Area = 3.14×6×6Area = 113.04Step-by-step explanation:
If you like my answer than please mark me brainliest thanks
Related Questions
Enter the exact values of the trigonometric ratios in the boxes.
sin 45°
cos 30
tan 60
=

Answers
The required value of trigonometric ratios is,
sin 45° = 1/\(\sqrt{2}\)
cos 30 = \(\sqrt{3}\)/2
tan 60 = 1/ √3
We know that,
Trigonometric ratios are based on the value of the ratio of sides of a right-angled triangle and contain the values of all trigonometric functions. The trigonometric ratios of a given acute angle are the ratios of the sides of a right-angled triangle with respect to that angle.
Therefore,
sin 45° = 1/\(\sqrt{2}\)
cos 30 = \(\sqrt{3}\)/2
tan 60 = 1/ √3
To learn more about triangles visit:
brainly.com/question/1058720
#SPJ1
Over the last three evenings, Lucy received a total of 107 phone calls at the call center. The second evening, she received 3 times as many calls as the third evening. The first evening, she received 7 more calls than the third evening. How many phone calls did she receive each evening?
Answers
Answer:
1st evening = 7 + 20 = 27 calls
2nd evening = 3 (20 ) = 60 call
3rd evening = 20 calls
Step-by-step explanation:
total calls for the last three evenings = 107 phone calls
2nd evening = 3x as many calls as the 3rd evening
1st evening = 7 more calls than the 3rd evening.
find:
how many calls did she receive each evening?
let T (total) = 107
let x = 3rd evening.
let 2nd = 3x
let 1st = (7 + x)
T = 1st + 2nd + 3rd
107 = (7 + x) + 3x + x
107 - 7 = 5x
100 = 5x
x = 100 / 5
x = 20
therefore,
1st evening = 7 + 20 = 27 calls
2nd evening = 3 (20 ) = 60 call
3rd evening = 20 calls
Answer:
1st = 27 calls
2nd = 60 call
3rd = 20 calls
Step-by-step explanation:
total calls = 107 phone calls
2nd = 3x
1st = 7 + 3x
T (total) = 107
T = 1st + 2nd + 3rd
107 = (7 + x) + 3x + x
107 - 7 = 5x
100 = 5x
x = 100 / 5
x = 20
so,
1st = 7 + 20 = 27 calls
2nd = 3 (20 ) = 60 call
3rd = 20 calls
A student researcher compares the ages of cars owned by students and cars owned by faculty at a local state college. A sample of 263 cars owned by students had an average age of 7.25 years. A sample of 291 cars owned by faculty had an average age of 7.12 years. Assume that the population standard deviation for cars owned by students is 3.77 years, while the population standard deviation for cars owned by faculty is 2.99 years. Determine the 90% confidence interval for the difference between the true mean ages for cars owned by students and faculty. Step 1 of 3: Find the point estimate for the true difference between the population means.
Answers
Answer:
The point estimate for the true difference between the population means is 0.13.
The 90% confidence interval for the difference between the true mean ages for cars owned by students and faculty is between -0.35 years and 0.61 years.
Step-by-step explanation:
To solve this question, before building the confidence interval, we need to understand the central limit theorem and subtraction between normal variables.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Subtraction between normal variables:
When we subtract two normal variables, the mean is the subtraction of the means while the standard deviation is the square root of the sum of the variances.
A sample of 263 cars owned by students had an average age of 7.25 years. The population standard deviation for cars owned by students is 3.77 years.
This means that:
\(\mu_s = 7.25, \sigma_s = 3.77, n = 263, s_s = \frac{3.77}{\sqrt{263}} = 0.2325\)
A sample of 291 cars owned by faculty had an average age of 7.12 years. The population standard deviation for cars owned by faculty is 2.99 years.
This means that:
\(\mu_f = 7.12, \sigma_f = 2.99, n = 291, s_f = \frac{2.99}{\sqrt{291}} = 0.1753\)
Difference between the true mean ages for cars owned by students and faculty.
Distribution s - f. So
\(\mu = \mu_s - \mu_f = 7.25 - 7.12 = 0.13\)
This is also the point estimate for the true difference between the population means.
\(s = \sqrt{s_s^2+s_f^2} = \sqrt{0.2325^2+0.1753^2} = 0.2912\)
90% confidence interval for the difference:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1 - 0.9}{2} = 0.05\)
Now, we have to find z in the Ztable as such z has a pvalue of \(1 - \alpha\).
That is z with a pvalue of \(1 - 0.05 = 0.95\), so Z = 1.645.
Now, find the margin of error M as such
\(M = zs = 1.645*0.2912 = 0.48\)
The lower end of the interval is the sample mean subtracted by M. So it is 0.13 - 0.48 = -0.35 years
The upper end of the interval is the sample mean added to M. So it is 0.13 + 0.48 = 0.61 years.
The 90% confidence interval for the difference between the true mean ages for cars owned by students and faculty is between -0.35 years and 0.61 years.
If sin theta = -2/3 which of the following are possible?

Answers
Answer:
a
Step-by-step explanation:
The possible trigonometric function is option (C) \(sec \theta = \frac{3}{\sqrt{5} }\) and \(tan \theta = \frac{-2}{\sqrt{5} }\) is the correct answer.
What is trigonometry?Trigonometry is mainly concerned with specific functions of angles and their application to calculations. Trigonometry deals with the study of the relationship between the sides of a triangle (right-angled triangle) and its angles.
For the given situation,
The trigonometric function, sin θ = -2/3
We know that \(sin \theta = \frac{opposite}{hypotenuse}\)
So, opposite = -2, hypotenuse = 3
The other side of the right triangle adjacent side can be found by using the Pythagoras theorem,
\(adjacent=\sqrt{hypotenuse^{2} -opposite^{2} }\)
⇒ \(adjacent=\sqrt{3^{2} -(-2)^{2} }\)
⇒ \(adjacent=\sqrt{9-4 }\)
⇒ \(adjacent=\sqrt{5}\)
Now, \(cos \theta = \frac{adjacent}{hypotenuse}\) and \(tan \theta = \frac{opposite}{adjacent}\)
Then, \(cos \theta = \frac{\sqrt{5} }{3}\)
\(sec \theta = \frac{1}{cos \theta}\)
⇒ \(sec \theta = \frac{1}{\frac{\sqrt{5} }{3} }\)
⇒ \(sec \theta = \frac{3}{\sqrt{5} }\)
\(tan \theta = \frac{-2}{\sqrt{5} }\)
Hence we can conclude that the possible trigonometric function is option (C) \(sec \theta = \frac{3}{\sqrt{5} }\) and \(tan \theta = \frac{-2}{\sqrt{5} }\) is the correct answer.
Learn more about trigonometry here
https://brainly.com/question/16965914
#SPJ2
Find the surface area

Answers
Answer: 120 yds
Step-by-step explanation:
48+30+24+18+120 yds
Why do we choose 5% as a risk of making error and not 1%
Answers
In statistics, the risk of making an error is referred to as a significance level. A significance level represents the probability of making a Type I error, which occurs when a null hypothesis is rejected even though it is true.
The most common significance level used in statistical analyses is 0.05 or 5%. This means that there is a 5% chance of rejecting a true null hypothesis.
In general, the choice of significance level depends on the specific application and context of the statistical analysis.
The 5% significance level is commonly used in scientific research, particularly in the fields of medicine and psychology.
The choice of this level is based on a balance between the risk of making a Type I error and the risk of making a Type II error, which occurs when a null hypothesis is not rejected even though it is false.
A Type II error is often more serious than a Type I error since it may lead to incorrect conclusions about the relationship between variables or the effectiveness of a treatment or intervention.
A 5% significance level provides a reasonable balance between these two types of errors. However, in some situations, a higher or lower significance level may be more appropriate.
For example, in a clinical trial where the consequences of a Type II error are severe, a lower significance level may be used to reduce the risk of this type of error.
To learn more about : probability
https://brainly.com/question/251701
#SPJ8
carl has 1,064 legos. sharon has 19 time the amount of legos. how many legos does sharon have
Answers
1064 x
19
________
20216 legos
Sharon has 20216 legos
I am stuck please help with this graph.
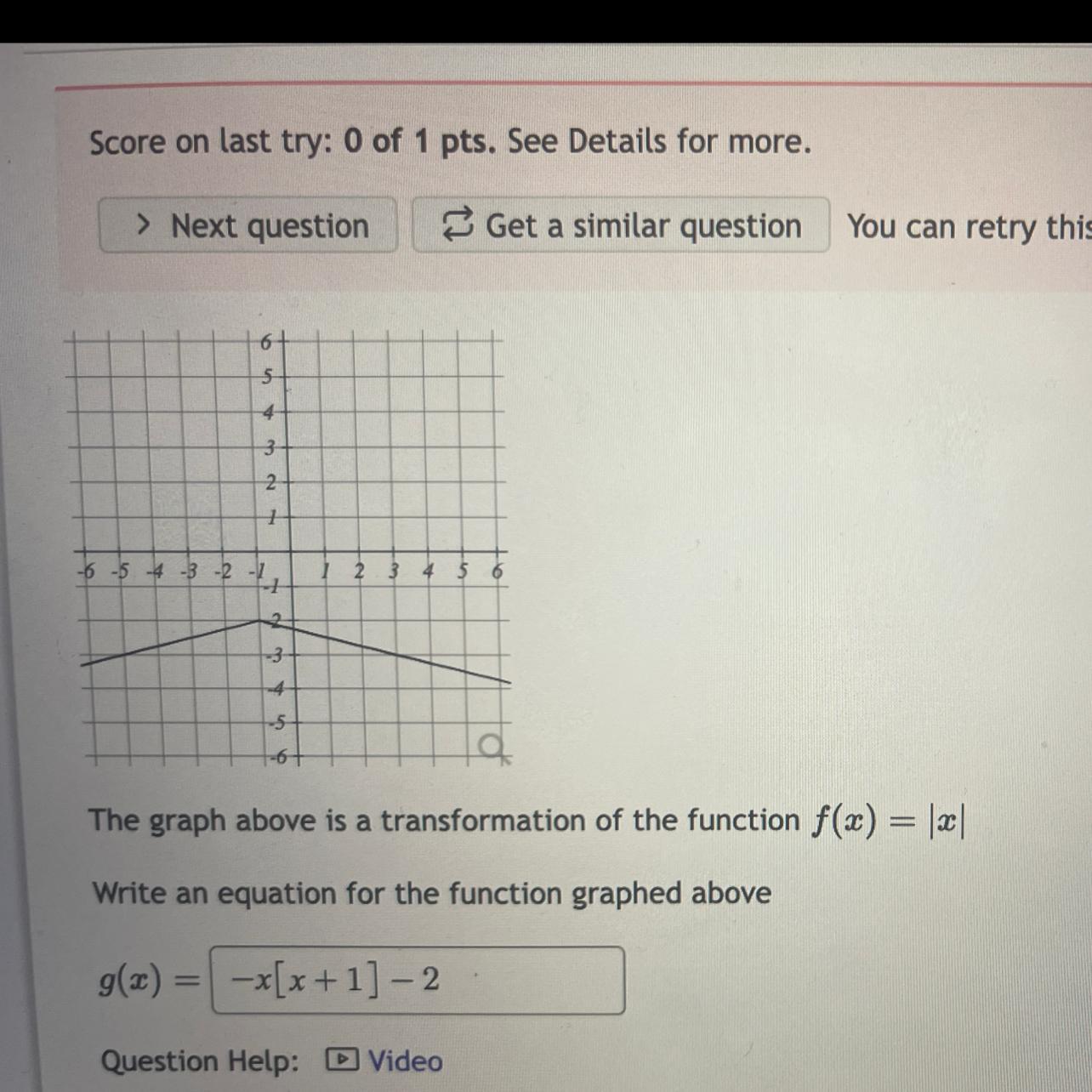
Answers
An equation for the function graphed above include the following: g(x) = -1/4|x + 1| - 2.
How to interpret and determine the equation of g(x)?By critically observing the graph of this absolute value function, we can reasonably infer and logically deduce that the parent absolute value function f(x) = |x| was vertically compressed by a factor of 1/4, reflected over the x-axis, followed by a vertical translation 2 units down, and then a horizontal translation to the left by 1 unit, in order to produce the transformed absolute value function as follows;
f(x) = |x|
y = A|x + B| + C
g(x) = -1/4|x + 1| - 2
In conclusion, the value of the variables A, B, and C are -1/4, 1, and 2 respectively.
Read more on absolute value function here: brainly.com/question/28308900
#SPJ1
Melissa runs a mile in 8 minutes 30 seconds. At this rate, how many full miles will she run in 45
minutes?
Answers
Answer:
Time measure: 8 miles = 30 seconds We are given 45 minutes × 60 seconds /30= 90 milesQUICK! 40 points. Consider this cone with the diameter measure of 17 inches.
A cone with diameter 17 inches and slant height of 22 inches.
What is the surface area of the cone?
SA = Pir2 + Pirl
A. 204Pi in.2
B. 259.25Pi in.2
C. 446.25Pi in.2
D. 663Pi in.2

Answers
259.25π in² is the surface area of the cone
The surface area of a cone can be calculated using the formula SA = πr² + πrl
where r is the radius and l is the slant height.
Given that the diameter is 17 inches, the radius (r) is half of the diameter, which is 17/2 = 8.5 inches.
The slant height (l) is given as 22 inches.
Substituting these values into the formula:
Surface Area = π(8.5)² + π(8.5)(22)
= 72.25π + 187π
= 259.25π
Therefore, the surface area of the cone is 259.25π in²
To learn more on Three dimensional figure click:
https://brainly.com/question/2400003
#SPJ1
find the output, y, when the input, is 5 y= 5x - 3

Answers
Ilke is deciding whether to take his girlfriend on a dinner date or on a movie date the probability of this having a successful dinner is 55%. the probability of this having a successful movie day is 0.45.
Which of these events is more likely?
Answers
Answer:
The dinner date
Step-by-step explanation:
PLEASE HELP!!!!! 20 POINTS FOR ANSWER!!!
A cylinder has a radius of 9 inches and is 12 inches tall. What is the approximate volume of the cylinder? Express the answer in terms of π. Recall the formula V = πr 2h. Show work.

Answers
Answer:
if you convert inches to cm...
Step-by-step explanation:
9inch=22.86cm
12inch=30.48cm
V=TTr²h
TT= 3.14
V= 3.14×22.86²×30.48
V= 50014.6cm³
if you don't convert inches to cm...
V=TTr²h
V=3.14 ×9×12
V=339.12cm³
Suppose we are minimizing the objective function value of a linear program. The feasible region is defined by 5 corner points. The objective function values at the five corner points are 4, 11, 7, 4, and 10. What type of solution do we have for this problem?.
Answers
The linear program shows that there are different attainable arrangements that accomplish the same ideal objective function value..
How to determine the solution to the objective function value of a linear programBased on the given data, since the objective function values at the five corner points are diverse, able to conclude that there's no one-of-a-kind ideal arrangement for this linear program.
The reality that there are numerous distinctive objective function values at the corner points suggests that there are numerous ideal arrangements or that the objective work isn't maximized or minimized at any of the corner points.
In this case, the linear program may have numerous ideal arrangements, showing that there are different attainable arrangements that accomplish the same ideal objective function value.
Learn more about Objective function value here:
https://brainly.com/question/14309521
#SPJ1
-5/2(6x+24)=x-12
please answer me!
Answers
Answer:
x= -3
Step-by-step explanation:
i hope its right
Identify the Vertex.

Answers
Answer: (2, 3)
Step-by-step explanation: This graph depicts a parabola. The vertex of a parabola is the point at the intersection of the parabola, and it is the line of symmetry. In other words, it is the point where the parabola crosses its axis of symmetry. Therefore, the ordered pair of (2, 3) represents the vertex of this graph.
What is the discriminant of the polynomial below?
9x^2 - 18x + 9
A. 0
B. 648
C. -306
D. -18

Answers
Which point is on the graph of f(x) = 5*?
O A. (0, 5)
O B. (0, 0)
• C. (5, 1)
O D. (1, 5)
Answer is (1,5)
Answers
The point that is on the graph of the function \(F(x) = 5^x\) is given by:
D. (1,5).
Which points are on the graph of the function?The function is defined by:
\(F(x) = 5^x\)
When x = 0, \(F(x) = 5^0 = 1\), hence point (0,1) is on the graph of the function.
When x = 1, \(F(x) = 5^1 = 5\), hence point (1,5) is on the graph of the function, which means that option D is correct.
When x = 5, \(F(x) = 5^5 = 3125\), hence point (5,3125) is on the graph of the function.
More can be learned about functions at https://brainly.com/question/26222939
#SPJ1
average age of 15 students of iub 11years if teacher is also included average age becomes 13 years how old is teachers
Answers
Answer: the teacher is 43
Step-by-step explanation: if you take 11 and multiply it by 15 you get 165 if you take 208 and divide it by 16 you get 13.
so basically you subtract 208 from 165 to get 43
An ice cream shop ordered a box of 700 cones. When they opened the box, they noticed 164 of the cones were broken. How many cones do they have left? *
Answers
Answer:
The answer would be 536 cones.
Step-by-step explanation:
You have to subtract 164 from 700.
700-164=536.
(4-2)^2x5+9
Answer+step by step
Answers
Answer:
4-2 = 2
2x5+9 = 19
2^19 = 2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2x2 = 524288
Answer:
29
Step-by-step explanation:
Use PEMDAS
P- Parenthesis
E- Exponents
M- Multiply
D- Divide
A- Add
S- Subtract
(4-2)^2×5+9 first you do parenthesis which is (4-2)=2
(2)^2×5+9 next the exponents (2)^2=4
4×5+9 now the multiplication, 4×5=20
20+9 And now finish it off with the addition
So the answer ends up being 29.
Use the given scale factor and the side lengths of the scale drawing to
determine the side lengths of the real object.
Scale factor: 4:1
10 in
6 in
b
8 in
Scale drawing
Object
A. Side a is 10 inches long, side bis 12 inches long, and side cis 14
inches long
B. Side a is 2 inches long, side bis 4 inches long, and side c is 6
inches long.
O
C. Side a is 24 inches long, side bis 32 inches long, and side cis 40
inches long.
d
D. Side a is 1.5 inches long, side bis 2 inches long, and side c is 2.5
inches long

Answers
Answer:
D for sure
Step-by-step explanation:
i dont know if you have time for this so i explain it in the comments if you need it
Answer:
the answer is D
Step-by-step explanation:
a 8 1/2 foot board Is cut Into 2 1/2 foot lengths. how many sections will you have
Answers
Answer:
3 whole but 3.4 as a decimal
Step-by-step explanation:
? Question
Drag the tiles to the correct boxes to complete the pairs.
Solve each equation using the square root property. Then, match the solutions to the equatio
Tiles
Help please

Answers
The solutions for the given equations are x = 9i , -9i , x = 2i,-2i ,
x = \(\sqrt{13}\) , - \(\sqrt{13}\) , x = \(\sqrt{14}\)i , - \(\sqrt{14}\)i .
Given equations ,
\(x^{2}\) + 81 = 0 ,\(x^{2}\)-22 = -26 , 3\(x^{2}\)-18=21 ,2\(x^{2}\) +15 = -13
What is Quadratic equation ?
quadratic equation can be defined as the equation which is in the form of a\(x^{2}\)+bx + c = 0 .
where a,b,c are constants .
By solving we get ,
\(x^{2}\) +81 = 0
\(x^{2}\) = -81
x = 9i , -9i
\(x^{2}\) - 22 = -26
\(x^{2}\) = -26 + 22
\(x^{2}\) = -4
x = 2i,-2i
3\(x^{2}\) - 18 = 21
3\(x^{2}\) = 18+21
3\(x^{2}\) = 39
\(x^{2}\) = 13
x = \(\sqrt{13}\) , - \(\sqrt{13}\)
2\(x^{2}\) +15 = -13
2\(x^{2}\) = -13-15
2\(x^{2}\) = -28
\(x^{2}\) = -14
x = \(\sqrt{14}\)i , - \(\sqrt{14}\)i
Hence the solutions for the given equations are x = 9i , -9i , x = 2i,-2i ,
x = \(\sqrt{13}\) , - \(\sqrt{13}\) , x = \(\sqrt{14}\)i , - \(\sqrt{14}\)i .
To learn more about Quadratic equations from the given link.
https://brainly.com/question/30098550
#SPJ1
g Find the required probabilities using the exponential density function f(t) = 1 λ e−t/λ, [0, [infinity]). The time t (in years) until failure of a component in a machine is exponentially distributed with λ = 3.5. Find the probabilities that the lifetime of a given component will be less than 1 year, more than 2 years but less than 4 years, and at least 5 years. (Round your answers to three decimal places.) (a) less than 1 year (b) more than 2 years but less than 4 years (c) at least 5 years
Answers
Answer:
(a) less than 1 year =0.751488
(b) more than 2 years but less than 4 years = 0.2458
(c) at least 5 years= 0.760331
Step-by-step explanation:
f(t) = 1 λ e−t/λ, [0, [infinity])
First we calculate the probability for an exponential random variable X with parameter λ
P (X= t) = ∫ 1 λ e−t/λ, dt
P (x=t) = e−t/λ,
λ = 3.5
Now P (X< 1 ) = ∫ 1 λ e−t/λ, dt [the limits are (-∞ to 1)]
= e−1/3.5= 0.751488
P ( 2<X< 4 ) = ∫ 1 λ e−t/λ, dt [ the limits are (2 to 4)]
=e−2/3.5- e−4/3.5
= e-0.57142-e-1.142857
= 0.5647-0.31890
= 0.2458
P (at least 5) = 1- P (x=5)
= 1-∫ 1 λ e−t/λ, dt [ the limits are (∞ to 5)]
= 1- e−5/3.5
= 1 - e-1.4285
= 1-0.239
= 0.760331
CAN SOMEONE PLEASE HELP ME WITH MY MATH ASAP PLEASE!!!!

Answers
Answer:
5
Step-by-step explanation:
The height of the largest triangle = √(9 * 25) = 3 * 5 = 15
y is the square root of (25^2 + 15^2)
y = √(625 + 225)
y = √850
y = √(2 * 5*5 * 17)
y = 5 * √34
5 goes in the box.
Find the area of the triangle
A
47°
b
32 ft
C
19 ft
Answers
Answer:
222 [ft²].
Step-by-step explanation:
1. the required area can be calculated according to the formula:
A=0.5*b*c*sin(A);
2. after substitution of b=32; c=19 and sin(A)≈0.7313537:
A=0.5*32*19*0.7313537=222.3315248 [ft²].
I dont get this question equation
y=0.5 (6) - 4
I know that 0.5 is equivalent to 1/2 but I just don’t get this question
Answers
To solve the equation, you first need to simplify 0.5(6) to get 3, since 0.5 is equivalent to 1/2 and multiplying 6 by 1/2 gives you 3. So the equation becomes:
y = 3 - 4
Next, you need to subtract 4 from 3 to get -1. So the solution to the equation is:
y = -1
Therefore, when the value of the independent variable is 6, the value of the dependent variable is -1.
Answer
\(\pink\sf{y=-1}\)
Step-by-step explanation
I'm assuming that this exercise is asking us to simplify the equation \(\sf{y=0.5(6)-4}\).
We know that 0.5 (6) means 0.5 multiplied by 6. That is the same as 6 divided by 2, which is 3:
\(\sf{y=3-4}\)
And now we just simplify the last part:
\(\sf{y=-1}\)
∴ answer: y = -1
Certain advertisers would like to estimate the proportion of viewers who spend the majority of their television time
watching alone. The consensus is that this percentage has been increasing over the years due to the increased
number of television sets in households.
a. Determine the sample size needed to construct a 90% confidence interval with a margin of error of no more than
6% to estimate the true proportion of viewers who watch television alone.
b. What impact would a pilot sample that showed that 44% of viewers spend the majority of their television time
watching alone have on your on results.
a. The sample size needed is
(Round up to the nearest integer.)
b. The new sample size needed would be 0
(Round up to the nearest integer.)
Answers
Answer:
Step-by-step explanation:

You are given the following information about y and x.
y Dependent Variable x Independent Variable
70 2
65 4
78 5
95 6
The least squares estimate of b1 equals:_____
a. 5.83
b. -4.27
c. 11.24
Answers
Answer:
b0 = 5.83
b1 = 52.23
Step-by-step explanation:
Given the data:
X:
2
4
5
6
Y
70
65
78
95
General form of a linear regression equation :
y = b1x + b0
b1 = slope ; b0 = intercept
Using an online regression calculator, the regression equation obtained is :
y = 5.8286 + 52.2286x
Comparing the equation ;
b1 = 52.23
b0 = 5.83