What is the equation of the line that passes through the point (8,6)
and has a slope of frac{1}{4}
Answers
\((\stackrel{x_1}{8}~,~\stackrel{y_1}{6})\hspace{10em} \stackrel{slope}{m} ~=~ \cfrac{1}{4} \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{6}=\stackrel{m}{ \cfrac{1}{4}}(x-\stackrel{x_1}{8}) \\\\\\ y-6=\cfrac{1}{4}x-2\implies y=\cfrac{1}{4}x+4\)
Related Questions
how many weeks of data must be randomly sampled to estimate the mean weekly sales of a new line of athletic footwear? we want 90 % confidence that the sample mean is within $400 of the population mean, and the population standard deviation is known to be $1,200 .
Answers
24 weeks of data must be randomly sampled to estimate the mean weekly sales.
The data is ∝=0.10
\(\sigma=\$ 1200, E=\$ 400$\)
The margin of error is given by this formula:
\($$M E=z_{\alpha / 2} \frac{\sigma}{\sqrt{n}}$$\)
And on this case we have that ME =400 and we are interested in order to find the value of n, if we solve n from equation.
\($$\begin{aligned}n & =\left(z_\alpha\right)^2 \times\left(\frac{\sigma}{E}\right)^2 . \\& =(1.645)^2 \times\left(\frac{1200}{400}\right)^2 \\& =2.706025 \times \frac{1440000}{160000} \\& =24.354225 \approx 24 \\n & =24 \\\end{aligned}$$\)
There are 24 weeks of data must be randomly sampled to estimate the mean weekly sales of a new line of athletic footwear.
For such more questions about randomly
https://brainly.com/question/14561295
#SPJ4
This graph shows all the key characteristics of a particular polynomial function. Drag tiles to complete the function rule that could be represented by the graph

Answers
The function rule that could be represented by the graph is given as follows:
y = 2x³ + x - 3.
How to define the function?The first step in defining the function is looking at it's y-intercept, which is the value of y when the graph of the function crosses the y-axis.
This value is of -3, hence the function can be defined as follows:
f(x) = ax^n + x - 3.
Then we look at the behavior of the function. It has an inflection point, as it is concave down and then it becomes concave up, hence:
It's second derivative is of the first degree.It's first derivative is of the second degree.The function is of the third degree, hence n = 3.Thus:
f(x) = ax³ + x - 3.
Then we look at the x-intercept, meaning that when x = 1, y = 0, this the leading coefficient is obtained as follows:
0 = a + 1 - 3
a = 2.
Thus the function is defined as follows:
y = 2x³ + x - 3.
More can be learned about functions at https://brainly.com/question/24808124
#SPJ1
A clothing designer determines that the number of shirts she can sell is given by the formula S = −4x2 + 80x − 76, where x is the price of the shirts in dollars. At what price will the designer sell the maximum number of shirts? a $324 b $19 c $10 d $1
Answers
To find the price at which the designer will sell the maximum number of shirts, we need to determine the vertex of the quadratic function representing the number of shirts sold.
The equation for the number of shirts sold is given by:
S = -4x^2 + 80x - 76
This is a quadratic function in the form of:
S = ax^2 + bx + c
To find the price at which the maximum number of shirts is sold, we need to locate the vertex of the quadratic function. The x-coordinate of the vertex can be found using the formula:
x = -b / (2a)
In this case, a = -4 and b = 80. Plugging in these values, we can calculate the x-coordinate:
x = -80 / (2*(-4))
x = -80 / (-8)
x = 10
Therefore, the designer will sell the maximum number of shirts at a price of $10. Hence, the correct option is c) $10.
Multiplying Polynomials.
Simplify each difference.
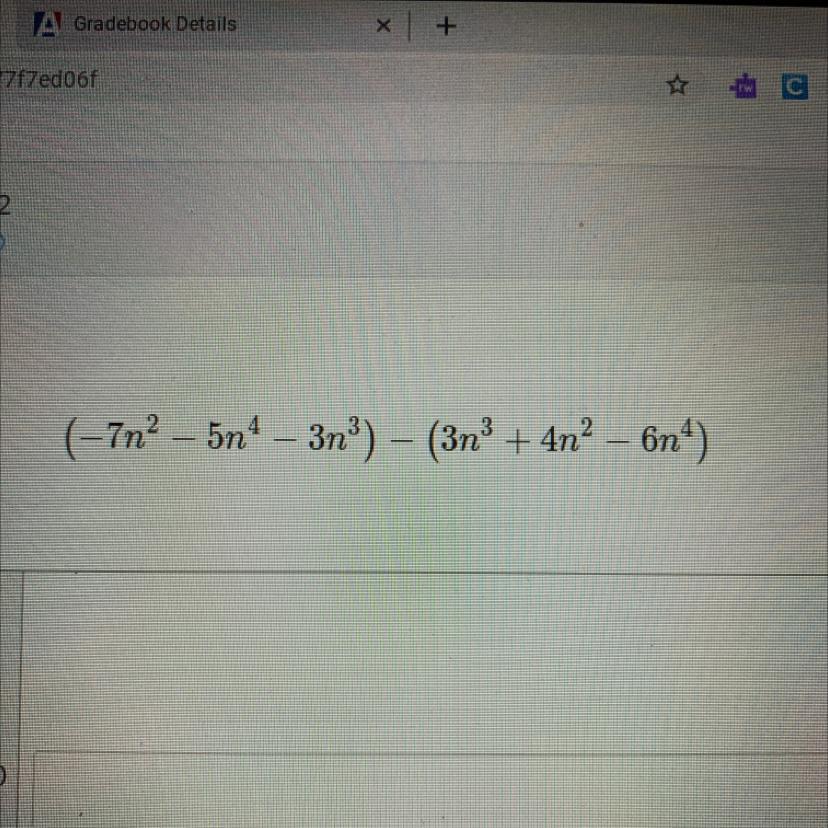
Answers
-11n^2+n^4-6n^3
Answer is n^4-6n^3-11n^2
Solve the proportion for x

Answers
\( \frac{45}{40} = \frac{9}{x} \\ = > \frac{40}{45} = \frac{x}{9} \\ = > x = \frac{40}{45} \times 9 \\ = > x = \frac{40}{5} \\ = > x = 8\)
Answer:x = 8
use the method of variation of parameters to solve the initial value problem x' = ax f(t), x(a) = xa using the following values. 4 -2 16t2 0 1 2t - 40 a= f(t) = x(0) = 2 - 1 4t t 1-2t x(t) =
Answers
The process involves finding the complementary solution x_c(t) by solving the homogeneous equation, determining the particular solution x_p(t) using the method of variation of parameters, and combining them to obtain the general solution x(t).
1. The method of variation of parameters can be used to solve the initial value problem x' = axf(t), x(a) = xa, where a and f(t) are given functions. In this case, we have the values a = 4 - 2t and f(t) = 16t^2. We need to find the solution x(t) using the initial condition x(0) = 2.
2. To solve the initial value problem using the method of variation of parameters, we first find the complementary solution x_c(t) by solving the homogeneous equation x' = ax.
3. For the given a = 4 - 2t, the homogeneous equation becomes x' = (4 - 2t)x. By separation of variables and integration, we find the complementary solution x_c(t) = Ce^(2t - t^2).
4. Next, we find the particular solution x_p(t) by assuming a particular solution of the form x_p(t) = u(t)e^(2t - t^2), where u(t) is a function to be determined.
5. Differentiating x_p(t) and substituting it into the original differential equation, we can solve for u'(t) and determine the form of u(t). After finding u(t), we substitute it back into x_p(t).
6. Finally, the general solution is given by x(t) = x_c(t) + x_p(t). By substituting the values and integrating, we can obtain the specific solution x(t) for the given initial condition.
Learn more about homogeneous equation here: brainly.com/question/12884496
#SPJ11
there 3 cups of ketchup for every 1/2 cup of mustard what is the rate in cups of per ketchup per mustard
Answers
There are 3 cups of ketchup for every 1/2 cup of mustard, then the rate in cups of ketchup per cup of mustard is:
3÷1/2 = 3*2 = 6 cups of ketchup per cup of mustard
If a family has five girls and plans to have another child, answer the following if the probability of the event of a boy being born is \( \frac{1}{2} \), and births are independent events. a. What is
Answers
In a family with five girls and the probability of a boy being born is 1/2, the probability of the next child being a boy is still 1/2.
The previous births do not affect the probability of the next birth since each birth is an independent event.
The probability of an event occurring is determined by the ratio of the number of favorable outcomes to the total number of possible outcomes. In this case, the event of interest is the birth of a boy.
Since each birth is an independent event, the probability of having a boy on any given birth is always 1/2, regardless of the previous children born.
In the given scenario, the family already has five girls. This information is not relevant to the probability of the next child being a boy. The gender of the previous children does not affect the probability of the next child being a boy or a girl.
Therefore, the probability of the next child being a boy remains 1/2, as it is for any independent birth event.
To learn more about independent event visit:
brainly.com/question/32716243
#SPJ11
did we prove the conclusion true for every isosceles triangle or only for this specific isosceles triangle?
Answers
∠A = ∠C for every isosceles triangle and not only for this specific isosceles triangle.
We are given that:
AB = BC
Now, draw a angle bisector from point B to the line AC in a way that it intersects AC at D.
Now, we get that:
∠ABD = ∠CBD ( BD is the angle bisector)
BD = BD ( common line)
So, ΔABD ≅ Δ CBD ( SAS property)
So,
∠A = ∠ C ( CPCT rule)
Also, it will be true for every isosceles triangle.
Therefore, we get that, ∠A = ∠C for every isosceles triangle and not only for this specific isosceles triangle.
Learn more about triangles here:
https://brainly.com/question/17335144
#SPJ4
Your question was incomplete. Please refer the content below:
There is an isosceles triangle with AB = BC. Prove that ∠A = ∠C.
Did we prove the conclusion true for every isosceles triangle or only for this specific isosceles triangle.

Without actually solving the given differential equation, find the minimum radius of convergence R of power series solutions about the ordinary point x = 0. About the ordinary point x = 1. (x^2 - 2x + 10)y" + xy' - 4y =
Answers
Here, to find the minimum radius of convergence R of power series solutions about the ordinary point x = 0 and x = 1, for the differential equation (x^2 - 2x + 10)y" + xy' - 4y = 0, we can use the formula R = 1/limsup |an|^1/n.
Step:1 At x = 0, the power series solution is y = c_0 + c_1x + c_2x^2 + c_3x^3 + ... + c_nx^n + ... , and the coefficients an are given by c_n = (-1)^(n-1)*(n-1)!/[(x^2-2x+10)n!]. Thus, the minimum radius of convergence R at x = 0 is R = 1/limsup |c_n|^1/n.
Step:2 Similarly, at x = 1, the power series solution is y = c_0 + c_1(x-1) + c_2(x-1)^2 + c_3(x-1)^3 + ... + c_n(x-1)^n + ..., and the coefficients an are given by c_n = (-1)^(n-1)*(n-1)!/[((x-1)^2-2(x-1)+10)n!]. Thus, the minimum radius of convergence R at x = 1 is R = 1/limsup |c_n|^1/n.
Learn more about power series here, https://brainly.com/question/28209832
#SPJ11
I believe this is pretty easy but it's: solve for x using common denominators 3/4(x+2)=x/(x+3) Answer choices below:

Answers
Answer:
x = \(\frac{3}{4}\)
Step-by-step explanation:
Given
\(\frac{3}{4(x+2)}\) = \(\frac{x}{x+2}\)
multiply numerator/ denominator of \(\frac{x}{x+2}\) by 4, thus
\(\frac{3}{4(x+2)}\) = \(\frac{4x}{4(x+2)}\)
Since the denominators are common , equate the numerators, that is
4x = 3 ( divide both sides by 4 )
x = \(\frac{3}{4}\)
Select all that are like radicals after simplifying.
a. √50x^2
b. √32x
c. √18n
d. √72x^2
Answers
A: √50x^2 and d: √72x^2 are like radicals.
Like radicals are square roots with the same coefficient outside the radical. For example, √50x^2 and √72x^2 can be simplified to √2 * √25x^2, which makes them like radicals. Simplifying the expressions helps to see if they are alike.
Expressions such as √32x and √18n cannot be simplified to have the same coefficient outside the radical and hence, they are not like radicals.
In conclusion, only √50x^2 and √72x^2 are like radicals after simplification.
You can learn more about like radicals at
https://brainly.com/question/3253643
#SPJ4
Answer:
A&D
Step-by-step explanation:
Got it right on edge
4/5 = 17/x
Find x please!!
*ratios and proportions*
Answers
Answer:
So, first you need to set up a proportion and cross multiply. This allows you to get an equation which you can solve for x.
Step-by-step explanation:
\(\frac{4}{5}\) × \(\frac{17}{x}\)
Cross multiply to get 4x = 85
Next, isolate the x variable by dividing the 4 on both sides. This leaves you with x = 21.25.
Answer: x = 21.25
What does m∠1 ≅ m∠5 mean?
Answers
Answer:
The symbol ≅ means congruent or approximately equal to. In this case, since we are referring to m∠1 and m∠5, we can decide that this sign means congruent/equal to each other.
If f(x) = 2x + 4, what does f(2) + f(5) =
Answers
Answer:
22
Step-by-step explanation:
f(2) : 2*2 = 4 , 4+4 = 8
f(5) ; 2*5 = 10 ; 10+4 = 14
8+14 = 22
Answer:
f(2) = 8, f(5) = 14.
Step-by-step explanation:
in f(2), 2 will replace x. in f(5), 5 will replace x.
f(2)= 2(2) + 4.
f(2)= 4 + 4.
f(2)= 8
f(5)= 2(5) + 4
f(5)= 10+ 4
f(5)= 14
How do you prove two triangles are similar using SAS?
Answers
Without knowledge of all sides and angles, it is still possible to confirm that two triangles are comparable.
According to the SAS criteria for triangle similarity, two sides of one triangle are comparable to two sides of another triangle if their included angles are congruent.According to the SAS Similarity Theorem, two triangles are similar if their respective sides are proportionate to one another and their included angles are congruent.
Given:
PQ/XY = QR/YZ and ∠Q ≅ ∠Y
To prove that, △PQR is similar to △XYZ.
Proof: Assume PQ > XY
Draw MN parallel to BC, we find that MQN similar to XYZ
QM/QP = QN/QR --- (1)[using the basic proportionality theorem]
Now △MQN and △XYZ are congruent thus, XY/QP = YZ/QR --- (2)
Since QM = XY from (1) and (2),
XY/QP = QM/QP = QN/QR = YZ/QR
Thus, QN = YZ by SAS congruence criterion.
△MQN ≅ △XYZ
But △MQN congruent to △XYZ,
Thus, △PQR is similar to △XYZ.
To know more about angles check the below link:
https://brainly.com/question/25770607
#SPJ4
Consider the function f(x) = -4x²-9x+20.
Determine f(-2)=

Answers
Step-by-step explanation:
you just substitute (-2) into the x values of the above function \(f( - 2) = - 4( - 2)^{2} - 9( - 2) + 20 \\ f( - 2) = 22\)5. 62% of what number is 9.5?
Answers
Answer:15.32258064516
Step-by-step explanation:
15.32258064516
the product of a number and 13 increased by 5 is -12
Answers
Answer:
13x + 5= -12
hope this helps :)
Solve the system of equations.
14x + 5y = 31
2x – 3y = -29
2 =
y =
Answers
Answer:
X,y=83/52 ,45/26
Step-by-step explanation:
just look up your answer and you will find the step by step. Hopefully this helped :)
Determine the no-arbitrage price today of a 5 year $1,000 US
Treasury note with a coupon rate of 2% and a YTM of 4.25% (APR) (to
the penny)
A. $739.65
B. $900.53
C. $819.76
D. $89
Answers
The no-arbitrage price today of a 5-year $1,000 US Treasury note with a 2% coupon rate and a 4.25% yield to maturity is approximately $908.44, closest to option B: $900.53.
To determine the no-arbitrage price of a 5-year $1,000 US Treasury note with a coupon rate of 2% and a yield to maturity (YTM) of 4.25%, we can use the present value of the future cash flows.First, let's calculate the annual coupon payment. The coupon rate is 2% of the face value, so the coupon payment is ($1,000 * 2%) = $20 per year.The yield to maturity of 4.25% is the discount rate we'll use to calculate the present value of the cash flows. Since the coupon payments occur annually, we need to discount them at this rate for five years.
Using the present value formula for an annuity, we can calculate the present value of the coupon payments:PV = C * (1 - (1 + r)^-n) / r,
where PV is the present value, C is the coupon payment, r is the discount rate, and n is the number of periods.
Plugging in the values:PV = $20 * (1 - (1 + 0.0425)^-5) / 0.0425 = $85.6427.
Next, we need to calculate the present value of the face value ($1,000) at the end of 5 years:PV = $1,000 / (1 + 0.0425)^5 = $822.7967.
Finally, we sum up the present values of the coupon payments and the face value:No-arbitrage price = $85.6427 + $822.7967 = $908.4394.
Rounding to the penny, the no-arbitrage price is $908.44, which is closest to option B: $900.53.
To learn more about discount rate click here
brainly.com/question/31318990
#SPJ11
which statistic of the sampling distribution is used in calculating the margin of error for a confidence interval of the population mean?
Answers
Standard Deviation statistic of the sampling distribution is used in calculating the margin of error for a confidence interval of the population mean.
Basically, the margin of error is stated as follows:
Error margin, E = Z* (Standard deviation)
Therefore, the calculation of the margin of error does not employ the mean at all.
The margin of error is computed using the standard deviation.
The term "standard deviation" reveals that a measurement of the data's dispersion from the mean. While a high standard deviation indicates that the data are more spread or dispersed, a low standard deviation suggests that the data are clustered or gathered around the mean.
It depicts the average deviation of each score from the mean. A high standard deviation in a normal distribution denotes that values are often far from the mean, while a low standard deviation denotes that values are grouped together around the mean.
To know more about 'Standard Deviation' related questions
visit- https://brainly.com/question/13905583
#SPJ4
Which graph represents the equation y equals one half times x minus 1?
graph of a line passing through the points negative 2 comma negative 2 and 0 comma negative 1
graph of a line passing through the points negative 2 comma 0 and 0 comma 1
graph of a line passing through the points negative 2 comma negative 3 and 0 comma negative 2
graph of a line passing through the points negative 4 comma 0 and 0 comma 2
Answers
The correct graph which represents the equation y = 1/2x - 1 is,
⇒ Graph of a line passing through the points negative 2 comma negative 2 and 0 comma negative 1.
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
The equation is,
⇒ y = 1/2x - 1
Now, After draw the equation we get;
Graph of a line passing through the points (-2, - 2) and (0, - 1).
Thus, The correct statement is,
⇒ Graph of a line passing through the points negative 2 comma negative 2 and 0 comma negative 1.
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1

Someone please help me solve this. I’ve tried solving it l but my answer is always wrong

Answers
Answer:
I think it is 636 pounds
Step-by-step explanation:
if I'm right plz give me brainliest
Can anyone solve for y? Thanks!

Answers
Step-by-step explanation:
(4y-6) and 14 are vertical angles this they are equal
\(4y - 6 = 14\)
\(4y = 20\)
\(y = 5\)
Likewise, 5x-5 and 3x+17 are equal
\(5x - 5 = 3x + 17\)
\(2x = 22\)
\(x = 11\)
Please note that the degree measure is not 11 itself, that the value of the x variable,
In fact, if you plug in 11 for x.
The value of the variable will be
50 degrees
A small software development company invests $16,000 to produce a software package that will sell for $50.65. Each unit costs $8.20 to produce. How many units must the company sell to break even? How many units must the company sell to make a profit of $95,000?
Answers
Answer:
376 units and 1,857 units
Step-by-step explanation:
The computation is shown below:
The number of units that company sells to break even is
Let us assume the number of units be x
$16,000 + $8.20x = $50.75x
$16,000 = $50.75x - $8.20x
$16,000 = $42.55
x = $16,000 ÷ $42.55
= 376 units
Now in order to make the profit the number of units sold is
$50.65x - ($16,000 + $8.20x) = $95,000
$50.65x - $16,000 - $8.20x = $95,000
$42.55x = $95,000 - $16,000
$42.55x = $79,000
x = $79,000 ÷ $42.55
= 1,857 units
There are 125 people in a sport centre.
59 people use the gym.
70 people use the swimming pool.
55 people use the track.
25 people use the gym and the pool.
30 people use the pool and the track.
17 people use the gym and the track.
6 people use all three facilities.
A person is selected at random.
What is the probability that this person doesn't use any facility?
Answers
Probability that the person selected at random from the sport centre of 125 people is a fraction of 1/4 or 0.25.
Probability of an eventThe probability of an event is the fraction of the required number of outcome divided by the number of possible outcomes.
We shall determine the answer to the question as follows;
People in the sport centre = 125
People who used the 3 facilities = 6
People who accessed only gym = 59 - (6 + 11 + 19) = 26
People who accessed only track event = 55 - (6 + 11 + 24) = 14
People who accessed only swimming pool event = 70 - (6 + 19 + 24) = 21
People who accessed only gym and swimming pool events = 29 - 6 = 19
People who accessed only gym and track events = 17 - 6 = 11
People who accessed only swimming pool and track events = 30 - 6 = 24
Total number of people who accessed at least any one of the facilities = 121
The number of people who did not access any of the facility = 125 - 121 = 4, which is the number of possible outcomes for our required outcome.
Therefore, the probability that the person selected doesn't use any facility = 1/4
Learn more about probability here: https://brainly.com/question/25870256
#SPJ1
The length of a rectangle is 3 yd longer than its width. if the perimeter of the rectangle is 58 yd, find its length and width.
Answers
Answer:
Length = 16 yds
Width = 13 yds
Step-by-step explanation:
P = 2w + 2l
l = w + 3
58 = (2w + 2(w + 3))
58 = 4w + 6
52 = 4w
w = 13
L = w + 3
= 13 + 3
= 16
The length and width of the rectangle are 16,13yd.
The Length and Width of the rectangle can be found as:
Given:The length of the rectangle is 3yds longer than the width which means length = w+3
and the perimeter is given by 58yd
Let W be the width and L be the length
We know that the perimeter of a rectangle is 2(L+w)
The perimeter of a rectangle is defined as the sum of all the sides of a rectangle
By simplifying we get2(w+w+3)=58
2(2w+3)=58
2w=29-3
w=13
then the length of the rectangle will be w+3
13+3 = 16
Learn more about the length, width, and perimeter of a rectangle here:
https://brainly.com/question/7245786
#SPJ4
Matilda has 16 3/4 hours to finish three consulting projects.how much time may she spend on each project ,if she plans to spend the same amount of time on each?
Answers
Time taken by Matilda on each project is \(5\frac{7}{12}\) hours.
According to the question we have been given that,
Total time taken by Matilda to complete the consulting projects = \(16\frac{3}{4}\) hours
First we will convert it into simple fraction which is
\(16\frac{3}{4} = \frac{67}{4} \\\) hours
Number of consulting projects = 3
And Matilda spends same amount of time to each of the project.
To find the time she spend on each project is by using unitary method
that is, 3 projects = \(\frac{67}{4}\) hours
1 project = \(\frac{67}{4} / 3\)
= 67/12
= \(5\frac{7}{12}\) hours
Hence time taken by Matilda on each project is \(5\frac{7}{12}\) hours.
Learn more about unitary method here : https://brainly.com/question/24587372
#SPJ4
Help please no link bots allowed

Answers
Answer:
it's D
Step-by-step explanation:
D is the angle (answer)