What is the following simplified product? Assume x≥0.
(√10xX* -x√5x²][2√15x* + √√3x³)
O 10x4 √6+x3√30x-10x4√3+x²15x
O 10x4 √√6+x3√30x-x√75+x²15
10x4 6+x3√30x-10x4√3-x²15
O 10x4 √√6+x3 30x-10x4√3-x³15x
Answers
The simplified product of (√10xX* -x√5x²)(2√15x* + √√3x³) is O 10x4 √6+x3√30x-10x4√3-x²15.
To simplify the given product, we can use the distributive property and combine like terms. First, we multiply the terms inside the brackets:
√10xX* * 2√15x* = 2√10xX* * √15x* = 2√(10 * 15)xX* * x* = 2√150x²X* * x* = 2x²√150X* * x* = 2x³√150X.
Next, we multiply the remaining terms:
-x√5x² * 2√15x* = -2x²√5x² * √15x* = -2x²√(5 * 15)x² * x* = -2x⁴√75x² * x* = -2x⁵√75x.
Combining the multiplied terms, we have:
2x³√150X - 2x⁵√75x.
Finally, we can simplify further by factoring out common terms:
2x³√(150X - 75x).
Simplifying 150X - 75x, we get:
150X - 75x = 75(2X - x) = 75x.
Therefore, the simplified product is:
2x³√75x.
Note: The option "10x4 √6+x3√30x-10x4√3-x²15" mentioned in the answer may contain a typographical error since the exponent notation (10x4) is unclear. The correct notation should be 10x^4, where '^' represents exponentiation.
for such more questions on product
https://brainly.com/question/28782029
#SPJ8
Related Questions
The height of a pyramid in Egypt is 150m and has a square base with a side 220m,then it's volume is
Answers
Answer:
2,420,000 m³
Step-by-step explanation:
You want the volume of a square pyramid 220 m on a side and 150 m high.
VolumeThe volume of a pyramid is 1/3 the volume of a cuboid of the same dimensions.
V = 1/3LWH
V = 1/3(220 m)²(150 m) = 2420000 m³
The volume of the pyramid is about 2,420,000 cubic meters.
__
Additional comment
The density of Egyptian limestone is between 2.4 and 2.7 g/cm³, so the mass of the pyramid is approximately 6 million metric tons. This is about 50% more than the most massive building built in modern times.
View Policies Current Attempt in Progress Using the information provided in the table, the network diagram and the project completion time = 25 weeks, reduce the completion time of the project by 5 we
Answers
Strategies such as fast-tracking, crashing, prioritization, and resource optimization can be employed to reduce the project completion time by 5 weeks.
To reduce the completion time of the project by 5 weeks, we need to analyze the provided information and make appropriate adjustments. The initial completion time of the project is 25 weeks.
To achieve a reduction of 5 weeks, we can consider several strategies:
1. Fast-tracking: This involves overlapping or parallelizing certain project activities that were initially planned to be executed sequentially. By identifying tasks that can be performed concurrently, we can potentially save time. However, it's important to evaluate the impact on resource allocation and potential risks associated with fast-tracking.
2. Crashing: This strategy focuses on expediting critical activities by adding more resources or adopting alternative approaches to complete them faster. By compressing the schedule of critical tasks, we can reduce the overall project duration. However, this may come at an additional cost.
3. Prioritization: By reevaluating the project tasks and their priorities, we can allocate resources more efficiently. This ensures that critical activities receive higher attention and are completed earlier, resulting in an accelerated project timeline.
4. Resource optimization: Analyzing the resource allocation and identifying potential areas for optimization can lead to time savings. By ensuring that resources are utilized effectively and efficiently, we can streamline the project execution process.
It's important to note that implementing any of these strategies requires careful evaluation, considering factors such as project constraints, risks, cost implications, and stakeholder agreements. A comprehensive analysis of the project plan, resource availability, and critical path can guide the decision-making process for reducing the project completion time.
To know more about project management techniques and strategies, refer here:
https://brainly.com/question/32653641#
#SPJ11
if the value stated by a null hypothesis is ______ the confidence interval, then the decision would have likely been to retain the null hypothesis.
Answers
If the value stated by a null hypothesis is within the confidence interval, then the decision would have likely been to retain the null hypothesis.
In hypothesis testing, the null hypothesis represents the default assumption or the claim that there is no significant difference or relationship between variables. The confidence interval, on the other hand, provides a range of plausible values for the population parameter based on sample data. If the value stated by the null hypothesis falls within the confidence interval, it means that the null hypothesis value is considered plausible or consistent with the observed data.
In this case, there is insufficient evidence to reject the null hypothesis, and the decision would be to retain it. On the other hand, if the null hypothesis value is outside the confidence interval, it suggests that the null hypothesis is unlikely, and the decision would be to reject it in favor of an alternative hypothesis.
To learn more about null hypothesis click here: brainly.com/question/30821298
#SPJ11
square root 2x-7 = 1
Answers
Answer:
4
Step-by-step explanation:
To solve for x in the equation:
√(2x - 7) = 1
We can start by isolating the square root by squaring both sides of the equation:
(√(2x - 7))^2 = 1^2
2x - 7 = 1
Next, we can isolate the variable by adding 7 to both sides of the equation:
2x = 8
Finally, we can solve for x by dividing both sides by 2:
x = 4
Therefore, the solution to the equation √(2x - 7) = 1 is x = 4.
Help appreciated, thanks so much!

Answers
Answer:
r= -6
Step-by-step explanation:
Solve by completing the square : x^2+4x-7=0 and 2x^2+8x-1=0


Answers
By completing the squares we will see that the solutions are:
a) For 2x^2 + 8x - 1 = 0:
x = -2 ±√4.5
b) For x^2+4x-7 = 0
x = ±√11 - 2
How to complete squares?Remember that the perfect square trinomial is:
(a + b)^2 = a^2 + 2ab + b^2
The first quadratic equation is:
2x^2 + 8x - 1 = 0
Dividing by 2 we get:
x^2 + 4x - 1/2 = 0
We can rewrite this as:
x^2 + 2*2*x - 1/2 = 0
Adding and subtracting 2^2 = 4, we get:
x^2 + 2*2*x + 4 - 4 - 1/2 = 0
(x + 2)^2 - 4 - 1/2 = 0
(x + 2)^2 = 4.5
Now we can solve this:
x + 2 = ±√4.5
x = -2 ±√4.5
These are the two solutions.
The other quadratic equation is:
x^2+4x-7 = 0
We can rewrite this as:
x^2 + 2*2*x - 7 = 0
Again, add and subtract 4 to get:
x^2 + 2*2*x + 4 - 4 - 7 = 0
(x + 2)^2 = 11
Solving this we get:
x = ±√11 - 2
Learn more about quadratic equations:
https://brainly.com/question/1214333
#SPJ1
If an 82 ft flag pole casts a shadow 45 ft. Long, the angle of elevation of the sun is.
Answers
Given that an 82 ft flag pole casts a shadow 45 ft long.
In the above diagram, AB is the flag, BC is the shadow and angle C is the ngle of elevation.
Now,
\(\begin{gathered} \tan c=\frac{82}{45} \\ c=\tan ^{-1}(\frac{82}{45}) \\ =61.243 \end{gathered}\)So, teh angle of elevation is 61.243 degrees.

the manager of a local stadium is interested in how many fans purchase peanuts at events. in a random sample of ,200 fans chosen from several different events, 94 of them purchased peanuts. what does this data imply about the claim that half of the people who attend events purchase peanuts?
Answers
According to the given data 47% of the fans that attend the event, purchase the peanuts.
The sample collected was among 200 fans which means total fans = 200
out of which 94 fans purchased peanuts which means
Percentage of Fans purchased Peanuts = \(\frac{94}{200}\) X 100
= 47 %
Not exactly the half of the fans purchased the peanuts but approximately half that is 3% less than 50 % fans puchased the peanuts which implies => 47 % fans purchased peanuts.
#SPJ4
hii please help asap ill give brainliest thanks

Answers
Answer:
C
Step-by-step explanation:
The teachings of Buddha
demonstrate that the equation 3x 17 1111 = 27y 15z has no solution in which x, y, and z are integers.
Answers
Since 3x¹⁷ + 1111 is not equivalent to 27y + 15z. So, there does not exist any solution.
We have to demonstrate that the equation 3x¹⁷ + 1111 = 27y + 15z has no solution in which x, y, and z are integer.
Equations with no solution have no values of x that make the equation true.
The equation 3x¹⁷ +1111 = 27y +15z
Since, x, y and z are integers.
Therefore, 27y + 15z ≅ 0(mod3).
But, 3x¹⁷ + 1111 ≅ 1(mod3).
Hence, 3x¹⁷ + 1111 is not equivalent to 27y + 15z.
Thus, there is no existing solution.
To learn more about types of solution link is here
brainly.com/question/30239692
#SPJ4
The complete question is:
Demonstrate that the equation 3x¹⁷ +1111 = 27y +15z has no solution in which x, y, and z are integer.
Sin A 4/5.
Find
COSA + tan A
Answers
Answer:
Step-by-step explanation:
The opposite side (the one not connected to A) = 4
The hypotenuse is 5
The adjacent side needs to be found for the cosine and the tangent.
a^2 + b^2 = c^2
a = opposite side = 4
b = adjacent side = ?
c = hypotenuse = 5
4^2 + x^2 = 5^2
16 + x^2 = 25
x^2 = 25 - 16
x^2 = 9
x = sqrt(9)
x = 3
cos(A) = adjacent / hypotenuse = 3/5
Tan(A) = opposite / adjacent = 4/3
cos(A) + tan(A) = 3/5 + 4/3
cos(A) + tan(A) = 9/15 + 20/15 = 29/15
To find: CosA + TanA
Solution:
16/25 + Cos²A = 1 [Sin²A + Cos²A = 1]
Cos²A = 1 - 16/25
Cos²A = 25 - 16/25
Cos²A = 9/25
CosA = 3/5
We know that TanA = SinA/CosA
TanA = (4/5)/(3/5)
TanA = 4/3
CosA + TanA = 3/5 + 4/3 = 29/15
permudahkan. 1. 3/4m (4m+16n) +m/n.
Answers
3/4m(4m+16n) + m/n open the bracket of equation,
3/4m(4m+16n) + m/n = 3+ 12n/m + m/n
now multiply and devide by mn on RHS,
3/4m(4m+16n) + m/n = (3mn+12n²+m²)/mn
College Algebra Applied Problem Four A medical professional is helping an individual balance their diet. The individual has asked for some certain foods to remain in their diet. They will always get 600 calories from carbohydrates. The individual says that they can be flexible about how many calories they consume in fats and proteins. The goal of the diet is to keep the individual at 1,800 calories per day ( 600 of which come from carbohydrates). Part One Write an equation that models the amount of calories from fats " f ' and protein "p" that the individual can consume in order to reach 1,800 calories. Part Two The diet being prescribed to the individual calls for calories from protein to be three times the calories from fat. Write an equation based on this information that relates calories from protein "p" to calories from fat " f ". Part Three Use your equations from parts "b" and "c" to solve this system of equations and determine the amount of calories that the individual should consume from fats and proteins. Part Four If the individual no longer required 600 calories from carbohydrates, and instead said that they would be flexible about how many carbohydrates they would consume, how many variables would there be for this problem on calories?
Answers
The system equation that models the amount of calories from fats (f) and proteins (p) that the individual can consume to reach 1,800 calories is: f + p = 1,200. The equation that relates calories from protein (p) to calories from fat (f) based on the prescribed diet is: p = 3f. Solving the system of equations, we find that the individual should consume 300 calories from fats and 900 calories from proteins.
To find the equation that models the amount of calories from fats and proteins that the individual can consume in order to reach 1,800 calories, we consider that 600 calories will come from carbohydrates. Since the total goal is 1,800 calories, the remaining calories from fats and proteins should add up to 1,800 - 600 = 1,200 calories. Therefore, the equation is f + p = 1,200.
Based on the prescribed diet, the individual is required to consume calories from protein that are three times the calories from fat. This relationship can be expressed as p = 3f, where p represents the calories from protein and f represents the calories from fat.
To solve the system of equations, we substitute the value of p from the second equation into the first equation: f + 3f = 1,200. Combining like terms, we get 4f = 1,200, and dividing both sides by 4 yields f = 300. Substituting this value back into the second equation, we find p = 3(300) = 900.
Therefore, the individual should consume 300 calories from fats and 900 calories from proteins to meet the diet requirements and achieve a total of 1,800 calories.
Learn more about system equation
brainly.com/question/32645146
#SPJ11
the students of 3 sections of a class have to stand in rows each row has an equal number of students if there are 24 , 36 , and 60 students in 3 sections find the maximum number of students in each row
Answers
The maximum Number of scholars in each row is 12. This means that the scholars can be arranged in rows with an equal number of scholars, and each row can have a outside of 12 scholars.
To find the maximum number of scholars in each row, we need to determine the topmost common divisor( GCD) of the total number of scholars in each section. The GCD represents the largest number that divides all the given figures unevenly.
Given that there are 24, 36, and 60 scholars in the three sections, we can calculate the GCD as follows Step 1 List the high factors of each number 24 = 23 * 31 36 = 22 * 32 60 = 22 * 31 * 51
Step 2 Identify the common high factors among the three figures Common high factors 22 * 31 Step 3 Multiply the common high factors to find the GCD GCD = 22 * 31 = 4 * 3 = 12
thus, the maximum number of scholars in each row is 12. This means that the scholars can be arranged in rows with an equal number of scholars, and each row can have a outside of 12 scholars.
For more questions on Number .
https://brainly.com/question/26460978
#SPJ8
separate the coefficient from the variable in each expression and write the variable with a negative exponent if it was originally in the denominator.
Answers
The result of the given expression is-
\(2^3\left(x-\frac{3}{2}\right)^6\)
What is exponents?The amount of times a quantity is multiplied is referred to as its exponent. Power is defined as a number multiplied by itself a certain number of times.
The number that a number is raised in order to define its power as an entire expression is known as its exponent.
Now, consider the following exponent rule;
\((x y)^m=x^m y^n, x^{m+n}=x^m x^n, \text { and } \frac{1}{x^n}=x^{-n}\)
Now, according to the question, the given expression is;
\(\frac{(2 x-3)^6}{8}\)
Taking 2 common from the numerator;
\(\frac{\left[2\left(x-\frac{3}{2}\right)\right]^6}{8}\)
Now, apply the given exponent rule \((a b)^m=a^m b^m\) in the above equation.
\(\frac{\left[2\left(x-\frac{3}{2}\right)\right]^6}{8}=\frac{2^6\left(x-\frac{3}{2}\right)^6}{8}\)
Apply \(a^{m+n}=a^m a^n\) in the above result.
\(\begin{aligned}\frac{2^6\left(x-\frac{3}{2}\right)^6}{8} &=\frac{2^{(3+3)}\left(x-\frac{3}{2}\right)^6}{8} \\&=\frac{2^3 \cdot 2^3\left(x-\frac{3}{2}\right)^6}{8} \\&=\frac{8 \cdot 2^3\left(x-\frac{3}{2}\right)^6}{8} \\&=2^3\left(x-\frac{3}{2}\right)^6\end{aligned}\)
Therefore, the simplified form of the given expression is \(2^3\left(x-\frac{3}{2}\right)^6\).
To know more about the exponent rule, here
https://brainly.com/question/11975096
#SPJ4
-
The complete question is-
Separate the coefficient from the variable in each expression and write the variable with a negative exponent if it was originally in the denominator.
\(\frac{(2 x-3)^6}{8}\)
How do you make 70 / 5 equal groups
Answers
Answer:
14
Step-by-step explanation:
divide 70 into 5
if you were to draw it out it would be 5 circles and you put one line until you reach 70 in each circle you would get 14
While a junior in high school, Javier accepted a job stocking shelves at a local grocery
store. He makes an hourly wage of $8.50. He is paid semimonthly and works an
average of 20 hours per week.
What is Javier's monthly income?
$1,473.33
$680
$2,040.00
$736.67
Answers
Answer:
he works 20 per week, so in a month, he will have 20*4= 80 hours, here 4 is the number of weeks in one month, and we have as information that he is paid for one hour $8.50, so you can do: 80*($8.50)= $680
Step-by-step explanation:
(20hours)*(4 weeks)= 80hours
(80hours)*($8.50)= $680
By identifying the vertical asymptote, one can determine the denominator of this
function is

Answers
The denominator of function is -x/2 - 1 and vertical asymptote x = -2.
What is vertical asymptote?A vertical line that is not a part of the function's graph but serves as a guide is known as a vertical asymptote. Because it occurs at an x-value outside of the function's domain, the graph cannot cross it. There may be more than one vertical asymptote for a function.
Given graph
the function of graph is F(x) = \(2\frac{\left(-\frac{x}{2}\ +\ 1\right)}{\left(\frac{x^{2\ }}{4}-1\right)}\) = 2(1- x/2)/(x²/4 - 1)
reducing the equation
F(x) = 2/(-x/2 - 1)
denominator is -x/2 - 1
for vertical asymptote -x/2 - 1 = 0
x = -2
Therefore for function is -x/2 - 1 and vertical asymptote at x = -2.
Learn more about vertical asymptote;
https://brainly.com/question/4084552
#SPJ1
Compute the directional derivative of the following function at the given point Pin the direction of the given vector. Be sure to use a unit vector for the direction vector.f(x,y)=ln(5+3x2+2y2); P(2,−1); ⟨1,1⟩
Answers
The directional derivative of the function at the given point P in the direction of the given vector is:
(8/21)√(2).
Directional derivativeThe directional derivative of a function in the direction of a unit vector is the rate at which the function changes in that direction.
To compute the directional derivative of f(x, y) = ln(5 + 3x^2 + 2y^2) at the point P(2, -1) in the direction of the vector ⟨1, 1⟩, we need to:
Compute the gradient of f(x, y) at P(2, -1).Normalize the direction vector ⟨1, 1⟩ to obtain a unit vector.Compute the dot product of the gradient of f at P with the unit direction vector.The gradient of f(x, y) is given by:1) ∇f(x, y) = (6x / (5 + 3x^2 + 2y^2), 4y / (5 + 3x^2 + 2y^2))
Therefore, the gradient of f at P(2, -1) is:
∇f(2, -1) = (24/21, -4/21)
2) To obtain a unit vector in the direction of ⟨1, 1⟩, we need to divide it by its length:
||⟨1, 1⟩|| = √(1^2 + 1^2) = sqrt(2)
Therefore, a unit vector in the direction of ⟨1, 1⟩ is given by:
u = ⟨1, 1⟩ / √2) = ⟨√(2)/2, √(2)/2⟩
3) The directional derivative of f at P in the direction of u is given by:
D_uf(2, -1) = ∇f(2, -1) · u
where "·" denotes the dot product. Substituting the values for ∇f(2, -1) and u, we get:
D_uf(2, -1) = (24/21, -4/21) · (√(2)/2, √(2)/2)
= (24/21)(√(2)/2) + (-4/21)(√(2)/2)
= (8/21)√(2)
Therefore, the directional derivative of f(x, y) at P(2, -1) in the direction of ⟨1, 1⟩ is (8/21)√(2).
To know more about the "directional derivative": https://brainly.com/question/12873145
#SPJ11
how do you graph parametric equation on desmos?
Answers
Answer:
yes, you can graph parametric equations there. (It's called Desmos, by the way, not “Demos.”) Click on the triple-bar symbol at the top left, which takes you to a drop-down menu. Scroll down that menu until you see the entries for parametric equations. Hope this helps!
Step-by-step explanation:
pls say thx
What is the probability of tossing an odd number with 6 sided number cube ?
Answers
Okay, here we have this:
Considering the provided information, we are going to calculate the requested probability, so we obtain the following:
Let us remember that in a 6-sided dice, the numbers it contains are (1,2,3,4,5,6), and of those 3 are odd, then we are going to substitute in the following formula of the simple probability of an event :
Probability of an event=Favorable Cases/Possible Cases
Probability of tossing an odd number with 6 sided number cube =3/6
Probability of tossing an odd number with 6 sided number cube =1/2
Finally we obtain that the probability of tossing an odd number with 6 sided number cube is 1/2.
Sam made a 70% on his test. If there were 80 questions on the test, how many did he get right?
Answers
Answer: He got 56 questions right.
Step-by-step explanation:
Answer:
Sam got 56 questions correct.
Step-by-step explanation:
If there were 80 questions on the test, sam got 56 correct in order to get a 70%.
To find this, you must find 70 percent of 80 questions. You first must turn 70% into a decimal, making it 0.70. You multiply this decimal by the 80 questions on the test. You then get 56. Meaning they got 56 right. I hope this helps!
Write the expression as a number in scientific notation.
quantity 7 times 10 cubed end quantity times quantity 5.4 times 10 to the fourth power end quantity all divided by quantity 9 times 10 squared
4.2 x 1010
3.4 x 1010
4.2 x 105
3.4 x 105
Answers
The expression as a number in scientific notation is 4.2 * 10^5
How to write the expression as a number in scientific notation?The expression is given as:
quantity 7 times 10 cubed end quantity times quantity 5.4 times 10 to the fourth power end quantity all divided by quantity 9 times 10 squared
Rewrite properly as:
[7 * 10^3 * 5.4 * 10^4]/[9 * 10^2]
Evaluate the product of 7 and 5.4
So, we have:
[37.8* 10^3 * 10^4]/[9 * 10^2]
Evaluate the product of 10^3 and 10^4
So, we have:
[37.8* 10^7]/[9 * 10^2]
Evaluate the quotient of 37.8 and 9
So, we have:
[4.2 * 10^7]/[10^2]
Evaluate the quotient of 10^7 and 10^2
So, we have:
4.2 * 10^5
Hence, the expression as a number in scientific notation is 4.2 * 10^5
Read more about scientific notation at
https://brainly.com/question/5756316
#SPJ1
what dose x stand for 11 + x/9 = 4
Answers
Answer:-63
Step-by-step explanation:
well first you would do 4-11 which is -7 and then -7x9=-63
Answer:
-63
Step-by-step explanation:
1. Subtract 11 from both sides:
\(\frac{x}{9} =-7\)
2. Multiply both sides by 9 to isolate x:
\((9)\frac{x}{9} =-7(9)\)
x = -63
hope this helps!
Two power plants are currently emitting 8,000 tonnes of pollution annually each (totalling 16,000 tonnes of pollution). Pollution reduction costs for Plant 1 are given by MCC1 = 0.02Q and for Plant 2 by MCC2 = 0.03Q, where Q represents the number of tonnes of pollution reduction.
a) Suppose a regulation is implemented that requires each plant to reduce its pollution by 5,000 tonnes. What will be each firm's pollution control costs? Draw two graphs (one for each firm) to support your answer. (25 marks)
b) Suppose instead that a pollution tax of $120 per tonne of pollution emitted is implemented. How much will each firm now pay in pollution reductions costs (not considering taxes)? How do total pollution reduction costs with the tax compare to the costs calculated in part a? Explain why the costs differ. How much does each firm pay in taxes? Draw two graphs (one for each firm) to support your answer. (25 marks)
c) Finally, suppose that a tradeable permit scheme is instituted in which permits for emissions of 6,000 tonnes are freely issued, 3,000 permits to each plant. What are the pollution reduction costs to each firm without trading? Use a graph to support your answer, showing 10,000 tonnes of total pollution reduction. (25 marks)
d) Using the same diagram from part c, explain which firm will sell permits (and how many), and which firm will buy permits. Assuming all permits sell for the same price, how much will each permit cost? Calculate each firm's costs after trading, considering their pollution reduction costs and the costs (or revenues) from the permit sale
Answers
a) If each plant is required to reduce its pollution by 5,000 tonnes, we can calculate the pollution control costs for each firm using the given marginal cost curves. For Plant 1, MCC1 = 0.02Q, where Q represents the tonnes of pollution reduction. Similarly, for Plant 2, MCC2 = 0.03Q.
For both firms, since the pollution reduction is fixed at 5,000 tonnes, we substitute Q = 5,000 into the respective marginal cost curves:
MCC1 = 0.02 * 5,000 = $100
MCC2 = 0.03 * 5,000 = $150
Therefore, Plant 1's pollution control costs will be $100 and Plant 2's pollution control costs will be $150.
The graph for Plant 1 will have a linearly increasing slope starting from the origin, and the graph for Plant 2 will have a steeper linearly increasing slope starting from the origin.
b) With a pollution tax of $120 per tonne of pollution emitted, each firm's pollution reduction costs will be affected. The firms will now have to pay the pollution tax in addition to their pollution control costs.
Without considering taxes, Plant 1's pollution control costs were $100, and Plant 2's costs were $150 for a total of $250. However, with the pollution tax, the costs will change. Let's assume the firms still need to reduce their pollution by 5,000 tonnes.
For Plant 1: Pollution control costs = MCC1 * Q = 0.02 * 5,000 = $100 (same as before)
Total costs for Plant 1 = Pollution control costs + (Tax per tonne * Tonnes of pollution emitted)
Total costs for Plant 1 = $100 + ($120 * 5,000) = $610,000
Similarly, for Plant 2: Pollution control costs = MCC2 * Q = 0.03 * 5,000 = $150 (same as before)
Total costs for Plant 2 = Pollution control costs + (Tax per tonne * Tonnes of pollution emitted)
Total costs for Plant 2 = $150 + ($120 * 5,000) = $750,000
The total pollution reduction costs with the tax are now $610,000 for Plant 1 and $750,000 for Plant 2, resulting in higher costs compared to part a. This difference arises because the tax imposes an additional financial burden on the firms based on their emissions.
To support this answer, we can draw two graphs, one for each firm, with the tonnes of pollution emitted on the x-axis and the total costs on the y-axis. The graphs will show an increase in costs due to the tax.
c) In a tradable permit scheme where 6,000 permits are issued, with 3,000 permits to each plant, the pollution reduction costs to each firm without trading can be determined.
Since Plant 1 and Plant 2 each receive 3,000 permits, they can each emit up to 3,000 tonnes of pollution without incurring any additional costs. However, if they need to reduce their pollution beyond the allocated permits, they will have to incur pollution control costs as calculated in part a.
Learn more about marginal cost curves here: brainly.com/question/14434839
#SPJ11
Which is one quality of the entire open-ocean zone? few nutrients low pressure ample sunlight varying salinity
Answers
Few nutrients
I just took the test and this is the correct answer
The one quality of the entire open-ocean zone is few nutrients
What is the open-ocean zone?The open-ocean zone is the part of the sear where over half of the ocean is filled with water.
Because of the presence of water, there are only few nutrients that can be found on the entire open-ocean zone
Hence, the one quality of the entire open-ocean zone is few nutrients
Read more about open-ocean zone at:
https://brainly.com/question/15382223
given that the absolute value of the difference of the two roots of $ax^2 + 5x - 3 = 0$ is $\frac{\sqrt{61}}{3}$, and $a$ is positive, what is the value of $a$?
Answers
The value of "a" is approximately 1.83 given that the absolute value of the difference of the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive.
We are given that the absolute value of the difference between the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive. We need to find the value of "a".
Let the two roots of the equation be r1 and r2, where r1 is not equal to r2. Then, we have:
|r1 - r2| = √(61) / 3
The sum of the roots of the quadratic equation is given by r1 + r2 = -5 / a, and the product of the roots is given by r1 × r2 = -3 / a.
We can express the difference between the roots in terms of the sum and product of the roots as follows:
r1 - r2 = √((r1 + r2)² - 4r1r2)
Substituting the expressions we obtained earlier, we have:
r1 - r2 = √(((-5 / a)²) + (4 × (3 / a)))
Simplifying, we get:
r1 - r2 = √((25 / a²) + (12 / a))
Taking the absolute value of both sides, we get:
|r1 - r2| = √((25 / a²) + (12 / a))
Comparing this with the given expression |r1 - r2| = √(61) / 3, we get:
√((25 / a²) + (12 / a)) = √(61) / 3
Squaring both sides and simplifying, we get:
25 / a² + 12 / a - 61 / 9 = 0
Multiplying both sides by 9a², we get:
225 + 108a - 61a² = 0
Solving this quadratic equation for "a", we get:
a = (108 + √(108² + 4 × 61 × 225)) / (2 × 61)
Since "a" must be positive, we take the positive root:
a = (108 + √(108² + 4 × 61 × 225)) / (2 × 61) ≈ 1.83
Therefore, the value of "a" is approximately 1.83.
Learn more about absolute value at
https://brainly.com/question/1301718
#SPJ4
The question is -
Given that the absolute value of the difference of the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive, what is the value of "a"?
Which value is NOT equivalent to the other values?
A: 1.5
B: 15%
C: 3/20
D: 0.15
Answers
Answer:
A
Step-by-step explanation:
1.5 does not equal 0.15 or the other values.
NEED ANSWER ASAP‼️
Which of the following functions has a restricted domain?
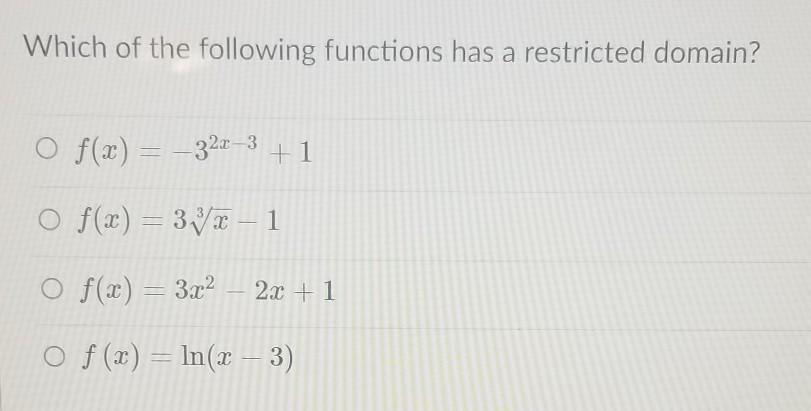
Answers
Answer:
ln(x - 3).
Step-by-step explanation:
f(x) = ln(x - 3)
For ln x, x must be > 0
so for ln(x - 3) , x must be > 3.
I NEED HELP QUICK, ANSWER FOR BRAINLIEST
What is the measure of angle B in this triangle?
Enter your answer in the box.
m∠B

Answers
Answer: 70 degrees
Step-by-step explanation: We know that the interior angles of a triangle add up to 180 degrees. The first step is to set up the equation and have all the angles add up to 180.
Step 1:
\(40+(x+20)+(2x-30)=180\)
Next combine like terms,
\(3x+30=180\)
Subtract 30 from both sides to isolate the x term
\(3x=150\)
Divide both sides to find the value of x
\(x=50\)
Now remember the question is asking us to solve for angle B, so just plug in the x value back into the angle value for B
\(B=2(50)-30\\=100-30\\=70\)