What is the measure of Angle A B C ? 36° 43° 72° 144°
Answers
Step-by-step explanation:
the correct answer is C because the measurementor an angle cannot be under 72 :)
Answer:
36
Step-by-step explanation:

Related Questions
Question
A farmer notices that there is a linear relationship between the number of bean stalks, n, she plants and the yield, Y. When
she plants 3 stalks, each plant yields 115 ounces of beans. When she plants 8 stalks, each plant yields 190 ounces of beans.
Write the linear equation, Y(n), that correctly represents this situation.
Provide your answer below:
Y(n)=
Content attribution
evious
FEEDBACK
MORE INSTRUCTION
SUBMIT
Answers
The equation that represent the given situation is y = 15x + 70
When she plants 3 stalks, each plant yields 115 ounces of beans
The first point = (3, 115)
When she plants 8 stalks, each plant yields 190 ounces of beans
The second point = (8, 190)
The slope of the line m = \(\frac{y_2-y_1}{x_2-x_1}\)
Substitute the values in the equation
The slope of the line m = (190-115) / (8-3)
= 75/5
= 15
The point slope form is
\(y-y_1=m(x-x_1)\)
Choose one point and substitute the values in the equation
y - 115 = 15(x - 3)
y - 115 = 15x - 45
y = 15x - 45 + 115
y = 15x + 70
Hence, the equation that represent the given situation is y = 15x + 70
Learn more about slope of the line here
brainly.com/question/16180119
#SPJ1
Explain how you use a net to find the surface area of a
prism?
Answers
Answer:
Lay the net out with the dimensions then multiply for each shape and add all of the areas to get the total surface area of your prism.
Step-by-step explanation:
this is how you work it out with the net
Answer:
You must lay out the net, find the area of each shape and multiply, and then add each dimension.
I really had some trouble with this problem:( & I need some help

Answers

find the midpoint of the line segment between the points (11, -5) and (-3, -7)
Answers
Answer:
(4, -6)
Step-by-step explanation:
(x1+x2)/2 + (y1+y2)/2 = midpoint
(11+-3)/2 = 8/2 = 4. x = 4
(-5 + -7)/2 = -12/2. y = -6
4, -6 is the midpoint
give brainliest please! hope this helps :)
Anna bought $4000of company stock, she sold 75% if it when the value doubled and the remainder at four times the purchase price, what is here total profit
Answers
Anna's total profit was $6000 + $16000 - $4000 = $14000.
How did Anna earn profit
Anna bought $4000 of company stock. The value of the stock doubled when she sold 75% of it, which means she sold 0.75 * $4000 = $3000 worth of stock when its value doubled.
Since the value of the stock doubled, Anna sold the $3000 worth of stock for 2 * $3000 = $6000.
Anna then sold the remainder of the stock (25% of the original amount) for four times the purchase price. Since she originally bought the stock for $4000, the remainder was worth 0.25 * $4000 = $1000.
Selling this remainder for four times the purchase price means that Anna sold it for 4 * $4000 = $16000.
Help help math math math math

Answers
Answer:
(-2,1)
Step-by-step explanation:
The solution of a system of equations is wherever the two lines intersect. So, this is quite easy. We can see they intersect at (-2,1). We can tell it is (-2,1) becuase it is two units left and one units up from the origin.
That is the solution.
(-2,1)
Answer:
The answer is (-2,1). Hope this helps :)
Step-by-step explanation:
In a very large population, a quantitative trait has the following distribution pattern. If there is no gene flow, the curve shifts to the left or to the right, and the population size consequently increases over successive generations, which of the following is most likely occurring?
Answers
The distribution of a quantitative trait in a population can have important implications for the size and composition of the population over time.
Quantitative traits are characteristics that can be measured and quantified, such as height or weight. These traits often have a normal distribution pattern in large populations, meaning that most individuals fall within a certain range and there are fewer individuals at the extremes.
The normal distribution of a quantitative trait is often represented by a bell curve. This curve shows the frequency of individuals at different values of the trait, with the majority of individuals falling near the middle of the curve and fewer individuals at the extremes. The mean, or average, of the trait is located at the peak of the curve, and the standard deviation determines the width of the curve.
If the distribution shifts to the left, this means that there are fewer individuals with high values of the trait and more individuals with low values. This could occur if there is selective pressure against individuals with high values, or if there is a genetic mutation that affects the trait in a negative way.
As a result, the population size may increase, as individuals with low values of the trait are more likely to survive and reproduce.
Conversely, if the distribution shifts to the right, this means that there are fewer individuals with low values of the trait and more individuals with high values.
This could occur if there is selective pressure in favor of individuals with high values, or if there is a genetic mutation that affects the trait in a positive way.
As a result, the population size may also increase, as individuals with high values of the trait are more likely to survive and reproduce.
To know more about distribution here.
https://brainly.com/question/29062095
#SPJ4
Hello random community i have a question to ask what is 7/8 - 3/4
Answers
Answer: 1/8
Step-by-step explanation:
First make the bottom half the same:
3/4*2/2=6/8
We don’t need to change the first portion since they have a common factor
7/8-6/8=1/8
In July of 1997, Australians were asked if they thought unemployment would increase, and 47% thought that it would increase. In November of 1997, they were asked again. At that time 284 out of 631 said that they thought unemployment would increase ("Morgan gallup poll," 2013). At the 5% level, is there enough evidence to show that the proportion of Australians in November 1997 who believe unemployment would increase is less than the proportion who felt it would increase in July 1997?
Answers
Answer:
\(z=\frac{0.45 -0.47}{\sqrt{\frac{0.47(1-0.47)}{631}}}=-1.007\)
Now we can find the p value with the alternative hypothesis and using this probability:
\(p_v =P(z<-1.007)=0.157\)
Since the p value is higher than the significance level given of 0.05 we have enough evidence to FAIL to reject the null hypothesis and we can conclude that the true proportion of interest is not significantly lower than 0.47
Step-by-step explanation:
Information given
n=631 represent the random sample selected
X=284 represent the people who said that they thought unemployment would increase
\(\hat p=\frac{284}{631}=0.45\) estimated proportion of people who said that they thought unemployment would increase
\(p_o=0.47\) is the value that we want to test
\(\alpha=0.05\) represent the significance level
z would represent the statistic
\(p_v{/tex} represent the p value
System of hypothesis
We want to verify if the proportion of Australians in November 1997 who believe unemployment would increase is less than the proportion who felt it would increase in July 1997 (0.47), then the system of hypothesis are:
Null hypothesis:\(p\geq 0.47\)
Alternative hypothesis:\(p < 0.47\)
The statistic would be given by:
\(z=\frac{\hat p -p_o}{\sqrt{\frac{p_o (1-p_o)}{n}}}\) (1)
Replacing the info given we got:
\(z=\frac{0.45 -0.47}{\sqrt{\frac{0.47(1-0.47)}{631}}}=-1.007\)
Now we can find the p value with the alternative hypothesis and using this probability:
\(p_v =P(z<-1.007)=0.157\)
Since the p value is higher than the significance level given of 0.05 we have enough evidence to FAIL to reject the null hypothesis and we can conclude that the true proportion of interest is not significantly lower than 0.47
can you please help me

Answers
Answer:
Angle ABC = 6x
Step-by-step explanation:
this is an isosceles triangle so the values of angle ACB and angle ABC are the same.
Determine if the two triangles are congruent. If they are, state how you know.
A.
AAS
B.
ASA
C.
SSS
D.
SAS
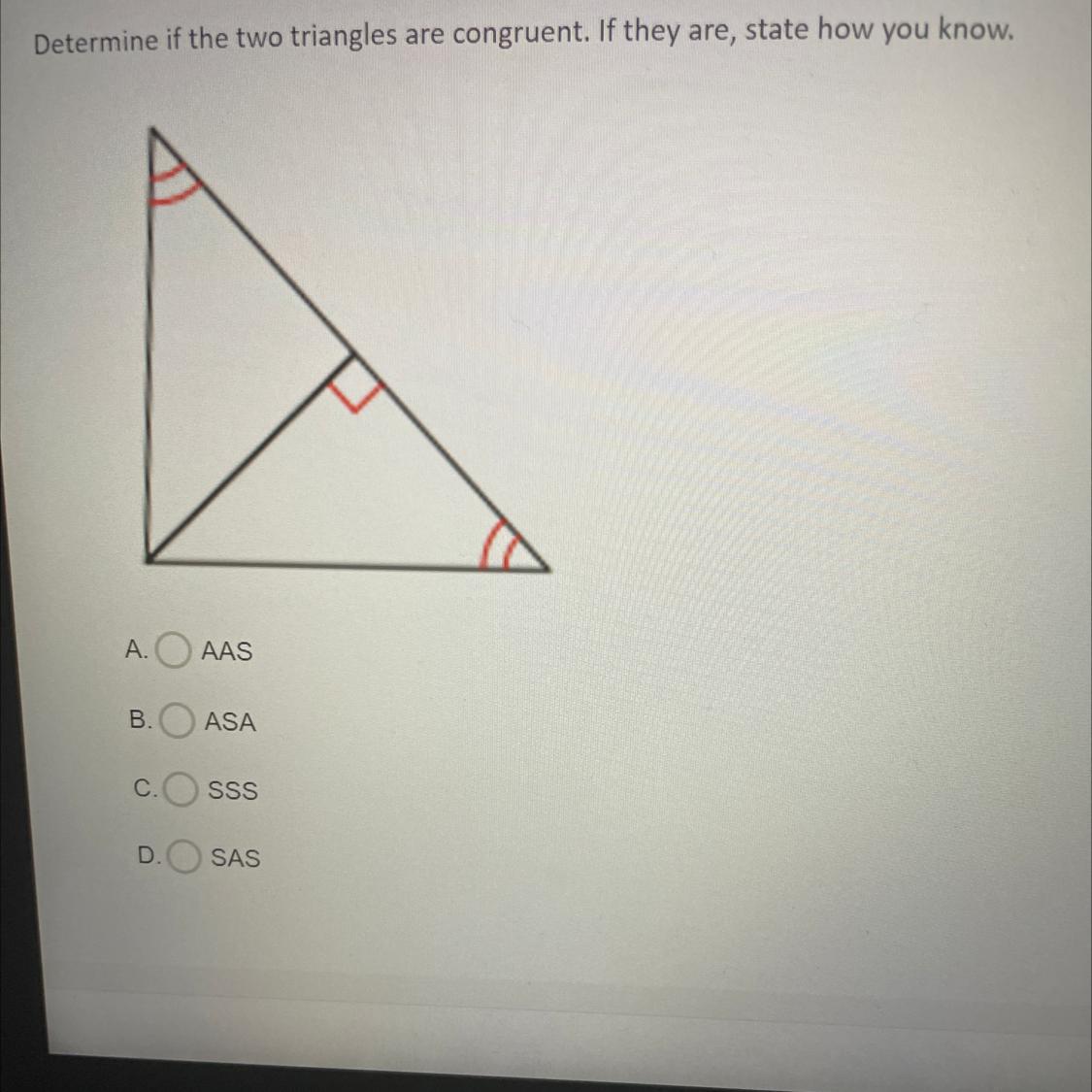
Answers
Answer:
not congruent
Step-by-step explanation
only one side has a 90 degree angle
What is the present value of R13 000 p.a. invested at the beginning of each year for 8years at 10%p.a. compound interest? (NB Use the compound interest tables provided or work to three decimal places only.)
Answers
Given statement solution is :- The present value of R13,000 per year invested for 8 years at 10% compound interest is approximately R69,776.60.
To calculate the present value of an investment with compound interest, we can use the formula for the present value of an annuity:
PV = A *\((1 - (1 + r)^(-n)) / r\)
Where:
PV = Present value
A = Annual payment or cash flow
r = Interest rate per period
n = Number of periods
In this case, the annual payment (A) is R13,000, the interest rate (r) is 10% per year, and the investment is made for 8 years (n).
Using the formula and substituting the given values, we can calculate the present value:
PV = \(13000 * (1 - (1 + 0.10)^(-8)) / 0.10\)
Calculating this expression:
PV = \(13000 * (1 - 1.10^(-8)) / 0.10\)
= 13000 * (1 - 0.46318) / 0.10
= 13000 * 0.53682 / 0.10
= 6977.66 / 0.10
= 69776.6
Therefore, the present value of R13,000 per year invested for 8 years at 10% compound interest is approximately R69,776.60.
For such more questions on present value
https://brainly.com/question/30390056
#SPJ8
Graph the line. pllzzzzzzzz

Answers
Answer:
Step-by-step explanation:
X: -2, -1, 0, 1, 2,...
Y: -2, -1, 0, 1, 2,...
(y=x)

A 2-gallon container of disinfectant costs $20.48. What is the price per cup?
Answers
Answer:
$0.64 per cup
Step-by-step explanation:
There are 16 cups in 1 gallon, so the number of cups in 2 gallons is:
1 gallon: 16 cups
2 gallon = 2 x 1 gallon = 2 x 16 cups = 32 cups
So we need to find the price of each cup:
1 cup = ($20.48 / 32 cups) = $0.64 per cup.
You buy a new computer for 2100. The computer decreases by 50% annually. How much is it worth after 2 years
Answers
Answer:V(t) = C·(0.5)t
Step-by-step explanation:
V(t) = computer's value at year t = 600
C = initial cost = 2100
t = years
Use the method of your choice to determine the probability below.
Being dealt three threes off the top of a standard deck of well-shuffled cards
Answers
Answer:
1/5525
Step-by-step explanation:
We now that a standard deck has 52 different cards. Also we know that a standard deck has four different suits, i.e., Spades, Hearts, Diamonds and Clubs. We can find the following cards for each suit: Ace, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen and King.
Now, the probability of getting any of these cards off the top of a standard deck of well-shuffled cards is 1/52. As we have 4 different sixes, we have that the probability of getting a six is 4/52. When we get a six, in the deck only remains 3 sixes and 51 cards, so, the probability of getting another six later is 3/51. When we get the second six, in the deck only remains 2 sixes and 50 cards, so, the probability of getting the third six is 2/50. As we have independet events, we should have that the probability of getting 3 sixes off the top of a standard deck of well-shuffled cards is
(4/52)(3/51)(2/50)=
24/132600=
12/66300=
6/33150=
3/16575=
1/5525
The required probability is 1/5525.
What is probability?Probability denotes the possibility of the outcome of any random event. The meaning of this term is to check the extent to which any event is likely to happen.
We now that a standard deck has 52 different cards.
Also we know that a standard deck has four different suits, i.e., Spades, Hearts, Diamonds and Clubs.
We can find the following cards for each suit: Ace, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen and King.
Now, the probability of getting any of these cards off the top of a standard deck of well-shuffled cards is 1/52.
As we have 4 different sixes, we have that the probability of getting a six is 4/52.
When we get a six, in the deck only remains 3 sixes and 51 cards, so, the probability of getting another six later is 3/51.
When we get the second six, in the deck only remains 2 sixes and 50 cards, so, the probability of getting the third six is 2/50.
As we have independent events, we should have that the probability of getting 3 sixes off the top of a standard deck of well-shuffled cards is
= (4/52)(3/51)(2/50)
= 24/132600
= 12/66300
= 6/33150
= 3/16575
= 1/5525
Hence the required probability is 1/5525.
Learn more about probability click;
https://brainly.com/question/30034780
#SPJ2
Both numbers have three significant figures. How many significant figures should be recorded for the answer to the division problem below?
\(43.6 \div 21.2\)
= [?] significant figures
Answers
Answer:
8 significant figures should be provided.
Step-by-step explanation:
I believe I am correct, but check your answer anyways.
Rafael wants to find the slope of the line

Answers
The correct formula for the slope will be:
m = (100 - 50)/(4 - 2) = 50/2 = 25 . Rafael took the reciprocal of the values.
Explain about the slope of the line?A line's slope is determined by how its y coordinate changes in relation to how its x coordinate changes. Δy and Δx are the net changes in the y and x coordinates, respectively.
So,
m = Δy / Δx
Using the slope-intercept form, as illustrated below, we can quickly get the slope for just a given line:
Y = mx + c can be used to represent a line.
where the slope's numerical value is m, the x-coefficient.A line's slope and steepness are both referred to as its slope.For the stated question:
The slope calculated by Rachel is:
m = (4 - 2) / (100 - 50) = 2/50 = 1/25
Which is incorrect .
Thus, the correct formula for the slope will be:
m = (100 - 50)/(4 - 2) = 50/2 = 25
know more about the slope of the line
https://brainly.com/question/16949303
#SPJ1
30 -35 points Workings please.
1. Find the equation of the tangent to the curve with equation
3x^2 + 2x - 5 at the point where x = - 2
2. At what point(s) on the curve with equation
y = 5x^3 is the tangent parallel to the line with equation 15x - 4y + 8 = 0 ?
Thank you for any help.
30 points (there are other questions differentiation similar on my profile.)
Answers
9514 1404 393
Answer:
10x +y +17 = 0(-1/2, -5/8), (1/2, 5/8)Step-by-step explanation:
1. The slope at any point on the curve can be found by differentiating the function.
f(x) = 3x^2 +2x -5
f'(x) = 6x +2 . . . . . derivative of f(x)
f'(-2) = 6(-2) +2 = -10
The value of the function at x=-2 is ...
f(-2) = 3(-2)^2 +2(-2) -5 = 3
So, we want the equation of the line with slope -10 through point (-2, 3). In point-slope form, that equation is ...
y -3 = -10(x +2) . . . . . . . point-slope equation of the tangent
10x +y +17 = 0 . . . . . . . tangent line in general form
__
2. The slope of the given line can be found by solving for y.
4y = 15x +8 . . . . . . add 4y
y = 15/4x +2 . . . . . divide by 4 . . . . . slope is 15/4
The curve has slope ...
y' = 15x^2
These slopes are equal when ...
15/4 = 15x^2
1/4 = x^2
±1/2 = x
The corresponding y-values are ...
y = 5(±1/2)^3 = ±5/8
The points where the tangent to the curve is parallel to the given line are ...
(-1/2, -5/8), (1/2, 5/8)


16m^2+60m-54
Factor
Answers
(a) Find the average and SD of the list 41, 48, 50, 50, 54, 57.
(b) Which numbers on the list are within 0.5 SDs of average? within 1.5 SDs of average? 2.
(a) Both of the following lists have the same average of 50. Which one has the smaller SD, and why? No computations are necessary. (i) 50, 40, 60, 30, 70, 25, 75 (ii) 50, 40, 60, 30, 70, 25, 75, 50, 50, 50
(b) Repeat, for the following two lists. (i) 50, 40, 60, 30, 70, 25, 75 (ii) 50, 40, 60, 30, 70, 25, 75, 99, 1
Answers
Answer:
1a) Mean = 40
Standard Deviation = 5
b)i Which numbers on the list are within 0.5 SDs of average?
48, 50, 50
ii) within 1.5 SDs of average?
48, 50, 50, 54, 57
2a)Both of the following lists have the same average of 50. Which one has the smaller SD, and why? No computations are necessary.
The list with the smaller S.D = (ii) 50, 40, 60, 30, 70, 25, 75, 50, 50, 50
This because the results obtained from the second list (ii) is close to the mean , therefore, the Standard deviation is small.
b) Repeat, for the following two lists.
The list with the smaller S.D = (i) 50, 40, 60, 30, 70, 25, 75
This because the results obtained from the second list (i) is close to the mean , therefore, the Standard deviation is small.
Step-by-step explanation:
1a) Find the average and SD of the list 41, 48, 50, 50, 54, 57.
Average (Mean) = Sum of terms/Number of terms
= 41+ 48 + 50 + 50+ 54 + 57/6
= 300/6
= 50
Standard Deviation for the population= √(x - Mean)²/n
=√ (41 - 50)²+ (48- 50)² + (50- 50)² +(50- 50)² + (54 - 50)² +(57- 50)²/6
= √81 + 4 + 0 + 0 + 16 + 49/6
= √150/6
= √25
= 5
(b) Which numbers on the list are within 0.5 SDs of average?
Mean ± Standard deviation × 0.5
50 ± 5 × 0.5
50 - 2.5
= 47.5
50 + 2.5
= 52.5
The numbers on the list are within 0.5 SDs of average are number within 47.5 and 52.5 : 48, 50, 50
ii) Within 1.5 SDs of average?
Mean ± Standard deviation × 1.5
50 ± 5 × 1.5
50 - 7.5
= 42.5
50 + 7.5
= 57.5
The numbers on the list are within 1.5 SDs of average are numbers within 42.5 and 57.5: 48, 50, 50, 54, 57
2 (a) Both of the following lists have the same average of 50. Which one has the smaller SD, and why? No computations are necessary.
(i) 50, 40, 60, 30, 70, 25, 75
Mean is already give as 50
Standard Deviation = √(x - mean)²/n
= √(50 - 50) + (40- 50)² (60 -50)² +(30- 50)² + (70 - 50)² + (25 - 50)² (75 - 50)² /n
= √0 + 100 + 100 + 400+ 400 + 625 + 625/7
= √2250/7
= √321.4285714
= 17.92842914
(ii) 50, 40, 60, 30, 70, 25, 75, 50, 50, 50
Standard deviation = √(x - mean)²/n
√(50 -50)²+(40-50)² + (60 -50)²+ (30-50)² + (70 - 50)²+ (25-50)² +(75-50)² + (50 -50)² + (50 - 50)²+(50 - 50)²/10
= √0 + 100 + 100 + 400 + 400 + 625 + 625 + 0 + 0 + 0/10
√2250/10
√225
= √15
The list with the smaller S.D = Second list (ii) 50, 40, 60, 30, 70, 25, 75, 50, 50, 50
This because the results obtained from the second list (ii) is close to the mean , therefore, the Standard deviation is small.
(b) Repeat, for the following two lists.
(i) 50, 40, 60, 30, 70, 25, 75
Mean is already give as 50
Standard Deviation = √(x - mean)²/n
= √(50 - 50) + (40- 50)² (60 -50)² +(30- 50)² + (70 - 50)² + (25 - 50)² (75 - 50)² /n
= √0 + 100 + 100 + 400+ 400 + 625 + 625/7
= √2250/7
= √321.4285714
= 17.92842914
(ii) 50, 40, 60, 30, 70, 25, 75, 99, 1
Standard Deviation = √(x - mean)²/n
= √(50-50)² +( 40 -50)² +( 60 - 50)² + (30 - 50)²+( 70 - 50)² + (25 - 50)² + (75 - 50)² +(99 - 50)² +(1 -50)²/9
= √0 + 100 + 100 + 400 + 400+ 625 + 625 + 2401 +2401/9
= √7052/9
= √783.5555556
= 27.99206237
The list with the smaller S.D = (i) 50, 40, 60, 30, 70, 25, 75
This because the results obtained from the first list(i) is close to the mean , therefore, the Standard deviation is small.
PLS HELP I NEED THE EQUATION IN SLOPE INTERCEPT Or POINT SLOPE FORMAT

Answers
Answer: \(y=\frac{3}{4}x+5.8\)
Step-by-step explanation:
We can think of this as a linear function with the slope being the 3/10 of a mile and the y intercept being the initial amount you can run.
So, using the information about 24 weeks, we get that:
\(13=\frac{3}{10}(24)+b\\\\b=5.8\)
So, the equation is \(y=\frac{3}{4}x+5.8\)
3. MODELING REAL LIFE An apple growing on a tree
has a circumference of 6 inches. (See Example 2.)
a. The apple has a density of 0.46 gram per cubic
centimeter. Find the mass of the apple.
b. The radius of the apple increases inch per week
for the next five weeks. How does the volume
change during the five-week period? Explain

Answers
a. The mass of the apple is approximately 33.879 grams.
b. The volume of the apple increases by approximately 1.454 cubic inches during the five-week period.
a. To find the mass of the apple, we need to calculate its volume first. The circumference of the apple can be used to determine its radius.
The formula for the circumference of a circle is C = 2πr,
where C is the circumference and r is the radius.
Rearranging the formula, we have r = C / (2π).
Plugging in the given circumference of 6 inches.
we get r = 6 / (2π) ≈ 0.955 inches.
Now, we need to convert the radius from inches to centimeters since the density is given in grams per cubic centimeter.
Since 1 inch is approximately 2.54 centimeters, the radius in centimeters is \(0.955 \times 2.54\) ≈ 2.427 cm.
Next, we can calculate the volume of the apple using the formula for the volume of a sphere: V = (4/3)πr³.
Plugging in the radius in centimeters, we get
V ≈ (4/3)π(2.427)³ ≈ 73.682 cm³.
Finally, we can find the mass of the apple by multiplying the volume by the density:
mass = volume \(\times\) density
= 73.682 cm³ \(\times\) 0.46 g/cm³
≈ 33.879 grams.
Therefore, the mass of the apple is approximately 33.879 grams.
b. The volume of a sphere increases with the cube of its radius.
Since the radius increases by 1/8 inch per week for five weeks, the change in radius would be\((1/8) \times 5 = 5/8 inch.\)
Now, let's calculate the change in volume during the five-week period. The formula for the volume of a sphere is V = (4/3)πr³.
Initially, the radius was 0.955 inches.
After five weeks, the radius would be 0.955 + 5/8 inches.
To compare the change in volume, we can calculate the new volume and find the difference:
Change in Volume = New Volume - Initial Volume
Initial Volume = (4/3)π(0.955)³
New Volume = (4/3)π(0.955 + 5/8)³
By subtracting the initial volume from the new volume, we can determine how the volume changes during the five-week period.
Please note that the exact calculation will depend on the precise values used for π and the measurements provided.
For similar question on volume.
https://brainly.com/question/12410983
#SPJ11
Arthur has been challenged to donate $50,000. He decides to donate exactly 50% of the money every day until less than $1 remains. Write a function that would represent this situation.
Answers
Answer:(-1/2^x)(50000)
Step-by-step explanation:
What is the area of the shaded part of the figure if =14
x
=
14
ft?
Use 3.14
3.14
to approximate π
π
.

Answers
The area of the shaded part is: 42.14 ft² .
Area of SquareArea = s²
Area of Quarter CircleArea = 1/4πr²
Thus:
Area of the shaded part of the figure = area of square - area of quarter circle
Area of shaded part = s² - 1/4πr²
s = 14 ft
r = 14 ft
Substitute
Area of shaded part = 14² - 1/4(3.14)(14²)
= 42.14 ft²
Therefore, the area of the shaded part is: 42.14 ft² .
Learn more about area of square on:
https://brainly.com/question/813881
Find the area of the shaded triangle, if the side of each square is 1 unit long.

Answers
Answer:
10 units²
Step-by-step explanation:
The shape is a triangle.
The area can be found by multiplying the base (in units) with height (in units) divided by 2.
base = 4 units
height = 5 units
\(\frac{4 \times 5}{2}\)
\(\frac{20}{2} =10\)
If 2 pounds of rib steak and 6 pounds of hamburger meat costs $12.30 and 3 pounds of rib steak and 2 pounds of hamburger meat costs $9.70, what is the cost per pound of each type of meat?
Answers
The cost per pound of rib steak is $2.40 and the cost per pound of hamburger meat is $1.25.
To find the cost per pound of each type of meat, we can set up a system of equations based on the given information.
Let's denote the cost per pound of rib steak as 'x' and the cost per pound of hamburger meat as 'y'.
From the first statement, we know that:
2x + 6y = 12.30 ---(Equation 1)
From the second statement, we know that:
3x + 2y = 9.70 ---(Equation 2)
Now we can solve this system of equations to find the values of 'x' and 'y'.
Multiplying Equation 1 by 3 and Equation 2 by 2 to eliminate the 'x' term, we get:
6x + 18y = 36.90 ---(Equation 3)
6x + 4y = 19.40 ---(Equation 4)
Subtracting Equation 4 from Equation 3, we get:
14y = 17.50
Dividing both sides by 14, we find:
y = 1.25
Substituting the value of 'y' back into Equation 1, we can solve for 'x':
2x + 6(1.25) = 12.30
2x + 7.50 = 12.30
2x = 4.80
x = 2.40
Therefore, the cost per pound of rib steak is $2.40 and the cost per pound of hamburger meat is $1.25.
for such more question on cost
https://brainly.com/question/8993267
#SPJ8
what the answer for this area?

Answers
Answer:
the answer is 105
Step-by-step explanation:
because 5×3=15 so 15×7 =105
Two car services charge different rates. A charges .60 per mile plus 3.00initial charge B charges .75 per mile mile traveled . the situation is modeled bu this system where x is the number of miles traveled and y is the charge for that distance ,in cents. How many miles must each car travel for the charges to be equal and ehat is the charge for that distance
Answers
The charges will be equal when each car travels 2000 miles. To find the charge for that distance, we substitute x = 2000 into either equation.
To determine the number of miles at which the charges for the two car services, A and B, are equal, we can set up an equation based on the given information.
Let's represent the charge for car service A as y_A and the charge for car service B as y_B. We can set up the following equations:
For car service A: y_A = 0.60x + 300 (in cents)
For car service B: y_B = 0.75x (in cents)
To find the number of miles at which the charges are equal, we set y_A equal to y_B and solve for x:
0.60x + 300 = 0.75x
Subtracting 0.60x from both sides:
300 = 0.15x
Dividing both sides by 0.15:
x = 300 / 0.15
x = 2000
Therefore, the charges will be equal when each car travels 2000 miles. To find the charge for that distance, we substitute x = 2000 into either equation. Let's use the equation for car service A:
y_A = 0.60(2000) + 300
y_A = 1200 + 300
y_A = 1500 cents or $15.00
So, when each car travels 2000 miles, the charges will be equal at $15.00.
For more questions on distance
https://brainly.com/question/28342342
#SPJ8
I AM BEGGING FOR HELPPPPPPLLLL

Answers
Answer:
It might be D not sure tho
Step-by-step explanation:
Answer:
D
Step-by-step explanation:
There are 8 ounces in a cup. Multiply 8 three times and 3 three times and add those together. Divide the answer by 8.