what is the radius of a circle inscribed in a 9-12-15 triangle?
Answers
The radius of the circle inscribed in a 9-12-15 triangle is 3 units
The radius of a circle inscribed in a 9-12-15 triangle can be found using the formula for the inradius (r) of a triangle:
r = A/s
where A is the area of the triangle, and s is the semi-perimeter of the triangle.
Step 1: Find the semi-perimeter (s)
s = (a + b + c) / 2
s = (9 + 12 + 15) / 2
s = 36 / 2
s = 18
Step 2: Find the area (A) of the triangle using Heron's formula:
A = √(s(s-a)(s-b)(s-c))
A = √(18(18-9)(18-12)(18-15))
A = √(18(9)(6)(3))
A = √(2916)
A = 54
Step 3: Find the inradius (r) using the formula r = A/s:
r = 54 / 18
r = 3
Therefore, the radius of the circle inscribed in a 9-12-15 triangle is 3.
TIP: A circle inscribed in a triangle is a circle that touches all three sides of the triangle exactly once, and it is positioned entirely within the triangle.
#SPJ11
Related Questions
what is the degree of the polynomial 3x4y3-3x2y-5x-7
Answers
Answer: it is B
Step-by-step explanation:
hope this helps!!
Find the value of h(-67) for the function below.
h(x) = -49x − 125
A.
-3,408
B.
3,158
C.
3,283
D.
-1.18
Answers
Answer:
B. 3,158
Step-by-step explanation:
h(x) = -49x − 125
Let x = -67
h(-67) = -49(-67) − 125
=3283-125
= 3158
Answer:
Answer B
Step-by-step explanation:
To find the value of h(-67) for the function h(x) = -49x - 125,
we substitute -67 for x in the function and evaluate it.
h ( - 67 ) = - 49 ( - 67 ) - 125
Now we can simplify the expression:
h ( -67 ) = 3283 - 125
h ( -67 ) = 3158
6 ( x + 1) - 5 (x + 2)
Answers
Answer:
x-4
Step-by-step explanation:
6x+6-5x-10=
x-4
( you have to multiply what is inside the parenthases to get to the first step that i did)
Answer:
x−4
Step-by-step explanation:
what extra step do you need to take when using the Multiplication Property of Inequality and the Division Property of Inequality when the coefficient of the variable term is negative? Give an example to illustrate your reasoning. Algebra 1... I need this before tomorrow pls help
Answers
Answer:
Step-by-step explanation:
I appreciate this a bunch :))
Answers
Answer:
b = 72
Step-by-step explanation:
7/12b - 19 = 23
7/12b = 42
b = 72
Let's Check
7/12(72) - 19 = 23
42 - 19 = 23
23 = 23
So, b = 72 is the correct answer.
Need help with these two problems
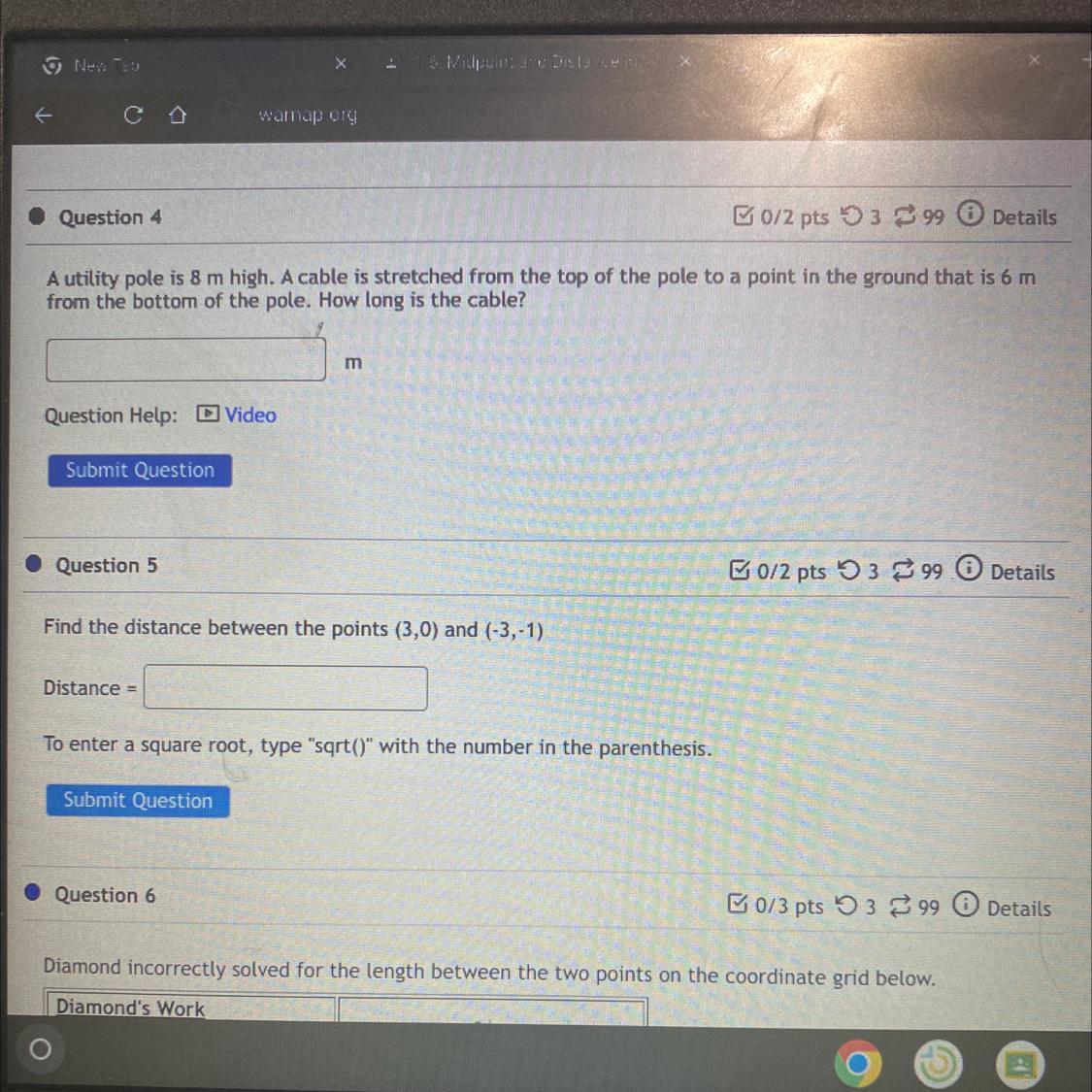
Answers
Answer:
Question 4 : 10 m
Question 5 : Square root 37
Step-by-step explanation:
QUESTION 4: So for the this one here we need to make a drawing (unfortunately). Lets break down the question because having a math problem with a ton of words is confusing sometimes. So we have a pole that is 8m high, so we can draw that out. So we take some cable and go 6 m from the bottom of the pole. So now we want to know how long the cable is and if we go from the top of the pole to the bottom 6m away it looks like this. (Below I'll put what I have written) Since now it's a 90 degrees angle there is a specific formula we can use in situations like this. Where we know 2 sides and need 1 more. a^2 + b^2 = c^2 should look familiar if it doesn't its all good! :D a^2 + b^2 = c^2 is called 'Pythagorean's theorem' (we don't really need to know that part) but basically we use it whenever we need to figure out a side when we already know the other two. We know that the straight line is 8, and the horizontal line is 6. So we can use that formula to get the last number. just know that whenever we have the right triangle, we can use the a^2 + b^2 = c^2 to get all the sides for it. The a and b in the formula are always the straight lines. The c is always the slanted line (the red line I drew). We don't know what it is, so we'll just put c^2 into our equation but we can solve for it! So 8^2 would equal to 64. 6^2 would equal to 36. 64 + 36 here gets us 100. Here's another trick you might need to memorize. Whenever there is a number squared like c^2, we can take the square root of both sides to get rid of it. So c^2 just becomes c. It's a little weird but very useful to remember. But if you remember the a^2 + b^2 = c^2 and use that square root technique you can get an A+ every time. :D Now all we need to know is the square root of 100. It's a big one so using a calculator is fine, here its just 10. Therefore our answer is 10.
QUESTION 5: We'll start off by reading 'distance between points' is a big thing to note here. There is a formula that we can directly use here. (I'll write under the picture in black). So distance between points always uses this formula: (In black). Okay, so the formula in black has more letters in it (which sucks) but we can break it down. When we have numbers like this (3, 0) it means (x, y). So I wrote down what the x1, y1, x2, y2, are here. X1 is just the first number, y1 is the second, x2 is the third, and y2 is the fourth. I just plugged in all the numbers from above in the order we put (x2, x1, y2, y1). Basically we can just solve this now! As of right now we'll need to solve (-3 -3)^2 when we solve that we should get 36. Next we're gonna solve (-1 - 0)^2 and we should get the answer of 1. Now we need to solve 36 +1 and we should know that it equals 37. Therefore we'd get answer: square root 37.
24. A pizzeria sells a medium pizza for $5.99 plus $0.75 for each topping.
They also sell a large pizza for $6.99 plus an additional $0.50 per topping.
After how many toppings will the medium and large pizzas cost the same
amount?
The pizzas will cost the same at 4 toppings.
The pizzas will cost the same at 5 toppings.
The pizzas will cost the same at 6 toppings.
The pizzas will never cost the same amount.
Answers
Answer:
a.) The pizzas will cost the same at 4 toppings
Step-by-step explanation:
Medium Pizza:
$5.99 + $0.75x
Large Pizza:
$6.99 + $0.50x
Find x
$5.99 + $0.75x = $6.99 + $0.50x
0.25x = 1
x = 4
Solve the following linear programming problem (LPP) using the Big-M method:
Maximize Z = 4x1 + 3x2
Subject to:
2x1 + x2 ≥ 10
-3x1 + 2x2 ≤ 6
x1 + x2 ≥ 6
x1, x2 ≥ 0
Answers
The optimal solution for the given linear programming problem using the Big-M method is x₁ = 4, x₂ = 2, with a maximum value of Z = 22.
To solve the given linear programming problem using the Big-M method, we first convert it into standard form by introducing slack, surplus, and artificial variables.
The objective function is to maximize Z = 4x₁ + 3x₂. The constraints are 2x₁ + x₂ ≥ 10, -3x₁ + 2x₂ ≤ 6, x₁ + x₂ ≥ 6, and x₁, x₂ ≥ 0.
We introduce slack variables s₁, s₂, and s₃ to convert the inequalities into equalities. The initial Big-M tableau is set up with the coefficients and variables, and the artificial variables are introduced to handle the inequalities. We set a large positive value (M) for the artificial variables' coefficients.
In the first iteration, we choose the most negative coefficient in the Z-row, which is -4 corresponding to x₁. We select the s₂-row as the pivot row since it has the minimum ratio of the RHS value (6) to the coefficient in the pivot column (-3). We perform row operations to make the pivot element 1 and other elements in the pivot column 0.
After multiple iterations, we find that the optimal solution is x₁ = 4, x₂ = 2, with a maximum value of Z = 22. This means that to maximize the objective function, x₁ should be set to 4 and x₂ should be set to 2, resulting in a maximum value of Z as 22." short
To know more about constraints visit -
brainly.com/question/33150163
#SPJ11
ii.) 2 ( x + 3 ) = 15
Answers
Answer:
2(x+3)=15
2x+6=15
2x=9
x= 4.5
Step-by-step explanation:
please pass this on... ( #helpsavelives )
Who ever is reading this:
I love u.
U matter.
The world needs u
hang in there ik it may be bad but u deserve the world <3
ur beautiful no matter ur shape, size, color, gender.. anything
don't give up i need u to live.
i wish i could take everyones problems so yall wouldn't have to have em but i cant so just know ily and if anyone needs to talk u can talk to me
Pls pass this on. Everyone deserves to know this. ♥️♥️
just copy and paste its not hard pls this could save someones life
In the diagram below, ΔABC≅ΔSTR. Complete the statement ∠A≅
A. ∠C
B. ∠S
C. ∠T
D. ∠R
Answers
Answer:
b
Step-by-step explanation:
Answer: B <S
Step-by-step explanation:
Dylan needed to get his computer fixed. He took it to the repair store. The technician at the store worked on the computer for 5.5 hours and charged him $71 for parts. The total was $648.50. What was the cost of labor, per hour?
Answers
Answer:
$105 per hour
Step-by-step explanation:
$648.50 - $71 = $577.50
$577.50 / 5.5 = $105 per hour
105 x 5.5 = 575.50
+ 71.00
648.50
The per hour charge of the technician is given as $15.
What is the application ratio and proportion?A ratio is the relation between two numbers as a / b. A proportion is the equality of two ratios as a / b = c / d.
Ratio and proportion can be applied to solve Mathematical problems dealing with unit values of the quantities.
The given problem can be solved by ratio method as follows,
The remaining cost charged by the technician is $648.50 - $71 = $577.50
Now, the per hour charge is remaining cost divided by total number of hours as given below,
577.50/5.5
= 57750/550
= 15
Hence, the cost of labor per hour is given as $15.
To know more about ratio and proportion click on,
brainly.com/question/14279414
#SPJ2
help. I can't do maths again
Answers
Answer:
x ≈ 14.4 cm
Step-by-step explanation:
the third angle of the triangle = 180° - 40° - 46° = 94°
Using the Sine rule in the triangle
\(\frac{x}{sin46}\) = \(\frac{20}{sin94}\) ( cross- multiply )
x × sin94° = 20 × sin46° ( divide both sides by sin94° )
x = \(\frac{20sin46}{sin94}\) ≈ 14.4 cm ( to the nearest tenth )
Answer:
14 cm (rounded to nearest whole number)
Step-by-step explanation:
Law of Sine:
\(\displaystyle \large{\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c} = 2R}\)
a,b,c are side lengths.R is radius so 2R is diameter.A,B,C are angles.Given angles are:
40°, 46°Definition of Euclidean Triangle:
Sum of three interior angles equals 180°Find another angle:
40°+46°+B = 180°86+B = 180B = 180-86B = 94°So another angle is 94°.
To find:
Value of xDetermine:
A = 46°a = x cmB = 94°b = 20 cmTherefore:
\(\displaystyle \large{\dfrac{\sin 46^{\circ}}{x} = \dfrac{\sin 94^{\circ}}{20}}\)
Multiply both sides by 20x:
\(\displaystyle \large{\dfrac{\sin 46^{\circ}}{x} \cdot 20x = \dfrac{\sin 94^{\circ}}{20} \cdot 20x}\\\displaystyle \large{20\sin 46^{\circ}= x\sin 94^{\circ}}\)
Divide both sides by \(\displaystyle \large{\sin 94^{\circ}}\):
\(\displaystyle \large{\dfrac{20\sin 46^{\circ}}{\sin 94^{\circ}} = \dfrac{x\sin 94^{\circ}}{\sin 94^{\circ}}}\\\displaystyle \large{\dfrac{20\sin 46^{\circ}}{\sin 94^{\circ}} = x}\)
Evaluate the expression, hence:
\(\displaystyle \large{x = 14.42...}\)
Round to nearest whole number:
\(\displaystyle \large{x = 14}\)
Therefore, the value of x is 14 cm.
true or false: as the level of confidence increases the number of item to be included in a sample will decrease when the error and the standard deviation are held constant.
Answers
The given statement "As the level of confidence increases the number of item to be included in a sample will decrease when the error and the standard deviation are held constant." is False because error increases.
As the level of confidence increases, the required sample size will increase when the error and standard deviation are held constant.
This is because as the level of confidence increases, the range of the confidence interval also increases, which requires a larger sample size to ensure that the estimate is precise enough to capture the true population parameter with the desired level of confidence.
For example, if we want to estimate the mean height of a population with a 95% confidence interval and a margin of error of 1 inch, we would need a larger sample size than if we were estimating the same mean height with a 90% confidence interval and the same margin of error.
The larger sample size ensures that the estimate is more precise and that we have a higher level of confidence that it captures the true population parameter.
To learn more about confidence click on,
https://brainly.com/question/31317533
#SPJ4
what is the probability that z is between 1.57 and 1.87
Answers
The probability that z is between 1.57 and 1.87 is approximately 0.0275. This would also give us a result of approximately 0.0275.
Assuming you are referring to the standard normal distribution, we can use a standard normal table or a calculator to find the probability that z is between 1.57 and 1.87.
Using a standard normal table, we can find the area under the curve between z = 1.57 and z = 1.87 by subtracting the area to the left of z = 1.57 from the area to the left of z = 1.87. From the table, we can find that the area to the left of z = 1.57 is 0.9418, and the area to the left of z = 1.87 is 0.9693. Therefore, the area between z = 1.57 and z = 1.87 is:
0.9693 - 0.9418 = 0.0275
So the probability that z is between 1.57 and 1.87 is approximately 0.0275.
Alternatively, we could use a calculator to find the probability directly using the standard normal cumulative distribution function (CDF). Using a calculator, we would input:
P(1.57 ≤ z ≤ 1.87) = normalcdf(1.57, 1.87, 0, 1)
where 0 is the mean and 1 is the standard deviation of the standard normal distribution. This would also give us a result of approximately 0.0275.
Learn more about probability here
https://brainly.com/question/13604758
#SPJ11
factor completely 64^2 - 1
Answers
Answer:
4095
Step-by-step explanation:
Find the equation of the tangent line to the graph of f(x) at the given point. f(x)= √(12x+24) at (1,6) The equation of the tangent line to the graph of f(x) at the given point is
Answers
The equation of the tangent line to the graph of f(x) at the point (1,6) is y = 3x + 3.
To find the equation of the tangent line, we need to determine the slope of the tangent line and the point of tangency.
First, we find the derivative of f(x) using the power rule. The derivative of √(12x+24) with respect to x is (1/2)(12x+24)^(-1/2) * 12, which simplifies to 6/(√(12x+24)).
Next, we evaluate the derivative at x=1 to find the slope of the tangent line at the point (1,6). Plugging in x=1 into the derivative, we get 6/(√(12+24)) = 6/6 = 1.
So, the slope of the tangent line is 1.
Using the point-slope form of a line, y - y1 = m(x - x1), where (x1, y1) is the point of tangency, we substitute (1,6) and the slope of 1 to obtain the equation of the tangent line as y = 1(x-1) + 6, which simplifies to y = x + 5.
To learn more about derivative click here
brainly.com/question/25324584
#SPJ11
Connor is a 400m runner His median time is
Answers
Answer: 57.8
Step-by-step explanation:48.7 seconds + 49.3 seconds.= 57.8
Scrieti rezultatul sub forma de fractie ireductabila : a)1/4+5/4; b) 23/17+11/17;c) 16/93+15/93;11/14+23/14;3/16+ 15/16 ; 1 1/8+1 3/8; 1 3/10+3 1/10;2 3/5+3 2/5 ;
Answers
Answer:
See explanations below
Step-by-step explanation:
a) 1/4+5/4
= (1+5)/4
= 6/4
= 3/2
b) 23/17+11/17
= (23+11)/17
= 34/17
= 2
c) 16/93+15/93
= (16+15)/93
= 31/93
= 1/3
d) 11/14+23/14
= (11+23)/14
= 34/14
= 17/7
e) 3/16+15/16
= (3+15)/16
= 18/16
= 9/8
f) 1 1/8 + 1 3/8
= 9/8 + 11/8
= (9+11)/8
= 20/8
= 5/2
g) 1 3/10+3 1/10;
= 13/10+31/10
= (13+31)/10
= 44/10
h) 2 3/5+3 2/5
= 13/5+17/5
= (13+17)/5
= 30/5
= 6
I WILL GIVE U BRANLIEST What is the coefficient of x^2 in the simplified product of
(3x^2 + x-2)(x - 5)?
Answers
Answer:
-14
Step-by-step explanation:
Okay first we must simplify the expression.
so this:(3x^2 + x-2)(x - 5)
becomes this:3x^3-14x^2-7x+10
then we look at the coefficient of x^2 and we see that it's -14
Answer:
-14
Step-by-step explanation:
the person above explained it well, have a nice day!
Find the measure of the interior and exterior angles of a regular 17-gon
please help me
Answers
The measurements of interior and exterior angles of a regular 17-gon are 158.82° and 21.17°, respectively.
What is a polygon?A polygon is a two-dimensional geometric figure that has a finite number of sides.
Given that, we need to find the measurement of interior and exterior angles of a regular 17-gon,
The sum of interior angles of a polygon is given by:
Sum = (n-2) × 180°
= (17-2) × 180°
= 15 × 180°
= 2700°
One angle measure = 2700 / 17
= 158.82°
Since, we know that, the sum of exterior angle of any polygon is 360°,
Therefore,
One angle measure = 360° / 17 = 21.17°
Hence, the measurements of interior and exterior angles of a regular 17-gon are 158.82° and 21.17°, respectively.
Learn more about polygons, click;
https://brainly.com/question/24464711
#SPJ1
You construct a tangent to circle O at point X on the circle, as shown below. What do you expect to be the measure of ∠OXY?
Answers
Answer: 90 Degrees :)
Step-by-step explanation:
Ur Welcome ;)
what fraction of 5 is 1/2
Answers
Answer:
1/10
Step-by-step explanation:
1/2 divided by 5 = 1/10
Answer:
2 1/2
Step-by-step explanation:
Suppose in order for a bill to pass in Congress, 50% of voters must be in favor of it. In a random sample of 150 voters, 62 said that they were in favor of a new bill. State the p-value assuming the alternative hypothesis is Ha ≠.50 (Round to the nearest hundredth.)
Answers
Using the z-distribution, it is found that the p-value is of 0.03.
At the null hypothesis, it is tested if the proportion is of 0.5, that is:
\(H_0: p = 0.5\)
At the alternative hypothesis, it is tested if the proportion is different of 0.5, that is:
\(H_a: p \neq 0.5\)
The test statistic is given by:
\(z = \frac{\overline{p} - p}{\sqrt{\frac{p(1-p)}{n}}}\)
In which:
\(\overline{p}\) is the sample proportion. p is the proportion tested at the null hypothesis. n is the sample size.For this problem, the parameters are: \(p = 0.5, n = 150, \overline{p} = \frac{62}{150} = 0.4133\)
Hence, the value of the test statistic is:
\(z = \frac{\overline{p} - p}{\sqrt{\frac{p(1-p)}{n}}}\)
\(z = \frac{0.4133 - 0.5}{\sqrt{\frac{0.5(0.5)}{150}}}\)
\(z = -2.12\)
The p-value is found using a z-distribution calculator, with z = -2.12 and a two-tailed test, as we are testing if the mean is different of a value, hence it is of 0.03.
To learn more about the use of the z-distribution for hypothesis tests, you can take a look at https://brainly.com/question/16313918
Compute the directional derivative of the functionf(x,y)=2xy−3y2,at the point P0=(5,5)in the direction of the vector u = 4i + 3j.
Answers
The directional derivative of the function f(x,y) = 2xy - 3y^2 at the point P0 = (5,5) in the direction of the vector u = 4i + 3j is 6√2.
Explanation:
The directional derivative measures the rate of change of a function in a specific direction. It is denoted by ∇_u f(x,y), where u is the unit vector in the direction of interest. To compute the directional derivative, we need to take the dot product of the gradient of f with the unit vector u.
First, we need to find the gradient of f(x,y).
∇f(x,y) = [2y, 2x - 6y]
Next, we need to normalize the vector u to get the unit vector in the direction of interest.
|u| = √(4^2 + 3^2) = 5
u^ = (4/5)i + (3/5)j
Taking the dot product of the gradient of f with the unit vector u, we get:
∇_u f(x,y) = ∇f(x,y) · u^ = [2y, 2x - 6y] · (4/5)i + (3/5)j
At the point P0 = (5,5), we have:
∇_u f(5,5) = [2(5), 2(5) - 6(5)] · (4/5)i + (3/5)j = 10(4/5) + (-6)(3/5) = 8 - 3.6 = 4.4
Therefore, the directional derivative of f(x,y) at the point P0 = (5,5) in the direction of the vector u = 4i + 3j is:
∇_u f(5,5) = 4.4
Finally, we need to scale the result by the magnitude of the vector u to get the directional derivative in the direction of u.
Directional derivative = ∇_u f(5,5) / |u| = 4.4 / 5 = 0.88 * √(2)
Directional derivative = 6√2.
To learn more about dot product click here, brainly.com/question/29097076
#SPJ11
A rectangle has a length of 14 units and a width of 6 units. Squares of x by x units are cut out of each corner, and then the sides are folded up to create an open box. Express the volume of the box as a polynomial function in terms of x.
Answers
Answer:
f(x) = 4x³ - 40x² + 84x=================================
The box is the right rectangular prism.
Its volume is the product of its three dimensions:
V = lwhWe need to find each dimension and multiply them to get the desired function.
GivenLength = 14 units,Width = 6 units,Cut = x units.SolutionThe height is same as size of the cut, so it is x units.
h = xThe length was 14 units but it is now cut from bot ends so it is now:
l = 14 - 2xThe width was 6 units but it is too cut from the both ends by x units:
w = 6 - 2xWe have all three dimensions, find the volume:
f(x) = x(6 - 2x)(14 - 2x) or, when distributedf(x) = x(6*14 - 6*2x - 2x*14 + 2x*2x) = x(4x² - 40x + 84) = 4x³ - 40x² + 84xV = (14 - 2x) (6 - 2x) x cubic units.
The polynomial function formed by given dats is V=(14 - 2x) (6 - 2x) x
What is polynomial function?A polynomial function is one that involves only non-negative integer powers or only positive integer exponents of a variable in an equation such as the quadratic equation, cubic equation, or exponential equation.
Here given,
A rectangle has 14 units of length and 6 units of width.
From each corner of the rectangle, four squares with dimensions of x by x units are cut out.
The box's length is equal to (14 - 2x) units.
The box's width is =(6 - 2x) units.
The box's height is = x unit.
The volume of the box is equal to the sum of its length, width, and height.
Cubic units =(14 - 2x) (6 - 2x) x
∴V=(14 - 2x) (6 - 2x) x
where V is the box's volume in cubic units
To learn more about polynomial function refer to :
https://brainly.com/question/7693326
#SPJ9
Find the derivative of the function with solutions.y = In( e^(3 - x^2 ) + 9 ))
Answers
Answer:
\(\frac{dy}{dx}=-\frac{2xe^{3-x^2}}{e^{3-x^2}+9}\)Explanation:
We were given the function:
\(y=\ln\left(e^{3-x^2}+9\right)\)We are to find the derivative of this function, we have it shown below:
\(\begin{gathered} y=\operatorname{\ln}(e^{3-x^{2}}+9) \\ If:y=ln(u) \\ Then:y^{\prime}=\frac{u^{\prime}}{u} \\ y^{\prime}=\frac{dy}{dy} \\ u=e^{3-x^2}+9 \\ u^{\prime}=-2xe^{3-x^2} \\ y^{\prime}=\frac{u^{\prime}}{u} \\ \Rightarrow y^{\prime}=\frac{-2xe^{3-x^2}}{e^{3-x^2}+9} \\ But:y^{\prime}=\frac{dy}{dx} \\ \frac{dy}{dx}=-\frac{2xe^{3-x^2}}{e^{3-x^2}+9} \\ \\ \therefore\frac{dy}{dx}=-\frac{2xe^{3-x^2}}{e^{3-x^2}+9} \end{gathered}\)the ratio of red marbles to yellow marbles placed in a bag is 2:7. More marbles are added to the bag: 3 red and 3 yellow marbles. Maria states that the ratio is still the same since equal amounts of red and yellow marbles were added to the bag
Answers
Answer: False.
Step-by-step explanation:
Initially, the ratio is 2:7
This means that if we have 2 red marbles, we must have 7 yellow ones.
The quotient here is 7/2 = 3.5
Now, if you add 3 marbles of each colour, then we have:
2 + 3 = 5 red marbles
7 + 3 = 10 yellow marbles.
Now the ratio is 5:10
This means that for every 5 red marbles, we have 10 yellow ones.
But now we can divide both numbers by the same positive integer, because they have a common factor equal to 5.
5/5 = 1
10/5 = 2
Then we have:
5:10 = 1:2
So the new ratio is 1:2
Then the ratio changed when we added the new marbles, which means that Maria was wrong.
im not sure ols help
Answers
Answer: √141
Step-by-step explanation:
a^2=c^2-b^2
The hypotenuse is larger in this question so we subtract them.
25^2-22^2=625-484=141
√141
Answer:
x = √141
or
x = 11.87
Step-by-step explanation:
is a right triangle, we solve it with the Pythagorean theorem ("In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides".)
x² = 25² - 22²
x² = 625 - 484
x² = 141
x = √141
or
x = 11.87
Choose the graph that matches the following system of equations: x–3y =-12, 2x - y = 1
Answers
Answer:
x=3, y=5
Step-by-step explanation:
A puppy named Boots started out at 4 pounds and gained 3 pounds every month. At how
many months did Boots weigh 25 pounds?
Answers
Answer: 7 months
Step-by-step explanation:
He started at 4 pounds so if he grew 3 pounds every month, it would take 7 months to grow 21 pounds. 21 pounds plus 4 pounds is 25 pounds.
Answer:
7 months
Step-by-step explanation:
3 times 7 is 21 than you add the original 4 and get 25 so therefore the answer is 7 months