Answers
Answer:
the Awnswer is 2
Step-by-step explanation:
A. The scale factor is 2, and the center of dilation is point B.
Related Questions
The square below represents one whole.What percent is represented by the shaded area?

Answers
You won't type in the percent sign as that's already taken care of
=============================================================
Explanation:
We have 6 squares shaded out of 100 total. This means we have 6/100 = 0.06 = 6% of the squares shaded. The term "percent" means "per 100" or "for every 100".
Take note that there are 10 rows and 10 columns, meaning there are 10*10 = 100 squares total, either shaded or not shaded.
Find the value of X using your method

Answers
Answer:
\(x = 30\)
Step-by-step explanation:
In the diagram above, MN is a straight line which equals 180.
RL is vertically opposite to KS
(Vertically opposite angles are equal ⟹RL = KS).
So, MN becomes:
\(90 + 2x + 30 = 180\)
Collect like terms
\(90 + 30 + 2x = 180→120 + 2x = 180→2x = 180 - 120→2x = 60\)
Divide 2x = 60 by 2
\(x = \frac{60}{2} \)
Therefore: \(x = 30\)
Optimization A cone is made from a circular sheet of radium R by cutting out a sector and gluing the cut edges. What is the maximum volume of the cone
Answers
The cone should have its maximum volume. V=1/*3r2h is the formula for calculating the volume V of a cone with height h and radius r.
How do you find the maximum volume of a cone?The cone has a volume of
V=πr2h/3
Therefore, we must calculate the values of r and h in terms of R. R is the diameter of the cone's top-circular circle, and h is the cone's height.
R is the cone's slant height, and it serves as the hypotenuse of a right triangle.
R2 = h2 + r2, or r2 = R2-h2.
So V = (1/3)π
[R2-h2]
h = (π/3)[R2h-h3]
You must take the derivative of the cone's volume, set it to zero, then solve for h to determine the cone's maximum volume.
dV/dh=(π/3)[R2-3h2]
R2-3h2=0 --> h2=R2/3 -> h = R/√3
Now we can determine r:
r2=R2-R2/3 = (2/3)R2
The volume formula with r and h substituted:
V = (π/3)
r2h = (π/3)(2R2/3)
(R/√3)
V(R)=2πR3/(9√3)
The complete question is:
A cone-shaped drinking cup is made from a circular piece of paper of radius R by cutting out a sector and joining the edges CA and CB. Find the maximum capacity of such a cup (Your answer may depend on R).
To learn more about volume of the cone refer to:
https://brainly.com/question/1082469
#SPJ4
4(2x+5)-2(x-3)=8(2x+4)
Answers
Answer:
-0.6 or -(3/5)
Step-by-step explanation:
Let's simplify the left-hand side of the equation first:
4(2x+5)-2(x-3)
= 8x + 20 - 2x + 6 [distributing the multiplication and simplifying the parentheses]
= 6x + 26
Now let's simplify the right-hand side of the equation:
8(2x+4)
= 16x + 32
So the equation becomes:
6x + 26 = 16x + 32
Let's isolate x on one side of the equation:
6x - 16x = 32 - 26
-10x = 6
x = -0.6
Therefore, the solution to the equation is x = -0.6.
The ratio of a pair of corresponding sides in two similar triangles is 5:3. The area of the smaller triangle is 108 in2. What is the area of the larger triangle?
Answers
Answer:
The hypotenuse of a right triangle is always the side opposite the right angle. It is the ... The other two sides are called the opposite and adjacent sides. ... functions—sine, cosine, and tangent—which are defined using the words hypotenuse, opposite, and adjacent. ... Side ratios in right triangles as a function of the angles.
Step-by-step explanation:
a whole number larger than $2$ leaves a remainder of $2$ when divided by each of the numbers $3$, $4$, $5$, and $6$. what is the smallest such number?
Answers
The smallest whole number larger than 2 which leaves the remainder as 2 when dividied by 3, 4, 5 and 6 is 62.
The Full form of LCM is Least Common Multiple. There are lots of methods of finding LCM of multiple numbers.
Now, finding the smallest number,
The LCM of 3, 4, 5, and 6 is 60.
So, the number of which leaves 2 as the remainder should be 60+2=62.
If we divide 62 by 3 the remainder is 2. If we divide 62 by 4, 5 and 6 the remainder is 2.
Hence, the smallest whole number larger than 2 which leaves the remainder as 2 when dividied by 3, 4, 5 and 6 is 62.
To learn more about LCM visit here:
https://brainly.com/question/233244
#SPJ4
Which represents a quadratic function?
f(x) = -8x3 - 16x2 - 4x
f(x) = 3/4 x2 + 2x - 5
f(x) = 4/x2 - 2/x + 1
f(x) = 0x2 - 9x + 7
Answers
please help!! the blank ones are the answer you can choose which one is correct.



Answers
Answer:
25 percent the answer is 25 percent I'm pretty sure. cause it's just 112.5/450
1.2. Tim bought 128 sandbags to completely fill a cube-shaped sandbox. Each bag fills a cubic foot in the sandbox. What is the length, in feet, of one of the sides of the sandbox?
A. √128
B. 3√128
c. 128^2
D. 128^3
Answers
Answer:
b
Step-by-step explanation:
Answer:
I think the answer is c.
Step-by-step explanation:
hope this helps
A garden that is 4 meters wide and 6 meters long is to have a uniform border such that the area of the border is the same as the area of the garden. Find the width of the border.
Answers
The width of the border is 1 meter.
How to find width of border?Let's assume that the width of the border is x meters. Then, the overall dimensions of the garden including the border would be (4 + 2x) meters by (6 + 2x) meters.
The area of the garden is:
Garden area = length x width = 6 x 4 = 24² meters
The area of the garden including the border is:
Total area = (6 + 2x) x (4 + 2x) = 24 + 20x + 4x²meters
We want the area of the border to be equal to the area of the garden, which means that:
Area of border = Total area - Garden area = 20x + 4x² meters
Since we want the area of the border to be equal to the area of the garden, we can set these two expressions equal to each other and solve for x:
20x + 4x² = 24
Dividing both sides by 4:
x² + 5x - 6 = 0
Factoring the quadratic:
(x + 6)(x - 1) = 0
The negative solution does not make sense for this problem, so we take the positive solution:
x = 1
Therefore, the width of the border is 1 meter.
Learn more about Width
brainly.com/question/26460797
#SPJ11
A nano-meter is 1 billionth of a metre. 12 Write this number as an ordinary decimal. The radius of a nitrogen atom is 1. 5 nano-metre. Q. 2 Radius Write this radius in metres using standard form
Answers
1 billionth of a meter is equivalent to 0.000000001 meters. The radius of a nitrogen atom, which is 1.5 nano-meters, can be expressed in standard form as 1.5 x 10^(-9) meters.
To convert 1 billionth of a meter into an ordinary decimal, we divide 1 by 1 billion, which gives us 0.000000001. This means that 1 billionth of a meter is equal to 0.000000001 meters.
To express the radius of a nitrogen atom, which is 1.5 nano-meters, in standard form, we first convert nano-meters to meters. Since 1 nano-meter is equal to 1 billionth of a meter, we can express 1.5 nano-meters as 1.5 x (1 billionth of a meter) = 1.5 x 0.000000001 meters.
In standard form, we express numbers in the form of a decimal multiplied by a power of 10. Since 0.000000001 can be written as 1 x 10^(-9), we have 1.5 x 10^(-9) meters as the standard form representation of the nitrogen atom's radius. This indicates that the radius of the nitrogen atom is 1.5 times 10 to the power of negative 9 meters.
Learn more about nano-meters here:
https://brainly.com/question/15883235
#SPJ11
What is the effect on the graph of the function f(x) = x2 when f(x) is changed to 7f(x)? A) stretched vertically B) compressed vertically stretched horizontally D) compressed horizontally
Answers
Answer:
It's D) compressed horizontally
how do i do this ?? help

Answers
Answer:
Find it in (m a t h w a y) that will give you the answers and explanation
If a given set of data has a variance of 64.58 and a sample size of 26, the the standard deviation is equivalent to
Answers
Standard deviation is a statistic that measures the dispersion of a dataset relative to its mean and is calculated as the square root of the variance.
Standard deviation = √ {(xi – x)^2 / (n-1)}
here (xi – x)^ 2 means variance and n is sample size .
so we can say
Standard deviation = √{ (variance / sample size – 1 )}
here variance is 64.58 and sample size is 26 is given.
So stand deviation = √{64.58 / (26-1)}
standard deviation =0.32144673
Know more about “standard deviation” here: https://brainly.com/question/28316289
#SPJ4
the standard deviation will be 0.32144673 for the data having variance as 64.58 and sample size as 26.
Standard deviation is a statistic that measures the dispersion of a dataset relative to its mean and is calculated as the square root of the variance.
Standard deviation = √ {(xi – x)^2 / (n-1)}
here (xi – x)^ 2 means variance and n is sample size .
so we can say
Standard deviation = √{ (variance / sample size – 1 )}
here variance is 64.58 and sample size is 26 is given.
So standard deviation = √{64.58 / (26-1)}
standard deviation = 0.32144673
Therefore, the standard deviation will be 0.32144673 for the data having variance as 64.58 and sample size as 26.
Learn more about “standard deviation” here: brainly.com/question/28316289
#SPJ4
What is the y-value of point A?

Answers
Answer: 1
The full term is (6,1)
Answer:
1
Step-by-step explanation:
Trust me on this, also can I have brainiest please?
Hope you do well! :D
Help help bell help math

Answers
Answer:
Should be 78
Step-by-step explanation:
use this formula C = 2radiuspi
26/2=13 radius
13*3=39
39*2=78
the circumfrence is 78.
Hope this helped, vote up and five stars!!!
Answer:
Answer:The circumference of this circle is 78.
Hope you could get an idea from here.
Doubt clarification - use comment section.
Hurry-?
What expression shows 3 less than a number?
A. n + 3
B. n - 3
C. 3 - n
D. 3n :)
Answers
The expression that shows "3 less than a number" is B. n - 3.
What are operations?Mathematical operations must be carried out in a specific order according to a set of rules known as the order of operations. The following is the order of events:
Operation inside brackets should come first. Expressions containing exponents should be evaluated next.
Division and Multiplication: Carry out division and multiplication from left to right. Addition and subtraction: Move from left to right when adding and subtracting. It is crucial to adhere to the order of operations since it guarantees accurate and consistent evaluation of mathematical expressions.
When we break the given phrase in to mathematical expression we have:
n - 3.
Hence, the expression that shows "3 less than a number" is B. n - 3.
Learn more about algebraic expression here:
https://brainly.com/question/28884894
#SPJ1
help plzzz i need someone to help me with this

Answers
Answer:
I think the answer to the question is C
Answer:
A
Step-by-step explanation:
The sign means that x is smaller than 3. There is no need for the line underneath since the dot is not filled in.
John and Mary had Php 384 altogether. After John gave Php 36 to Mary, Mary had 3 times as much money as John. How much money did Mary had at first?
Answers
John initially had Php 132 and Mary initially had Php 252 (384 - 132).
Let's start by setting up the equations to solve for this problem.
Let x be the amount of money John had initially.
Then, Mary had (384 - x) initially.
After John gave Php 36 to Mary, John had (x - 36) left and Mary had (384 - x + 36) = (420 - x).
We are told that Mary had three times as much money as John after this transaction, so we can write:
3(x - 36) = 420 - x
Simplifying this equation gives:
3x - 108 = 420 - x
4x = 528
x = 132
Therefore, John initially had Php 132 and Mary initially had Php 252 (384 - 132).
Answer: Mary had Php 252 at first.
Learn more about initially from
https://brainly.com/question/31041139
#SPJ11
the bottom-up approach to metrics yield the most easily obtainable metrics however many metrics collected in this approach may not be suitable for top-management. true or false
Answers
The statement ''The bottom-up approach to metrics yield the most easily obtainable metrics however many metrics collected in this approach may not be suitable for top-management.'' is true because the bottom-up approach to metrics focuses on collecting data and metrics at lower levels within an organization, such as individual departments or teams.
These metrics are typically more operational and task-oriented, providing detailed insights into specific areas of the business.
However, while the bottom-up approach yields easily obtainable metrics, many of these metrics may not be directly relevant or suitable for top-management decision-making.
Top management typically requires high-level, strategic metrics that align with organizational goals and provide a holistic view of performance.
To cater to the needs of top management, a top-down approach is often employed, which involves identifying key strategic metrics and aligning them with organizational objectives.
This approach ensures that the metrics collected are meaningful, actionable, and support informed decision-making at the executive level.
To know more about metrics refer here:
https://brainly.com/question/29317112#
#SPJ11
Triangle abc is represented. points d and f are marked on side ab and points e and g are marked on side ac. segments de and fg are drawn.
if , then line segment
is parallel to line segment
.
Answers
If points d and f are on side ab and points e ang g are on side ac then line segment de and fg are parallel.
Given There is a triangle abc.
Parallel lines are those lines that do not meet at any point. If we draw a triangle abc and plot points d and f are marked on side ab and points e and g are marked on side ac then the line segment fg is parallel to de because both the line segments are drawn from the points which are on the sides opposite to each other. We have assumed a simple triangle because no description is given for the triangle.
Hence the line segment fg is parallel to de if drawn points d and f marked on ab and points e and g are marked on ac.
Learn more about parallel lines here https://brainly.com/question/16742265
#SPJ10

Answer:D-E is parallel to FG which is parallel to B-C meaning all three are parallel
Step-by-step explanation:
A sample of 75 concrete blocks had a mean mass of 38.3 kg with a standard deviation of 0.6 kg.
a. How many blocks must be sampled so that a 95% confidence interval will specify the mean mass to within ±0.1 kg? (Round up the final answer to the nearest integer.)
The number of blocks that must be sampled is:
b. How many blocks must be sampled so that a 99% confidence interval will specify the mean mass to within ±0.1 kg? (Round up the final answer to the nearest integer.)
The number of blocks that must be sampled is:
Answers
For a 95% confidence interval, number of blocks that must be sampled is 139, and for a 99% confidence interval, number of blocks that must be sampled is 238.
We will use the formula for the sample size in a confidence interval estimation:
n = (Z * σ / E)²
Where n is the sample size, Z is the Z-score corresponding to the desired confidence level, σ is the standard deviation, and E is the margin of error.
a. For a 95% confidence interval, the Z-score is 1.96. The standard deviation is 0.6 kg, and the margin of error is ±0.1 kg. Plugging these values into the formula:
n = (1.96 * 0.6 / 0.1)²
n ≈ 138.3
Since we need to round up the final answer to the nearest integer, the number of blocks that must be sampled for a 95% confidence interval is 139.
b. For a 99% confidence interval, the Z-score is 2.576. Using the same formula with this new Z-score:
n = (2.576 * 0.6 / 0.1)²
n ≈ 237.8
Again, rounding up the final answer to the nearest integer, the number of blocks that must be sampled for a 99% confidence interval is 238.
In summary, for a 95% confidence interval, 139 blocks must be sampled, and for a 99% confidence interval, 238 blocks must be sampled.
Learn more about : Statistics - https://brainly.com/question/31426757
#SPJ11
What is the length of the hypotenuse of the triangle?
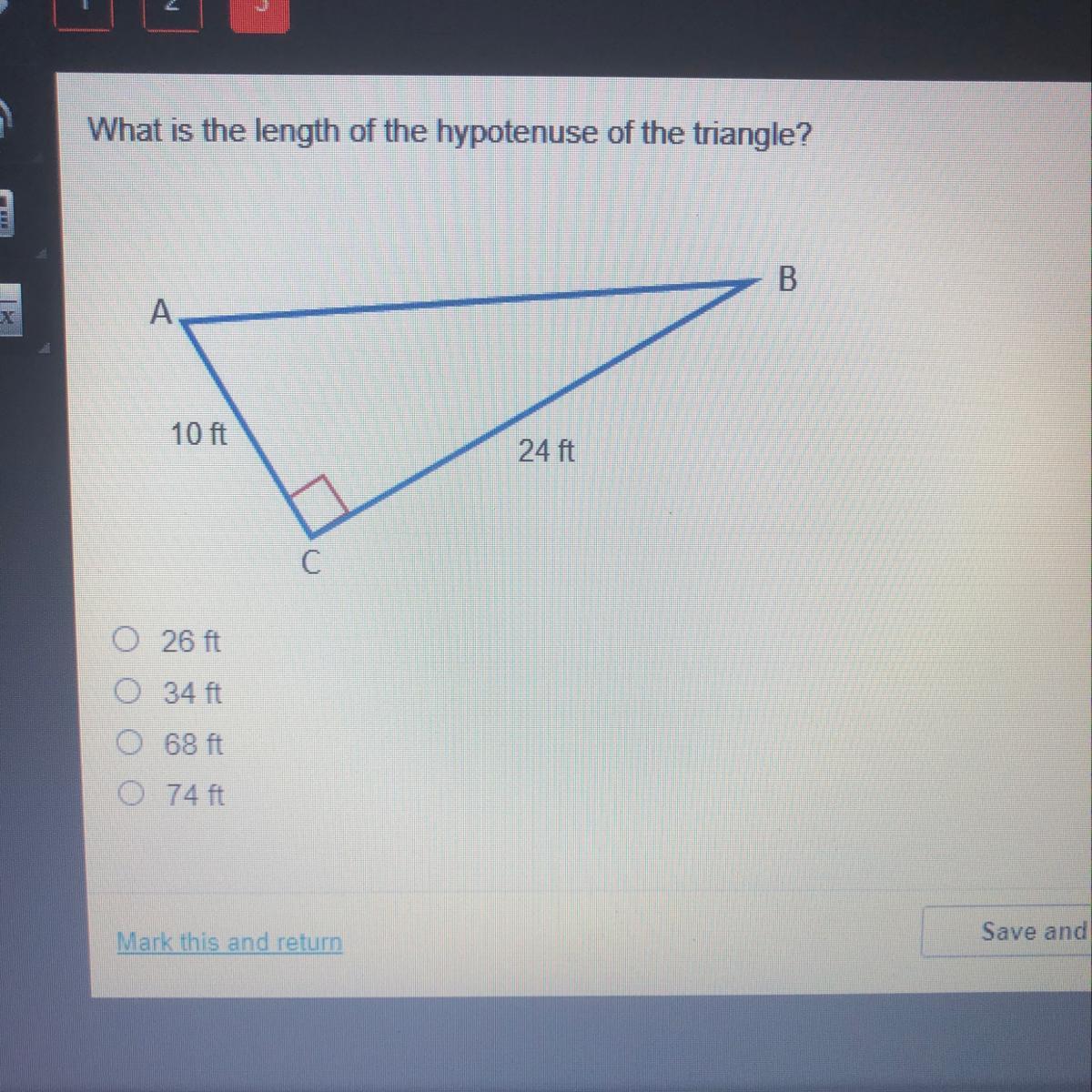
Answers
Answer:
26 ft
Step-by-step explanation:
Since this is a right triangle, we can use the Pythagorean theorem
a^2 + b^2 = c^2
10^2+24^2 = c^2
100 +576 = c^2
676 = c^2
Take the square root of each side
sqrt(676) = sqrt(c^2)
26 = c
Answer:
26 ft
Step-by-step explanation:
Pythagoras theorem
a^2+b^2=c^2
10^2+24^2=676
square root of 676= 26
What is the equation of the line parallel to the line -3y=-9x-15 and passing through the point (-4,-13)?
Answers
The equation of the line parallel to the line -3y = -9x - 15 and passing through the point (-4, -13) is y - 3x = 35
As per the given data: the line passes through the point (-4, -13) and is parallel to the line -3y = -9x - 15.
9x - 3y = 15
3x - y = 5
Here we have to determine the equation of the line that passes through the point (-4, -13) and is parallel to the line 3x - y = 5:
When two lines are parallel then their slopes are equal.
y = 3x - 5
Slope form - y = mx + c
Compare both the equations: m = 3
So, the slope of the line that passes through the point (-4, -13) is 3.
Using the one-point slope form of a line the equation of a line that passes through the point (-4, -13) and is parallel to the line 3x - y = 5 can be determined.
The one-point slope form is given below:
\(y - y_{1} = m(x-x_{1} )\)
Substitute the values of the known terms in the above equation.
y - (-4) = 3 (x - (-13))
y + 4 = 3 (x + 13)
y + 4 = 3x + 39
y - 3x = 39 - 4
y - 3x = 35
Therefore the required equation is y - 3x = 35
For more questions on slope
https://brainly.com/question/17709244
#SPJ4
Express the function y = 72 cos(wt) + 54 sin(wt) as a single sine wave y = A sin(wt + p) for some constants A and p. (a) The constant A = π π For part (b), express your answer in radians where <$< rounded to 3 decimal places. (b) The constant o = radians
Answers
y = 90 sin(wt + 2.498)Comparing it with y = A sin(wt + p), we getω = 1rad/s. Therefore, the constant ω is 1 radian.
Given function: y = 72 cos(wt) + 54 sin(wt)Rewriting it in the form of amplitude times sine of sum of angle and phase shift: y = A sin(wt + p) where A is amplitude and p is phase shift.A = √(72² + 54²) = √(5184 + 2916) = √(8100) = 90As sin is positive, so amplitude A is positive.θ = tan⁻¹(-54/72) = tan⁻¹(-3/4)In 2nd quadrant, sinθ is positive. Thus phase shift, p = π + θ = π + tan⁻¹(-3/4)π + tan⁻¹(-3/4) = 2.498 rad. Thus the required expression in a single sine wave is: y = 90 sin(wt + 2.498)Part (a) : The constant A = πWe have calculated the amplitude above, which is A = 90.π ≈ 3.142So, the constant A is approximately equal to 3.142 radians. Part (b) : The constant ω = ? Radians is the SI unit of angular frequency and is represented by ω.For the given equation: y = 90 sin(wt + 2.498), Comparing it with y = A sin(wt + p), we getω = 1rad/s, Therefore, the constant ω is 1 radian.
To know more about phase visit:
https://brainly.com/question/32044786
#SPJ11
.(a) describe the type of indeterminate form (if any) that is obtained by direct substitution. (b) Evaluate the limit, using LâHôpitalâs Rule if necessary. (c) Use a graphing utility to graph the function and verify the result in part (b). lim_(xâ0^+) [cos(Ï/2 - x)]^x
Answers
The type of indeterminate form obtained by direct substitution in the given limit is 1^∞, where 1^∞ is not a determinate form and its value is not always predictable.
Applying L'Hôpital's Rule to the limit, we get:
lim_(xâ0^+) [cos(Ï/2 - x)]^x = lim_(xâ0^+) e^[x ln(cos(Ï/2 - x))]
Now, applying L'Hôpital's Rule to the exponent, we get:
= lim_(xâ0^+) e^[x (-tan(Ï/2 - x))]
= e^0 = 1
Therefore, the limit is equal to 1.
Using a graphing utility to graph the function, we can see that the limit approaches 1 as x approaches 0 from the right side. Therefore, the result obtained using L'Hôpital's Rule is verified by the graph.
To learn more about indeterminate : brainly.com/question/30633788
#SPJ11
A sprinter ran 100 meters in 15 seconds.
What was his rate in meters per minute?
Enter your answer in the box.
Answers
Answer:
The sprinter's rate in meters per minute is 400 or 400 meters per minute
Step-by-step explanation:
hope this helps!
if not i am sorry
Answer:
400
Step-by-step explanation:
k12
60 / 15 = 4
4 x 100 = 400
The ratio of lions to tigers is
Answers
Emma spent $29. 00 on average for each of the 3 times Emma went to eat at restaurants. By eating at home, it would have averaged just $8. 00 a meal. How much more did Emma need to budget for eating at restaurants instead of eating at home?
Answers
Emma needed to budget an extra $87.00 - $24.00 = $63.00 for eating at restaurants instead of eating at home.
What is the equivalent expression?
Equivalent expressions are expressions that perform the same function despite their appearance. If two algebraic expressions are equivalent, they have the same value when we use the same variable value.
Emma spent a total of $29.00 x 3 = $87.00 on eating at restaurants.
If Emma had eaten at home, she would have spent $8.00 x 3 = $24.00.
Therefore, Emma needed to budget an extra $87.00 - $24.00 = $63.00 for eating at restaurants instead of eating at home.
To learn more about the equivalent expression visit:
https://brainly.com/question/2972832
#SPJ4
Please help I am confused.

Answers
Answer:
y = 15° , ∠BAC = 78° , ∠ABC = 68° , ∠ACB = 34°
Step-by-step explanation:
we can find ∠ACB as it lies on a straight line,
∠ACB + 146 = 180°
∠ACB = 180° - 146°
∠ACB = 34°
We know that all sides of triangle equals to 180°
so,
∠BAC + ∠ABC + ∠ACB = 180°
5y + 3 + 4y + 8 + 34 = 180°
9y + 45° = 180°
9y = 135°
y = 15°
So know we can find angles =
∠BAC = 5y + 3 = 5(15) + 3 = 78°
∠ABC = 4y + 8 = 4(15) + 8 = 68°
we already know that ∠ACB = 34°
