Answers
Related Questions
help me please it’s urgent how do i solve this I was absent

Answers
Hi!
I can help you, no worries!
Your answer is y = -4/5x - 3
To solve this is much easier than you think. To "solve for y" we just have to get y on one side of the equal sign all by itself. We can see that it's "1 + y" on the left instead of just the y.
To get y by itself, we just subtract "1" from both sides.
1 + y = -4/5x - 2
-1 -1
y = -4/5x - 3
If you don't know why we have to subtract from both sides, think of it like this (it's how I like to think of it).
Each side of the equal sign is a twin. They are equal to eachother. If you change something about one twin, such as changing their hair color (or adding a number to one side of the equal sign), you have to do it to both in order for them to be the same. Right?
Hope this helps! Have a great day! :D
the point (-12,5) lies on the circle whose center is at the origin. what is the radius of this circle?
Answers
The radius of the circle is 13.
To find the radius of the circle with the center at the origin and passing through the point (-12, 5), we can use the distance formula.
The distance formula between two points (x1, y1) and (x2, y2) is given by:
Distance = √[(x2 - x1)² + (y2 - y1)²]
In this case, the center of the circle is at the origin (0, 0), and the given point is (-12, 5). Plugging these values into the distance formula, we get:
Distance = √[(-12 - 0)² + (5 - 0)²]
= √[(-12)² + 5²]
= √[144 + 25]
= √169
= 13
Know more about circle here:
https://brainly.com/question/12930236
#SPJ11
ezra determined that the graph shown below is vertically compressed by a factor of 1/3 from the graph of y=|x| do you agree or disagree? why?
Answers
Answer:
Step-by-step explanation:
no graph was shown
A wildlife manager determines that there are approximately 800 deer in a state park. The population is decreasing at a rate of 5% each year. How many deer would you expect to live in the park after 5 years? Round to the nearest whole
Answers
Step-by-step explanation:
5 % decrease means 95 % (.95) remain
Year 1
800 * .95
year 2 800 * .95 * .95
.
.
year 5 = 800(.95)^5 = 619 deer after year 5
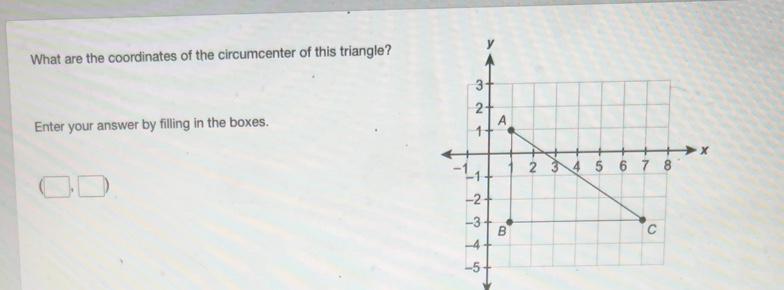
What are the coordinates of the circumcenter of this triangle?
Enter your answer by filling in the boxes.
Answers
The coordinates of the circumcenter of the triangle ΔABC is; ( 4 , -1 )
What is the circumcenter of a triangle?The circumcenter of a triangle is the point of intersection of the perpendicular bisectors of the triangle, therefore;
The coordinates of the centers of the sides of the triangle are; ((1+7)/2, (1 + (-3))/2)
((1+7)/2, (1 + (-3))/2) = (4, -1)
The equation of the side AB is; y - 1 = ((1 - (-3))/(1 - 7))·(x - 1) = (-2/3)·(x - 1)
y = (-2/3)·(x - 1) + 1
y = (-2/3)·(x - 1) + 1
The equation of the perpendicular bisector of AB is; y - (-1) = (3/2)·(x - 4)
y + 1 = (3/2)·(x - 4)
y = (3/2)·(x - 4) - 1 = 3·x/2 - 7
y = 3·x/2 - 7
The middle of the side AB is; ((1 + 1)/2, (1 + (-3))/2) = (0, -1)
The side AB is vertical, therefore, the slope of the perpendicular line to AB is 0, and the equation of the perpendicular bisector to AB therefore is; y = -1
The x-coordinates of the circumcenter can therefore be found as follows;
-1 = 3·x/2 - 7
3·x/2 - 7 = -1
3·x/2 = -1 + 7 = 6
x = (2/3) × 6 = 4
x = 4
The y-coordinate of the circumcenter is; y = -1
The coordinate of the circumcenter of the circle is; (4, -1)Learn more on the circumcenter of a circle here: https://brainly.com/question/29630712
#SPJ1
Thor was playing a game in which he gained and lost points. First, he
lost nine points two times. Next, he earned two points. After that, he
earned nine points four times. Last, he lost eleven points four times.
Write the total change to his score as an integer.
Answers
Answer:
-24
Step-by-step explanation:
assume the point (10,20) belongs to the graph of f of x what point belongs to the graph of y equals f (x )minus 5
Answers
assume the point (10,20) belongs to the graph of f of x what point belongs to the graph of y equals f (x )minus 5
In this problem we have a transformation with the dollowing rule
(x,y) ------> (x,y-5)
so
(10,20) --------> (10, 20-5)
(10,20) --------> (10, 15)
therefore
The answer is
(10, 15)
On a postsynaptic membrane, the opening of which ion channel(s) induces an IPSP? Why? VRest -70 mV, threshold = -55 mV, Ec= -63 mV, Ex = -90 mV, and ENa = 60 mV. a) K+; It hyperpolarizes the neuron. O
Answers
On a postsynaptic membrane, the opening of K+ ion channel induces an IPSP (Inhibitory Postsynaptic Potential).
The potential changes in a neuron after the receptor and ion channel activation is called synaptic potential. This potential can be either an Excitatory Postsynaptic Potential (EPSP) or an Inhibitory Postsynaptic Potential (IPSP).EPSP is a depolarizing potential that results from the opening of the Na+ ion channel. It causes a change in the potential of the neuron towards threshold level that may trigger an action potential.Ion channels and pumps in a postsynaptic neuron regulate the internal potential of the cell. In a typical postsynaptic cell, the resting potential (Vrest) is -70 mV, the threshold value is -55 mV, the reversal potential for Cl- ion (Ec) is -63 mV, the reversal potential for K+ ion (Ex) is -90 mV, and the reversal potential for Na+ ion (ENa) is 60 mV.The opening of Cl- ion channel leads to an inward flow of negative ions and thus results in hyperpolarization. The opening of K+ ion channel leads to an outward flow of K+ ions, and the membrane potential becomes more negative. Thus, it also results in hyperpolarization. The opening of a Na+ ion channel leads to inward flow of Na+ ions, which makes the cell more positive, and it is depolarization. Therefore, the opening of K+ ion channel leads to an IPSP, and it hyperpolarizes the neuron.
The postsynaptic potential can be either an Excitatory Postsynaptic Potential (EPSP) or an Inhibitory Postsynaptic Potential (IPSP). The opening of the K+ ion channel leads to an outward flow of K+ ions, which makes the cell more negative and hyperpolarizes it, leading to IPSP.
To learn more about postsynaptic membrane visit:
brainly.com/question/14969022
#SPJ11
I really need help it's due today at 2:00
1.Find the value of f(–9) and g(1) if f(x) = 8x + 6 and g(x) = 9x + 20x−2
A.f(–9) = 14
g(1) = 30
B.f(–9) = –78
g(1) = –11
C.f(–9) = –66
g(1) = 29
D.f(–9) = 8
g(1) = –80.75
2.Find the value of f(–9) and g(–1) if f(x) = –3x – 2 and g(x) = 3x3 – 24x .
A. f(–9) = 25
g(–1) = 21
B.f(–9) = –5
g(–1) = 20
C.f(–9) = 29
g(–1) = 26
D.f(–9) = 3
g(–1) = –27
Answers
Answer:
1. f(–9) = -66 , g( 1 ) = 27 (Please double-check your given options, there must have been a typographical error for Option C for g( 1 ) = 29). g( 1 ) is supposed to be 27.
2. Option A: f(–9) = 25, g(–1) = 21
Step-by-step explanation:
1.Find the value of f(–9) and g(1) if f(x) = 8x + 6 and g(x) = 9x + 20x−2
f(x) = 8x + 6
f(–9) = 8(-9) + 6 = -66
g(x) = 9x + 20x − 2
g( 1 ) = 9( 1 ) + 20( 1 ) − 2 = 27
None of the given choices were correct (unless there's a typo error for Option C — it's supposed to be g( 1 ) = 27 instead of 29?) because the correct answers are: f(–9) = -66 and g( 1 ) = 27
2. f(–9) and g(–1) if f(x) = –3x – 2 and g(x) = 3x³ – 24x
f(x) = –3x – 2
f(–9) = –3(–9) – 2 = 25
g(x) = 3x³ – 24x
g(–1) = 3(–1)³ – 24(–1) = 21
Therefore, the correct answer is Option A: f(–9) = 25, g(–1) = 21
A cone has a circular base of radius 13.5 m. Given that the total surface area of the cone is 1240 m^2, find it's volume.
I'meaving brainly, just answer the question and take pointsss...
Answers
Answer:
1543.59
Step-by-step explanation:
See image below for equation!
PLZZZ give me brainliest!

Write the linear equation in slope-intercept form from the description. Use c to represent the total cost and m to represent the number of movie rentals. The cost of a movie streaming service is $8.50, plus $1.50 per movie rental.
Please Help me
Answers
A linear equation in slope-intercept form that models the description is c = 1.50m + 8.50.
What is the slope-intercept form?Mathematically, the slope-intercept form of the equation of a straight line is given by this mathematical expression;
y = mx + c
Where:
m represents the slope or rate of change.x and y are the points.c represents the y-intercept or initial value.Assuming the variable c represent the total cost and the variable m to represent the number of movie rentals, a linear equation in slope-intercept form that models the scenario is given by:
c = 1.50m + 8.50.
Read more on slope here: brainly.com/question/3493733
#SPJ1
Ana vai fazer pulseiras de miçangas para presentear alguns amigos. para fazer cada uma dessas pulseiras, ela precisa de 16 miçangas. ana tem 4 potes com quantidades diferentes de miçangas e quer escolher, para utilizar na confecção dessas pulseiras, aquele que tem uma quantidade de miçangas que permite fazer uma determinada quantidade de pulseiras sem sobrar nenhuma miçanga no pote. observe, no quadro abaixo, as quantidades de miçangas disponíveis em cada um dos potes que ana tem.
Answers
Para escolher o pote de miçangas que permitirá fazer uma quantidade exata de pulseiras sem sobrar nenhuma miçanga no pote, precisamos encontrar um número que seja divisível por 16 em cada um dos valores apresentados nos potes.
Analisando as opções apresentadas no quadro, podemos ver que apenas a quantidade de miçangas no pote B é divisível por 16, já que 16 x 9 = 144. Portanto, Ana deve escolher o pote B com 144 miçangas para confeccionar as pulseiras de seus amigos. Dessa forma, ela poderá fazer 9 pulseiras utilizando todas as miçangas disponíveis no pote. As outras opções apresentam quantidades de miçangas que não são divisíveis por 16, o que resultaria em sobras de miçangas no processo de confecção das pulseiras.
Learn more about escolher here
https://brainly.com/question/16607567
#SPJ11
A satellite dish is being designed so that it can pick up radio waves coming from space. The satellite dish will be in the shape of a parabola and will be positioned above the ground such that its focus is 30 ft above the ground. Using the ground as the x-axis, where should the base of the satellite be positioned? Which equation best describes the equation of the satellite?
(0, 60); y = one over two hundred fortyx2 + 60
(0, 15); y = one over sixtyx2 + 15
(0, 60); y = one over two hundred fortyx2 − 60
(0, 15); y = one over sixtyx2 − 15
Answers
Step-by-step explanation:
The shape of a parabola is determined by its focus and directrix. In this problem, the focus is 30 ft above the ground, so the directrix is 30 ft below the ground. Since the ground is the x-axis, the directrix is a horizontal line with equation y = -30.
The base of the satellite dish should be positioned on the axis of symmetry of the parabola, which passes through the focus and is perpendicular to the directrix. Since the directrix is a horizontal line, the axis of symmetry is a vertical line passing through the focus. Therefore, the base of the satellite dish should be positioned directly below the focus, which is (0, 30).
The equation of a parabola with vertex at the origin, opening upwards or downwards, and axis of symmetry along the y-axis is given by the equation y = a x^2, where a is a constant. In this problem, the parabola opens upwards and its vertex is (0, 30), so the equation of the parabola is of the form y = a x^2 + 30.
To determine the value of a, we need to use the fact that the directrix is y = -30. The distance from a point (x, y) on the parabola to the directrix is given by |y - (-30)| = |y + 30|. The distance from the same point to the focus (0, 30) is given by the distance formula:
sqrt(x^2 + (y - 30)^2)
Since the point lies on the parabola, we can substitute y = ax^2 + 30 into this expression and simplify:
sqrt(x^2 + (a x^2)^2) = sqrt(1 + a^2) x^2
Now we can set the two expressions for the distances equal to each other and solve for a:
|ax^2 + 30 + 30| = sqrt(1 + a^2) x^2
|ax^2 + 60| = sqrt(1 + a^2) x^2
a^2 x^4 + 120 a x^2 + 3600 = x^4 + a^2 x^4
(a^2 - 1) x^4 + 120 a x^2 + 3600 = 0
This is a quartic equation in x^2. We can solve for x^2 using the quadratic formula:
x^2 = (-120 a ± sqrt(120^2 a^2 - 4 (a^2 - 1) 3600)) / 2(a^2 - 1)
x^2 = (-60 a ± sqrt(3600 a^2 + 14400)) / (a^2 - 1)
For the base of the satellite dish to be positioned on the ground, we need x^2 to be non-negative, which means the discriminant of the quadratic formula must be non-negative:
3600 a^2 + 14400 ≥ 0
a^2 ≥ -4
Since a is a positive constant that determines the shape of the parabola, we can take the positive square root of both sides and obtain a ≥ 0. Therefore, the equation of the satellite is:
y = a x^2 + 30, where a is a non-negative constant.
None of the provided equations match the answer obtained.
What is the maximum speed of the sprinter during the race?

Answers
The maximum speed of the sprinter during the race is estimated to be approximately 12.72 meters per second.
To calculate the maximum speed of the sprinter during the race, we need to determine the average speed over the entire distance. The formula for average speed is distance divided by time. In this case, the distance covered by the sprinter is 200 meters, and the time taken to cover this distance is 20.32 seconds.
Average Speed = Distance / Time
Average Speed = 200 meters / 20.32 seconds
Average Speed ≈ 9.84 meters per second
So, the average speed of the sprinter during the race is approximately 9.84 meters per second.
However, to find the maximum speed, we need to consider that sprinters often accelerate during a race. The sprinter's time splits of 0-5-20.32 indicate that it took the sprinter 5 seconds to cover the initial 0 meters. This suggests that the sprinter was accelerating during this period.
To estimate the maximum speed, we can calculate the average speed for the remaining 195 meters (200 meters - 5 meters).
Average Speed = Distance / Time
Average Speed = 195 meters / (20.32 seconds - 5 seconds)
Average Speed ≈ 195 meters / 15.32 seconds
Average Speed ≈ 12.72 meters per second
Therefore, the maximum speed of the sprinter during the race is estimated to be approximately 12.72 meters per second. It's important to note that this is an estimate based on the given information, and actual maximum speeds achieved by athletes can vary based on various factors such as training, technique, and race conditions.
For more such questions on average speed
https://brainly.com/question/13318003
#SPJ8
if 7(n-m) = 3m, what is m/n
Answers
Answer:
10m/7n
Step-by-step explanation:
distribute the
7n-7m=3m
7n=
AC is a diameter of OE, the area of the
circle is 289 units2, and AB = 16 units.
Find BC and mBC.
B
A
C
E. plssss hurry !!

Answers
The measure of arc BC is 720 times the measure of angle BAC.
Given that AC is the diameter of the circle and AB is a chord with a length of 16 units, we need to find BC (the length of the other chord) and mBC (the measure of angle BAC).
To find BC, we can use the property of chords in a circle. If two chords intersect within a circle, the products of their segments are equal. In this case, since AB = BC = 16 units, the product of their segments will be:
AB * BC = AC * CE
16 * BC = 2 * r * CE (AC is the diameter, so its length is twice the radius)
Since the area of the circle is given as 289 square units, we can find the radius (r) using the formula for the area of a circle:
Area = π * r^2
289 = π * r^2
r^2 = 289 / π
r = √(289 / π)
Now, we can substitute the known values into the equation for the product of the segments:
16 * BC = 2 * √(289 / π) * CEBC = (√(289 / π) * CE) / 8
To find mBC, we can use the properties of angles in a circle. The angle subtended by an arc at the center of a circle is double the angle subtended by the same arc at any point on the circumference. Since AC is a diameter, angle BAC is a right angle. Therefore, mBC will be half the measure of the arc BC.
mBC = 0.5 * m(arc BC)
To find the measure of the arc BC, we need to find its length. The length of an arc is determined by the ratio of the arc angle to the total angle of the circle (360 degrees). Since mBC is half the arc angle, we can write:
arc BC = (mBC / 0.5) * 360
arc BC = 720 * mBC
Therefore, the length of the arc BC equals 720 times the length of the angle BAC.
for such more question on measure of arc
https://brainly.com/question/25716982
#SPJ8
Rewrite the perimeter formula, P = 2/ + 2w, to solve for the length, I, and then
use this formula to find the length of a rectangle whose width is 7 inches and
perimeter is 42 inches.
Answers
P = 2l + 2w
Subtract both sides by 2w
P - 2w = 2l
Divide both sides by 2
(P - 2w) / 2 = l
In our problem,
w = 7 in
P = 42 in
Let's plug our values into the formula above.
(42 in - 2(7 in) / 2 = l
(42 in - 14 in) / 2 = l
28 / 2 = l
14 in = length
HCSS has a goal to answer all technical support calls by the third ring, or within 21 seconds. If on Monday we answered 500 calls before noon with an average answer time of 16 seconds, 350 calls from noon to 6pm in an average of 14 seconds, and 150 calls on Monday night with an average time of 20 seconds, what was our average answer time for the entire day on Monday
Answers
The average answer time for the entire day on Monday was 15.9 seconds.
For the average answer time for the entire day on Monday, we need to calculate the total time spent answering calls and divide by the total number of calls answered.
Let's first calculate the total time spent answering calls:
- For the 500 calls before noon, the total time spent answering calls is: 500 x 16 = 8,000 seconds
- For the 350 calls from noon to 6pm, the total time spent answering calls is: 350 x 14 = 4,900 seconds
- For the 150 calls on Monday night, the total time spent answering calls is: 150 x 20 = 3,000 seconds
So the total time spent answering calls on Monday is:
8,000 + 4,900 + 3,000 = 15,900 seconds
Now, let's calculate the total number of calls answered:
500 + 350 + 150 = 1,000 calls
Finally, we can calculate the average answer time for the entire day on Monday:
Average answer time = Total time spent answering calls / Total number of calls answered
= 15,900 / 1,000
= 15.9 seconds
Therefore, the average answer time for the entire day on Monday was 15.9 seconds.
To know more about averages refer here :
https://brainly.com/question/31337778#
#SPJ11
Two dice are tossed. Let X be the absolute difference in the number of dots facing up. (a) Find and plot the PMF of X. (b) Find the probability that X lessthanorequalto 2. (c) Find E[X] and Var[X].
Answers
a. the probabilities for X = 3, X = 4, and X = 5. The PMF of X can be plotted as a bar graph, with X on the x-axis and P(X) on the y-axis. b. Var[X] = E[X^2] - (E[X])^2
(a) To find the PMF (Probability Mass Function) of X, we need to consider all possible outcomes when two dice are tossed. There are 36 possible outcomes, each of which has a probability of 1/36. The absolute difference in the number of dots facing up can be 0, 1, 2, 3, 4, 5. We can calculate the probabilities of these outcomes as follows:
When the absolute difference is 0, the numbers on both dice are the same, so there are 6 possible outcomes: (1,1), (2,2), (3,3), (4,4), (5,5), and (6,6). The probability of each outcome is 1/36. Therefore, P(X = 0) = 6/36 = 1/6.
When the absolute difference is 1, the numbers on the dice differ by 1, so there are 10 possible outcomes: (1,2), (2,1), (2,3), (3,2), (3,4), (4,3), (4,5), (5,4), (5,6), and (6,5). The probability of each outcome is 1/36. Therefore, P(X = 1) = 10/36 = 5/18.
When the absolute difference is 2, the numbers on the dice differ by 2, so there are 8 possible outcomes: (1,3), (3,1), (2,4), (4,2), (3,5), (5,3), (4,6), and (6,4). The probability of each outcome is 1/36. Therefore, P(X = 2) = 8/36 = 2/9.
Similarly, we can find the probabilities for X = 3, X = 4, and X = 5. The PMF of X can be plotted as a bar graph, with X on the x-axis and P(X) on the y-axis.
(b) To find the probability that X ≤ 2, we need to add the probabilities of X = 0, X = 1, and X = 2. Therefore, P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2) = 1/6 + 5/18 + 2/9 = 11/18.
(c) To find the expected value E[X], we can use the formula E[X] = ∑x P(X = x). Using the PMF values calculated in part (a), we get:
E[X] = 0(1/6) + 1(5/18) + 2(2/9) + 3(1/6) + 4(1/18) + 5(1/36)
= 35/12
To find the variance Var[X], we can use the formula Var[X] = E[X^2] - (E[X])^2, where E[X^2] = ∑x (x^2) P(X = x). Using the PMF values calculated in part (a), we get:
E[X^2] = 0^2(1/6) + 1^2(5/18) + 2^2(2/9) + 3^2(1/6) + 4^2(1/18) + 5^2(1/36)
= 161/18
Therefore, Var[X] = E[X^2] - (E[X])^2
Learn more about probabilities here
https://brainly.com/question/25839839
#SPJ11
An ice cream shop sells 2 scoops of ice cream for $6. What would be the cost for 9 scoops of ice cream?
Answers
Answer: 27
Step-by-step explanation:
If 2 scoops of ice cream cost $6, then 1 scoop of ice cream costs $6/2 = $3.
So, 9 scoops of ice cream would cost 9 x $3 = $27.
Answer:
27$
Step-by-step explanation:
If two wcoops of ice crewm cost 6$ them one scoop would cost 3$ because 6/2 =3. If one scoop costs 3$ then 9 scoops would cost 9x3 so 27$
Make a box-and-whisker plot for each set of values. 20,23,25,36,37,38,39,50,52,55
Answers
The vertical lines (whiskers) extend from the box to the minimum value (20) and the maximum value (55).
That's how you create a box-and-whisker plot for the given set of values.
To create a box-and-whisker plot for the given set of values: 20, 23, 25, 36, 37, 38, 39, 50, 52, 55, you need to follow these steps:
Step 1: Sort the data in ascending order:
20, 23, 25, 36, 37, 38, 39, 50, 52, 55
Step 2: Find the median (middle value):
Since we have 10 data points, the median is the average of the two middle values. In this case, the two middle values are 37 and 38. So, the median is (37 + 38) / 2 = 37.5.
Step 3: Determine the lower quartile (Q1):
The lower quartile is the median of the lower half of the data set. In our case, the lower half is:
20, 23, 25, 36, 37
Since we have an odd number of values, the lower quartile Q1 is the median of this subset. The median of this subset is 25.
Step 4: Determine the upper quartile (Q3):
The upper quartile is the median of the upper half of the data set. In our case, the upper half is:
38, 39, 50, 52, 55
Again, since we have an odd number of values, the upper quartile Q3 is the median of this subset. The median of this subset is 50.
Step 5: Find the minimum and maximum values:
The minimum value from the sorted list is 20, and the maximum value is 55.
Step 6: Plot the box-and-whisker plot:
Now that we have all the necessary values, we can create the box-and-whisker plot:
| |
-----|-----------|-----
20 | | |
|---|-------|
| |
25 | |
|-----------|
37 | |
|-----------|
| |
50 | |
|---|-------|
| | |
55 | |
| |
In the plot:
The line in the middle represents the median (37.5).
The box represents the interquartile range (IQR), which spans from the lower quartile (Q1 = 25) to the upper quartile (Q3 = 50).
The vertical lines (whiskers) extend from the box to the minimum value (20) and the maximum value (55).
That's how you create a box-and-whisker plot for the given set of values.
Learn more about value from
https://brainly.com/question/24078844
#SPJ11
Find range of the real function
\(f = \left \{ \bigg(x, \: \dfrac{ {x}^{2} }{ {x}^{2} + 1} \bigg) : x \: \in \: R \right \}\)
from R into R.
Answers
Step-by-step explanation:
\( \large\underline{\sf{Solution-}}\)
Given function is
\(\rm \longmapsto\:f = \bigg(x, \: \dfrac{ {x}^{2} }{ {x}^{2} + 1} \bigg) : x \: \in \: R\)
To find the range of the function f, Let assume that
\(\rm \longmapsto\:y = \dfrac{ {x}^{2} }{ {x}^{2} + 1} \)
\(\rm \longmapsto\: {yx}^{2} + y = {x}^{2} \)
\(\rm \longmapsto\: {yx}^{2} - {x}^{2} = - y\)
\(\rm \longmapsto\: - {x}^{2} (1 - y) = - y\)
\(\rm \longmapsto\: {x}^{2} (1 - y) = y\)
\(\rm \longmapsto\: {x}^{2} = \dfrac{y}{1 - y} \)
\(\rm\implies \:x = \sqrt{\dfrac{y}{1 - y} } \)
For x to be defined,
\(\rm \longmapsto\:y \geqslant 0 \: \: and \: \: 1 - y > 0\)
\(\rm \longmapsto\:y \geqslant 0 \: \: and \: \: - y > - 1\)
\(\rm \longmapsto\:y \geqslant 0 \: \: and \: \: y < 1\)
\(\bf\implies \:y \: \in \: [0, \: 1)\)
Hence,
\(\bf\implies \:Range \: of \: f \: \in \: [0, \: 1)\)
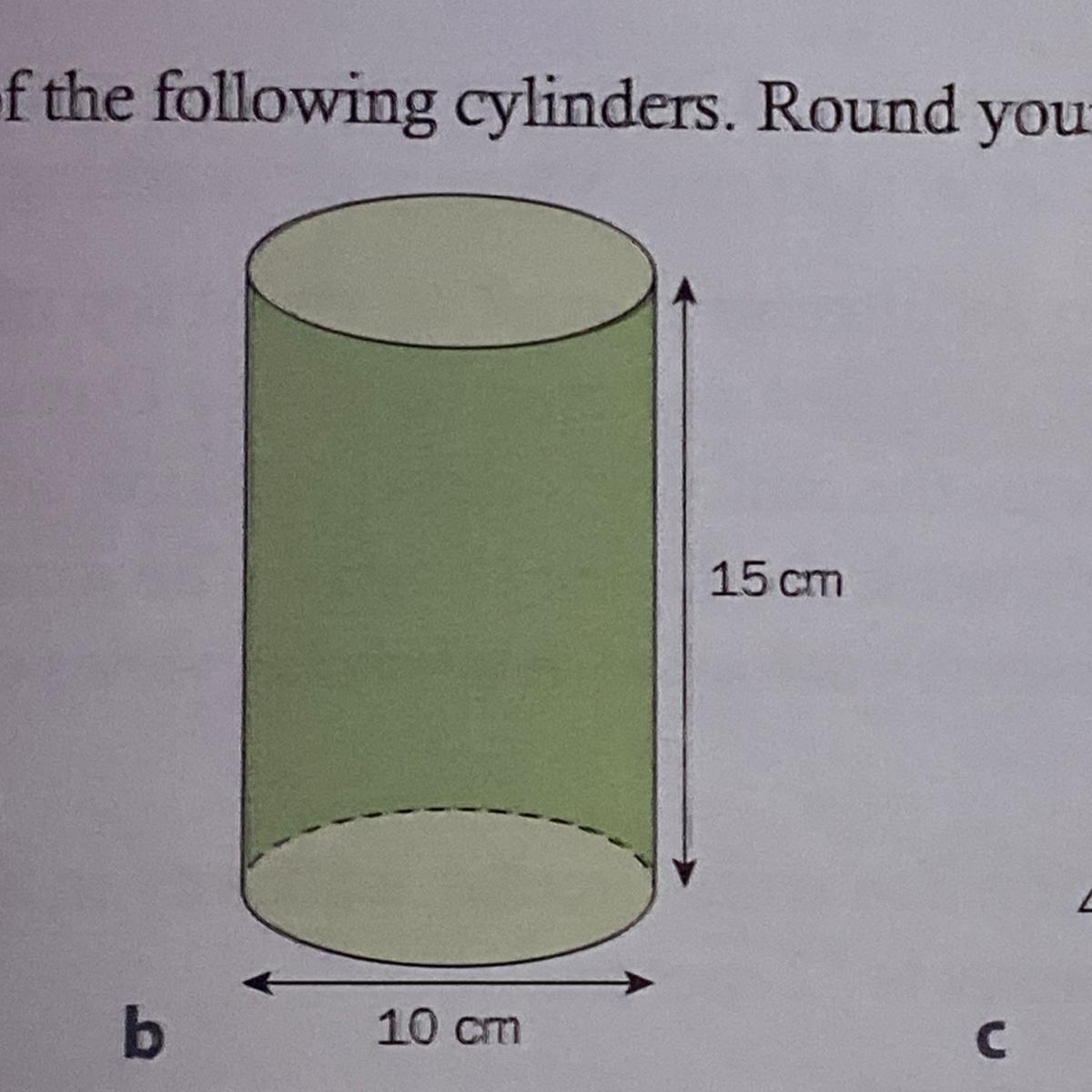
Find the surface area of the following cylinder. Round your answers to the nearest tenth.
Answers
Answer: 628
Step-by-step explanation:
2πr^2+2πrh
2(3.14)(5)^2+2(3.14)(5)(15)
2(3.14)(25)+2(3.14)(75)
2(78.5)+2(235.5)
157+471
628
In 1992, Jason bought a gallon of gas for $1.20. Yesterday, he bought a gallon of gas for $2.17. What is the percentage increase of the price of a gallon of gas from 1992 to yesterday? If necessary, round to the nearest tenth of a percent.
Answers
The percentage increase in the price of a gallon of gas is 80.84 %.
Given,
Jason bought a gallon of gas in 1992 = $1.20
He bought a gallon of gas yesterday = $2.17
Using the formula for the percentage increase in the price,
= ( New Price - Old Price) / Old Price × 100
= ( 2.17 - 1.20) / 1.20 × 100
= 80.84%
Therefore, the percentage increase in the price of a gallon of gas from 1992 to yesterday is 80.84 %.
A similar question was answered here,
brainly.com/question/11839495
Solve for r.
55°
6x + 1
Answers
Answer:
.6r + 1 = 556r = 55-16r = 54divide 6 both sides.r = 9What is the solution to this system of equations?

Answers
Find all values of x in the interval [0, 2] that satisfy the equation. (enter your answers as a comma-separated list.) 5 sin(2x) = 5 cos(x)
Answers
All values of x in the interval [0, 2] that satisfy the equation are \(\frac{\pi }{2} ,3\frac{\pi }{2}\).
What is an equation?A mathematical equation is a formula that uses the equals symbol (=) to connect two expressions and express their equality. A well-formed formula consisting of two expressions linked by an equals sign is considered to be an equation in English, but the word's cognates in other languages may have slightly different definitions. For instance, an équation is defined as having one or more variables in French.
The first step in resolving a variable equation is to identify the values of the variables that lead to the equality being true. The variables that must be changed in order to solve the equation are referred to as the unknowns, and the values of the unknowns that satisfy the equality are referred to as the equation's solutions.
Calculations:
16cos(x +8sin(2x)=0
Divide by 8
2cos(x)+sin(2x)=0
Identity:
sin(2x)=2sin(x)cos(x)
2cos(x)+2sin(x)cos(x)=0
Factor:
2cos(x)(1+sin(x))=0
2cos(x)=0
cos(x)=0=x=\(\frac{\pi }{2}\),3\(\frac{\pi }{2}\)
(1+sin(x))=0
sin(x)=−1=x=3\(\frac{\pi }{2}\)
To learn more about equation , visit:
https://brainly.com/question/10413253
#SPJ4
the magnification of a convex mirror is 0.67 times for objects 3.8 m from the mirror. What is the focal length of this mirror?
Answers
Magnification of a convex mirror is 0.67 times for objects 3.8 m from the mirror .the focal length is negative, this means that the mirror is a diverging mirror (convex mirror). Therefore, the focal length of this mirror is 2.4 meters.
To find the focal length of a convex mirror, we can use the mirror formula:
1/f = 1/v + 1/u
where f is the focal length, v is the image distance, and u is the object distance.
In this case, we know that the magnification (M) of the mirror is 0.67, and the object distance (u) is 3.8 m. We also know that for a convex mirror, the image is always virtual and upright, so the image distance (v) is negative.
The magnification formula is:
M = -v/u
Substituting the values we have:
0.67 = -v/3.8
v = -2.546 m
Now we can use the mirror formula to find the focal length:
1/f = 1/-2.546 + 1/3.8
1/f = -0.416
f = -2.4 m
Since the focal length is negative, this means that the mirror is a diverging mirror (convex mirror). Therefore, the focal length of this mirror is 2.4 meters.
To know more about Magnification visit :
https://brainly.com/question/20368024
#SPJ11
A continuous random variable x is uniformly distributed on the interval [35, 45]. the probability that x is between 40 and 50 is:________
Answers
The probability that x is between 40 and 50 will be 0.5.
How to illustrate the probability?From the information, the continuous random variable x is uniformly distributed on the interval [35, 45].
The probability that x is between 40 and 50 will be:
(45 - 40)/(45 - 35)
= 5/10
= 0.5
Learn more about probability on:
brainly.com/question/24756209
#SPJ4
Find the slope of the line passing through the points (-6, -5) and (4,4).
Answers
Answer:
9/10 or 0.9
Step-by-step explanation:
Slope of a line passing through two points (x1, y1) and (x2, y2) is given by
Slope m = rise/run
where
rise = y2 - y1
run = x2 - x1
Given points (- 6, - 5) and (4, 4),
rise = 4 - (-5) = 4 + 5 = 9
run = 4 - ( - 6) = 4 + 6 = 10
Slope = rise/run = 9/10 or 0.9
